人教版数学七下第2讲平行线的构造学案
图片预览


文档简介
第2讲 平行线的构造
课堂思维碰撞
第一层:平行线的基本模型
知识导入
基本几何模型:平行线+拐点
(1)单拐点锯齿模型(“猪蹄”模型)
已知:
结论:
(2)单拐点铅笔模型
已知:
结论:
(3)拐点在平行线外的模型
已知:
结论:
已知:
结论:
夯实基础
例1
(1)如图,,且,,则的度数是( )
A. B. C. D.
【答案】B
(2)如图,已知直线,,,则等于( )
A. B. C. D.
【答案】A
(3)如图,已知,则等于( )
A. B. C. D.
【答案】C
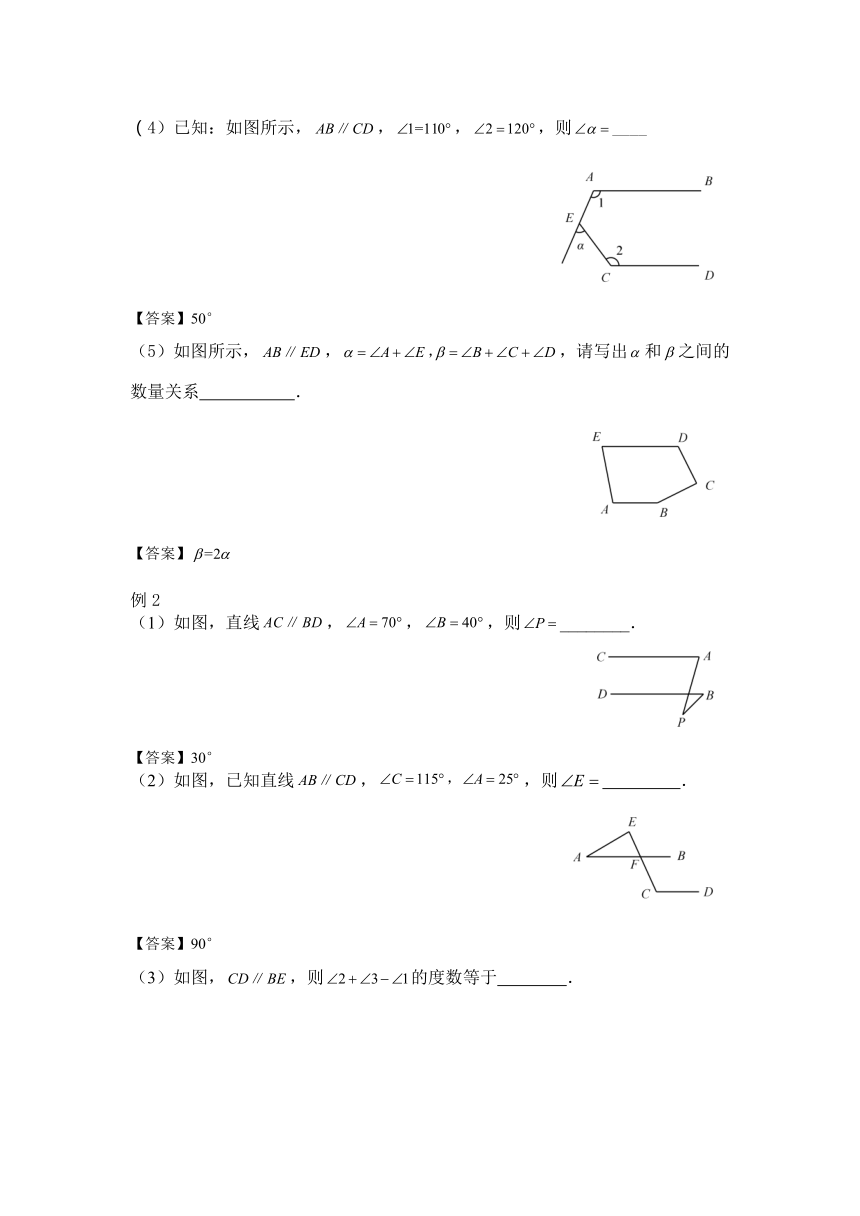
(4)已知:如图所示,,,,则____
【答案】50°
(5)如图所示,,,请写出和之间的数量关系 .
【答案】
例2
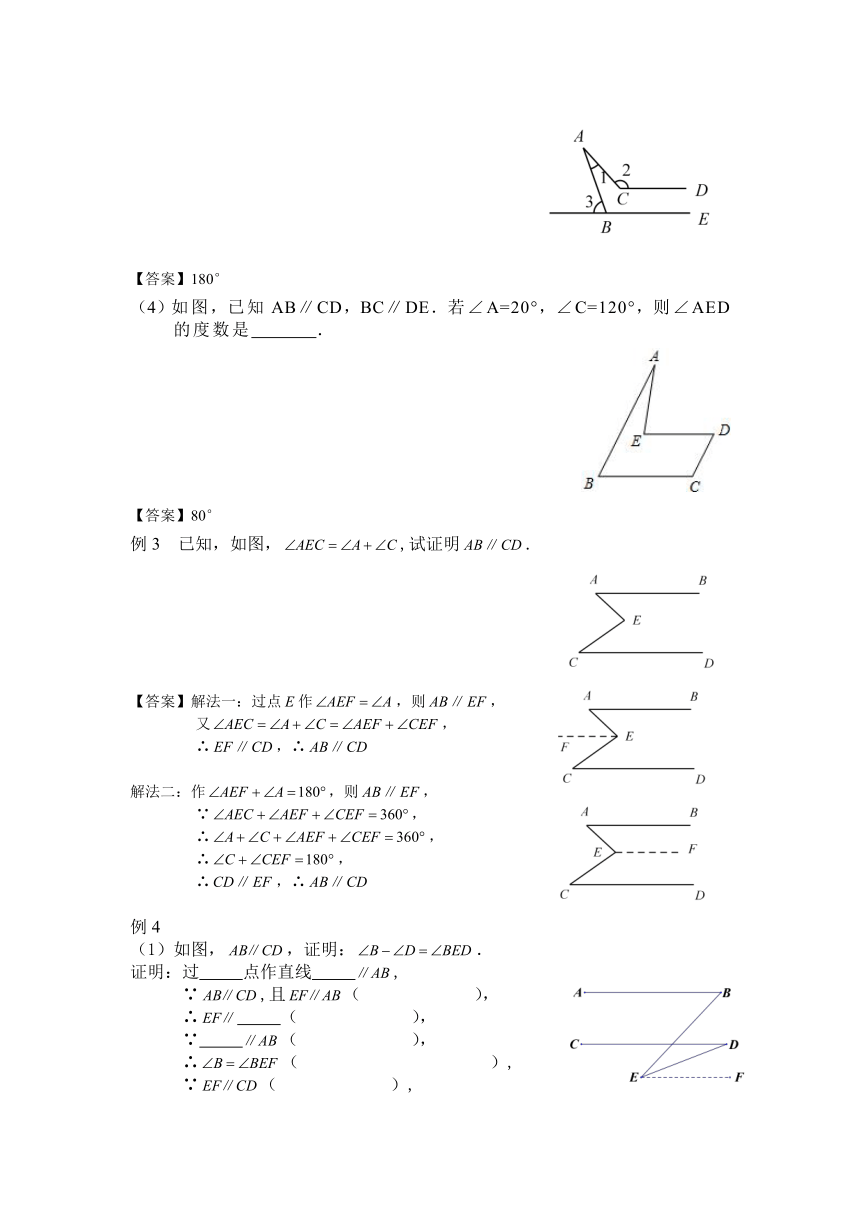
(1)如图,直线,,,则________.
【答案】30°
(2)如图,已知直线,,则 .
【答案】90°
(3)如图,,则的度数等于 .
【答案】180°
(4)如图,已知AB∥CD,BC∥DE.若∠A=20°,∠C=120°,则∠AED的度数是 .
【答案】80°
例3 已知,如图,,试证明.
【答案】解法一:过点作,则,
又,
∴,∴
解法二:作,则,
∵,
∴,
∴,
∴,∴
例4
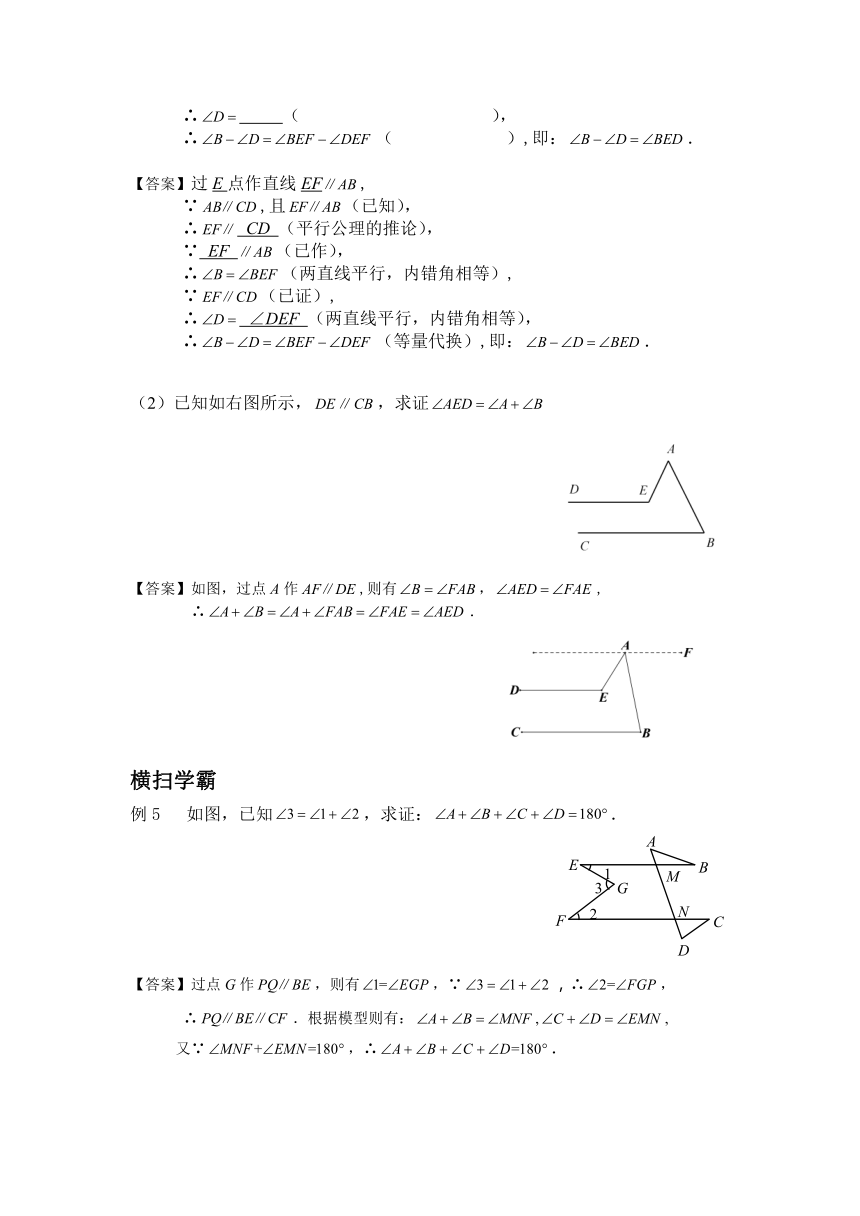
(1)如图,,证明:.
证明:过 点作直线 ,
∵,且( ),
∴ ( ),
∵ ( ),
∴( ),
∵( ),
∴ ( ),
∴( ),即:.
【答案】过E点作直线EF,
∵,且(已知),
∴ CD (平行公理的推论),
∵ EF (已作),
∴(两直线平行,内错角相等),
∵(已证),
∴ ∠DEF (两直线平行,内错角相等),
∴(等量代换),即:.
(2)已知如右图所示,,求证
【答案】如图,过点A作,则有,,
∴.
横扫学霸
例5 如图,已知,求证:.
【答案】过点G作,则有,∵,∴,
∴.根据模型则有:,,
又∵,∴.
第二层:多拐点图形中的平行线构造
1.辅助线:当从已知条件无法直接得出结论时,可以在图中添出新的线,为几何图形性质的应用创造条件,这些添置的线叫辅助线. 辅助线起着沟通已知和未知、化分散为集中等作用.
2.复杂的多拐点平行问题
(1)多拐点锯齿模型(已知:)
结论:
(2)多拐点铅笔模型(已知:)
结论:
3.利用平行线性质直接计算角度
利用平行线性质与判定综合的角度计算
能力提升
例6
(1)如图,AB//CD,则∠AEF+∠EFG+∠FGH+∠GHC = .
【答案】540°
(2)如图所示,两直线、平行,则_____ __.
【答案】900°
(3)如图,、、、、、、之间的关系是 .
【答案】
例7 (1)如图,已知,试说明.
【答案】如图,分别过点作的平行线,可证.
(2)如图,AB∥CD,∠E=60°,求的值.
【答案】如图,分别过点作的平行线,.
横扫学霸
例8 如图(1),已知,探索、、…、和、、…、之间的关系,并证明你的结论.
(2)如图(2),已知,探索、、、与、之间的关系,并证明你的结论.
(3)如图(3),已知,探索、、…、之间的关系,并证明你的结论.
【答案】(1);
(向右凸出的角的和=向左凸出的角的和,,均为锐角)
(2);注意和第⑴问的区别;
(3)
课后创新培养
课后作业
练1 (1)如图,已知直线AB∥CD,∠A=22°,∠C=40°,则∠E= .
【答案】62°
(2)如图,、、、之间的关系是 .
【答案】
练2 如图所示,已知AB∥CD,∠C=75°,∠A=25°,求∠E的度数.
【答案】50°.
练3 (1)如图,若,判断是否成立,并证明.反之,若,可否得直线AB与CD平行?请说明.
【答案】成立,过E点作的平行线即可证明.
(2)若点E移到如图位置,已知,试判断、、之间的关系,并说明理由.
【答案】,过E点作的平行线即可证明.
练4 如图所示,,求证.
【答案】过作,如下图所示,则有,
∴,∴,
∴.
练5 已知AB∥CD,∠1=30°,∠2=50°,∠3=60°,求∠4的度数.
【答案】140°.
课堂思维碰撞
第一层:平行线的基本模型
知识导入
基本几何模型:平行线+拐点
(1)单拐点锯齿模型(“猪蹄”模型)
已知:
结论:
(2)单拐点铅笔模型
已知:
结论:
(3)拐点在平行线外的模型
已知:
结论:
已知:
结论:
夯实基础
例1
(1)如图,,且,,则的度数是( )
A. B. C. D.
【答案】B
(2)如图,已知直线,,,则等于( )
A. B. C. D.
【答案】A
(3)如图,已知,则等于( )
A. B. C. D.
【答案】C
(4)已知:如图所示,,,,则____
【答案】50°
(5)如图所示,,,请写出和之间的数量关系 .
【答案】
例2
(1)如图,直线,,,则________.
【答案】30°
(2)如图,已知直线,,则 .
【答案】90°
(3)如图,,则的度数等于 .
【答案】180°
(4)如图,已知AB∥CD,BC∥DE.若∠A=20°,∠C=120°,则∠AED的度数是 .
【答案】80°
例3 已知,如图,,试证明.
【答案】解法一:过点作,则,
又,
∴,∴
解法二:作,则,
∵,
∴,
∴,
∴,∴
例4
(1)如图,,证明:.
证明:过 点作直线 ,
∵,且( ),
∴ ( ),
∵ ( ),
∴( ),
∵( ),
∴ ( ),
∴( ),即:.
【答案】过E点作直线EF,
∵,且(已知),
∴ CD (平行公理的推论),
∵ EF (已作),
∴(两直线平行,内错角相等),
∵(已证),
∴ ∠DEF (两直线平行,内错角相等),
∴(等量代换),即:.
(2)已知如右图所示,,求证
【答案】如图,过点A作,则有,,
∴.
横扫学霸
例5 如图,已知,求证:.
【答案】过点G作,则有,∵,∴,
∴.根据模型则有:,,
又∵,∴.
第二层:多拐点图形中的平行线构造
1.辅助线:当从已知条件无法直接得出结论时,可以在图中添出新的线,为几何图形性质的应用创造条件,这些添置的线叫辅助线. 辅助线起着沟通已知和未知、化分散为集中等作用.
2.复杂的多拐点平行问题
(1)多拐点锯齿模型(已知:)
结论:
(2)多拐点铅笔模型(已知:)
结论:
3.利用平行线性质直接计算角度
利用平行线性质与判定综合的角度计算
能力提升
例6
(1)如图,AB//CD,则∠AEF+∠EFG+∠FGH+∠GHC = .
【答案】540°
(2)如图所示,两直线、平行,则_____ __.
【答案】900°
(3)如图,、、、、、、之间的关系是 .
【答案】
例7 (1)如图,已知,试说明.
【答案】如图,分别过点作的平行线,可证.
(2)如图,AB∥CD,∠E=60°,求的值.
【答案】如图,分别过点作的平行线,.
横扫学霸
例8 如图(1),已知,探索、、…、和、、…、之间的关系,并证明你的结论.
(2)如图(2),已知,探索、、、与、之间的关系,并证明你的结论.
(3)如图(3),已知,探索、、…、之间的关系,并证明你的结论.
【答案】(1);
(向右凸出的角的和=向左凸出的角的和,,均为锐角)
(2);注意和第⑴问的区别;
(3)
课后创新培养
课后作业
练1 (1)如图,已知直线AB∥CD,∠A=22°,∠C=40°,则∠E= .
【答案】62°
(2)如图,、、、之间的关系是 .
【答案】
练2 如图所示,已知AB∥CD,∠C=75°,∠A=25°,求∠E的度数.
【答案】50°.
练3 (1)如图,若,判断是否成立,并证明.反之,若,可否得直线AB与CD平行?请说明.
【答案】成立,过E点作的平行线即可证明.
(2)若点E移到如图位置,已知,试判断、、之间的关系,并说明理由.
【答案】,过E点作的平行线即可证明.
练4 如图所示,,求证.
【答案】过作,如下图所示,则有,
∴,∴,
∴.
练5 已知AB∥CD,∠1=30°,∠2=50°,∠3=60°,求∠4的度数.
【答案】140°.
