2021-2022学年人教版数学九年级上册 24.4弧长及扇形面积 课件(共25张PPT)
文档属性
| 名称 | 2021-2022学年人教版数学九年级上册 24.4弧长及扇形面积 课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 673.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-25 11:25:19 | ||
图片预览





文档简介
(共25张PPT)
24.4 弧长和扇形面积
学习目标:
1、理解弧长和面积公式。
2、能熟练运用弧长和面积公式计算。
弧
半径
半径
A
A
B
B
O
O
“扇子”与“扇形”、“弧”
弧
半径
半径
扇形
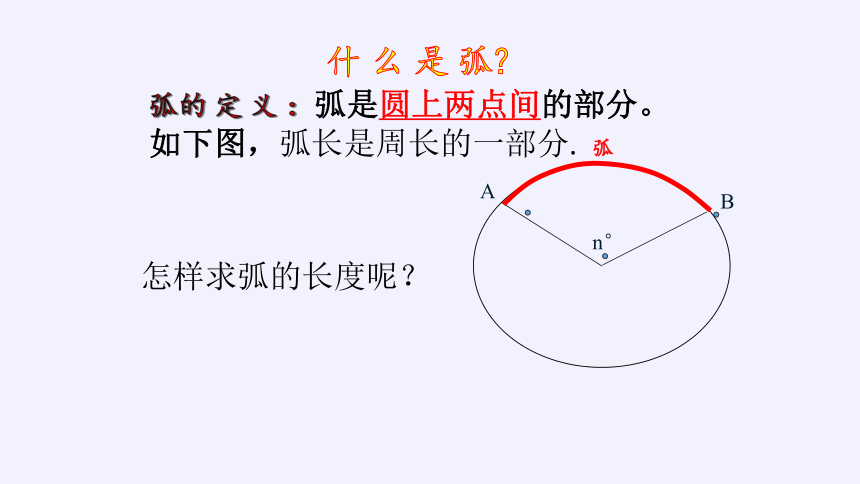
弧的 定 义 :弧是圆上两点间的部分。如下图,弧长是周长的一部分.
什 么 是 弧?
n°
A
B
怎样求弧的长度呢?
弧
(1)半径为R的圆,周长是多少?
?
C=2πR
点燃思维的火花
n°
o
(3) n0的圆心角所对的弧长是整
个圆周的几分之几?
R
(2) 1°圆心角所对的弧长是整个圆周的几分之几?
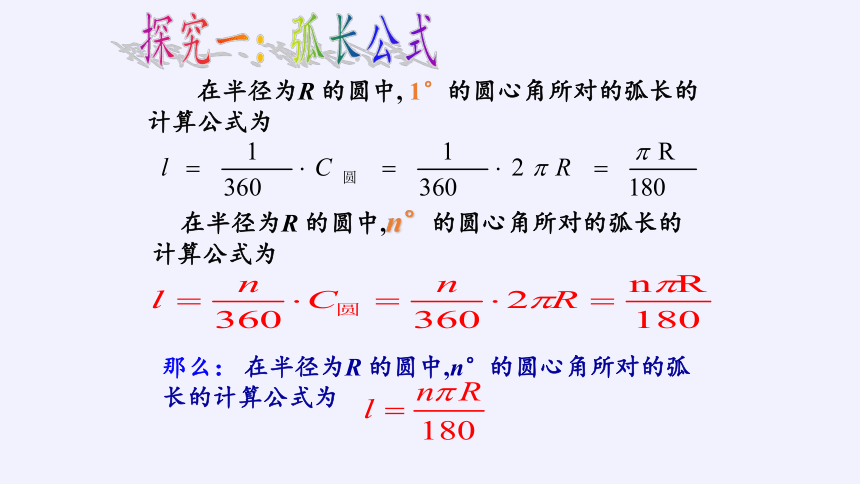
在半径为R 的圆中,n°的圆心角所对的弧长的计算公式为
在半径为R 的圆中, 1°的圆心角所对的弧长的计算公式为
探究一:弧长公式
那么: 在半径为R 的圆中,n°的圆心角所对的弧长的计算公式为
试一试
1.已知弧所对的圆心角为900,半径是4,则弧
长为 ;
2.已知一条弧的半径为9,弧长为8 ,那么这
条弧所对的圆心角为 ;
1600
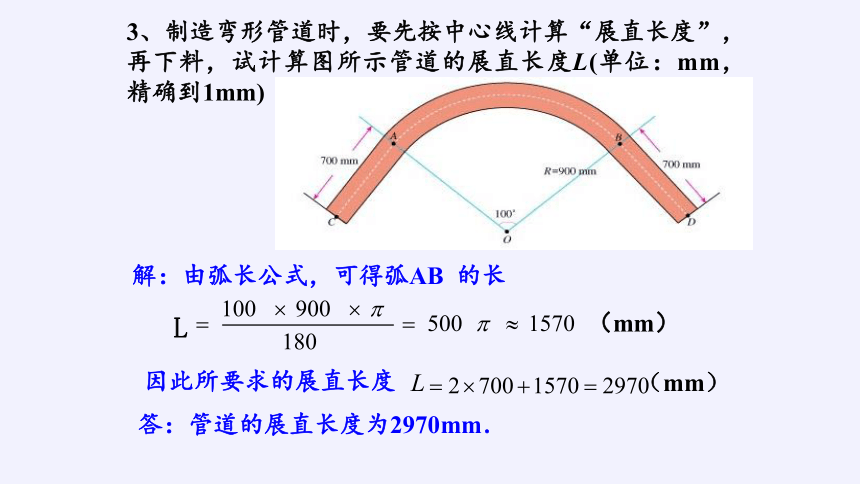
3、制造弯形管道时,要先按中心线计算“展直长度”,再下料,试计算图所示管道的展直长度L(单位:mm,精确到1mm)
解:由弧长公式,可得弧AB 的长
L
因此所要求的展直长度
L (mm)
答:管道的展直长度为2970mm.
(mm)
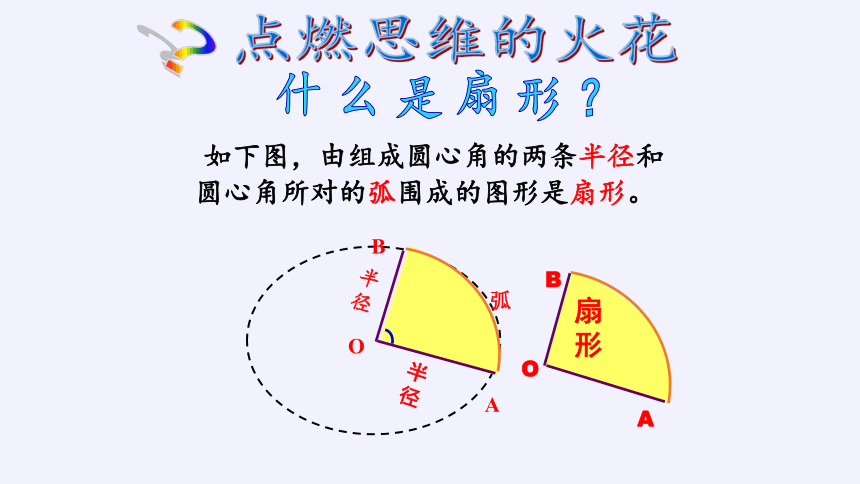
什 么 是 扇 形 ?
如下图,由组成圆心角的两条半径和圆心角所对的弧围成的图形是扇形。
半径
O
B
A
弧
O
B
A
扇形
点燃思维的火花
?
半径
2、圆心角为n°的扇形是整个圆的
几分之几
1、半径为R的圆,面积是多少?
那么: 在半径为R 的圆中,n°的圆心角所对的扇形面积的计算公式为
如果圆的半径为R,则圆的面积为 ,
l°的圆心角对应的扇形面积为 ,
°的圆心角对应的扇形面积为
1、已知扇形的圆心角为120°,半径为2,
则这个扇形的面积S扇形=_ .
2、已知扇形面积为 ,圆心角为60°,
则这个扇形的半径R=____.
做一做
如图、水平放置的圆柱形排水管道的截面半径是0.6m,其中水面高0.3m,求截面上有水部分的面积。(精确到0.01m)。
分析:有水部分的
面积= S扇- S△
综合应用
生活中的数学
0
B
A
C
D
0
变式升华
14
S弓形=S扇形- S三角形
S弓形=S扇形+ S三角形
0
0
弓形的面积是扇形的面积与三角形
面积的和或差
规律提升
想一想:扇形的面积公式与什么公式类似?
探究三:弧长公式和扇形面积的关系
1、已知半径为2cm的扇形,其弧长为 ,
则这个扇形的面积S扇形=——.
做一做
2、已知半径为4的扇形,面积为 ,则这个
扇形的弧长=____.
1、已知扇形的圆心角为120°,半径为2,则这个扇形的面积为____.
2、已知扇形的圆心角为30°,面积为 3πc㎡, 则这个扇形的半径R=____.
3、如图,有一段弯道是圆弧形的,弯道长12m,弧所对的圆心角是81°,求这段圆弧所在圆的半径R是多少m?
当堂测验
6cm
12m
81°
R
决胜中考——中考题回顾
1.如图,⊙A、 ⊙B、 ⊙C、 ⊙D两两不相交,且半径都是2cm,求图中阴影部分的面积 cm2 .
2.如图,两个同心圆中,大圆的
半OA=4cm,∠AOB=∠BOC=60°则图中阴影部分的面积是_____cm2。
12π
3.如图所示,分别以n边形的顶点为圆心,以单位1为半径画圆,则图中阴影部分的面积之和为 个平方单位.
决胜中考——中考题回顾
1、已知扇形的半径为3cm,所对的圆心角为80°,则弧长为______________,面积为___________.
2、已知扇形的圆心角为60 °,弧长为10πcm,则扇形的半径为__________,面积为___________.
3、已知扇形的半径为6cm,面积为12πcm2,则扇形的圆心角为________,弧长为___________.
课后练习
4、已知扇形的圆心角为90°,半径为2,则这个扇形的面积S扇形= ____.
练习
5、已知扇形面积为 ,圆心角为60°,则这个扇形的半径R=____.
6.如图,半径为5的半圆的初始状态是直径平行于桌面上的直线b,然后把半圆沿直线b进行无滑动滚动,使半圆的直径与直线b重合为止,则圆心O运动路径的长度等于___.
7. 已知等边三角形ABC的边长为a,分别以A、B、C为圆心,以 为半径的圆相切于点D、 E、F,求图中阴影部分的面积S.
8.如图,Rt△ABC中,∠C=90°,∠A=30°,AB=4,将△ABC绕 点B按顺时针方向转动一个角到△A′BC′的位置,使点A、B、C′在同一条直线上,求图中阴影部分的面积.
归纳 小结
请你说给大家听听
这节课你有那些收获
谢 谢
24.4 弧长和扇形面积
学习目标:
1、理解弧长和面积公式。
2、能熟练运用弧长和面积公式计算。
弧
半径
半径
A
A
B
B
O
O
“扇子”与“扇形”、“弧”
弧
半径
半径
扇形
弧的 定 义 :弧是圆上两点间的部分。如下图,弧长是周长的一部分.
什 么 是 弧?
n°
A
B
怎样求弧的长度呢?
弧
(1)半径为R的圆,周长是多少?
?
C=2πR
点燃思维的火花
n°
o
(3) n0的圆心角所对的弧长是整
个圆周的几分之几?
R
(2) 1°圆心角所对的弧长是整个圆周的几分之几?
在半径为R 的圆中,n°的圆心角所对的弧长的计算公式为
在半径为R 的圆中, 1°的圆心角所对的弧长的计算公式为
探究一:弧长公式
那么: 在半径为R 的圆中,n°的圆心角所对的弧长的计算公式为
试一试
1.已知弧所对的圆心角为900,半径是4,则弧
长为 ;
2.已知一条弧的半径为9,弧长为8 ,那么这
条弧所对的圆心角为 ;
1600
3、制造弯形管道时,要先按中心线计算“展直长度”,再下料,试计算图所示管道的展直长度L(单位:mm,精确到1mm)
解:由弧长公式,可得弧AB 的长
L
因此所要求的展直长度
L (mm)
答:管道的展直长度为2970mm.
(mm)
什 么 是 扇 形 ?
如下图,由组成圆心角的两条半径和圆心角所对的弧围成的图形是扇形。
半径
O
B
A
弧
O
B
A
扇形
点燃思维的火花
?
半径
2、圆心角为n°的扇形是整个圆的
几分之几
1、半径为R的圆,面积是多少?
那么: 在半径为R 的圆中,n°的圆心角所对的扇形面积的计算公式为
如果圆的半径为R,则圆的面积为 ,
l°的圆心角对应的扇形面积为 ,
°的圆心角对应的扇形面积为
1、已知扇形的圆心角为120°,半径为2,
则这个扇形的面积S扇形=_ .
2、已知扇形面积为 ,圆心角为60°,
则这个扇形的半径R=____.
做一做
如图、水平放置的圆柱形排水管道的截面半径是0.6m,其中水面高0.3m,求截面上有水部分的面积。(精确到0.01m)。
分析:有水部分的
面积= S扇- S△
综合应用
生活中的数学
0
B
A
C
D
0
变式升华
14
S弓形=S扇形- S三角形
S弓形=S扇形+ S三角形
0
0
弓形的面积是扇形的面积与三角形
面积的和或差
规律提升
想一想:扇形的面积公式与什么公式类似?
探究三:弧长公式和扇形面积的关系
1、已知半径为2cm的扇形,其弧长为 ,
则这个扇形的面积S扇形=——.
做一做
2、已知半径为4的扇形,面积为 ,则这个
扇形的弧长=____.
1、已知扇形的圆心角为120°,半径为2,则这个扇形的面积为____.
2、已知扇形的圆心角为30°,面积为 3πc㎡, 则这个扇形的半径R=____.
3、如图,有一段弯道是圆弧形的,弯道长12m,弧所对的圆心角是81°,求这段圆弧所在圆的半径R是多少m?
当堂测验
6cm
12m
81°
R
决胜中考——中考题回顾
1.如图,⊙A、 ⊙B、 ⊙C、 ⊙D两两不相交,且半径都是2cm,求图中阴影部分的面积 cm2 .
2.如图,两个同心圆中,大圆的
半OA=4cm,∠AOB=∠BOC=60°则图中阴影部分的面积是_____cm2。
12π
3.如图所示,分别以n边形的顶点为圆心,以单位1为半径画圆,则图中阴影部分的面积之和为 个平方单位.
决胜中考——中考题回顾
1、已知扇形的半径为3cm,所对的圆心角为80°,则弧长为______________,面积为___________.
2、已知扇形的圆心角为60 °,弧长为10πcm,则扇形的半径为__________,面积为___________.
3、已知扇形的半径为6cm,面积为12πcm2,则扇形的圆心角为________,弧长为___________.
课后练习
4、已知扇形的圆心角为90°,半径为2,则这个扇形的面积S扇形= ____.
练习
5、已知扇形面积为 ,圆心角为60°,则这个扇形的半径R=____.
6.如图,半径为5的半圆的初始状态是直径平行于桌面上的直线b,然后把半圆沿直线b进行无滑动滚动,使半圆的直径与直线b重合为止,则圆心O运动路径的长度等于___.
7. 已知等边三角形ABC的边长为a,分别以A、B、C为圆心,以 为半径的圆相切于点D、 E、F,求图中阴影部分的面积S.
8.如图,Rt△ABC中,∠C=90°,∠A=30°,AB=4,将△ABC绕 点B按顺时针方向转动一个角到△A′BC′的位置,使点A、B、C′在同一条直线上,求图中阴影部分的面积.
归纳 小结
请你说给大家听听
这节课你有那些收获
谢 谢
同课章节目录
