2021-2022学年人教版(五四制)六年级上学期数学期末练习试卷(word版含答案)
文档属性
| 名称 | 2021-2022学年人教版(五四制)六年级上学期数学期末练习试卷(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 264.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-26 11:27:20 | ||
图片预览




文档简介
2021-2022学年人教五四新版六年级上学期数学期末练习试卷一.选择题(共10小题,满分30分,每小题3分)
1.﹣2021的倒数为( )
A. B. C.﹣2021 D.2021
2.下列四个图形中,其中不是轴对称图形的是( )
A. B. C. D.
3.已知a、b为有理数,下列式子:①|ab|>ab;②;③;④a3+b3=0.其中一定能够表示a、b异号的有( )个.
A.1 B.2 C.3 D.4
4.计算18÷(﹣3)的结果等于( )
A.﹣6 B.6 C.﹣15 D.15
5.如图,数轴上A、B、C三点所表示的数分别为a、b、c,满足a+b﹣c=0且AB=BC.那么下列各式正确的是( )
A.a+c<0 B.ac>0 C.bc<0 D.ab<0
6.若扇形的半径为3,圆心角为60°,则此扇形的弧长是( )
A.π B.π C.π D.2π
7.A、B两地的实际距离AB=250米,如果画在地图上的距离A′B′=5厘米,那么地图上的距离与实际距离的比为( )
A.1:500 B.1:5000 C.500:1 D.5000:1
8.某市为提倡节约用水,采取分段收费.若每户每月用水不超过10吨,每吨收费4元;若超过10吨,超过部分每吨加收1元.小明家5月份交水费60元,则他家该月用水( )
A.12吨 B.14吨 C.15吨 D.16吨
9.定义a※b=a2÷(b﹣1),例如3※5=32÷(5﹣1)=9÷4=,则(﹣3)※4的结果为( )
A.﹣3 B.3 C. D.
10.如图,点P为∠AOB内一点,分别作出P点关于OB、OA的对称点P1,P2,连接P1P2交OB于M,交OA于N,若∠AOB=40°,则∠MPN的度数是( )
A.90° B.100° C.120° D.140°
二.填空题(共10小题,满分30分,每小题3分)
11.在数,﹣0.4,0. 2,3.14,0.1010010001…(每两个之间多一个0),120%,,100这8个数中,有理数有 个.
12.如图,以第一个圆的半径为直径画出第二个圆,再以第二个圆的半径为直径画出第三个圆,第三个圆与第一个圆的面积之比为 .
13.某品牌汽车公司大力推进技术革新,新款汽车油耗从每百公里8升下降到每百公里6.8升,那么该汽车油耗的下降率为 .
14.一个圆的周长是12.56米,它的面积是 (π取3.14).
15.计算:3×(﹣)= .
16.如图,将正整数按此规律排列成数表,则2021是表中第 行第 列.
17.把四张形状大小完全相同的小长方形卡片(如图1)按两种不同的方式,不重叠地放在一个底面为长方形(一边长为4)的盒子底部(如图2、图3),盒子底面未被卡片覆盖的部分用阴影表示.已知阴影部分均为长方形,且图2与图3阴影部分周长之比为5:6,则盒子底部长方形的面积为 .
18.计算(﹣9)÷×的结果是 .
19.南山植物园坐落在省级南山风景名胜区群山之中,与重庆主城区夹长江面峙,是一个以森林为基础,花卉为特色的综合性公园.备受重庆人民的喜爱;每到春季,上山赏花的人络绎不绝;一植物园附近的市民嗅到了商机,开办了植物花卉门市;将A、B、C三种花卉包装成“如沐春风”、“懵懂少女”、“粉色回忆”三种不同的礼盒进行销售;用A花卉2支、B花卉4支、C花卉10支包装成“如沐春风”礼盒;用A花卉2支、B花卉2支、C种花卉4支包装成“惜懂少女”礼盒;用A花卉2支、B花卉3支、C花卉6支包装成“粉色回忆”礼盒;包装费忽略不计,且每支B花卉的成本是每支C花卉成本的4倍,每盒“如沐春风”礼盒的总成本是每盒“懵懂少女”礼盒总成本的2倍;该商家将三种礼盒均以利润率50%进行定价销售;某周末,该门市为了加大销量,将“如沐春风”、“懵懂少女”两种礼盒打八折进行销售,且两种礼盒的销量相同,“粉色回忆”礼盒打九折销售;销售完毕后统计发现,三种礼盒的总成本恰好为总利润的4倍,则该周末“粉色回忆”礼盒的总利润与三种礼盒的总利润的比值为 .
20.某同学在数学实践活动中,制作了一个侧面积为60π,底面半径为6的圆锥模型(如图所示),则此圆锥的母线长为 .
三.解答题(共7小题,满分60分)
21.(8分)计算:
(1)16÷(﹣2)3﹣(﹣)×(﹣4)+(﹣1)2020;
(2)﹣14﹣(1﹣0.5)××[2﹣(﹣3)2].
22.(8分)解方程
(1)x:4=6:2;
(2)48÷﹣0.4x=4;
(3)3x﹣1.2x=36.
23.(8分)按3:1的比画出三角形放大后的图形;按1:2的比画出长方形缩小后的图形.
24.(8分)我们可以用“肥胖百分数”来表示一个人的胖瘦情况,“肥胖百分数”是用体重(千克)除以身高(分米)的平方.再乘以100%,即肥胖百分数=×100%,一般认为:肥胖百分数在18%~20%的人偏瘦,在20%~24%的人为基本正常,在24%~26%的人偏胖.
(1)小明的父亲身高180厘米,体重80千克,试判断小明父亲的胖瘦情况
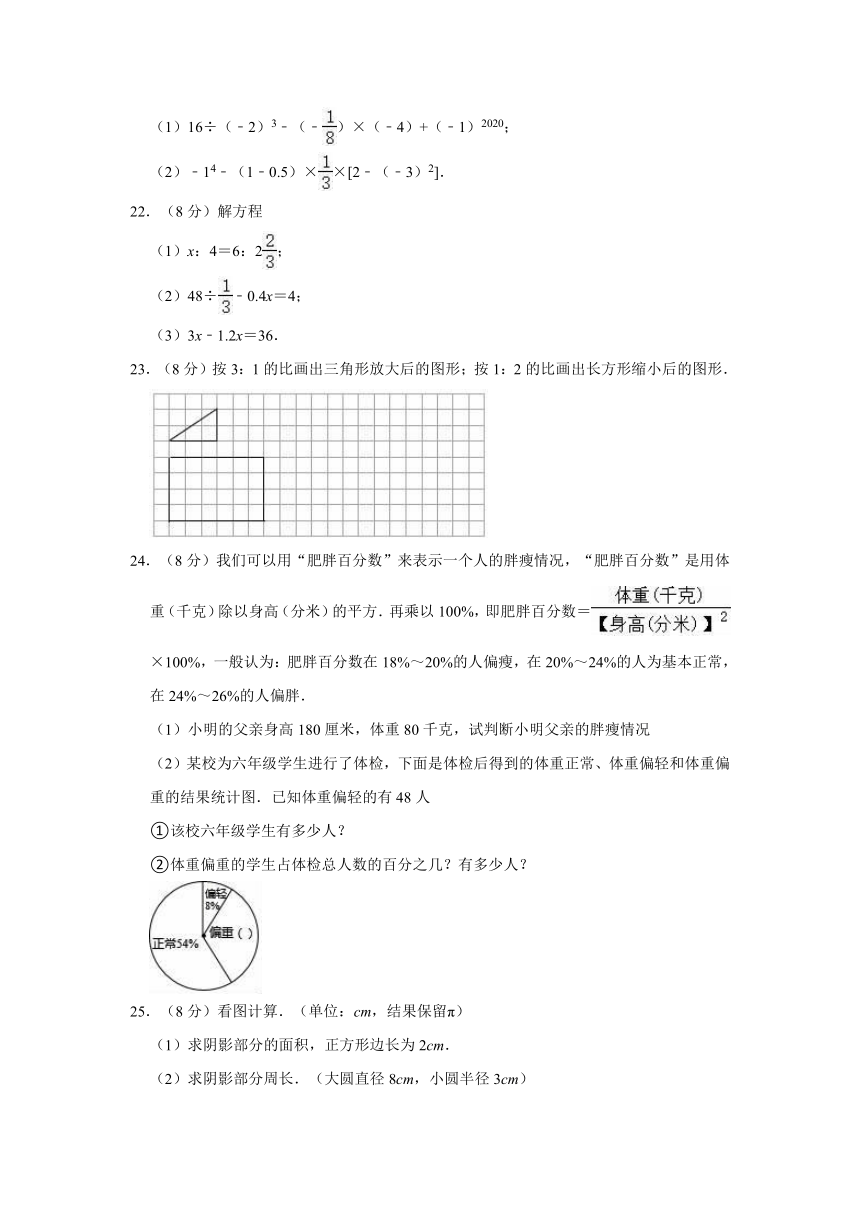
(2)某校为六年级学生进行了体检,下面是体检后得到的体重正常、体重偏轻和体重偏重的结果统计图.已知体重偏轻的有48人
①该校六年级学生有多少人?
②体重偏重的学生占体检总人数的百分之几?有多少人?
25.(8分)看图计算.(单位:cm,结果保留π)
(1)求阴影部分的面积,正方形边长为2cm.
(2)求阴影部分周长.(大圆直径8cm,小圆半径3cm)
26.(10分)列方程解应用题:如图,现有两条乡村公路AB、BC,AB长为1200米,BC长为1600米,一个人骑摩托车从A处以20m/s的速度匀速沿公路AB、BC向C处行驶;另一人骑自行车从B处以5m/s的速度从B向C行驶,并且两人同时出发.
(1)求经过多少秒摩托车追上自行车?
(2)求两人均在行驶途中时,经过多少秒两人在行进路线上相距150米?
27.(10分)列方程解应用题:已知A,B两地相距60千米,甲骑自行车,乙骑摩托车都沿一条笔直的公路由A地匀速行驶到B地,乙每小时比甲多行30千米,甲比乙早出发3小时,乙出发1小时后刚好追上甲.
(1)求甲的速度;
(2)问乙出发之后,到达B地之前,何时甲乙两人相距6千米;
(3)若丙骑自行车与甲同时出发,沿着这条笔直的公路由B地匀速行驶到A地,经过小时与乙相遇,求此时甲、丙两人之间距离.
参考答案与试题解析
一.选择题(共10小题,满分30分,每小题3分)
1.解:﹣2021的倒数为:﹣.
故选:A.
2.解:选项A、C、D能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以是轴对称图形,
选项B不能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以不是轴对称图形,
故选:B.
3.解:当|ab|>ab时,a、b一定异号;
当<0时,a、b一定异号;
当||=﹣,则≤0,a可能等于0,b≠0,a、b不一定异号;
当a3+b3=0,a3=﹣b3,即a3=(﹣b)3,
所以a=﹣b,有可能a=b=0,a、b不一定异号.
所以一定能够表示a、b异号的有①②.
故选:B.
4.解:18÷(﹣3)
=﹣(18÷3)
=﹣6.
故选:A.
5.解:∵AB=BC,
∴b﹣a=c﹣b,
∴a+c=2b,
∵a+b﹣c=0,即c=a+b,
∴a+(a+b)=2b,
∴b=2a,
∴c=a+b=3a,
∵a<b<c,
∴a>0,b>0,c>0,
∴a+c>0,则A选项错误;
ac>0,则B选项正确;
bc>0,则C错误;
ab>0,则D错误.
故选:B.
6.解:∵一个扇形的半径长为3,且圆心角为60°,
∴此扇形的弧长为=π.
故选:B.
7.解:取米作为共同的长度单位,那么AB=250米,A'B'=5厘米=0.05米,
所以==,
所以地图上的距离与实际距离的比为1:5000.
故选:B.
8.解:设他家该月用水x吨,
∵10×4=40<60,
∴10×4+(4+1)×(x﹣10)=60,
解得x=14,
答:他家该月用水14吨.
故选:B.
9.解:∵a※b=a2÷(b﹣1),
∴(﹣3)※4
=(﹣3)2÷(4﹣1)
=9÷3
=3,
故选:B.
10.解:∵P点关于OB的对称点是P1,P点关于OA的对称点是P2,
∴PM=P1M,PN=P2N,∠P2=∠P2PN,∠P1=∠P1PM,
∵∠AOB=40°,
∴∠P2PP1=140°,
∴∠P1+∠P2=40°,
∴∠PMN=∠P1+∠MPP1=2∠P1,∠PNM=∠P2+∠NPP2=2∠P2,
∴∠PMN+∠PNM=2×40°=80°,
∴∠MPN=180°﹣(∠PMN+∠PNM)=180°﹣80°=100°,
故选:B.
二.填空题(共10小题,满分30分,每小题3分)
11.解:在,﹣0.4,0. 2,3.14,0.1010010001…(每两个之间多一个0),120%,,100中,有理数有﹣0.4,0. 2,3.14,120%,,100等6个.
故答案为:6.
12.解:设第一个圆(大圆)的半径为r,
则第三个圆的半径为r=r,
∴第三个圆与第一个圆的面积之比为=,
故答案为:.
13.解:根据题意得,8﹣6.8=1.2(升),
1.2÷8=15%,
∴该汽车油耗下降率为15%.
故答案为:15%.
14.解:∵圆的周长是12.56米,
∴圆的半径为12.56÷2π=2米,
∴圆的面积为π×22=12.56(平方米),
故答案为:12.56平方米.
15.解:原式=﹣.
故答案为:.
16.解:由图可知,
第一行1个数字,
第二行2个数字,
第三行3个数字,
…,
则第n行n个数字,
前n行一共有个数字,
∵<2021<,2021﹣=2021﹣2016=5,
∴2021是表中第64行第5列,
故答案为:64,5.
17.解:设小长方形卡片的长为2m,则宽为m,
依题意,得:2m+2m=4,
解得:m=1,
∴2m=2.
再设盒子底部长方形的另一边长为x,
依题意,得:2(4+x﹣2):2×2(2+x﹣2)=5:6,
整理,得:10x=12+6x,
解得:x=3,
∴盒子底部长方形的面积=4×3=12.
故答案为:12.
18.解:(﹣9)÷×=(﹣9)××=﹣6×=﹣4,
故答案为:﹣4.
19.解:设C花卉一支x元,A花卉一支y元,则B花卉一支4x元,
∵每盒“如沐春风”礼盒的总成本是每盒“懵懂少女”礼盒总成本的2倍,
∴2y+4×4x+10x=2(2y+2×4x+4x),
化简整理得y=x,
∴A花卉一支x元,C花卉一支x元,B花卉一支4x元,
∴“如沐春风”礼盒每盒成本为2x+4×4x+10x=28x(元),以利润率50%定价为28x×(1+50%)=42x(元),打八折销售售价是42x×0.8=33.6x(元),
“懵懂少女”礼盒每盒成本为2x+2×4x+4x=14x(元),以利润率50%定价为14x×(1+50%)=21x(元),打八折销售售价是21x×0.8=16.8x(元),
“粉色回忆”礼盒每盒成本为2x+3×4x+6x=20x(元),以利润率50%定价为20x×(1+50%)=30x(元),打九折销售售价是30x×0.9=27x(元),
由某周末,该门市为了加大销量,将“如沐春风”、“懵懂少女”两种礼盒打八折进行销售,且两种礼盒的销量相同,设这两种礼盒都销售了a盒,粉色回忆”礼盒销售了b盒,根据三种礼盒的总成本恰好为总利润的4倍可得:
28x a+14x a+20x b=4[(33.6x﹣28x) a+(16.8x﹣14x) a+(27x﹣20x) b],
化简整理得:b=a,
∴该周末“粉色回忆”礼盒的总利润为(27x﹣20x) b=7x a=7.35xa,
该周末三种礼盒的总利润为(33.6x﹣28x) a+(16.8x﹣14x) a+(27x﹣20x) b=5.6xa+2.8xa+7.35xa=15.75xa,
∴该周末“粉色回忆”礼盒的总利润与三种礼盒的总利润的比值为=,
故答案为:.
20.解:设此圆锥的母线长为l,
根据题意得×2π×6×l=60π,解得l=10,
所以此圆锥的母线长为10.
故答案为10.
三.解答题(共7小题,满分60分)
21.解:(1)16÷(﹣2)3﹣(﹣)×(﹣4)+(﹣1)2020
=16÷(﹣8)﹣+1
=﹣2﹣+1
=﹣;
(2)﹣14﹣(1﹣0.5)××[2﹣(﹣3)2]
=﹣1﹣×(2﹣9)
=﹣1﹣×(﹣7)
=.
22.解:(1)x:4=6:2,
2x=24,
x=9;
(2)48÷﹣0.4x=4,
144﹣0.4x=4,
﹣0.4x=﹣140,
x=350;
(3)3x﹣1.2x=36,
1.8x=36,
x=20.
23.解:如图所示:
.
24.解:(1)×100%≈25%,
25%在24%~26%之间,属于偏胖的范围,
答:小明的父亲偏胖;
(2)①该校六年级学生有48÷8%=600(人);
②1﹣8%﹣54%=38%,
600×38%=228(人),
答:体重偏重的学生占体检总人数的38%,有228人.
25.解:(1)×2﹣2×2=(2π﹣4)cm2,
答:阴影部分的面积为(2π﹣4)cm2;
(2)×8π+×2π×3+4=(7π+4)cm,
答:阴影部分周长为(7π+4)cm.
26.解:(1)设经过x秒摩托车追上自行车,
20x=5x+1200,
解得x=80.
答:经过80秒摩托车追上自行车.
(2)(1200+1600)÷20=140(秒).
设经过y秒两人相距150米,
第一种情况:摩托车还差150米追上自行车时,
20y﹣1200=5y﹣150
解得y=70,符合题意.
第二种情况:摩托车超过自行车150米时,
20y=150+5y+1200
解得y=90,符合题意.
答:经过70秒或90秒两人在行进路线上相距150米.
27.解:(1)设甲速度为x千米/小时,则乙速度为(x+30)千米/小时
由题意可列方程:4x=x+30
解得:x=10
所以,甲速度为10千米/时;
(2)由(1)可知,甲速度为10千米/小时,乙速度为10+30=40千米/小时,
设乙出发后t小时甲乙相距6千米,则甲出发(t+3)小时,
相遇前:甲比乙多行驶6千米,可列方程10(t+3)﹣40t=6,
解得:t=0.8,
相遇后:乙比甲多行驶6千米,可列方程40t﹣10(t+3)=6,
解得t=1.2,
综上所述,乙出发0.8小时或1.2小时,甲乙相距6千米;
(3)设丙的速度为a千米/小时,丙与甲同时出发,所以丙行驶小时,乙行驶了﹣3=(小时).
根据题意可列方程a+×40=60,
解得:a=10,
所以丙的速度为10千米/小时,
经过小时,丙行驶×10=36(千米),甲行驶×10=36(千米),
所以两人相距36+36﹣60=12(千米).
1.﹣2021的倒数为( )
A. B. C.﹣2021 D.2021
2.下列四个图形中,其中不是轴对称图形的是( )
A. B. C. D.
3.已知a、b为有理数,下列式子:①|ab|>ab;②;③;④a3+b3=0.其中一定能够表示a、b异号的有( )个.
A.1 B.2 C.3 D.4
4.计算18÷(﹣3)的结果等于( )
A.﹣6 B.6 C.﹣15 D.15
5.如图,数轴上A、B、C三点所表示的数分别为a、b、c,满足a+b﹣c=0且AB=BC.那么下列各式正确的是( )
A.a+c<0 B.ac>0 C.bc<0 D.ab<0
6.若扇形的半径为3,圆心角为60°,则此扇形的弧长是( )
A.π B.π C.π D.2π
7.A、B两地的实际距离AB=250米,如果画在地图上的距离A′B′=5厘米,那么地图上的距离与实际距离的比为( )
A.1:500 B.1:5000 C.500:1 D.5000:1
8.某市为提倡节约用水,采取分段收费.若每户每月用水不超过10吨,每吨收费4元;若超过10吨,超过部分每吨加收1元.小明家5月份交水费60元,则他家该月用水( )
A.12吨 B.14吨 C.15吨 D.16吨
9.定义a※b=a2÷(b﹣1),例如3※5=32÷(5﹣1)=9÷4=,则(﹣3)※4的结果为( )
A.﹣3 B.3 C. D.
10.如图,点P为∠AOB内一点,分别作出P点关于OB、OA的对称点P1,P2,连接P1P2交OB于M,交OA于N,若∠AOB=40°,则∠MPN的度数是( )
A.90° B.100° C.120° D.140°
二.填空题(共10小题,满分30分,每小题3分)
11.在数,﹣0.4,0. 2,3.14,0.1010010001…(每两个之间多一个0),120%,,100这8个数中,有理数有 个.
12.如图,以第一个圆的半径为直径画出第二个圆,再以第二个圆的半径为直径画出第三个圆,第三个圆与第一个圆的面积之比为 .
13.某品牌汽车公司大力推进技术革新,新款汽车油耗从每百公里8升下降到每百公里6.8升,那么该汽车油耗的下降率为 .
14.一个圆的周长是12.56米,它的面积是 (π取3.14).
15.计算:3×(﹣)= .
16.如图,将正整数按此规律排列成数表,则2021是表中第 行第 列.
17.把四张形状大小完全相同的小长方形卡片(如图1)按两种不同的方式,不重叠地放在一个底面为长方形(一边长为4)的盒子底部(如图2、图3),盒子底面未被卡片覆盖的部分用阴影表示.已知阴影部分均为长方形,且图2与图3阴影部分周长之比为5:6,则盒子底部长方形的面积为 .
18.计算(﹣9)÷×的结果是 .
19.南山植物园坐落在省级南山风景名胜区群山之中,与重庆主城区夹长江面峙,是一个以森林为基础,花卉为特色的综合性公园.备受重庆人民的喜爱;每到春季,上山赏花的人络绎不绝;一植物园附近的市民嗅到了商机,开办了植物花卉门市;将A、B、C三种花卉包装成“如沐春风”、“懵懂少女”、“粉色回忆”三种不同的礼盒进行销售;用A花卉2支、B花卉4支、C花卉10支包装成“如沐春风”礼盒;用A花卉2支、B花卉2支、C种花卉4支包装成“惜懂少女”礼盒;用A花卉2支、B花卉3支、C花卉6支包装成“粉色回忆”礼盒;包装费忽略不计,且每支B花卉的成本是每支C花卉成本的4倍,每盒“如沐春风”礼盒的总成本是每盒“懵懂少女”礼盒总成本的2倍;该商家将三种礼盒均以利润率50%进行定价销售;某周末,该门市为了加大销量,将“如沐春风”、“懵懂少女”两种礼盒打八折进行销售,且两种礼盒的销量相同,“粉色回忆”礼盒打九折销售;销售完毕后统计发现,三种礼盒的总成本恰好为总利润的4倍,则该周末“粉色回忆”礼盒的总利润与三种礼盒的总利润的比值为 .
20.某同学在数学实践活动中,制作了一个侧面积为60π,底面半径为6的圆锥模型(如图所示),则此圆锥的母线长为 .
三.解答题(共7小题,满分60分)
21.(8分)计算:
(1)16÷(﹣2)3﹣(﹣)×(﹣4)+(﹣1)2020;
(2)﹣14﹣(1﹣0.5)××[2﹣(﹣3)2].
22.(8分)解方程
(1)x:4=6:2;
(2)48÷﹣0.4x=4;
(3)3x﹣1.2x=36.
23.(8分)按3:1的比画出三角形放大后的图形;按1:2的比画出长方形缩小后的图形.
24.(8分)我们可以用“肥胖百分数”来表示一个人的胖瘦情况,“肥胖百分数”是用体重(千克)除以身高(分米)的平方.再乘以100%,即肥胖百分数=×100%,一般认为:肥胖百分数在18%~20%的人偏瘦,在20%~24%的人为基本正常,在24%~26%的人偏胖.
(1)小明的父亲身高180厘米,体重80千克,试判断小明父亲的胖瘦情况
(2)某校为六年级学生进行了体检,下面是体检后得到的体重正常、体重偏轻和体重偏重的结果统计图.已知体重偏轻的有48人
①该校六年级学生有多少人?
②体重偏重的学生占体检总人数的百分之几?有多少人?
25.(8分)看图计算.(单位:cm,结果保留π)
(1)求阴影部分的面积,正方形边长为2cm.
(2)求阴影部分周长.(大圆直径8cm,小圆半径3cm)
26.(10分)列方程解应用题:如图,现有两条乡村公路AB、BC,AB长为1200米,BC长为1600米,一个人骑摩托车从A处以20m/s的速度匀速沿公路AB、BC向C处行驶;另一人骑自行车从B处以5m/s的速度从B向C行驶,并且两人同时出发.
(1)求经过多少秒摩托车追上自行车?
(2)求两人均在行驶途中时,经过多少秒两人在行进路线上相距150米?
27.(10分)列方程解应用题:已知A,B两地相距60千米,甲骑自行车,乙骑摩托车都沿一条笔直的公路由A地匀速行驶到B地,乙每小时比甲多行30千米,甲比乙早出发3小时,乙出发1小时后刚好追上甲.
(1)求甲的速度;
(2)问乙出发之后,到达B地之前,何时甲乙两人相距6千米;
(3)若丙骑自行车与甲同时出发,沿着这条笔直的公路由B地匀速行驶到A地,经过小时与乙相遇,求此时甲、丙两人之间距离.
参考答案与试题解析
一.选择题(共10小题,满分30分,每小题3分)
1.解:﹣2021的倒数为:﹣.
故选:A.
2.解:选项A、C、D能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以是轴对称图形,
选项B不能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以不是轴对称图形,
故选:B.
3.解:当|ab|>ab时,a、b一定异号;
当<0时,a、b一定异号;
当||=﹣,则≤0,a可能等于0,b≠0,a、b不一定异号;
当a3+b3=0,a3=﹣b3,即a3=(﹣b)3,
所以a=﹣b,有可能a=b=0,a、b不一定异号.
所以一定能够表示a、b异号的有①②.
故选:B.
4.解:18÷(﹣3)
=﹣(18÷3)
=﹣6.
故选:A.
5.解:∵AB=BC,
∴b﹣a=c﹣b,
∴a+c=2b,
∵a+b﹣c=0,即c=a+b,
∴a+(a+b)=2b,
∴b=2a,
∴c=a+b=3a,
∵a<b<c,
∴a>0,b>0,c>0,
∴a+c>0,则A选项错误;
ac>0,则B选项正确;
bc>0,则C错误;
ab>0,则D错误.
故选:B.
6.解:∵一个扇形的半径长为3,且圆心角为60°,
∴此扇形的弧长为=π.
故选:B.
7.解:取米作为共同的长度单位,那么AB=250米,A'B'=5厘米=0.05米,
所以==,
所以地图上的距离与实际距离的比为1:5000.
故选:B.
8.解:设他家该月用水x吨,
∵10×4=40<60,
∴10×4+(4+1)×(x﹣10)=60,
解得x=14,
答:他家该月用水14吨.
故选:B.
9.解:∵a※b=a2÷(b﹣1),
∴(﹣3)※4
=(﹣3)2÷(4﹣1)
=9÷3
=3,
故选:B.
10.解:∵P点关于OB的对称点是P1,P点关于OA的对称点是P2,
∴PM=P1M,PN=P2N,∠P2=∠P2PN,∠P1=∠P1PM,
∵∠AOB=40°,
∴∠P2PP1=140°,
∴∠P1+∠P2=40°,
∴∠PMN=∠P1+∠MPP1=2∠P1,∠PNM=∠P2+∠NPP2=2∠P2,
∴∠PMN+∠PNM=2×40°=80°,
∴∠MPN=180°﹣(∠PMN+∠PNM)=180°﹣80°=100°,
故选:B.
二.填空题(共10小题,满分30分,每小题3分)
11.解:在,﹣0.4,0. 2,3.14,0.1010010001…(每两个之间多一个0),120%,,100中,有理数有﹣0.4,0. 2,3.14,120%,,100等6个.
故答案为:6.
12.解:设第一个圆(大圆)的半径为r,
则第三个圆的半径为r=r,
∴第三个圆与第一个圆的面积之比为=,
故答案为:.
13.解:根据题意得,8﹣6.8=1.2(升),
1.2÷8=15%,
∴该汽车油耗下降率为15%.
故答案为:15%.
14.解:∵圆的周长是12.56米,
∴圆的半径为12.56÷2π=2米,
∴圆的面积为π×22=12.56(平方米),
故答案为:12.56平方米.
15.解:原式=﹣.
故答案为:.
16.解:由图可知,
第一行1个数字,
第二行2个数字,
第三行3个数字,
…,
则第n行n个数字,
前n行一共有个数字,
∵<2021<,2021﹣=2021﹣2016=5,
∴2021是表中第64行第5列,
故答案为:64,5.
17.解:设小长方形卡片的长为2m,则宽为m,
依题意,得:2m+2m=4,
解得:m=1,
∴2m=2.
再设盒子底部长方形的另一边长为x,
依题意,得:2(4+x﹣2):2×2(2+x﹣2)=5:6,
整理,得:10x=12+6x,
解得:x=3,
∴盒子底部长方形的面积=4×3=12.
故答案为:12.
18.解:(﹣9)÷×=(﹣9)××=﹣6×=﹣4,
故答案为:﹣4.
19.解:设C花卉一支x元,A花卉一支y元,则B花卉一支4x元,
∵每盒“如沐春风”礼盒的总成本是每盒“懵懂少女”礼盒总成本的2倍,
∴2y+4×4x+10x=2(2y+2×4x+4x),
化简整理得y=x,
∴A花卉一支x元,C花卉一支x元,B花卉一支4x元,
∴“如沐春风”礼盒每盒成本为2x+4×4x+10x=28x(元),以利润率50%定价为28x×(1+50%)=42x(元),打八折销售售价是42x×0.8=33.6x(元),
“懵懂少女”礼盒每盒成本为2x+2×4x+4x=14x(元),以利润率50%定价为14x×(1+50%)=21x(元),打八折销售售价是21x×0.8=16.8x(元),
“粉色回忆”礼盒每盒成本为2x+3×4x+6x=20x(元),以利润率50%定价为20x×(1+50%)=30x(元),打九折销售售价是30x×0.9=27x(元),
由某周末,该门市为了加大销量,将“如沐春风”、“懵懂少女”两种礼盒打八折进行销售,且两种礼盒的销量相同,设这两种礼盒都销售了a盒,粉色回忆”礼盒销售了b盒,根据三种礼盒的总成本恰好为总利润的4倍可得:
28x a+14x a+20x b=4[(33.6x﹣28x) a+(16.8x﹣14x) a+(27x﹣20x) b],
化简整理得:b=a,
∴该周末“粉色回忆”礼盒的总利润为(27x﹣20x) b=7x a=7.35xa,
该周末三种礼盒的总利润为(33.6x﹣28x) a+(16.8x﹣14x) a+(27x﹣20x) b=5.6xa+2.8xa+7.35xa=15.75xa,
∴该周末“粉色回忆”礼盒的总利润与三种礼盒的总利润的比值为=,
故答案为:.
20.解:设此圆锥的母线长为l,
根据题意得×2π×6×l=60π,解得l=10,
所以此圆锥的母线长为10.
故答案为10.
三.解答题(共7小题,满分60分)
21.解:(1)16÷(﹣2)3﹣(﹣)×(﹣4)+(﹣1)2020
=16÷(﹣8)﹣+1
=﹣2﹣+1
=﹣;
(2)﹣14﹣(1﹣0.5)××[2﹣(﹣3)2]
=﹣1﹣×(2﹣9)
=﹣1﹣×(﹣7)
=.
22.解:(1)x:4=6:2,
2x=24,
x=9;
(2)48÷﹣0.4x=4,
144﹣0.4x=4,
﹣0.4x=﹣140,
x=350;
(3)3x﹣1.2x=36,
1.8x=36,
x=20.
23.解:如图所示:
.
24.解:(1)×100%≈25%,
25%在24%~26%之间,属于偏胖的范围,
答:小明的父亲偏胖;
(2)①该校六年级学生有48÷8%=600(人);
②1﹣8%﹣54%=38%,
600×38%=228(人),
答:体重偏重的学生占体检总人数的38%,有228人.
25.解:(1)×2﹣2×2=(2π﹣4)cm2,
答:阴影部分的面积为(2π﹣4)cm2;
(2)×8π+×2π×3+4=(7π+4)cm,
答:阴影部分周长为(7π+4)cm.
26.解:(1)设经过x秒摩托车追上自行车,
20x=5x+1200,
解得x=80.
答:经过80秒摩托车追上自行车.
(2)(1200+1600)÷20=140(秒).
设经过y秒两人相距150米,
第一种情况:摩托车还差150米追上自行车时,
20y﹣1200=5y﹣150
解得y=70,符合题意.
第二种情况:摩托车超过自行车150米时,
20y=150+5y+1200
解得y=90,符合题意.
答:经过70秒或90秒两人在行进路线上相距150米.
27.解:(1)设甲速度为x千米/小时,则乙速度为(x+30)千米/小时
由题意可列方程:4x=x+30
解得:x=10
所以,甲速度为10千米/时;
(2)由(1)可知,甲速度为10千米/小时,乙速度为10+30=40千米/小时,
设乙出发后t小时甲乙相距6千米,则甲出发(t+3)小时,
相遇前:甲比乙多行驶6千米,可列方程10(t+3)﹣40t=6,
解得:t=0.8,
相遇后:乙比甲多行驶6千米,可列方程40t﹣10(t+3)=6,
解得t=1.2,
综上所述,乙出发0.8小时或1.2小时,甲乙相距6千米;
(3)设丙的速度为a千米/小时,丙与甲同时出发,所以丙行驶小时,乙行驶了﹣3=(小时).
根据题意可列方程a+×40=60,
解得:a=10,
所以丙的速度为10千米/小时,
经过小时,丙行驶×10=36(千米),甲行驶×10=36(千米),
所以两人相距36+36﹣60=12(千米).
同课章节目录
