2021-2022学年人教版(五四制)七年级上学期数学期末练习试卷(word版含答案)
文档属性
| 名称 | 2021-2022学年人教版(五四制)七年级上学期数学期末练习试卷(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 371.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-26 11:29:26 | ||
图片预览



文档简介
2021-2022学年人教五四新版七年级上学期数学期末练习试卷一.选择题(共10小题,满分30分,每小题3分)
1.若点P(x,y)在第四象限,且|x|=2,|y|=3,则x+y=( )
A.﹣1 B.1 C.5 D.﹣5
2.下列方程中:①2x+4=6,②x﹣1=,③3x2﹣2x,④5x<7,⑤3x﹣2y=2,⑥x=3,其中是一元一次方程的有( )
A.5个 B.4个 C.3个 D.2个
3.﹣可以表示( )
A.0.2的平方根 B.﹣0.2的算术平方根
C.0.2的负的平方根 D.﹣0.2的平方根
4.下列四个图案中,运用了图形的平移进行图案设计的是( )
A. B.
C. D.
5.在0.,,﹣1,四个数中,属于无理数的是( )
A.0. B. C.﹣1 D.
6.如图,直线AB、CD相交于点O,OE平分∠AOC,若∠AOE=35°,则∠BOC的度数是( )
A.110° B.50° C.60° D.70°
7.下列说法错误的是( )
A.若a=b,则ac=bc
B.若b=1,则ab=a
C.若,则a=b
D.若(a﹣1)c=(b﹣1)c,则a=b
8.如图,直线AB∥CD∥EF,点O在直线EF上,下列结论正确的是( )
A.∠α+∠β﹣∠γ=90° B.∠α+∠γ﹣∠β=180°
C.∠γ+∠β﹣∠α=180° D.∠α+∠β+∠γ=180°
9.一项工程,甲单独做5天完成,乙单独做8天完成.若甲先做1天,然后甲、乙合作完成此项工作的.若设甲一共做了x天,则所列方程为( )
A. B. C. D.
10.有下列命题,其中假命题有( )
①的算术平方根是2.
②一个角的邻补角一定大于这个角.
③在同一平面内,垂直于同一条直线的两直线平行.
④平行于同一条直线的两条直线互相平行.
A.①② B.①③ C.②④ D.③④
二.填空题(共10小题,满分30分,每小题3分)
11.已知|x|=,则x= .
12.x的3倍与4的和等于x的5倍与2的差,方程可列为 .
13.点C在∠AOB的边OA上,过点C作CD⊥OB,过点C作OA的垂线交射线OB于点E,若∠AOB=66°,则∠DCE是 度.
14.若x=﹣1是方程2x﹣3a=7的解,则关于x的方程a(3x﹣1)=4x+a﹣2的解为 .
15.如果点P(x,y)的坐标满足x+y=xy,那么称点P为“和谐点”,若某个“和谐点“P到x轴的距离为2,则P点的坐标为 .
16.比较大小: (填“>”,“<”或“=”).
17.今年国庆长假期间,“富万家”超市某商品按标价打八折销售,小玲购了一件该商品,付款56元,则该项商品的标价为 元.
18.把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G,D、C分别在M、N的位置上,若∠EFG=50°,则∠2﹣∠1= .
19.,观察下列等式:4﹣1=3,9﹣4=5,16﹣9=7,25﹣16=9,….按照上述规律,第n个的等式为: .
20.如图,已知△ABC中,,点D是AB边的中点,连接CD,将△BCD沿CD翻折,点B的对应点是点B′,CB′交AB于点E,连接AB′,若,则点B′到直线AC的距离为 .
三.解答题(共7小题,满分60分)
21.(6分)计算:3÷×﹣.
22.(8分)解方程:
①2x+5=3(x﹣1);
②﹣=1.
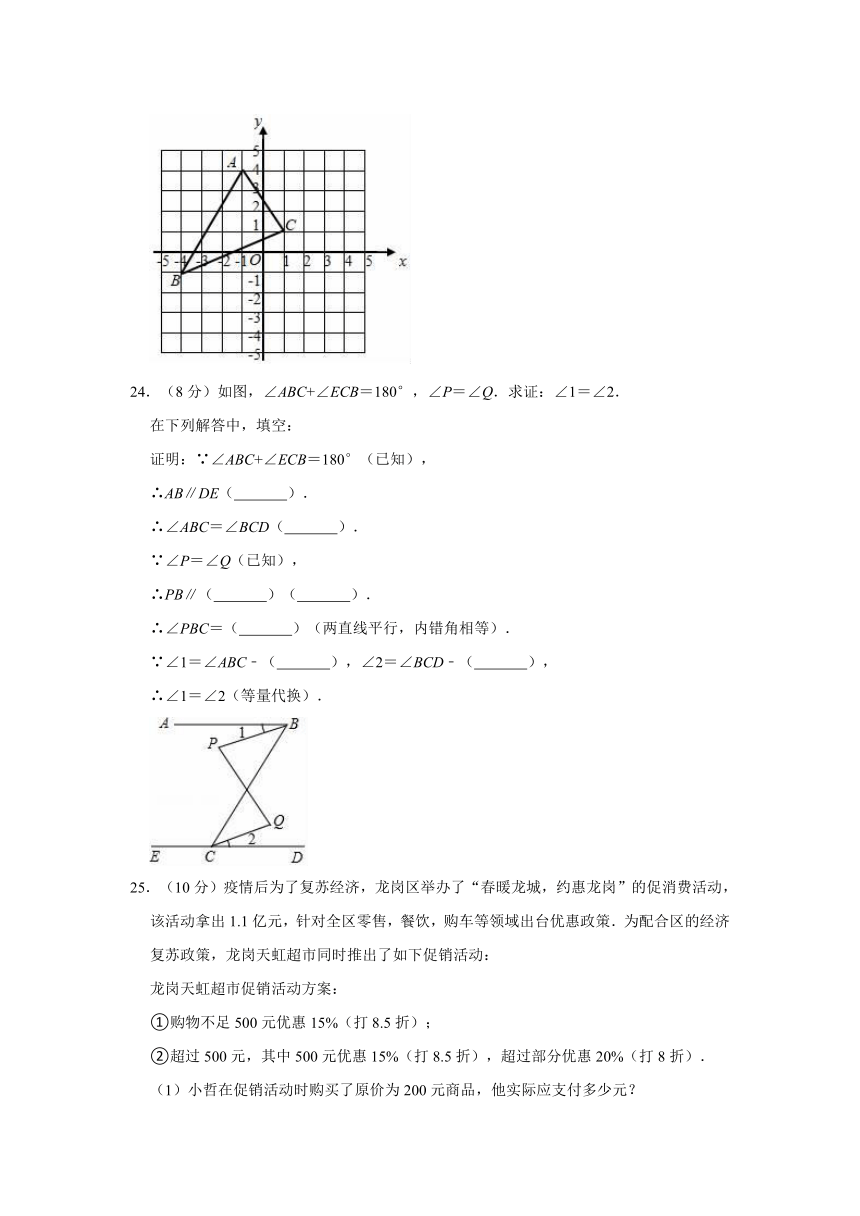
23.(8分)三角形ABC在平面直角坐标系中的位置如图所示,点O为坐标原点,A(﹣1,4),B(﹣4,﹣1),C(1,1).将三角形ABC向右平移3个单位长度,再向下平移2个单位长度得到三角形A1B1C1.
(1)画出平移后的三角形;
(2)直接写出点A1,B1,C1的坐标:A1( , ),B1( , ),C1( , );
(3)请直接写出三角形的面积为 .
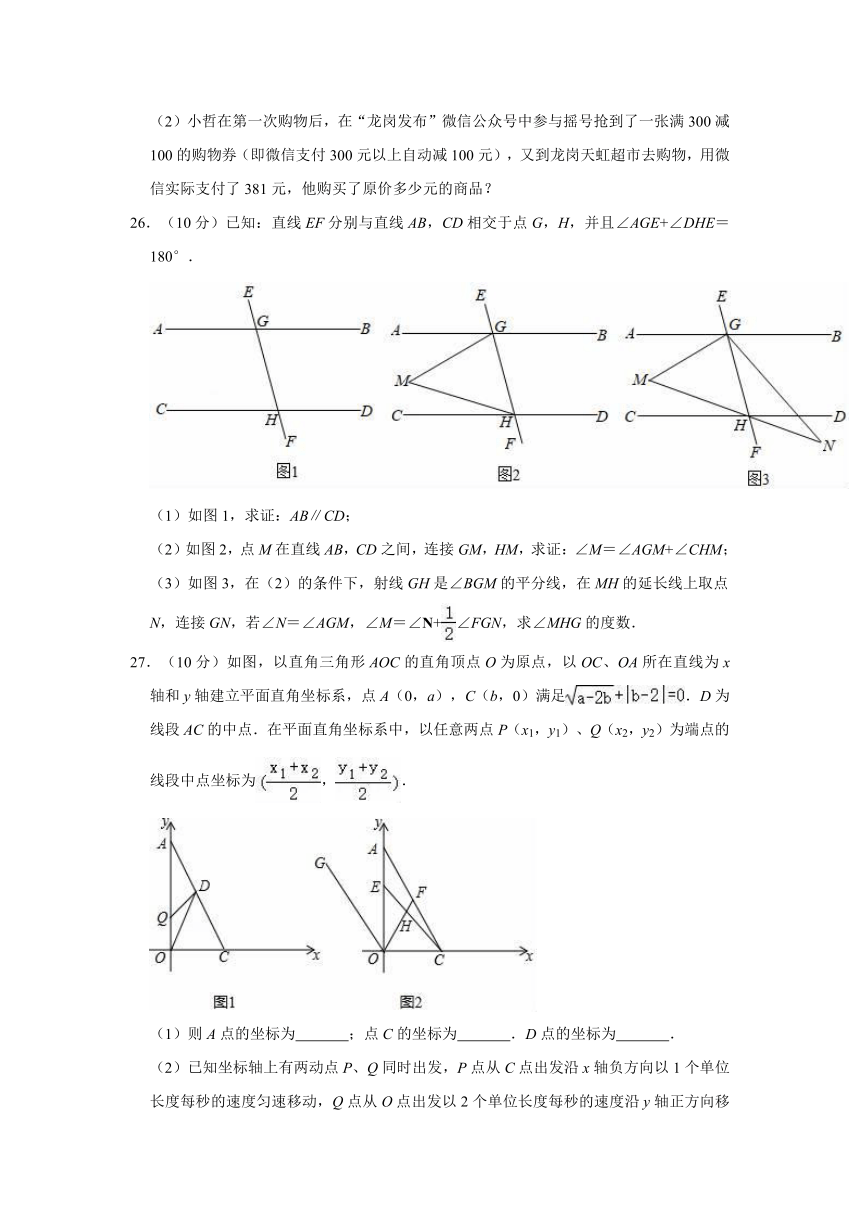
24.(8分)如图,∠ABC+∠ECB=180°,∠P=∠Q.求证:∠1=∠2.
在下列解答中,填空:
证明:∵∠ABC+∠ECB=180°(已知),
∴AB∥DE( ).
∴∠ABC=∠BCD( ).
∵∠P=∠Q(已知),
∴PB∥( )( ).
∴∠PBC=( )(两直线平行,内错角相等).
∵∠1=∠ABC﹣( ),∠2=∠BCD﹣( ),
∴∠1=∠2(等量代换).
25.(10分)疫情后为了复苏经济,龙岗区举办了“春暖龙城,约惠龙岗”的促消费活动,该活动拿出1.1亿元,针对全区零售,餐饮,购车等领域出台优惠政策.为配合区的经济复苏政策,龙岗天虹超市同时推出了如下促销活动:
龙岗天虹超市促销活动方案:
①购物不足500元优惠15%(打8.5折);
②超过500元,其中500元优惠15%(打8.5折),超过部分优惠20%(打8折).
(1)小哲在促销活动时购买了原价为200元商品,他实际应支付多少元?
(2)小哲在第一次购物后,在“龙岗发布”微信公众号中参与摇号抢到了一张满300减100的购物券(即微信支付300元以上自动减100元),又到龙岗天虹超市去购物,用微信实际支付了381元,他购买了原价多少元的商品?
26.(10分)已知:直线EF分别与直线AB,CD相交于点G,H,并且∠AGE+∠DHE=180°.
(1)如图1,求证:AB∥CD;
(2)如图2,点M在直线AB,CD之间,连接GM,HM,求证:∠M=∠AGM+∠CHM;
(3)如图3,在(2)的条件下,射线GH是∠BGM的平分线,在MH的延长线上取点N,连接GN,若∠N=∠AGM,∠M=∠N+∠FGN,求∠MHG的度数.
27.(10分)如图,以直角三角形AOC的直角顶点O为原点,以OC、OA所在直线为x轴和y轴建立平面直角坐标系,点A(0,a),C(b,0)满足.D为线段AC的中点.在平面直角坐标系中,以任意两点P(x1,y1)、Q(x2,y2)为端点的线段中点坐标为,.
(1)则A点的坐标为 ;点C的坐标为 .D点的坐标为 .
(2)已知坐标轴上有两动点P、Q同时出发,P点从C点出发沿x轴负方向以1个单位长度每秒的速度匀速移动,Q点从O点出发以2个单位长度每秒的速度沿y轴正方向移动,点Q到达A点整个运动随之结束.设运动时间为t(t>0)秒.问:是否存在这样的t,使S△ODP=S△ODQ,若存在,请求出t的值;若不存在,请说明理由.
(3)点F是线段AC上一点,满足∠FOC=∠FCO,点G是第二象限中一点,连OG,使得∠AOG=∠AOF.点E是线段OA上一动点,连CE交OF于点H,当点E在线段OA上运动的过程中,的值是否会发生变化?若不变,请求出它的值;若变化,请说明理由.
参考答案与试题解析
一.选择题(共10小题,满分30分,每小题3分)
1.解:由题意,得
x=2,y=﹣3,
x+y=2+(﹣3)=﹣1,
故选:A.
2.解:①2x+4=6是一元一次方程;
②x﹣1=是分式方程;
③3x2﹣2x不是方程,是代数式;
④5x<7是一元一次不等式;
⑤3x﹣2y=2是二元一次方程;
⑥x=3是一元一次方程;
一元一次方程共2个,
故选:D.
3.解:﹣可以表示0.2的负的平方根,
故选:C.
4.解:A、图案属于轴对称变换和平移所得到,故此选项不合题意;
B、图案属于相似所得到,故此选项不合题意;
C、图案属于轴对称变换和平移所得到,故此选项不合题意;
D、图案形状与大小没有改变,符合平移性质,故此选项符合题意.
故选:D.
5.解:A、0.是循环小数,属于有理数,故本选项不合题意;
B、,是整数,属于有理数,故本选项不合题意;
C、﹣1是整数,属于有理数,故本选项不合题意;
D、是无理数,故本选项符合题意.
故选:D.
6.解:∵OE平分∠AOC,∠AOE=35°,
∴∠AOC=2∠AOE=70°,
∴∠BOC=180°﹣∠AOC=110°,
故选:A.
7.解:(D)当c=0时,则a不一定等于b,故D错误;
故选:D.
8.解:∵AB∥EF,
∴∠α=∠BOF,
∵CD∥EF,
∴∠γ+∠COF=180°,
∵∠BOF=∠COF+∠β,
∴∠γ+∠α﹣∠β=180°,
故选:B.
9.解:设甲一共做了x天,
由题意得: +=,
故选:B.
10.解:①=2的算术平方根是,故错误,是假命题,符合题意.
②一个角的邻补角不一定大于这个角,错误,是假命题,符合题意.
③在同一平面内,垂直于同一条直线的两直线平行,正确,是真命题,不符合题意.
④平行于同一条直线的两条直线互相平行,正确,是真命题,不符合题意.
故选:A.
二.填空题(共10小题,满分30分,每小题3分)
11.解:|x|=,
.
故答案为:.
12.解:根据题意得:
3x+4=5x﹣2,
故答案为:3x+4=5x﹣2.
13.解:如图1,∵CD⊥OB,∠AOB=66°,
∴∠OCD=90°﹣∠AOB=90°﹣66°=24°,
∵CE⊥OA,∴∠OCE=90°,
∴∠DCE=90°﹣∠OCD=90°﹣24°=66°,
如图2,∵CD⊥OB,∠AOB=66°,
∴∠OCF=90°﹣∠AOB=90°﹣66°
=24°=∠ACD,
∵CE⊥OA,∴∠OCE=90°,
∴∠DCE=90°+∠OCD=90°+24°=114°,
故答案为:66或114.
14.解:∵x=﹣1是方程2x﹣3a=7的解,
∴﹣2﹣3a=7,
∴a=﹣3,
把﹣3代入方程a(3x﹣1)=4x+a﹣2得:﹣3(3x﹣1)=4x﹣5,
解得:x=,
故答案为x=.
15.解:设P点的坐标为(x,y),
∵“和谐点“P到x轴的距离为2,
∴|y|=2,
∴y=±2.
将y=2代入x+y=xy,得x+2=2x,解得x=2,
∴P点的坐标为(2,2);
将y=﹣2代入x+y=xy,得x﹣2=﹣2x,解得x=,
∴P点的坐标为(,﹣2).
综上所述,所求P点的坐标为(2,2)或(,﹣2).
故答案为(2,2)或(,﹣2).
16.解:∵()2=3.5==,()2=,
而>,
∴>.
故答案为>.
17.设购买这件商品花了x元,
由题意得:0.8x=56
解得:x=70
故答案为70元.
18.解:由题意可得:∠DEF=∠GEF.
∵DE∥BC,
∴∠DEF=∠EFG=50°.
∴∠DEF=∠GEF=∠EFG=50°.
∴∠1=180°﹣∠GFD=180°﹣100=80°.
∵AE∥BG,
∴∠1+∠2=180°.
∴∠2=100°.
∴∠2﹣∠1=100°﹣80°=20°.
故答案为:20°.
19.解:因为第一项为4﹣1=3可以表示为22﹣12=2×1+1,
第二项为9﹣4=5可以表示为32﹣22=2×2+1,
第三项为16﹣9=7可以表示为42﹣32=2×3+1,
第四项为25﹣16=9可以表示为52﹣42=2×4+1,
故第n个等式可以表示为(n+1)2﹣n2=2n+1.
20.解:作BF⊥AF交CA的延长线于点F,如图,
,
∵D是AB边中点,
∴S△BDC=S△ACD=2+=,
∵△BDC与△B′DC关于CD对称,
∴S△BDC=S△B'DC=,
∴S△B′DE=,
∴
解得S△AB′E=,
∴S△AB′C==,
∵S△AB′C=
=,
解得B'F=,
故答案为.
三.解答题(共7小题,满分60分)
21.解:原式=3÷2×﹣
=﹣
=﹣.
22.解:①2x+5=3(x﹣1),
去括号,得2x+5=3x﹣3,
移项,得2x﹣3x=﹣3﹣5,
合并同类项,得﹣x=﹣8,
系数化为1,得x=8;
②﹣=1,
去分母,得2(2x+1)﹣(5x﹣1)=6,
去括号,得4x+2﹣5x+1=6,
移项,得4x﹣5x=6﹣2﹣1,
合并同类项,得﹣x=3,
系数化1,得x=﹣3.
23.解:(1)如图所示,
△A1B1C1即为所求.
(2)A1(2,2),B1(﹣1,﹣3),C1(4,﹣1),
(3)△ABC的面积==,
故答案为:(2)2;2;﹣1;﹣3;4;﹣1;(3).
24.证明:∵∠ABC+∠ECB=180°(已知),
∴AB∥DE(同旁内角互补,两直线平行).
∴∠ABC=∠BCD(两直线平行,内错角相等).
∵∠P=∠Q(已知),
∴PB∥(CQ)(内错角相等,两直线平行).
∴∠PBC=(∠BCQ)(两直线平行,内错角相等).
∵∠1=∠ABC﹣(∠PBC),∠2=∠BCD﹣(∠BCQ),
∴∠1=∠2(等量代换).
故答案为:同旁内角互补,两直线平行;两直线平行,内错角相等;CQ,内错角相等,两直线平行;∠BCQ;∠PBC;∠BCQ.
25.解:(1)200×(1﹣15%)=170(元).
故他实际应支付170元;
(2)设他购买了原价x元的商品,依题意有
500×(1﹣15%)+(1﹣20%)(x﹣500)﹣100=381,
解得x=570.
故他购买了原价570元的商品.
26.(1)证明:如图1,∵∠AGE+∠DHE=180°,∠AGE=∠BGF.
∴∠BGF+∠DHE=180°,
∴AB∥CD;
(2)证明:如图2,过点M作MR∥AB,
又∵AB∥CD,
∴AB∥CD∥MR.
∴∠GMR=∠AGM,∠HMR=∠CHM.
∴∠GMH=∠GMR+∠RMH=∠AGM+∠CHM.
(3)解:如图3,令∠AGM=2α,∠CHM=β,则∠N=2α,∠M=2α+β,
∵射线GH是∠BGM的平分线,
∴,
∴∠AGH=∠AGM+∠FGM=2α+90°﹣α=90°+α,
∵,
∴,
∴∠FGN=2β,
过点H作HT∥GN,
则∠MHT=∠N=2α,∠GHT=∠FGN=2β,
∴∠GHM=∠MHT+∠GHT=2α+2β,
∠CHG=∠CHM+∠MHT+∠GHT=β+2α+2β=2α+3β,
∵AB∥CD,
∴∠AGH+∠CHG=180°,
∴90°+α+2α+3β=180°,
∴α+β=30°,
∴∠GHM=2(α+β)=60°.
27.解:(1)∵.
∴a﹣2b=0,b﹣2=0,
解得a=4,b=2,
∴A(0,4),C(2,0);
∴x==1,y==2,
∴D(1,2).
故答案为(0,4),(2,0),(1,2).
(2)如图1中,
由条件可知:P点从C点运动到O点时间为2秒,Q点从O点运动到A点时间为2秒,
∴0<t≤2时,点Q在线段AO上,
即 CP=t,OP=2﹣t,OQ=2t,AQ=4﹣2t,
∴S△DOP=OP yD=(2﹣t)×2=2﹣t,S△DOQ=OQ xD=×2t×1=t,
∵S△ODP=S△ODQ,
∴2﹣t=t,
∴t=1;
(3)的值不变,其值为2.理由如下:如图2中,
∵∠2+∠3=90°,
又∵∠1=∠2,∠3=∠FCO,
∴∠GOC+∠ACO=180°,
∴OG∥AC,
∴∠1=∠CAO,
∴∠OEC=∠CAO+∠4=∠1+∠4,
如图,过H点作AC的平行线,交x轴于P,则∠4=∠PHC,PH∥OG,
∴∠PHO=∠GOF=∠1+∠2,
∴∠OHC=∠OHP+∠PHC=∠GOF+∠4=∠1+∠2+∠4,
∴=,
=,
=2.
1.若点P(x,y)在第四象限,且|x|=2,|y|=3,则x+y=( )
A.﹣1 B.1 C.5 D.﹣5
2.下列方程中:①2x+4=6,②x﹣1=,③3x2﹣2x,④5x<7,⑤3x﹣2y=2,⑥x=3,其中是一元一次方程的有( )
A.5个 B.4个 C.3个 D.2个
3.﹣可以表示( )
A.0.2的平方根 B.﹣0.2的算术平方根
C.0.2的负的平方根 D.﹣0.2的平方根
4.下列四个图案中,运用了图形的平移进行图案设计的是( )
A. B.
C. D.
5.在0.,,﹣1,四个数中,属于无理数的是( )
A.0. B. C.﹣1 D.
6.如图,直线AB、CD相交于点O,OE平分∠AOC,若∠AOE=35°,则∠BOC的度数是( )
A.110° B.50° C.60° D.70°
7.下列说法错误的是( )
A.若a=b,则ac=bc
B.若b=1,则ab=a
C.若,则a=b
D.若(a﹣1)c=(b﹣1)c,则a=b
8.如图,直线AB∥CD∥EF,点O在直线EF上,下列结论正确的是( )
A.∠α+∠β﹣∠γ=90° B.∠α+∠γ﹣∠β=180°
C.∠γ+∠β﹣∠α=180° D.∠α+∠β+∠γ=180°
9.一项工程,甲单独做5天完成,乙单独做8天完成.若甲先做1天,然后甲、乙合作完成此项工作的.若设甲一共做了x天,则所列方程为( )
A. B. C. D.
10.有下列命题,其中假命题有( )
①的算术平方根是2.
②一个角的邻补角一定大于这个角.
③在同一平面内,垂直于同一条直线的两直线平行.
④平行于同一条直线的两条直线互相平行.
A.①② B.①③ C.②④ D.③④
二.填空题(共10小题,满分30分,每小题3分)
11.已知|x|=,则x= .
12.x的3倍与4的和等于x的5倍与2的差,方程可列为 .
13.点C在∠AOB的边OA上,过点C作CD⊥OB,过点C作OA的垂线交射线OB于点E,若∠AOB=66°,则∠DCE是 度.
14.若x=﹣1是方程2x﹣3a=7的解,则关于x的方程a(3x﹣1)=4x+a﹣2的解为 .
15.如果点P(x,y)的坐标满足x+y=xy,那么称点P为“和谐点”,若某个“和谐点“P到x轴的距离为2,则P点的坐标为 .
16.比较大小: (填“>”,“<”或“=”).
17.今年国庆长假期间,“富万家”超市某商品按标价打八折销售,小玲购了一件该商品,付款56元,则该项商品的标价为 元.
18.把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G,D、C分别在M、N的位置上,若∠EFG=50°,则∠2﹣∠1= .
19.,观察下列等式:4﹣1=3,9﹣4=5,16﹣9=7,25﹣16=9,….按照上述规律,第n个的等式为: .
20.如图,已知△ABC中,,点D是AB边的中点,连接CD,将△BCD沿CD翻折,点B的对应点是点B′,CB′交AB于点E,连接AB′,若,则点B′到直线AC的距离为 .
三.解答题(共7小题,满分60分)
21.(6分)计算:3÷×﹣.
22.(8分)解方程:
①2x+5=3(x﹣1);
②﹣=1.
23.(8分)三角形ABC在平面直角坐标系中的位置如图所示,点O为坐标原点,A(﹣1,4),B(﹣4,﹣1),C(1,1).将三角形ABC向右平移3个单位长度,再向下平移2个单位长度得到三角形A1B1C1.
(1)画出平移后的三角形;
(2)直接写出点A1,B1,C1的坐标:A1( , ),B1( , ),C1( , );
(3)请直接写出三角形的面积为 .
24.(8分)如图,∠ABC+∠ECB=180°,∠P=∠Q.求证:∠1=∠2.
在下列解答中,填空:
证明:∵∠ABC+∠ECB=180°(已知),
∴AB∥DE( ).
∴∠ABC=∠BCD( ).
∵∠P=∠Q(已知),
∴PB∥( )( ).
∴∠PBC=( )(两直线平行,内错角相等).
∵∠1=∠ABC﹣( ),∠2=∠BCD﹣( ),
∴∠1=∠2(等量代换).
25.(10分)疫情后为了复苏经济,龙岗区举办了“春暖龙城,约惠龙岗”的促消费活动,该活动拿出1.1亿元,针对全区零售,餐饮,购车等领域出台优惠政策.为配合区的经济复苏政策,龙岗天虹超市同时推出了如下促销活动:
龙岗天虹超市促销活动方案:
①购物不足500元优惠15%(打8.5折);
②超过500元,其中500元优惠15%(打8.5折),超过部分优惠20%(打8折).
(1)小哲在促销活动时购买了原价为200元商品,他实际应支付多少元?
(2)小哲在第一次购物后,在“龙岗发布”微信公众号中参与摇号抢到了一张满300减100的购物券(即微信支付300元以上自动减100元),又到龙岗天虹超市去购物,用微信实际支付了381元,他购买了原价多少元的商品?
26.(10分)已知:直线EF分别与直线AB,CD相交于点G,H,并且∠AGE+∠DHE=180°.
(1)如图1,求证:AB∥CD;
(2)如图2,点M在直线AB,CD之间,连接GM,HM,求证:∠M=∠AGM+∠CHM;
(3)如图3,在(2)的条件下,射线GH是∠BGM的平分线,在MH的延长线上取点N,连接GN,若∠N=∠AGM,∠M=∠N+∠FGN,求∠MHG的度数.
27.(10分)如图,以直角三角形AOC的直角顶点O为原点,以OC、OA所在直线为x轴和y轴建立平面直角坐标系,点A(0,a),C(b,0)满足.D为线段AC的中点.在平面直角坐标系中,以任意两点P(x1,y1)、Q(x2,y2)为端点的线段中点坐标为,.
(1)则A点的坐标为 ;点C的坐标为 .D点的坐标为 .
(2)已知坐标轴上有两动点P、Q同时出发,P点从C点出发沿x轴负方向以1个单位长度每秒的速度匀速移动,Q点从O点出发以2个单位长度每秒的速度沿y轴正方向移动,点Q到达A点整个运动随之结束.设运动时间为t(t>0)秒.问:是否存在这样的t,使S△ODP=S△ODQ,若存在,请求出t的值;若不存在,请说明理由.
(3)点F是线段AC上一点,满足∠FOC=∠FCO,点G是第二象限中一点,连OG,使得∠AOG=∠AOF.点E是线段OA上一动点,连CE交OF于点H,当点E在线段OA上运动的过程中,的值是否会发生变化?若不变,请求出它的值;若变化,请说明理由.
参考答案与试题解析
一.选择题(共10小题,满分30分,每小题3分)
1.解:由题意,得
x=2,y=﹣3,
x+y=2+(﹣3)=﹣1,
故选:A.
2.解:①2x+4=6是一元一次方程;
②x﹣1=是分式方程;
③3x2﹣2x不是方程,是代数式;
④5x<7是一元一次不等式;
⑤3x﹣2y=2是二元一次方程;
⑥x=3是一元一次方程;
一元一次方程共2个,
故选:D.
3.解:﹣可以表示0.2的负的平方根,
故选:C.
4.解:A、图案属于轴对称变换和平移所得到,故此选项不合题意;
B、图案属于相似所得到,故此选项不合题意;
C、图案属于轴对称变换和平移所得到,故此选项不合题意;
D、图案形状与大小没有改变,符合平移性质,故此选项符合题意.
故选:D.
5.解:A、0.是循环小数,属于有理数,故本选项不合题意;
B、,是整数,属于有理数,故本选项不合题意;
C、﹣1是整数,属于有理数,故本选项不合题意;
D、是无理数,故本选项符合题意.
故选:D.
6.解:∵OE平分∠AOC,∠AOE=35°,
∴∠AOC=2∠AOE=70°,
∴∠BOC=180°﹣∠AOC=110°,
故选:A.
7.解:(D)当c=0时,则a不一定等于b,故D错误;
故选:D.
8.解:∵AB∥EF,
∴∠α=∠BOF,
∵CD∥EF,
∴∠γ+∠COF=180°,
∵∠BOF=∠COF+∠β,
∴∠γ+∠α﹣∠β=180°,
故选:B.
9.解:设甲一共做了x天,
由题意得: +=,
故选:B.
10.解:①=2的算术平方根是,故错误,是假命题,符合题意.
②一个角的邻补角不一定大于这个角,错误,是假命题,符合题意.
③在同一平面内,垂直于同一条直线的两直线平行,正确,是真命题,不符合题意.
④平行于同一条直线的两条直线互相平行,正确,是真命题,不符合题意.
故选:A.
二.填空题(共10小题,满分30分,每小题3分)
11.解:|x|=,
.
故答案为:.
12.解:根据题意得:
3x+4=5x﹣2,
故答案为:3x+4=5x﹣2.
13.解:如图1,∵CD⊥OB,∠AOB=66°,
∴∠OCD=90°﹣∠AOB=90°﹣66°=24°,
∵CE⊥OA,∴∠OCE=90°,
∴∠DCE=90°﹣∠OCD=90°﹣24°=66°,
如图2,∵CD⊥OB,∠AOB=66°,
∴∠OCF=90°﹣∠AOB=90°﹣66°
=24°=∠ACD,
∵CE⊥OA,∴∠OCE=90°,
∴∠DCE=90°+∠OCD=90°+24°=114°,
故答案为:66或114.
14.解:∵x=﹣1是方程2x﹣3a=7的解,
∴﹣2﹣3a=7,
∴a=﹣3,
把﹣3代入方程a(3x﹣1)=4x+a﹣2得:﹣3(3x﹣1)=4x﹣5,
解得:x=,
故答案为x=.
15.解:设P点的坐标为(x,y),
∵“和谐点“P到x轴的距离为2,
∴|y|=2,
∴y=±2.
将y=2代入x+y=xy,得x+2=2x,解得x=2,
∴P点的坐标为(2,2);
将y=﹣2代入x+y=xy,得x﹣2=﹣2x,解得x=,
∴P点的坐标为(,﹣2).
综上所述,所求P点的坐标为(2,2)或(,﹣2).
故答案为(2,2)或(,﹣2).
16.解:∵()2=3.5==,()2=,
而>,
∴>.
故答案为>.
17.设购买这件商品花了x元,
由题意得:0.8x=56
解得:x=70
故答案为70元.
18.解:由题意可得:∠DEF=∠GEF.
∵DE∥BC,
∴∠DEF=∠EFG=50°.
∴∠DEF=∠GEF=∠EFG=50°.
∴∠1=180°﹣∠GFD=180°﹣100=80°.
∵AE∥BG,
∴∠1+∠2=180°.
∴∠2=100°.
∴∠2﹣∠1=100°﹣80°=20°.
故答案为:20°.
19.解:因为第一项为4﹣1=3可以表示为22﹣12=2×1+1,
第二项为9﹣4=5可以表示为32﹣22=2×2+1,
第三项为16﹣9=7可以表示为42﹣32=2×3+1,
第四项为25﹣16=9可以表示为52﹣42=2×4+1,
故第n个等式可以表示为(n+1)2﹣n2=2n+1.
20.解:作BF⊥AF交CA的延长线于点F,如图,
,
∵D是AB边中点,
∴S△BDC=S△ACD=2+=,
∵△BDC与△B′DC关于CD对称,
∴S△BDC=S△B'DC=,
∴S△B′DE=,
∴
解得S△AB′E=,
∴S△AB′C==,
∵S△AB′C=
=,
解得B'F=,
故答案为.
三.解答题(共7小题,满分60分)
21.解:原式=3÷2×﹣
=﹣
=﹣.
22.解:①2x+5=3(x﹣1),
去括号,得2x+5=3x﹣3,
移项,得2x﹣3x=﹣3﹣5,
合并同类项,得﹣x=﹣8,
系数化为1,得x=8;
②﹣=1,
去分母,得2(2x+1)﹣(5x﹣1)=6,
去括号,得4x+2﹣5x+1=6,
移项,得4x﹣5x=6﹣2﹣1,
合并同类项,得﹣x=3,
系数化1,得x=﹣3.
23.解:(1)如图所示,
△A1B1C1即为所求.
(2)A1(2,2),B1(﹣1,﹣3),C1(4,﹣1),
(3)△ABC的面积==,
故答案为:(2)2;2;﹣1;﹣3;4;﹣1;(3).
24.证明:∵∠ABC+∠ECB=180°(已知),
∴AB∥DE(同旁内角互补,两直线平行).
∴∠ABC=∠BCD(两直线平行,内错角相等).
∵∠P=∠Q(已知),
∴PB∥(CQ)(内错角相等,两直线平行).
∴∠PBC=(∠BCQ)(两直线平行,内错角相等).
∵∠1=∠ABC﹣(∠PBC),∠2=∠BCD﹣(∠BCQ),
∴∠1=∠2(等量代换).
故答案为:同旁内角互补,两直线平行;两直线平行,内错角相等;CQ,内错角相等,两直线平行;∠BCQ;∠PBC;∠BCQ.
25.解:(1)200×(1﹣15%)=170(元).
故他实际应支付170元;
(2)设他购买了原价x元的商品,依题意有
500×(1﹣15%)+(1﹣20%)(x﹣500)﹣100=381,
解得x=570.
故他购买了原价570元的商品.
26.(1)证明:如图1,∵∠AGE+∠DHE=180°,∠AGE=∠BGF.
∴∠BGF+∠DHE=180°,
∴AB∥CD;
(2)证明:如图2,过点M作MR∥AB,
又∵AB∥CD,
∴AB∥CD∥MR.
∴∠GMR=∠AGM,∠HMR=∠CHM.
∴∠GMH=∠GMR+∠RMH=∠AGM+∠CHM.
(3)解:如图3,令∠AGM=2α,∠CHM=β,则∠N=2α,∠M=2α+β,
∵射线GH是∠BGM的平分线,
∴,
∴∠AGH=∠AGM+∠FGM=2α+90°﹣α=90°+α,
∵,
∴,
∴∠FGN=2β,
过点H作HT∥GN,
则∠MHT=∠N=2α,∠GHT=∠FGN=2β,
∴∠GHM=∠MHT+∠GHT=2α+2β,
∠CHG=∠CHM+∠MHT+∠GHT=β+2α+2β=2α+3β,
∵AB∥CD,
∴∠AGH+∠CHG=180°,
∴90°+α+2α+3β=180°,
∴α+β=30°,
∴∠GHM=2(α+β)=60°.
27.解:(1)∵.
∴a﹣2b=0,b﹣2=0,
解得a=4,b=2,
∴A(0,4),C(2,0);
∴x==1,y==2,
∴D(1,2).
故答案为(0,4),(2,0),(1,2).
(2)如图1中,
由条件可知:P点从C点运动到O点时间为2秒,Q点从O点运动到A点时间为2秒,
∴0<t≤2时,点Q在线段AO上,
即 CP=t,OP=2﹣t,OQ=2t,AQ=4﹣2t,
∴S△DOP=OP yD=(2﹣t)×2=2﹣t,S△DOQ=OQ xD=×2t×1=t,
∵S△ODP=S△ODQ,
∴2﹣t=t,
∴t=1;
(3)的值不变,其值为2.理由如下:如图2中,
∵∠2+∠3=90°,
又∵∠1=∠2,∠3=∠FCO,
∴∠GOC+∠ACO=180°,
∴OG∥AC,
∴∠1=∠CAO,
∴∠OEC=∠CAO+∠4=∠1+∠4,
如图,过H点作AC的平行线,交x轴于P,则∠4=∠PHC,PH∥OG,
∴∠PHO=∠GOF=∠1+∠2,
∴∠OHC=∠OHP+∠PHC=∠GOF+∠4=∠1+∠2+∠4,
∴=,
=,
=2.
同课章节目录
