第二十章解直角三角形课后培优2021-2022学年京改版九年级数学上册(word版含解析)
文档属性
| 名称 | 第二十章解直角三角形课后培优2021-2022学年京改版九年级数学上册(word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 433.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-26 09:48:31 | ||
图片预览




文档简介
第二十章 解直角三角形
一、单选题
1.如图,在ABC中,∠A=120°,AB=4,AC=2,则sinB的值是( )
A. B. C. D.
2.如图,△ABC的顶点都在方格纸的格点上,那么的值为( )
A. B. C. D.
3.要使式子有意义,则α可以取下列数值中的(D)
A.17° B.19°
C.21° D.24°
4.如图所示,在高为2 m,坡角为30°的楼梯上铺地毯,则地毯的长度至少应为( ).
A.4 m B.6 m C.m D.
5.某校数学兴趣小组要测量摩天轮的高度.如图,他们在C处测得摩天轮的最高点A的仰角为45°,再往摩天轮的方向前进50 m至D处,测得最高点A的仰角为60°.问摩天轮的高度AB约是( )
(结果精确到1 米,参考数据:≈1.41,≈1.73)
A.120米 B.117米 C.118米 D.119米
6.如图,在△ABC中,cosB=,sinC=,AC=5,则△ABC的面积是( )
A. B.12 C.14 D.21
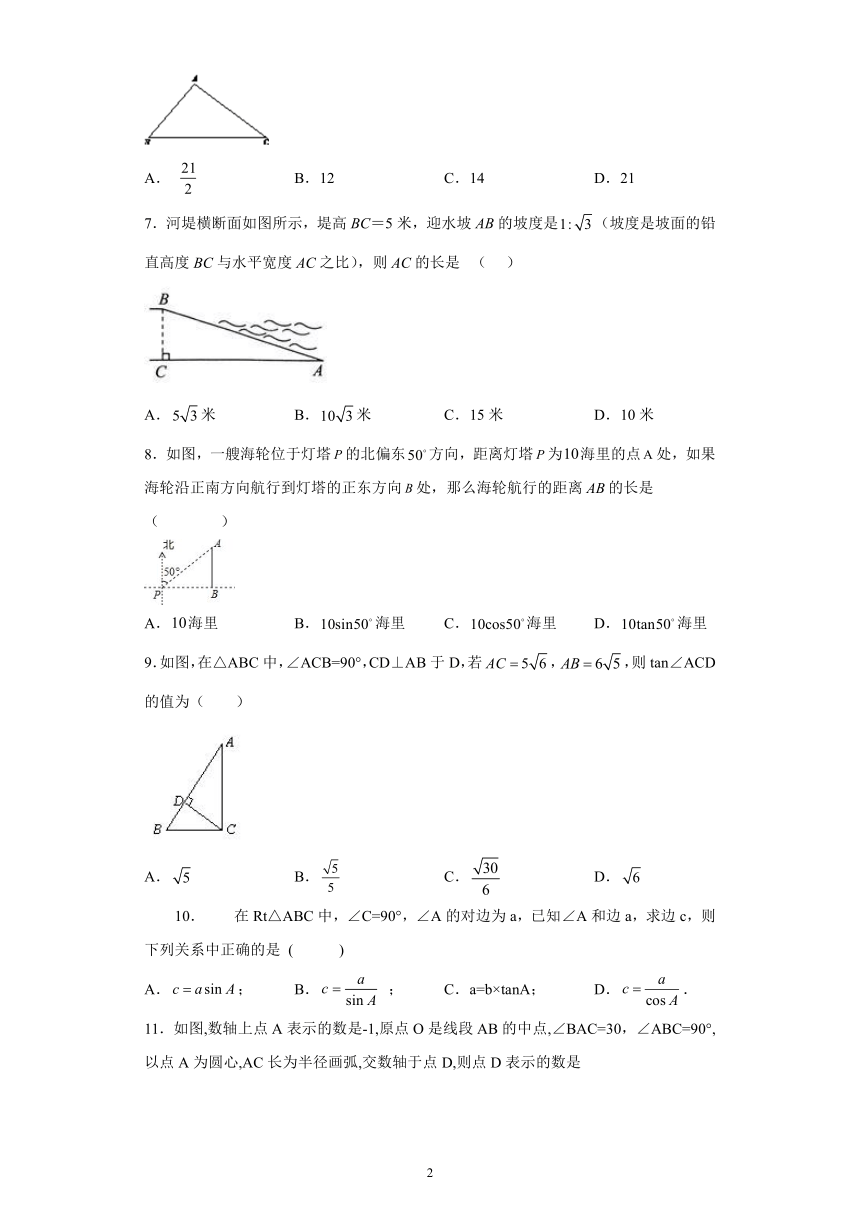
7.河堤横断面如图所示,堤高BC=5米,迎水坡AB的坡度是(坡度是坡面的铅直高度BC与水平宽度AC之比),则AC的长是 ( )
A.米 B.米 C.15米 D.10米
8.如图,一艘海轮位于灯塔的北偏东方向,距离灯塔为海里的点处,如果海轮沿正南方向航行到灯塔的正东方向处,那么海轮航行的距离的长是( )
A.海里 B.海里 C.海里 D.海里
9.如图,在△ABC中,∠ACB=90°,CD⊥AB于D,若,,则tan∠ACD的值为( )
A. B. C. D.
10. 在Rt△ABC中,∠C=90°,∠A的对边为a,已知∠A和边a,求边c,则下列关系中正确的是 ( )
A.; B. ; C.a=b×tanA; D..
11.如图,数轴上点A表示的数是-1,原点O是线段AB的中点,∠BAC=30,∠ABC=90°,以点A为圆心,AC长为半径画弧,交数轴于点D,则点D表示的数是
A. B. C. D.
12.cos60°-sin30°+tan45°的值为( )
A.2 B.-2 C.1 D.-1
13.计算:()﹣1+tan30° sin60°=( )
A.﹣ B.2 C. D.
二、填空题
14.如图所示,在△ABC中,∠ACB=90°,CD是AB边上的中线,AC=6,CD=5,则sin A等于________.
15.如图,在东西方向的海岸线上有A、B两个港口,甲货船从A港沿北偏东60°的方向以4海里/小时的速度出发,同时乙货船从B港沿西北方向出发,2小时后相遇在点P处,问乙货船每小时航行________海里.
16.在Rt△ABC中,∠C=90°,如果cosB=,BC=4,那么AB的长为________.
17.如图,等腰梯形ABCD中,AD∥BC,∠DBC=45°,翻折梯形ABCD,使点B重合于点D,折痕分别交边AB、BC于点F、E,若AD=2,BC=8.则(1)BE的长为_________. (2)∠CDE的正切值为________.
18.计算:= .
三、解答题
19.如图所示,在RtABC中,∠C=90°,∠B=30°,b=20,解这个直角三角形.
20.某无人机兴趣小组在操场上开展活动(如图),此时无人机在离地面30米的D处,无人机测得操控者A的俯角为37°,测得点C处的俯角为45°.又经过人工测量操控者A和教学楼BC距离为57米,求教学楼BC的高度.(注:点A,B,C,D都在同一平面上.参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
21.如图,在ABC中,AC=12cm,AB=16cm,sinA=.
(1)求AB边上的高CD;
(2)求ABC的面积S;
(3)求tanB.
22.如图,一艘海轮位于灯塔P的南偏东30°方向,距离灯塔100海里的A处,它计划沿正北方向航行,去往位于灯塔P的北偏东45°方向上的B处.
(1)问B处距离灯塔P有多远?(结果精确到0.1海里)
(2)假设有一圆形暗礁区域,它的圆心位于射线PB上,距离灯塔150海里的点O处.圆形暗礁区域的半径为60海里,进入这个区域,就有触礁的危险.请判断海轮到达B处是否有触礁的危险?如果海轮从B处继续向正北方向航行,是否有触礁的危险?并说明理由.(参考数据:≈1.414,≈1.732)
23.课堂上同学们借助两个直角三角形纸板进行探究,直角三角形纸板如图所示,分别为Rt△ABC和Rt△DEF,其中∠A=∠D=90°,AC=DE=2cm. 当边AC与DE重合,且边AB和DF在同一条直线上时:
(1)在下边的图形中,画出所有符合题意的图形;
(2)求BF的长.
参考答案
1.D
解:如图所示,过点C作CD⊥AB于D,∵ ∠BAC=120°,∴ ∠CAD=60°,
又∵ AC=2,∴ AD=1,CD=,
∴ BD=BA+AD=5,在Rt△BCD中,,
∴ .
故选:D.
2.D
解:如图所示,
在Rt△ACD中,AD=4,CD=3,
∴AC== =5
∴= = .
故选D.
3.D
根据题意得,≥0,解得≥0.4,α≈23.58°,
故选:D.
4.D
地毯长度等于两直角边长之和,高为2 m,宽为(m),
则地毯的总长至少为m
故选D.
5.C
解:在Rt△ABC中,由∠C=45°,得AB=BC,
在Rt△ABD中,
∵tan∠ADB=tan60°=,
∴BD=,
又∵CD=50m,
∴BC-BD=50,即AB- =50,
解得:AB≈118.
即摩天轮的高度AB约是118米.
故选C.
6.A
解:过点A作AD⊥BC,
∵△ABC中,cosB=,sinC=,AC=5,
∴cosB==,
∴∠B=45°,
∵sinC===,
∴AD=3,
∴CD==4,
∴BD=3,
则△ABC的面积是:×AD×BC=×3×(3+4)=.
故选A.
7.A
解:Rt△ABC中,BC=5米,tanA=1:;
∴AC=BC÷tanA=米.
故答案选:A.
8.C
解:如图,由题意可知∠NPA=50°,AP=10海里,∠ABP=90°.
∵AB∥NP,
∴∠A=∠NPA=50°.
在Rt△ABP中,∵∠ABP=90°,∠A=50°,AP=10海里,
∴AB=AP cos∠A=10cos50°海里.
故选C.
9.B
∵AB=6,AC=5,∴BC==,∵CD⊥AB,∴∠BCD+∠B=90°,∵∠A+∠B=90°,∴∠BCD=∠A,则tan∠BCD=tan∠A=,故答案选B.
10.B
在Rt△ABC中,∠C=90°,∠A的对边为a,
∴sinA=,
∴.
故选B.
11.D
∵点A表示-1,O是AB的中点,
∴OA=OB=1,
∴AB=2,
在Rt△ABC中,AC=,
∴AD=AC=,
∴OD=-1.
故选:D.
12.C
原式
故选:C.
13.C
()﹣1+tan30° sin60°
=2+
=2+
=,
故选C.
14.
解:∵CD是AB边上的中线,
∴CD=AD
∴AB=2CD=2×5=10
∴BC=
∵sin A=
15.2
过点作交于点,
∵甲货船从港沿北偏东的方向以海里/小时的速度出发,
∵乙货船从港沿西北方向出发,
∴乙货船每小时航行
故答案为.
16.6
解:Rt△ABC中,∠C=90°,cosB=,可知cosB=得到AB= ,又知BC=4,代入得到AB=
故填6.
17.BE=5; tan∠CDE=
(1)由题意得△BFE≌△DFE,
∴DE=BE.
又∵在△BDE中,∠DBE=45°,
∴∠BDE=∠DBE=45°,
∴∠BED=90°,即DE⊥BC.
∵在等腰梯形ABCD中,AD=2,BC=8,
过A作AG⊥BC于G,
∵四边形AGED是矩形.
∴AD=GE=2,AG=DE.
∵四边形ABCD是等腰梯形,
∴AB=CD,
∵∠AGB=∠DEC=90°
Rt△ABG和Rt△DCE中,
∴Rt△ABG≌Rt△DCE(HL),
∴BG=EC=3.
∴BE=5
(2)由(1)得DE=BE=5,
在△DEC中,∠DEC=90°,DE=5,EC=3,
∴tan∠CDE==
故答案为(1) BE=5; (2) tan∠CDE=
18..
原式=.
19.∠A=60°,,c=40
由∠C=90°知,∠A+∠B=90°,而∠B=30°,
∴∠A=90°-30°=60°,
,
∴,
∴c=40,
由勾股定理知,
∴,
解得:.
20.教学楼BC高约13米.
解:过点D作DE⊥AB于点E,过点C作CF⊥DE于点F.
则四边形BCFE是矩形,
由题意得,AB=57,DE=30,∠A=37°,∠DCF=45°.
在Rt△ADE中,∠AED=90°,
∴tan∠DAE=tan37°=≈0.75.
∴AE=40.
∵AB=57,
∴BE=17.
∵四边形BCFE是矩形,
∴CF=BE=17.
在Rt△DCF中,∠DFC=90°,
∴∠CDF=∠DCF=45°.
∴DF=CF=17.
∴BC=EF=30-17=13.
答:教学楼BC高约13米.
21.(1);(2);(3).
解:(1)如图,,,
;
(2),
;
(3)在中,,
,
.
22.(1)70.7海里;(2)有触礁的危险,理由见解析
(1)过点P作PD⊥AB于点D.
依题意可知,PA=100,∠APD=60°,∠BPD=45°.
∴∠A=30°.
∴PD=50.
在△PBD中,BD=PD=50,
∴PB=50≈70.7.
答:B处距离灯塔P约70.7海里.
(2)依题意知:OP=150,OB=150﹣50.
∴海轮到达B处没有触礁的危险.
过点O作OE⊥AB,交AB延长线于点E,
∵∠OBE=∠PBD=45°,
∴OE=OBsin∠OBE=(150﹣50)×=75﹣50≈56.07<60,
∴海轮从B处继续向正北方向航行,有触礁的危险.
23.(1)补全图形见解析;(2)BF=(+2)cm或BF=(-2)cm.
(1)补全图形如图:
情况Ⅰ:
情况Ⅱ:
(2)情况Ⅰ:
解:∵在Rt△ACF中,∠F=∠ACF=45°
∴AF=AC=2cm.
∵在Rt△ACB中,∠B=30°,
∴BC=4,AB=.
∴BF=(+2)cm.
情况Ⅱ:
解:∵在Rt△ACF中,∠F=∠ACF=45°
∴AF=AC=2cm.
∵在Rt△ACB中,∠B=30°,
∴BC=4,AB=.
∴BF=(-2)cm.
一、单选题
1.如图,在ABC中,∠A=120°,AB=4,AC=2,则sinB的值是( )
A. B. C. D.
2.如图,△ABC的顶点都在方格纸的格点上,那么的值为( )
A. B. C. D.
3.要使式子有意义,则α可以取下列数值中的(D)
A.17° B.19°
C.21° D.24°
4.如图所示,在高为2 m,坡角为30°的楼梯上铺地毯,则地毯的长度至少应为( ).
A.4 m B.6 m C.m D.
5.某校数学兴趣小组要测量摩天轮的高度.如图,他们在C处测得摩天轮的最高点A的仰角为45°,再往摩天轮的方向前进50 m至D处,测得最高点A的仰角为60°.问摩天轮的高度AB约是( )
(结果精确到1 米,参考数据:≈1.41,≈1.73)
A.120米 B.117米 C.118米 D.119米
6.如图,在△ABC中,cosB=,sinC=,AC=5,则△ABC的面积是( )
A. B.12 C.14 D.21
7.河堤横断面如图所示,堤高BC=5米,迎水坡AB的坡度是(坡度是坡面的铅直高度BC与水平宽度AC之比),则AC的长是 ( )
A.米 B.米 C.15米 D.10米
8.如图,一艘海轮位于灯塔的北偏东方向,距离灯塔为海里的点处,如果海轮沿正南方向航行到灯塔的正东方向处,那么海轮航行的距离的长是( )
A.海里 B.海里 C.海里 D.海里
9.如图,在△ABC中,∠ACB=90°,CD⊥AB于D,若,,则tan∠ACD的值为( )
A. B. C. D.
10. 在Rt△ABC中,∠C=90°,∠A的对边为a,已知∠A和边a,求边c,则下列关系中正确的是 ( )
A.; B. ; C.a=b×tanA; D..
11.如图,数轴上点A表示的数是-1,原点O是线段AB的中点,∠BAC=30,∠ABC=90°,以点A为圆心,AC长为半径画弧,交数轴于点D,则点D表示的数是
A. B. C. D.
12.cos60°-sin30°+tan45°的值为( )
A.2 B.-2 C.1 D.-1
13.计算:()﹣1+tan30° sin60°=( )
A.﹣ B.2 C. D.
二、填空题
14.如图所示,在△ABC中,∠ACB=90°,CD是AB边上的中线,AC=6,CD=5,则sin A等于________.
15.如图,在东西方向的海岸线上有A、B两个港口,甲货船从A港沿北偏东60°的方向以4海里/小时的速度出发,同时乙货船从B港沿西北方向出发,2小时后相遇在点P处,问乙货船每小时航行________海里.
16.在Rt△ABC中,∠C=90°,如果cosB=,BC=4,那么AB的长为________.
17.如图,等腰梯形ABCD中,AD∥BC,∠DBC=45°,翻折梯形ABCD,使点B重合于点D,折痕分别交边AB、BC于点F、E,若AD=2,BC=8.则(1)BE的长为_________. (2)∠CDE的正切值为________.
18.计算:= .
三、解答题
19.如图所示,在RtABC中,∠C=90°,∠B=30°,b=20,解这个直角三角形.
20.某无人机兴趣小组在操场上开展活动(如图),此时无人机在离地面30米的D处,无人机测得操控者A的俯角为37°,测得点C处的俯角为45°.又经过人工测量操控者A和教学楼BC距离为57米,求教学楼BC的高度.(注:点A,B,C,D都在同一平面上.参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
21.如图,在ABC中,AC=12cm,AB=16cm,sinA=.
(1)求AB边上的高CD;
(2)求ABC的面积S;
(3)求tanB.
22.如图,一艘海轮位于灯塔P的南偏东30°方向,距离灯塔100海里的A处,它计划沿正北方向航行,去往位于灯塔P的北偏东45°方向上的B处.
(1)问B处距离灯塔P有多远?(结果精确到0.1海里)
(2)假设有一圆形暗礁区域,它的圆心位于射线PB上,距离灯塔150海里的点O处.圆形暗礁区域的半径为60海里,进入这个区域,就有触礁的危险.请判断海轮到达B处是否有触礁的危险?如果海轮从B处继续向正北方向航行,是否有触礁的危险?并说明理由.(参考数据:≈1.414,≈1.732)
23.课堂上同学们借助两个直角三角形纸板进行探究,直角三角形纸板如图所示,分别为Rt△ABC和Rt△DEF,其中∠A=∠D=90°,AC=DE=2cm. 当边AC与DE重合,且边AB和DF在同一条直线上时:
(1)在下边的图形中,画出所有符合题意的图形;
(2)求BF的长.
参考答案
1.D
解:如图所示,过点C作CD⊥AB于D,∵ ∠BAC=120°,∴ ∠CAD=60°,
又∵ AC=2,∴ AD=1,CD=,
∴ BD=BA+AD=5,在Rt△BCD中,,
∴ .
故选:D.
2.D
解:如图所示,
在Rt△ACD中,AD=4,CD=3,
∴AC== =5
∴= = .
故选D.
3.D
根据题意得,≥0,解得≥0.4,α≈23.58°,
故选:D.
4.D
地毯长度等于两直角边长之和,高为2 m,宽为(m),
则地毯的总长至少为m
故选D.
5.C
解:在Rt△ABC中,由∠C=45°,得AB=BC,
在Rt△ABD中,
∵tan∠ADB=tan60°=,
∴BD=,
又∵CD=50m,
∴BC-BD=50,即AB- =50,
解得:AB≈118.
即摩天轮的高度AB约是118米.
故选C.
6.A
解:过点A作AD⊥BC,
∵△ABC中,cosB=,sinC=,AC=5,
∴cosB==,
∴∠B=45°,
∵sinC===,
∴AD=3,
∴CD==4,
∴BD=3,
则△ABC的面积是:×AD×BC=×3×(3+4)=.
故选A.
7.A
解:Rt△ABC中,BC=5米,tanA=1:;
∴AC=BC÷tanA=米.
故答案选:A.
8.C
解:如图,由题意可知∠NPA=50°,AP=10海里,∠ABP=90°.
∵AB∥NP,
∴∠A=∠NPA=50°.
在Rt△ABP中,∵∠ABP=90°,∠A=50°,AP=10海里,
∴AB=AP cos∠A=10cos50°海里.
故选C.
9.B
∵AB=6,AC=5,∴BC==,∵CD⊥AB,∴∠BCD+∠B=90°,∵∠A+∠B=90°,∴∠BCD=∠A,则tan∠BCD=tan∠A=,故答案选B.
10.B
在Rt△ABC中,∠C=90°,∠A的对边为a,
∴sinA=,
∴.
故选B.
11.D
∵点A表示-1,O是AB的中点,
∴OA=OB=1,
∴AB=2,
在Rt△ABC中,AC=,
∴AD=AC=,
∴OD=-1.
故选:D.
12.C
原式
故选:C.
13.C
()﹣1+tan30° sin60°
=2+
=2+
=,
故选C.
14.
解:∵CD是AB边上的中线,
∴CD=AD
∴AB=2CD=2×5=10
∴BC=
∵sin A=
15.2
过点作交于点,
∵甲货船从港沿北偏东的方向以海里/小时的速度出发,
∵乙货船从港沿西北方向出发,
∴乙货船每小时航行
故答案为.
16.6
解:Rt△ABC中,∠C=90°,cosB=,可知cosB=得到AB= ,又知BC=4,代入得到AB=
故填6.
17.BE=5; tan∠CDE=
(1)由题意得△BFE≌△DFE,
∴DE=BE.
又∵在△BDE中,∠DBE=45°,
∴∠BDE=∠DBE=45°,
∴∠BED=90°,即DE⊥BC.
∵在等腰梯形ABCD中,AD=2,BC=8,
过A作AG⊥BC于G,
∵四边形AGED是矩形.
∴AD=GE=2,AG=DE.
∵四边形ABCD是等腰梯形,
∴AB=CD,
∵∠AGB=∠DEC=90°
Rt△ABG和Rt△DCE中,
∴Rt△ABG≌Rt△DCE(HL),
∴BG=EC=3.
∴BE=5
(2)由(1)得DE=BE=5,
在△DEC中,∠DEC=90°,DE=5,EC=3,
∴tan∠CDE==
故答案为(1) BE=5; (2) tan∠CDE=
18..
原式=.
19.∠A=60°,,c=40
由∠C=90°知,∠A+∠B=90°,而∠B=30°,
∴∠A=90°-30°=60°,
,
∴,
∴c=40,
由勾股定理知,
∴,
解得:.
20.教学楼BC高约13米.
解:过点D作DE⊥AB于点E,过点C作CF⊥DE于点F.
则四边形BCFE是矩形,
由题意得,AB=57,DE=30,∠A=37°,∠DCF=45°.
在Rt△ADE中,∠AED=90°,
∴tan∠DAE=tan37°=≈0.75.
∴AE=40.
∵AB=57,
∴BE=17.
∵四边形BCFE是矩形,
∴CF=BE=17.
在Rt△DCF中,∠DFC=90°,
∴∠CDF=∠DCF=45°.
∴DF=CF=17.
∴BC=EF=30-17=13.
答:教学楼BC高约13米.
21.(1);(2);(3).
解:(1)如图,,,
;
(2),
;
(3)在中,,
,
.
22.(1)70.7海里;(2)有触礁的危险,理由见解析
(1)过点P作PD⊥AB于点D.
依题意可知,PA=100,∠APD=60°,∠BPD=45°.
∴∠A=30°.
∴PD=50.
在△PBD中,BD=PD=50,
∴PB=50≈70.7.
答:B处距离灯塔P约70.7海里.
(2)依题意知:OP=150,OB=150﹣50.
∴海轮到达B处没有触礁的危险.
过点O作OE⊥AB,交AB延长线于点E,
∵∠OBE=∠PBD=45°,
∴OE=OBsin∠OBE=(150﹣50)×=75﹣50≈56.07<60,
∴海轮从B处继续向正北方向航行,有触礁的危险.
23.(1)补全图形见解析;(2)BF=(+2)cm或BF=(-2)cm.
(1)补全图形如图:
情况Ⅰ:
情况Ⅱ:
(2)情况Ⅰ:
解:∵在Rt△ACF中,∠F=∠ACF=45°
∴AF=AC=2cm.
∵在Rt△ACB中,∠B=30°,
∴BC=4,AB=.
∴BF=(+2)cm.
情况Ⅱ:
解:∵在Rt△ACF中,∠F=∠ACF=45°
∴AF=AC=2cm.
∵在Rt△ACB中,∠B=30°,
∴BC=4,AB=.
∴BF=(-2)cm.
同课章节目录
- 第十八章 相似形
- 18.1 比例线段
- 18.2 黄金分割
- 18.3 平行线分三角形两边成比例
- 18.4 相似多边形
- 18.5 相似三角形的判定
- 18.6 相似三角形的性质
- 18.7 应用举例
- 第十九章 二次函数和反比例函数
- 19.1 二次函数
- 19.2 二次函数 y=ax2+bx+c(a≠0) 的图象
- 19.3 二次函数的性质
- 19.4 二次函数的应用
- 19.5 反比例函数
- 19.6 反比例函数的图象、性质和应用
- 第二十章 解直角三角形
- 20.1 锐角三角函数
- 20.2 30°、45°、60° 角的三角函数值
- 20.3 用科学计算器求锐角三角函数值
- 20.4 解直角三角形
- 20.5 测量与计算
- 第二十一章 圆(上)
- 21.1 圆的有关概念
- 21.2 过三点的圆
- 21.3 圆的对称性
- 21.4 圆周角
- 第二十二章 圆(下)
- 22.1 直线和圆的位置关系
- 22.2 圆的切线
- 22.3 正多边形的有关计算
