2021-2022学年人教版数学九年级上册24.4.1弧长及扇形面积课件(共19张PPT)
文档属性
| 名称 | 2021-2022学年人教版数学九年级上册24.4.1弧长及扇形面积课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 594.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-25 11:26:56 | ||
图片预览





文档简介
(共19张PPT)
第二十四章 圆
24.4 弧长和扇形面积
第1课时 弧长和扇形面积
1.经历探索弧长计算公式及扇形面积计算公式的过程,培养学生的探索能力.
2.了解弧长及扇形面积公式后,能用公式解决问题,训练学生的数学运用能力.
1.半径为R的圆,周长是多少?
C=2πR
2.圆的周长可以看作是多少度的圆心角
所对的弧?
360°
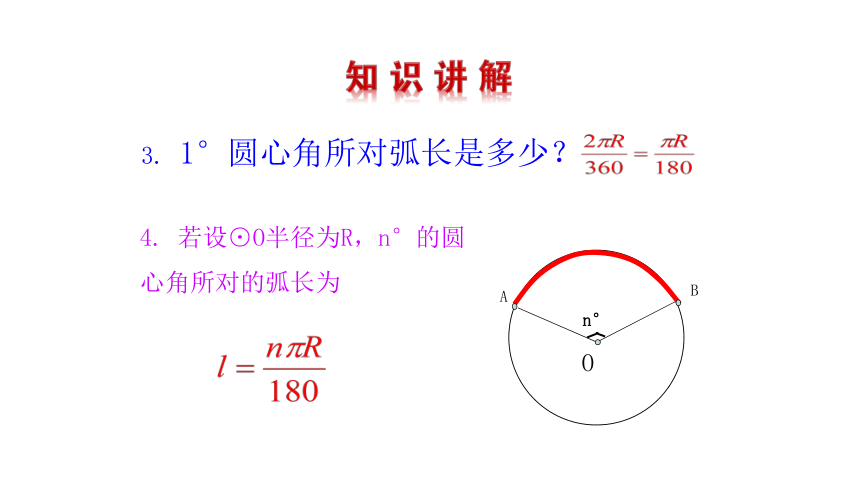
3. 1°圆心角所对弧长是多少?
n°
A
B
O
4. 若设⊙O半径为R,n°的圆心角所对的弧长为
若设扇子半径为30cm,120°的圆心角所对的弧长为 cm
20π
已知一条弧的半径为9,弧长为8 ,
那么这条弧所对的圆心角为_______.
160°
【跟踪训练】
由组成圆心角的两条半径和圆心角所对的弧围成的图形叫做扇形.
n°
o
A
B
O
A
B
O
1.半径为R的圆,面积是多少?
S=πR2
3.1°圆心角所对扇形面积是多少?
2.圆面可以看作是多少度的圆心角所对的扇形?
若设⊙O半径为R, n°的圆
心角所对的扇形面积为S,则
360°
1.已知扇形的圆心角为120°,半径为2,
则这个扇形的面积S扇形=____.
2.已知扇形面积为 ,圆心角为60°,
则这个扇形的半径R=____.
【跟踪训练】
3.已知半径为2cm的扇形,其弧长为 ,
则这个扇形的面积S扇形=____.
【跟踪训练】
A
B
O
O
比较扇形面积与弧长公式, 用弧长表示扇形面积:
A
B
C
D
O
1. 如图,已知□ABCD的对角线BD=4cm,将□ABCD绕其对称中心O旋转180°,则点D所转过的路径长为( C ) A.4π cm B.3π cm C.2π cm D.π cm
2.一块等边三角形的木板,边长为1,现将木板沿水平线翻滚
(如图),那么B点从开始至B2结束所走过的路径长度_______.
B
B1
B2
F'
B1
B
A
B
C
D
E
F
B2
●
3. 如图,在 中, 分别以
AC、BC为直径画半圆,则图中阴影部分的面积为 .(结果保留 )
C
A
B
【解析】
答案: 6 -4.
4. 如图,⊙O的半径等于1,弦AB和半径OC互相平分于点M.求扇形OACB的面积(结果保留π)
【解析】 ∵弦AB和半径OC互相平分∴OC⊥AB OM=MC=OC=OA在Rt△OAM中,∵OA=2OM, ∴∠A=30°又∵OA=OB ∴∠B=∠A=30°∴∠AOB=120°∴S扇形=
1.一块等边三角形的木板,边长为1,现将木板沿水平线翻滚(如图),那么B点从开始至B2结束所走过的路径长度________.
●
B
B1
B2
思考题
A
D
B
C
.E
2.如图, 矩形ABCD是一厚土墙截面,墙长15米,宽1米。在距D点5米处有一木桩E,木桩上拴一根绳子,绳子长7米,另一端拴着一只小狗,请问小狗的活动范围最大是多少?
思考题
1.弧长的计算公式l= 并运用公式进行计算.
2.扇形的面积公式S= 并运用公式进行计算.
3.弧长l及扇形的面积S之间的关系, .
通过本课时的学习,需要我们掌握:
谢谢聆听
第二十四章 圆
24.4 弧长和扇形面积
第1课时 弧长和扇形面积
1.经历探索弧长计算公式及扇形面积计算公式的过程,培养学生的探索能力.
2.了解弧长及扇形面积公式后,能用公式解决问题,训练学生的数学运用能力.
1.半径为R的圆,周长是多少?
C=2πR
2.圆的周长可以看作是多少度的圆心角
所对的弧?
360°
3. 1°圆心角所对弧长是多少?
n°
A
B
O
4. 若设⊙O半径为R,n°的圆心角所对的弧长为
若设扇子半径为30cm,120°的圆心角所对的弧长为 cm
20π
已知一条弧的半径为9,弧长为8 ,
那么这条弧所对的圆心角为_______.
160°
【跟踪训练】
由组成圆心角的两条半径和圆心角所对的弧围成的图形叫做扇形.
n°
o
A
B
O
A
B
O
1.半径为R的圆,面积是多少?
S=πR2
3.1°圆心角所对扇形面积是多少?
2.圆面可以看作是多少度的圆心角所对的扇形?
若设⊙O半径为R, n°的圆
心角所对的扇形面积为S,则
360°
1.已知扇形的圆心角为120°,半径为2,
则这个扇形的面积S扇形=____.
2.已知扇形面积为 ,圆心角为60°,
则这个扇形的半径R=____.
【跟踪训练】
3.已知半径为2cm的扇形,其弧长为 ,
则这个扇形的面积S扇形=____.
【跟踪训练】
A
B
O
O
比较扇形面积与弧长公式, 用弧长表示扇形面积:
A
B
C
D
O
1. 如图,已知□ABCD的对角线BD=4cm,将□ABCD绕其对称中心O旋转180°,则点D所转过的路径长为( C ) A.4π cm B.3π cm C.2π cm D.π cm
2.一块等边三角形的木板,边长为1,现将木板沿水平线翻滚
(如图),那么B点从开始至B2结束所走过的路径长度_______.
B
B1
B2
F'
B1
B
A
B
C
D
E
F
B2
●
3. 如图,在 中, 分别以
AC、BC为直径画半圆,则图中阴影部分的面积为 .(结果保留 )
C
A
B
【解析】
答案: 6 -4.
4. 如图,⊙O的半径等于1,弦AB和半径OC互相平分于点M.求扇形OACB的面积(结果保留π)
【解析】 ∵弦AB和半径OC互相平分∴OC⊥AB OM=MC=OC=OA在Rt△OAM中,∵OA=2OM, ∴∠A=30°又∵OA=OB ∴∠B=∠A=30°∴∠AOB=120°∴S扇形=
1.一块等边三角形的木板,边长为1,现将木板沿水平线翻滚(如图),那么B点从开始至B2结束所走过的路径长度________.
●
B
B1
B2
思考题
A
D
B
C
.E
2.如图, 矩形ABCD是一厚土墙截面,墙长15米,宽1米。在距D点5米处有一木桩E,木桩上拴一根绳子,绳子长7米,另一端拴着一只小狗,请问小狗的活动范围最大是多少?
思考题
1.弧长的计算公式l= 并运用公式进行计算.
2.扇形的面积公式S= 并运用公式进行计算.
3.弧长l及扇形的面积S之间的关系, .
通过本课时的学习,需要我们掌握:
谢谢聆听
同课章节目录
