2021-2022学年高二上学期物理人教版(2019)选择性必修第一册2.5 实验:用单摆测量重力加速度 同步练习题(word版含答案)
文档属性
| 名称 | 2021-2022学年高二上学期物理人教版(2019)选择性必修第一册2.5 实验:用单摆测量重力加速度 同步练习题(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 468.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-12-24 19:28:09 | ||
图片预览




文档简介
2.5 实验:用单摆测量重力加速度
一、单选题
1.在“用单摆测定重力加速度”的实验中,若测得的g值偏小,可能是因为( )
A.摆球的质量太大
B.测摆长时,将线长加小球直径作为摆长
C.测周期记录全振动次数时,将n次全振动误记为(n+1)次
D.摆球上端未固定牢固,摆动中出现松动,摆线变长
二、多选题
2.在用单摆测定重力加速度的实验中,为了减小测量误差,下列措施正确的有( )
A.对于相同半径的木球和铁球,选用铁球
B.单摆的摆角从原来的改变为
C.测量摆球振动周期时,选取最高点作为计时的起、终点位置
D.在测量单摆的周期时,防止出现“圆锥摆”
E.测量摆长时,单摆在悬挂状态下摆线长加上摆球的半径作为摆长
三、非选择题
3.图甲所示是演示振动图像的沙摆实验装置,沙摆可视为摆长L=1.0m的单摆,其摆动可看作简谐运动。实验中,细沙从摆动着的漏斗底部均匀漏出,用手沿与摆动方向垂直的方向匀速拉动纸板,漏在纸板上的细沙形成了图乙所示的粗细变化有规律的一条曲线。
(1)曲线之所以粗细不均匀,主要是因为沙摆摆动过程中_____(选填“位移”、“速度”或“加速度”)大小在变化;
(2)若图乙中AB间距离x=4.0m,当地重力加速度g=10m/s2,则纸板匀速运动的速度大小为____m/s。
4.在做“用单摆测定重力加速度”的实验过程中:
(1)小李同学用游标卡尺测得摆球的直径如图所示,则摆球直径d=________cm。
(2)小张同学实验时却不小心忘记测量小球的半径,但测量了两次摆线长和周期,第一次测得悬线长为L1,对应振动周期为T1;第二次测得悬线长为L2,对应单摆的振动周期为T2,根据以上测量数据也可导出重力加速度的表达式为_________________。
5.某同学在做“用单摆测定重力加速度”的实验。
(1)测摆长时测量结果如图所示(单摆摆线的另一端与刻度尺的零刻线对齐),摆长为________cm;然后用秒表记录了单摆振动50次所用的时间,如图所示,秒表读数为____________s;
(2)他测得的g值偏大,可能的原因是_______。
A.测摆长时摆线拉得过紧
B.摆线上端未牢固地系于悬点,振动中出现松动,使摆线长度增加了
C.开始计时时,秒表提前按下
D.实验中误将51次全振动次数计为50次
6.某实验小组利用如图甲所示的装置测量当地的重力加速度。
(1)为了使测量误差尽量小,下列说法中正确的是________;
A.组装单摆须选用密度和直径都较小的摆球
B.组装单摆须选用轻且不易伸长的细线
C.实验时须使摆球在同一竖直面内摆动
D.为了使单摆的周期大一些,应使摆线相距平衡位置有较大的角度
(2)该实验小组用20分度的游标卡尺测量小球的直径。某次测量的示数如图乙所示,读出小球直径为d=______cm;
(3)该同学用米尺测出悬线的长度为L,让小球在竖直平面内摆动。当小球经过最低点时开始计时,并计数为0,此后小球每经过最低点一次,依次计数为1、2、3……。当数到40时,停止计时,测得时间为t。改变悬线长度,多次测量,利用计算机作出了t2–L图线如图丙所示。根据图丙可以得出当地的重力加速度g=__________ m/s2。(取π2=9.86,结果保留3位有效数字)
7.用单摆测重力加速度时:
(1)摆球应采用直径较小,密度尽可能________的小球,摆线长度要在1米左右,用细而不易断的尼龙线.
(2)摆线偏离竖直方向的最大角度θ应________.
(3)要在摆球通过________位置时开始计时并计为零次,摆线每经过此位置两次才完成一次全振动,摆球应在________面内摆动,利用单摆测重力加速度的实验中,摆长的测量应在摆球自然下垂的状况下从悬点量至________.
(4)某同学在做“利用单摆测重力加速度”的实验中,先测得摆线长为L=97.50 cm;用50分度的游标卡尺(测量值可准确到0.02 mm)测得摆球直径为d=2.100 cm;然后用停表记录了单摆振动n=50次全振动所用的时间为t=99.9 s.则该摆摆长为________ cm,周期为________ s,计算重力加速度的表达式为________.
8.某同学利用如图所示的装置测量当地的重力加速度,实验步骤如下:
A.按装置图安装好实验装置;
B.用游标卡尺测量小球的直径d;
C.用米尺测量悬线的长度L;
D.让小球在竖直平面内小角度摆动。当小球经过最低点时开始计时,并计数为0,此后小球每经过最低点一次,依次计数1、2、3……。当数到20时,停止计时,测得时间为t;
E.多次改变悬线长度,对应每个悬线长度,都重复实验步骤C、D;
F.计算出每个悬线长度对应的t2;
G.以t2为纵坐标、L为横坐标,作出t2-L图线。
结合上述实验,完成下列任务:
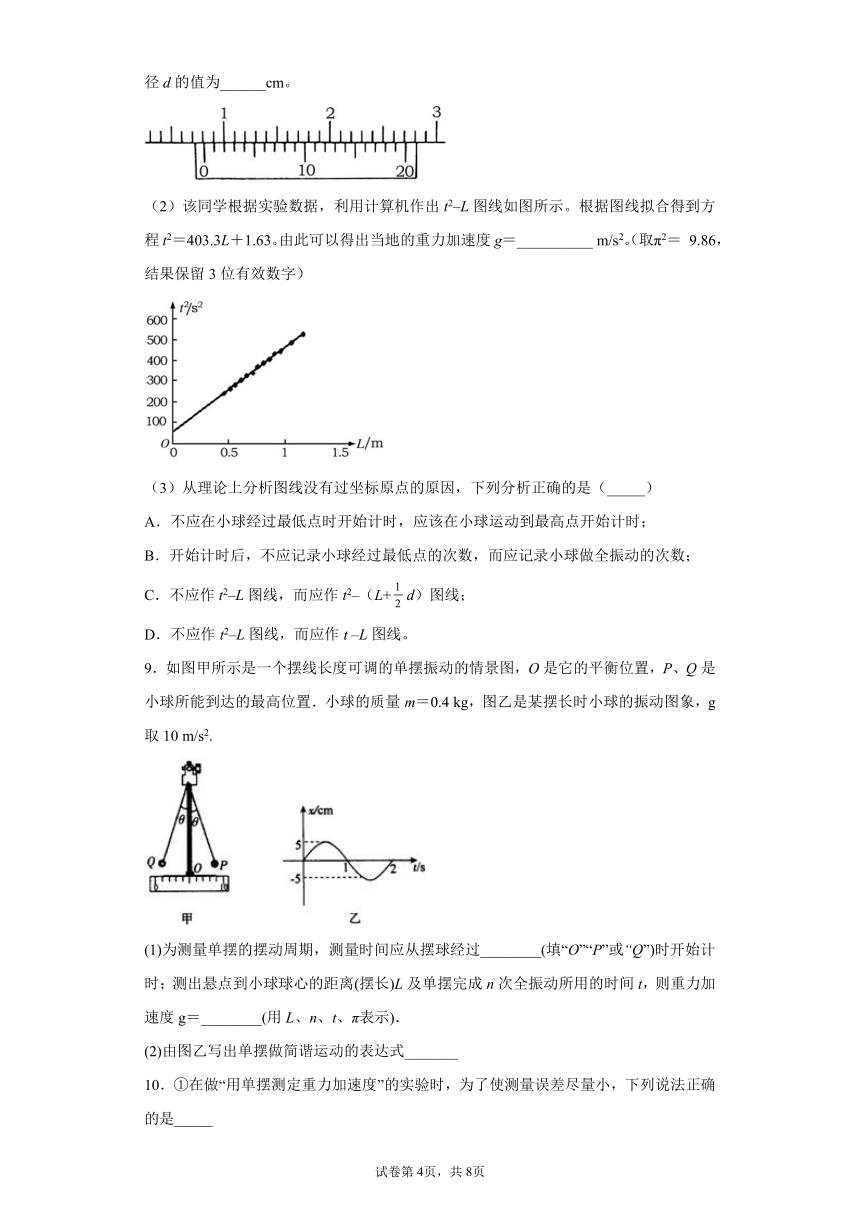
(1)用20分度的游标卡尺测量小球的直径。某次测量的示数如下图所示,读出小球直径d的值为______cm。
(2)该同学根据实验数据,利用计算机作出t2–L图线如图所示。根据图线拟合得到方程t2=403.3L+1.63。由此可以得出当地的重力加速度g=__________ m/s2。(取π2= 9.86,结果保留3位有效数字)
(3)从理论上分析图线没有过坐标原点的原因,下列分析正确的是(_____)
A.不应在小球经过最低点时开始计时,应该在小球运动到最高点开始计时;
B.开始计时后,不应记录小球经过最低点的次数,而应记录小球做全振动的次数;
C.不应作t2–L图线,而应作t2–(L+d)图线;
D.不应作t2–L图线,而应作t –L图线。
9.如图甲所示是一个摆线长度可调的单摆振动的情景图,O是它的平衡位置,P、Q是小球所能到达的最高位置.小球的质量m=0.4 kg,图乙是某摆长时小球的振动图象,g取10 m/s2.
(1)为测量单摆的摆动周期,测量时间应从摆球经过________(填“O”“P”或“Q”)时开始计时;测出悬点到小球球心的距离(摆长)L及单摆完成n次全振动所用的时间t,则重力加速度g=________(用L、n、t、π表示).
(2)由图乙写出单摆做简谐运动的表达式_______
10.①在做“用单摆测定重力加速度”的实验时,为了使测量误差尽量小,下列说法正确的是_____
A.须选用密度和直径都较小的摆球
B.须选用轻且不易伸长的细线
C.实验时须使摆球在同一竖直面内摆动
D.计时起、终点都应在摆球的最高点且不少于30次全振动的时间
②某同学在野外做“用单摆测定重力加速度”的实验时,由于没有合适的摆球,他找到了一块外形不规则的石块代替摆球,如上图所示。操作时,他用刻度尺测量摆线OM的长度L作为摆长,测出n次全振动的总时间由到周期T,求出重力加速度,这样得到的重力加速度的测量值比真实值_____(填“大”或“小”)。为了克服摆长无法准确测量的困难,该同学将摆线长度缩短为,重复上面的实验,得出周期,由此他得到了较精确的重力加速度值g=_____。
11.用单摆测定重力加速度的实验中:
(1)应选用下列器材中的(_________)
(A)半径 1cm 的木球 (B)半径 1cm 的实心钢球 (C)1m 左右的细线
(D)30cm 左右的细线 (E)秒表、三角板、米尺
(2)在做“用单摆测定重力加速度”的实验中,有人提出以下几点建议,其中对提高测量结果精确度有利的是(_________)
A.适当加长摆线
B.单摆偏离平衡位置的角度不能太大
C.质量相同、体积不同的摆球,选用体积较大的
D.当单摆经过平衡位置时开始计时,经过一次全振动后停止计时,用此时间间隔作为单摆振动的周期
(3)一端固定在房顶的一根细线垂到三楼窗沿下,某同学为了测量窗的上沿到房顶的高度, 在线的下端系了一小球,发现当小球静止时,细线保持竖直且恰好与窗子上沿接触。打开窗子,让小球在垂直于窗口的竖直平面内摆动,如图所示。
①为了测小球摆动的周期,他打开手机里的计时器,在某次小球从窗外向内运动到达最低点时数 1,同时开始计时,随后每次小球从外向内运动到最低点依次数 2、3、4…,数到 n 时, 手机上显示的时间为 t,则小球摆动的周期 T 为_______;
②该同学用钢卷尺测量出摆动中小球球心到窗上沿的距离,测得 50cm.又测出小球摆动的周期是 4.5s,当地的重力加速度为 9.8m/s2,则窗的上沿到房顶的高度约为_______.
12.(1)在“探究单摆周期与摆长的关系”的实验中,两位同学用游标卡尺测量小球的直径如图甲、乙所示.测量方法正确的是________(选填“甲”或“乙”).
(2)在探究影响单摆周期的因素时有如下操作,请判断是否恰当(填“是”或“否”).
①在摆球经过最低点时启动秒表计时:________;
②用秒表记录摆球一次全振动的时间作为周期:________.
(3)某同学利用单摆测定当地重力加速度,发现单摆静止时摆球重心在球心的正下方,他仍将从悬点到球心的距离当作摆长L,通过改变摆线的长度,测得6组L和对应的周期T,画出L-T2图线,然后在图线上选取A、B两个点,坐标如图所示.他采用恰当的数据处理方法,则计算重力加速度的表达式应为g=________.
13.某同学用实验的方法“探究单摆的周期与摆长的关系”。
⑴为测量摆线长,必须使单摆处于_____(选填字母代码)状态
A.水平拉直 B.自然悬垂 C.悬挂拉紧
⑵ 他用毫米刻度尺从悬点量到摆球的最高端的长度L0=98.80cm,然后分别用两种仪器甲、乙来测量摆球直径,操作如图,得到摆球的直径为d=2.266cm,此测量数据是选用了仪器_____(选填“甲”或“乙”)测量得到的;
⑶根据上述测量结果,结合误差分析,他得到的摆长L是_____cm(结果保留四位有效数字)
⑷他改变摆长后,测量6种不同摆长情况下单摆的周期,记录表格如下:
l/cm 40.00 50.00 80.00 90.00 100.00 120.00
T/s 1.26 1.42 1.79 1.90 2.00 2.20
T2/s2 1.59 2.02 3.20 3.61 4.00 4.84
以摆长l为横坐标,T2为纵坐标,作出T2-l图线___,并利用此图线求重力加速度值为_______m/s2(结果保留三位有效数字,42=39.44)
14.在“利用单摆测重力加速度”的实验中:
(1)测得摆线长l0,小球直径D,小球完成n次全振动的时间为t,则实验测得的重力加速度的表达式g=___
(2)实验中如果重力加速度的测量值偏大,其可能的原因是(_____)
A.把摆线的长度l0当成了摆长
B.摆线上端未牢固地固定于O点,振动中出现松动,使摆线变长
C.测量周期时,误将摆球(n-l)次全振动的时间t记成了n次全振动的时间
D.摆球的质量过大
(3)如图所示,停表读数为___s.
(4)同学因为粗心忘记测量摆球直径,实验中将悬点到小球下端的距离作为摆长l,测得多组周期T和l的数据,作出图象,如图所示.则该小球的直径是___cm (保留一位小数);实验测得当地重力加速度大小是___m/s2 (取三位有效数字).
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.D
【详解】
在“用单摆测定重力加速度”的实验中,根据
得
A.g值与摆球的质量无关,A错误;
B.测摆长时,将线长加小球直径作为摆长,使得偏大,则g值偏大,B错误;
C.测周期记录全振动次数时,将n次全振动误记为(n+1)次,使得g值偏大,C错误;
D.摆球上端未固定牢固,摆动中出现松动,摆线变长,使得测得的比实际值偏小,则g值偏小,D正确。
故选D。
2.ADE
【详解】
A.对于相同半径的木球和铁球,选择铁球可以忽略空气阻力以及悬线的重力,A正确;
B.单摆在摆角很小的情况下才做简谐运动,单摆的摆角不能太大,一般不超过,B错误;
C.为了减小测量周期时的误差,应取摆球通过的最低点作为计时的起、终点位置,C错误;
D.摆球做圆锥摆时周期表达式为
若用
算出重力加速度误差较大,为了减小测量误差,应防止出现“圆锥摆”,D正确;
E.测量摆长时,单摆在悬挂状态下摆线长加上摆球的半径作为摆长,E正确。
故选ADE。
3.速度 1
【详解】
沙摆漏沙速度一定,但是曲线不均匀,说明沙摆的速度在变化;
单摆的周期为
故纸板的速度为
4.2.030
【详解】
(1)游标卡尺的主尺读数为20mm,游标尺读数为0.05×6mm=0.30mm,则摆球的直径d=20.30mm=2.030cm
(2)设小球的半径为r,根据单摆的周期公式得
T1=2π
T2=2π
联立方程组解得
5.99.80 130.5 A
【详解】
(1)毫米刻度尺最小刻度为1mm,估读到0.1mm,则摆长等于99.80cm;秒表最小刻度为0.5s不估读,秒表的读数为
120s+10.5s=130.5s
(2)根据,解得
A.测摆线时摆线拉得过紧,测得摆长偏大,则测得重力加速度偏大,故A正确;
B.摆线上端未牢固地系于悬点,振动中出现松动,使摆线长度增加,则测得的摆长偏小,测得重力加速度偏小,故B错误;
C.开始计时时,秒表提前按下,测得周期偏大,则重力加速度偏小,故C错误;
D.实验中误将51次全振动次数计为50次,测得周期偏大,则重力加速度偏小,故D错误。
故选AC。
6.BC 0.810 9.80
【详解】
(1)A.组装单摆须选用密度较大且直径较小的摆球,选项A错误;
B.组装单摆须选用轻且不易伸长的细线,选项B正确;
C.实验时须使摆球在同一竖直面内摆动,选项C正确;
D.单摆的摆角不得超过5°,否则单摆的运动就不是简谐运动,选项D错误;
故选BC。
(2)小球直径为d=0.8cm+0.05mm×2=0.810cm;
(3)单摆的周期为
由
可得
由图像可知
解得
g=9.80m/s2
7.(1)大 (2)小于5 (3)平衡, 同一竖直, 摆球球心 (4)98.550, 1.998, g=2π2n2(2L+d)/t2
【解析】
试题分析:(1)用单摆测重力加速度时,由于存在空气阻力对实验的影响,为了减小这种影响,所以采用体积小密度大的小球,有突出主要因素忽略次要因素的物理思想,当重力远远大于空气阻力时,空气阻力就可以忽略,所以要用密度大的小球,减小直径的目的是为了减小与空气的接触面积.(2)当角度很小时,单摆运动可以看成是简谐运动,由单摆周期公式算出的周期与实际测定之之间的误差,随着偏角的增大而增大,所以偏角越小,误差就会越小,所以最大角度θ应小于.(3)本实验偶然误差主要来自于时间(单摆周期)的测量上,因此,要注意测准时间,从摆球通过平衡位置开始计时,为了防止振动是圆锥摆,要再竖直平面内摆动,摆长是悬线的长度和小球半径之和,所以摆线从悬点至摆球球心.(4)真正的摆长为cm,周期s.根据周期公式得出代入摆长和周期计算可得.
考点:本题考查了用单摆测定重力加速度的实验方法和原理
8.0.810cm 9.78m/s2 C
【详解】
(1)由图示游标卡尺可知,主尺示数是0.8cm,游标尺示数是2×0.05mm=0.10mm=0.010cm,游标卡尺示数即小球的直径d=0.8cm+0.010cm=0.810cm;
(2)由题意知,单摆的周期
由单摆周期公式得
由图像得到的方程为
t2=403.3L+1.63
则
解得
(3)单摆摆长等于摆线长度与摆球半径之和,把摆线长度作为单摆摆长,摆长小于实际摆长,t2-L图像不过原点,在纵轴上截距不为零,故C正确。
故选C。
9.O x=5sin (πt)(cm)
【解析】
【详解】
(1)为测量单摆的摆动周期,测量时间应从摆球经过O时开始计时,单摆的周期为
由单摆的周期为
联立解得
.
(2)由图知A=5cm,T=2s,则
单摆做简谐运动的表达式为
x=Asinωt=5sinπt (cm).
10.BC 小
【解析】
【详解】
(1) A、为减小空气阻力对实验的影响,从而减小实验误差,组装单摆须选用密度大而直径都较小的摆球,故A错误;
B、为减小实验误差,组装单摆须选用轻且不易伸长的细线,故B正确;
C、实验时须使摆球在同一竖直面内摆动,不能使单摆成为圆锥摆,故C正确;
D、测量时间应从单摆摆到最低点开始,因为最低位置摆球速度最大,相同的视觉距离误差,引起的时间误差较小,则周期测量比较准确,故D错误;
(2) 根据单摆的周期公式得:,该同学用OM的长L作为摆长,摆长偏小,根据上述表达式得知,g的测量值偏小,设摆线的结点到大理石质心的距离为r,则根据单摆的周期公式得:,而,联立解得:。
11.BCE AB 13.8m
【详解】
AB.单摆在摆动过程中.阻力要尽量小甚至忽略不计,所以摆球选钢球;故B正确,A错误;
CD.摆长不能过小,一般取1m左右.故、C正确,AD错误.
E.试验中要用到秒表测量周期,米尺测摆线的长度,三角板测摆球的直径,故E正确.
A.单摆的摆长越长,周期越大,适当加长摆长,便于测量周期,故A正确;
B.要减小空气阻力的影响,应选体积较小的摆球。故B错误;
C.单摆在摆角很小的情况下才做简谐运动,则单摆偏离平衡位置的角度不能太大,一般不超过5°.故C正确;
D.单摆周期较小,把一次全振动的时间作为周期,测量误差较大,应采用累积法,测多个周期的时间取平均值作为单摆的周期。故D错误;
从小球第1次通过图中的最低点开始计时,第n次通过B点用时t,故周期为:
小摆的周期为:
,
大摆周期为:
,
其中有
联立解得,
12.(1)乙 (2)否 否 (3)
【分析】
(1)用游标卡尺测量小球的直径,应将小球卡在外爪的刀口上.
(2)当摆球经过最低点(平衡位置)开始计时误差较小,以及用秒表测量大约30次全振动所需的时间,再求出周期.
(3)根据,知.根据图线的斜率,求出重力加速度g.
【详解】
(1)用游标卡尺测量小球的直径,应将小球卡在外爪的刀口上.故乙正确.
(2)当摆球经过最低点(平衡位置)开始计时误差较小,以及用秒表测量大约30次全振动所需的时间,再求出周期,单单测一次全振动所需的时间表示周期误差较大.
(3)根据,得:.则图线的斜率
根据图线得 ,所以
故本题答案为:(1)乙(2)①是,②否 (3).
点评:解决本题的关键掌握游标卡尺的操作方法,知道单摆的周期公式,以及知道影响单摆周期的因素.
13.B 甲 99.93 9.86(9.86±0.10)均可
【详解】
(1)测量摆线长,必须使单摆处于自然悬垂状态,水平拉直或拉紧都会增大测量的误差。
故选B;
(2)图甲是50分度的游标卡尺,最小分度是0.02mm,而螺旋测微器的最小分度是0.001mm,小球的读数是d=2.266cm=22.66mm;符合游标卡尺的读数,不符合螺旋测微器的读数的精确度.故此测量数据是选用了仪器甲;
(3)摆长
(4)以摆长l为横坐标,T2为纵坐标,作出T2-l图线如图
根据单摆的周期公式得
所以图线的斜率
由图可得
则
由于误差9.86(±0.10)m/s2均可。
14. C 99.8s 1.2 9.86
【解析】
【详解】
(1)单摆的周期,摆长,根据可得重力加速度的表达式
g=
(2)A.若把摆线的长度当成了摆长,计算时摆长将变短,根据重力加速度的表达式知,重力加速度的测量值将偏小;故A错误;
B.摆线上端未牢固地固定于O点,振动中出现松动,使摆长变大,则单摆的周期变大,而计算时仍采用原摆长l,由g=知,则重力加速度的测量值将偏小,故B错误;
C.测量周期时,误将摆球(n-1)次全振动的时间t记成了n次全振动的时间,则算得的周期变小,重力加速度的测量值将偏大;故C正确
D.摆球的质量过大不影响单摆的周期,则算得的重力加速度不受影响;故D错误.
(3)停表的长针是秒针,转一周是30s.因为机械表采用的齿轮传动,指针不可能停留在两小格之间,所以不能估读出比0.1 s更短的时间,位于表上部中间的小圆圈里面的短针是分针,表针走一周是15 min,每一小格为0.5 min.由图知,短针读数为1.5min,长针读数为9.8s,所以停表的读数为99.8s.
(4)由单摆的周期T=2可知
l=+
根据图象与纵轴的截距知=0.6cm,则该小球的直径D=1.2cm.
图象的斜率k=,实验测得当地重力加速度大小
g=42k=42m/s2=9.86m/s2答案第1页,共2页
答案第1页,共2页
一、单选题
1.在“用单摆测定重力加速度”的实验中,若测得的g值偏小,可能是因为( )
A.摆球的质量太大
B.测摆长时,将线长加小球直径作为摆长
C.测周期记录全振动次数时,将n次全振动误记为(n+1)次
D.摆球上端未固定牢固,摆动中出现松动,摆线变长
二、多选题
2.在用单摆测定重力加速度的实验中,为了减小测量误差,下列措施正确的有( )
A.对于相同半径的木球和铁球,选用铁球
B.单摆的摆角从原来的改变为
C.测量摆球振动周期时,选取最高点作为计时的起、终点位置
D.在测量单摆的周期时,防止出现“圆锥摆”
E.测量摆长时,单摆在悬挂状态下摆线长加上摆球的半径作为摆长
三、非选择题
3.图甲所示是演示振动图像的沙摆实验装置,沙摆可视为摆长L=1.0m的单摆,其摆动可看作简谐运动。实验中,细沙从摆动着的漏斗底部均匀漏出,用手沿与摆动方向垂直的方向匀速拉动纸板,漏在纸板上的细沙形成了图乙所示的粗细变化有规律的一条曲线。
(1)曲线之所以粗细不均匀,主要是因为沙摆摆动过程中_____(选填“位移”、“速度”或“加速度”)大小在变化;
(2)若图乙中AB间距离x=4.0m,当地重力加速度g=10m/s2,则纸板匀速运动的速度大小为____m/s。
4.在做“用单摆测定重力加速度”的实验过程中:
(1)小李同学用游标卡尺测得摆球的直径如图所示,则摆球直径d=________cm。
(2)小张同学实验时却不小心忘记测量小球的半径,但测量了两次摆线长和周期,第一次测得悬线长为L1,对应振动周期为T1;第二次测得悬线长为L2,对应单摆的振动周期为T2,根据以上测量数据也可导出重力加速度的表达式为_________________。
5.某同学在做“用单摆测定重力加速度”的实验。
(1)测摆长时测量结果如图所示(单摆摆线的另一端与刻度尺的零刻线对齐),摆长为________cm;然后用秒表记录了单摆振动50次所用的时间,如图所示,秒表读数为____________s;
(2)他测得的g值偏大,可能的原因是_______。
A.测摆长时摆线拉得过紧
B.摆线上端未牢固地系于悬点,振动中出现松动,使摆线长度增加了
C.开始计时时,秒表提前按下
D.实验中误将51次全振动次数计为50次
6.某实验小组利用如图甲所示的装置测量当地的重力加速度。
(1)为了使测量误差尽量小,下列说法中正确的是________;
A.组装单摆须选用密度和直径都较小的摆球
B.组装单摆须选用轻且不易伸长的细线
C.实验时须使摆球在同一竖直面内摆动
D.为了使单摆的周期大一些,应使摆线相距平衡位置有较大的角度
(2)该实验小组用20分度的游标卡尺测量小球的直径。某次测量的示数如图乙所示,读出小球直径为d=______cm;
(3)该同学用米尺测出悬线的长度为L,让小球在竖直平面内摆动。当小球经过最低点时开始计时,并计数为0,此后小球每经过最低点一次,依次计数为1、2、3……。当数到40时,停止计时,测得时间为t。改变悬线长度,多次测量,利用计算机作出了t2–L图线如图丙所示。根据图丙可以得出当地的重力加速度g=__________ m/s2。(取π2=9.86,结果保留3位有效数字)
7.用单摆测重力加速度时:
(1)摆球应采用直径较小,密度尽可能________的小球,摆线长度要在1米左右,用细而不易断的尼龙线.
(2)摆线偏离竖直方向的最大角度θ应________.
(3)要在摆球通过________位置时开始计时并计为零次,摆线每经过此位置两次才完成一次全振动,摆球应在________面内摆动,利用单摆测重力加速度的实验中,摆长的测量应在摆球自然下垂的状况下从悬点量至________.
(4)某同学在做“利用单摆测重力加速度”的实验中,先测得摆线长为L=97.50 cm;用50分度的游标卡尺(测量值可准确到0.02 mm)测得摆球直径为d=2.100 cm;然后用停表记录了单摆振动n=50次全振动所用的时间为t=99.9 s.则该摆摆长为________ cm,周期为________ s,计算重力加速度的表达式为________.
8.某同学利用如图所示的装置测量当地的重力加速度,实验步骤如下:
A.按装置图安装好实验装置;
B.用游标卡尺测量小球的直径d;
C.用米尺测量悬线的长度L;
D.让小球在竖直平面内小角度摆动。当小球经过最低点时开始计时,并计数为0,此后小球每经过最低点一次,依次计数1、2、3……。当数到20时,停止计时,测得时间为t;
E.多次改变悬线长度,对应每个悬线长度,都重复实验步骤C、D;
F.计算出每个悬线长度对应的t2;
G.以t2为纵坐标、L为横坐标,作出t2-L图线。
结合上述实验,完成下列任务:
(1)用20分度的游标卡尺测量小球的直径。某次测量的示数如下图所示,读出小球直径d的值为______cm。
(2)该同学根据实验数据,利用计算机作出t2–L图线如图所示。根据图线拟合得到方程t2=403.3L+1.63。由此可以得出当地的重力加速度g=__________ m/s2。(取π2= 9.86,结果保留3位有效数字)
(3)从理论上分析图线没有过坐标原点的原因,下列分析正确的是(_____)
A.不应在小球经过最低点时开始计时,应该在小球运动到最高点开始计时;
B.开始计时后,不应记录小球经过最低点的次数,而应记录小球做全振动的次数;
C.不应作t2–L图线,而应作t2–(L+d)图线;
D.不应作t2–L图线,而应作t –L图线。
9.如图甲所示是一个摆线长度可调的单摆振动的情景图,O是它的平衡位置,P、Q是小球所能到达的最高位置.小球的质量m=0.4 kg,图乙是某摆长时小球的振动图象,g取10 m/s2.
(1)为测量单摆的摆动周期,测量时间应从摆球经过________(填“O”“P”或“Q”)时开始计时;测出悬点到小球球心的距离(摆长)L及单摆完成n次全振动所用的时间t,则重力加速度g=________(用L、n、t、π表示).
(2)由图乙写出单摆做简谐运动的表达式_______
10.①在做“用单摆测定重力加速度”的实验时,为了使测量误差尽量小,下列说法正确的是_____
A.须选用密度和直径都较小的摆球
B.须选用轻且不易伸长的细线
C.实验时须使摆球在同一竖直面内摆动
D.计时起、终点都应在摆球的最高点且不少于30次全振动的时间
②某同学在野外做“用单摆测定重力加速度”的实验时,由于没有合适的摆球,他找到了一块外形不规则的石块代替摆球,如上图所示。操作时,他用刻度尺测量摆线OM的长度L作为摆长,测出n次全振动的总时间由到周期T,求出重力加速度,这样得到的重力加速度的测量值比真实值_____(填“大”或“小”)。为了克服摆长无法准确测量的困难,该同学将摆线长度缩短为,重复上面的实验,得出周期,由此他得到了较精确的重力加速度值g=_____。
11.用单摆测定重力加速度的实验中:
(1)应选用下列器材中的(_________)
(A)半径 1cm 的木球 (B)半径 1cm 的实心钢球 (C)1m 左右的细线
(D)30cm 左右的细线 (E)秒表、三角板、米尺
(2)在做“用单摆测定重力加速度”的实验中,有人提出以下几点建议,其中对提高测量结果精确度有利的是(_________)
A.适当加长摆线
B.单摆偏离平衡位置的角度不能太大
C.质量相同、体积不同的摆球,选用体积较大的
D.当单摆经过平衡位置时开始计时,经过一次全振动后停止计时,用此时间间隔作为单摆振动的周期
(3)一端固定在房顶的一根细线垂到三楼窗沿下,某同学为了测量窗的上沿到房顶的高度, 在线的下端系了一小球,发现当小球静止时,细线保持竖直且恰好与窗子上沿接触。打开窗子,让小球在垂直于窗口的竖直平面内摆动,如图所示。
①为了测小球摆动的周期,他打开手机里的计时器,在某次小球从窗外向内运动到达最低点时数 1,同时开始计时,随后每次小球从外向内运动到最低点依次数 2、3、4…,数到 n 时, 手机上显示的时间为 t,则小球摆动的周期 T 为_______;
②该同学用钢卷尺测量出摆动中小球球心到窗上沿的距离,测得 50cm.又测出小球摆动的周期是 4.5s,当地的重力加速度为 9.8m/s2,则窗的上沿到房顶的高度约为_______.
12.(1)在“探究单摆周期与摆长的关系”的实验中,两位同学用游标卡尺测量小球的直径如图甲、乙所示.测量方法正确的是________(选填“甲”或“乙”).
(2)在探究影响单摆周期的因素时有如下操作,请判断是否恰当(填“是”或“否”).
①在摆球经过最低点时启动秒表计时:________;
②用秒表记录摆球一次全振动的时间作为周期:________.
(3)某同学利用单摆测定当地重力加速度,发现单摆静止时摆球重心在球心的正下方,他仍将从悬点到球心的距离当作摆长L,通过改变摆线的长度,测得6组L和对应的周期T,画出L-T2图线,然后在图线上选取A、B两个点,坐标如图所示.他采用恰当的数据处理方法,则计算重力加速度的表达式应为g=________.
13.某同学用实验的方法“探究单摆的周期与摆长的关系”。
⑴为测量摆线长,必须使单摆处于_____(选填字母代码)状态
A.水平拉直 B.自然悬垂 C.悬挂拉紧
⑵ 他用毫米刻度尺从悬点量到摆球的最高端的长度L0=98.80cm,然后分别用两种仪器甲、乙来测量摆球直径,操作如图,得到摆球的直径为d=2.266cm,此测量数据是选用了仪器_____(选填“甲”或“乙”)测量得到的;
⑶根据上述测量结果,结合误差分析,他得到的摆长L是_____cm(结果保留四位有效数字)
⑷他改变摆长后,测量6种不同摆长情况下单摆的周期,记录表格如下:
l/cm 40.00 50.00 80.00 90.00 100.00 120.00
T/s 1.26 1.42 1.79 1.90 2.00 2.20
T2/s2 1.59 2.02 3.20 3.61 4.00 4.84
以摆长l为横坐标,T2为纵坐标,作出T2-l图线___,并利用此图线求重力加速度值为_______m/s2(结果保留三位有效数字,42=39.44)
14.在“利用单摆测重力加速度”的实验中:
(1)测得摆线长l0,小球直径D,小球完成n次全振动的时间为t,则实验测得的重力加速度的表达式g=___
(2)实验中如果重力加速度的测量值偏大,其可能的原因是(_____)
A.把摆线的长度l0当成了摆长
B.摆线上端未牢固地固定于O点,振动中出现松动,使摆线变长
C.测量周期时,误将摆球(n-l)次全振动的时间t记成了n次全振动的时间
D.摆球的质量过大
(3)如图所示,停表读数为___s.
(4)同学因为粗心忘记测量摆球直径,实验中将悬点到小球下端的距离作为摆长l,测得多组周期T和l的数据,作出图象,如图所示.则该小球的直径是___cm (保留一位小数);实验测得当地重力加速度大小是___m/s2 (取三位有效数字).
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.D
【详解】
在“用单摆测定重力加速度”的实验中,根据
得
A.g值与摆球的质量无关,A错误;
B.测摆长时,将线长加小球直径作为摆长,使得偏大,则g值偏大,B错误;
C.测周期记录全振动次数时,将n次全振动误记为(n+1)次,使得g值偏大,C错误;
D.摆球上端未固定牢固,摆动中出现松动,摆线变长,使得测得的比实际值偏小,则g值偏小,D正确。
故选D。
2.ADE
【详解】
A.对于相同半径的木球和铁球,选择铁球可以忽略空气阻力以及悬线的重力,A正确;
B.单摆在摆角很小的情况下才做简谐运动,单摆的摆角不能太大,一般不超过,B错误;
C.为了减小测量周期时的误差,应取摆球通过的最低点作为计时的起、终点位置,C错误;
D.摆球做圆锥摆时周期表达式为
若用
算出重力加速度误差较大,为了减小测量误差,应防止出现“圆锥摆”,D正确;
E.测量摆长时,单摆在悬挂状态下摆线长加上摆球的半径作为摆长,E正确。
故选ADE。
3.速度 1
【详解】
沙摆漏沙速度一定,但是曲线不均匀,说明沙摆的速度在变化;
单摆的周期为
故纸板的速度为
4.2.030
【详解】
(1)游标卡尺的主尺读数为20mm,游标尺读数为0.05×6mm=0.30mm,则摆球的直径d=20.30mm=2.030cm
(2)设小球的半径为r,根据单摆的周期公式得
T1=2π
T2=2π
联立方程组解得
5.99.80 130.5 A
【详解】
(1)毫米刻度尺最小刻度为1mm,估读到0.1mm,则摆长等于99.80cm;秒表最小刻度为0.5s不估读,秒表的读数为
120s+10.5s=130.5s
(2)根据,解得
A.测摆线时摆线拉得过紧,测得摆长偏大,则测得重力加速度偏大,故A正确;
B.摆线上端未牢固地系于悬点,振动中出现松动,使摆线长度增加,则测得的摆长偏小,测得重力加速度偏小,故B错误;
C.开始计时时,秒表提前按下,测得周期偏大,则重力加速度偏小,故C错误;
D.实验中误将51次全振动次数计为50次,测得周期偏大,则重力加速度偏小,故D错误。
故选AC。
6.BC 0.810 9.80
【详解】
(1)A.组装单摆须选用密度较大且直径较小的摆球,选项A错误;
B.组装单摆须选用轻且不易伸长的细线,选项B正确;
C.实验时须使摆球在同一竖直面内摆动,选项C正确;
D.单摆的摆角不得超过5°,否则单摆的运动就不是简谐运动,选项D错误;
故选BC。
(2)小球直径为d=0.8cm+0.05mm×2=0.810cm;
(3)单摆的周期为
由
可得
由图像可知
解得
g=9.80m/s2
7.(1)大 (2)小于5 (3)平衡, 同一竖直, 摆球球心 (4)98.550, 1.998, g=2π2n2(2L+d)/t2
【解析】
试题分析:(1)用单摆测重力加速度时,由于存在空气阻力对实验的影响,为了减小这种影响,所以采用体积小密度大的小球,有突出主要因素忽略次要因素的物理思想,当重力远远大于空气阻力时,空气阻力就可以忽略,所以要用密度大的小球,减小直径的目的是为了减小与空气的接触面积.(2)当角度很小时,单摆运动可以看成是简谐运动,由单摆周期公式算出的周期与实际测定之之间的误差,随着偏角的增大而增大,所以偏角越小,误差就会越小,所以最大角度θ应小于.(3)本实验偶然误差主要来自于时间(单摆周期)的测量上,因此,要注意测准时间,从摆球通过平衡位置开始计时,为了防止振动是圆锥摆,要再竖直平面内摆动,摆长是悬线的长度和小球半径之和,所以摆线从悬点至摆球球心.(4)真正的摆长为cm,周期s.根据周期公式得出代入摆长和周期计算可得.
考点:本题考查了用单摆测定重力加速度的实验方法和原理
8.0.810cm 9.78m/s2 C
【详解】
(1)由图示游标卡尺可知,主尺示数是0.8cm,游标尺示数是2×0.05mm=0.10mm=0.010cm,游标卡尺示数即小球的直径d=0.8cm+0.010cm=0.810cm;
(2)由题意知,单摆的周期
由单摆周期公式得
由图像得到的方程为
t2=403.3L+1.63
则
解得
(3)单摆摆长等于摆线长度与摆球半径之和,把摆线长度作为单摆摆长,摆长小于实际摆长,t2-L图像不过原点,在纵轴上截距不为零,故C正确。
故选C。
9.O x=5sin (πt)(cm)
【解析】
【详解】
(1)为测量单摆的摆动周期,测量时间应从摆球经过O时开始计时,单摆的周期为
由单摆的周期为
联立解得
.
(2)由图知A=5cm,T=2s,则
单摆做简谐运动的表达式为
x=Asinωt=5sinπt (cm).
10.BC 小
【解析】
【详解】
(1) A、为减小空气阻力对实验的影响,从而减小实验误差,组装单摆须选用密度大而直径都较小的摆球,故A错误;
B、为减小实验误差,组装单摆须选用轻且不易伸长的细线,故B正确;
C、实验时须使摆球在同一竖直面内摆动,不能使单摆成为圆锥摆,故C正确;
D、测量时间应从单摆摆到最低点开始,因为最低位置摆球速度最大,相同的视觉距离误差,引起的时间误差较小,则周期测量比较准确,故D错误;
(2) 根据单摆的周期公式得:,该同学用OM的长L作为摆长,摆长偏小,根据上述表达式得知,g的测量值偏小,设摆线的结点到大理石质心的距离为r,则根据单摆的周期公式得:,而,联立解得:。
11.BCE AB 13.8m
【详解】
AB.单摆在摆动过程中.阻力要尽量小甚至忽略不计,所以摆球选钢球;故B正确,A错误;
CD.摆长不能过小,一般取1m左右.故、C正确,AD错误.
E.试验中要用到秒表测量周期,米尺测摆线的长度,三角板测摆球的直径,故E正确.
A.单摆的摆长越长,周期越大,适当加长摆长,便于测量周期,故A正确;
B.要减小空气阻力的影响,应选体积较小的摆球。故B错误;
C.单摆在摆角很小的情况下才做简谐运动,则单摆偏离平衡位置的角度不能太大,一般不超过5°.故C正确;
D.单摆周期较小,把一次全振动的时间作为周期,测量误差较大,应采用累积法,测多个周期的时间取平均值作为单摆的周期。故D错误;
从小球第1次通过图中的最低点开始计时,第n次通过B点用时t,故周期为:
小摆的周期为:
,
大摆周期为:
,
其中有
联立解得,
12.(1)乙 (2)否 否 (3)
【分析】
(1)用游标卡尺测量小球的直径,应将小球卡在外爪的刀口上.
(2)当摆球经过最低点(平衡位置)开始计时误差较小,以及用秒表测量大约30次全振动所需的时间,再求出周期.
(3)根据,知.根据图线的斜率,求出重力加速度g.
【详解】
(1)用游标卡尺测量小球的直径,应将小球卡在外爪的刀口上.故乙正确.
(2)当摆球经过最低点(平衡位置)开始计时误差较小,以及用秒表测量大约30次全振动所需的时间,再求出周期,单单测一次全振动所需的时间表示周期误差较大.
(3)根据,得:.则图线的斜率
根据图线得 ,所以
故本题答案为:(1)乙(2)①是,②否 (3).
点评:解决本题的关键掌握游标卡尺的操作方法,知道单摆的周期公式,以及知道影响单摆周期的因素.
13.B 甲 99.93 9.86(9.86±0.10)均可
【详解】
(1)测量摆线长,必须使单摆处于自然悬垂状态,水平拉直或拉紧都会增大测量的误差。
故选B;
(2)图甲是50分度的游标卡尺,最小分度是0.02mm,而螺旋测微器的最小分度是0.001mm,小球的读数是d=2.266cm=22.66mm;符合游标卡尺的读数,不符合螺旋测微器的读数的精确度.故此测量数据是选用了仪器甲;
(3)摆长
(4)以摆长l为横坐标,T2为纵坐标,作出T2-l图线如图
根据单摆的周期公式得
所以图线的斜率
由图可得
则
由于误差9.86(±0.10)m/s2均可。
14. C 99.8s 1.2 9.86
【解析】
【详解】
(1)单摆的周期,摆长,根据可得重力加速度的表达式
g=
(2)A.若把摆线的长度当成了摆长,计算时摆长将变短,根据重力加速度的表达式知,重力加速度的测量值将偏小;故A错误;
B.摆线上端未牢固地固定于O点,振动中出现松动,使摆长变大,则单摆的周期变大,而计算时仍采用原摆长l,由g=知,则重力加速度的测量值将偏小,故B错误;
C.测量周期时,误将摆球(n-1)次全振动的时间t记成了n次全振动的时间,则算得的周期变小,重力加速度的测量值将偏大;故C正确
D.摆球的质量过大不影响单摆的周期,则算得的重力加速度不受影响;故D错误.
(3)停表的长针是秒针,转一周是30s.因为机械表采用的齿轮传动,指针不可能停留在两小格之间,所以不能估读出比0.1 s更短的时间,位于表上部中间的小圆圈里面的短针是分针,表针走一周是15 min,每一小格为0.5 min.由图知,短针读数为1.5min,长针读数为9.8s,所以停表的读数为99.8s.
(4)由单摆的周期T=2可知
l=+
根据图象与纵轴的截距知=0.6cm,则该小球的直径D=1.2cm.
图象的斜率k=,实验测得当地重力加速度大小
g=42k=42m/s2=9.86m/s2答案第1页,共2页
答案第1页,共2页
