2021-2022人教版(2019)高中数学选择性必修第三册6.3.2二项式系数的性质 课件(23张ppt)
文档属性
| 名称 | 2021-2022人教版(2019)高中数学选择性必修第三册6.3.2二项式系数的性质 课件(23张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-25 10:41:02 | ||
图片预览







文档简介
(共23张PPT)
第六章 记数原理
6.3.2二项式系数的性质
复习引入
请同学回顾二项式的展开式及通项是什么?
请同学回顾二项式系数与系数的区别?
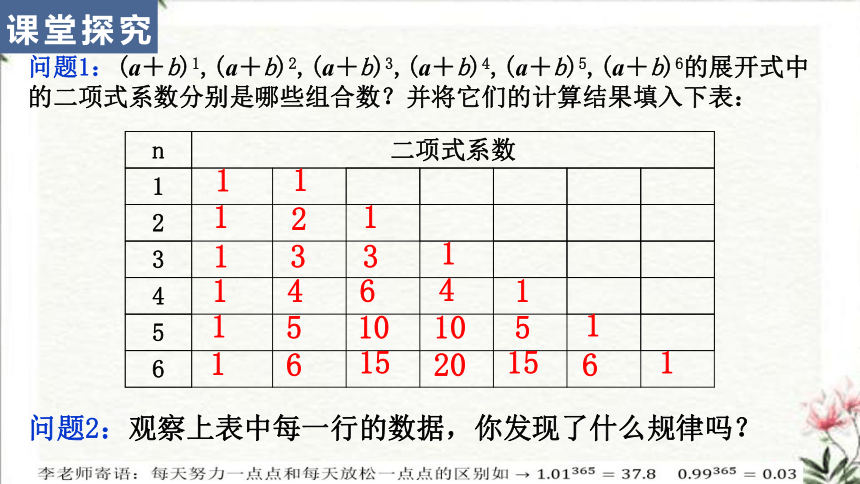
问题1:(a+b)1,(a+b)2,(a+b)3,(a+b)4,(a+b)5,(a+b)6的展开式中的二项式系数分别是哪些组合数?并将它们的计算结果填入下表:
6
5
4
3
2
1
二项式系数
n
1
1
1
1
2
1
1
3
3
1
1
4
6
4
1
1
5
10
10
5
1
1
6
15
15
20
6
问题2:观察上表中每一行的数据,你发现了什么规律吗?
课堂探究
1 4 6 4 1
1 1
1 2 1
1 3 3 1
1 5 10 10 5 1
1 6 15 20 15 6 1
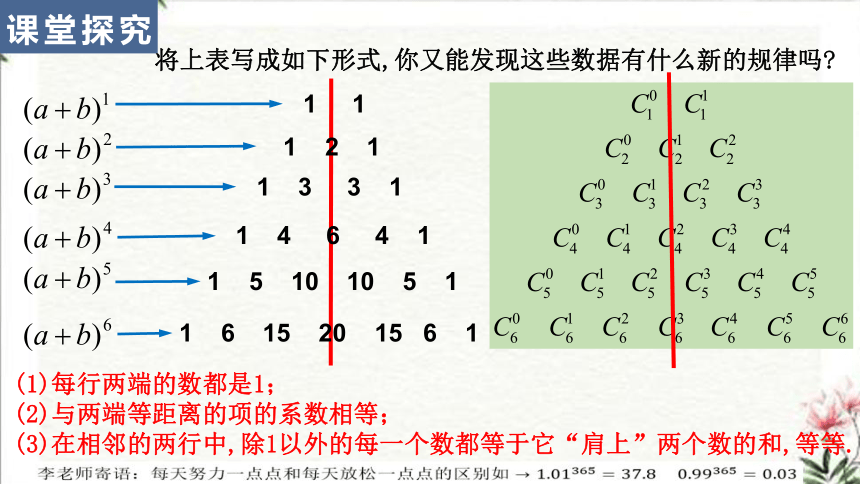
将上表写成如下形式,你又能发现这些数据有什么新的规律吗
(1)每行两端的数都是1;
(2)与两端等距离的项的系数相等;
(3)在相邻的两行中,除1以外的每一个数都等于它“肩上”两个数的和,等等.
课堂探究
问题:一般地,函数 ,r∈{0,1,2,…,n}的图象是什么? 它具有怎样的对称性?
课堂探究
问题:对给定的正整数n,设函数 ,
r∈{0,1,2,…,n},定义域是什么?
对于确定的n,我们还可以画出它的图象,例如,当n=6时,其图象是右图中的7个孤立点.
课堂探究
问题:一般地,函数 , r∈{0,1,2,…,n}的图象是什么? 它具有怎样的对称性?
n+1个孤立的点,关于直线 对称
课堂探究
二项式系数是逐渐增大的,
由对称性可知它的后半部分是逐渐减小的,即先增后减,
所以在中间项取得最大值.
所以,当 时,
课堂探究
问题:当n分别为偶数和奇数时,第几项的二项式系数最大?
∵二项展开式共有n+1项,
∴当n为偶数时,正中间一项的二项式系数 最大;
当n为奇数时,中间两项的二项式系数 相等,
且同时取得最大值
课堂探究
如何证明
在二项式定理中,a,b可以任意取值,当a=b=1时即可证明
课堂探究
又如何求(a+b)n的展开式中求,
奇数项的二项式系数的和
偶数项的二项式系数的和
提示:
课堂探究
例题解析
例题解析
例题解析
例题解析
练习巩固
例题解析
例题解析
例题解析
练习巩固
练习巩固
课堂小结
你收获了什么?
作业1:书本练习
作业2:报纸
作业3:
作业布置
第六章 记数原理
6.3.2二项式系数的性质
复习引入
请同学回顾二项式的展开式及通项是什么?
请同学回顾二项式系数与系数的区别?
问题1:(a+b)1,(a+b)2,(a+b)3,(a+b)4,(a+b)5,(a+b)6的展开式中的二项式系数分别是哪些组合数?并将它们的计算结果填入下表:
6
5
4
3
2
1
二项式系数
n
1
1
1
1
2
1
1
3
3
1
1
4
6
4
1
1
5
10
10
5
1
1
6
15
15
20
6
问题2:观察上表中每一行的数据,你发现了什么规律吗?
课堂探究
1 4 6 4 1
1 1
1 2 1
1 3 3 1
1 5 10 10 5 1
1 6 15 20 15 6 1
将上表写成如下形式,你又能发现这些数据有什么新的规律吗
(1)每行两端的数都是1;
(2)与两端等距离的项的系数相等;
(3)在相邻的两行中,除1以外的每一个数都等于它“肩上”两个数的和,等等.
课堂探究
问题:一般地,函数 ,r∈{0,1,2,…,n}的图象是什么? 它具有怎样的对称性?
课堂探究
问题:对给定的正整数n,设函数 ,
r∈{0,1,2,…,n},定义域是什么?
对于确定的n,我们还可以画出它的图象,例如,当n=6时,其图象是右图中的7个孤立点.
课堂探究
问题:一般地,函数 , r∈{0,1,2,…,n}的图象是什么? 它具有怎样的对称性?
n+1个孤立的点,关于直线 对称
课堂探究
二项式系数是逐渐增大的,
由对称性可知它的后半部分是逐渐减小的,即先增后减,
所以在中间项取得最大值.
所以,当 时,
课堂探究
问题:当n分别为偶数和奇数时,第几项的二项式系数最大?
∵二项展开式共有n+1项,
∴当n为偶数时,正中间一项的二项式系数 最大;
当n为奇数时,中间两项的二项式系数 相等,
且同时取得最大值
课堂探究
如何证明
在二项式定理中,a,b可以任意取值,当a=b=1时即可证明
课堂探究
又如何求(a+b)n的展开式中求,
奇数项的二项式系数的和
偶数项的二项式系数的和
提示:
课堂探究
例题解析
例题解析
例题解析
例题解析
练习巩固
例题解析
例题解析
例题解析
练习巩固
练习巩固
课堂小结
你收获了什么?
作业1:书本练习
作业2:报纸
作业3:
作业布置
