沪科版数学八年级上册 12.2 一元一次函数的图像和性质 课件(共26张PPT)
文档属性
| 名称 | 沪科版数学八年级上册 12.2 一元一次函数的图像和性质 课件(共26张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-25 10:37:00 | ||
图片预览




文档简介
(共26张PPT)
教学目标:
[1]了解正比例函数及一次函数图象的有关性质;体会一次函数的图象的位置关系。
[2]会用简单方法画一次函数的图象;
[3]培养学生数形结合的意识和能力。
*
(1)列表
(2)描点
(3)连线
2、画函数图象的一般步骤:
1.什么是一次函数?什么是正比例函数?
如果y=kx+b(k,b是常数,k≠0),那么y叫做x的一次函数。特别的,当b=0时,y=kx+b就成为y=kx,这时,y叫做x的正比例函数。
*
这节课我们要借助函数图象研究一次函数的性质.
我们先来看下面的问题:
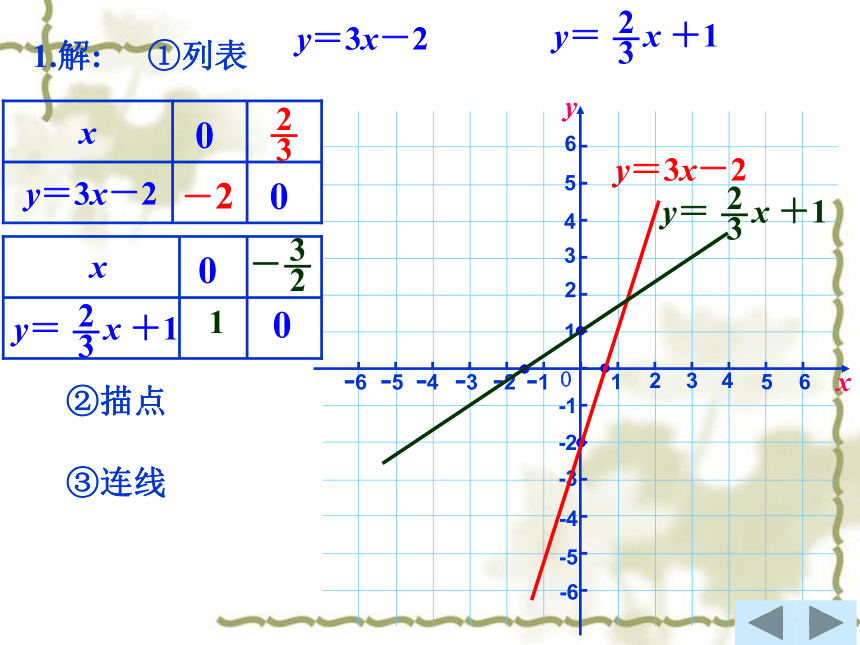
1.在同一直角坐标系中画出下列函数的图像:
y=3x-2
2
3
y= x +1
和
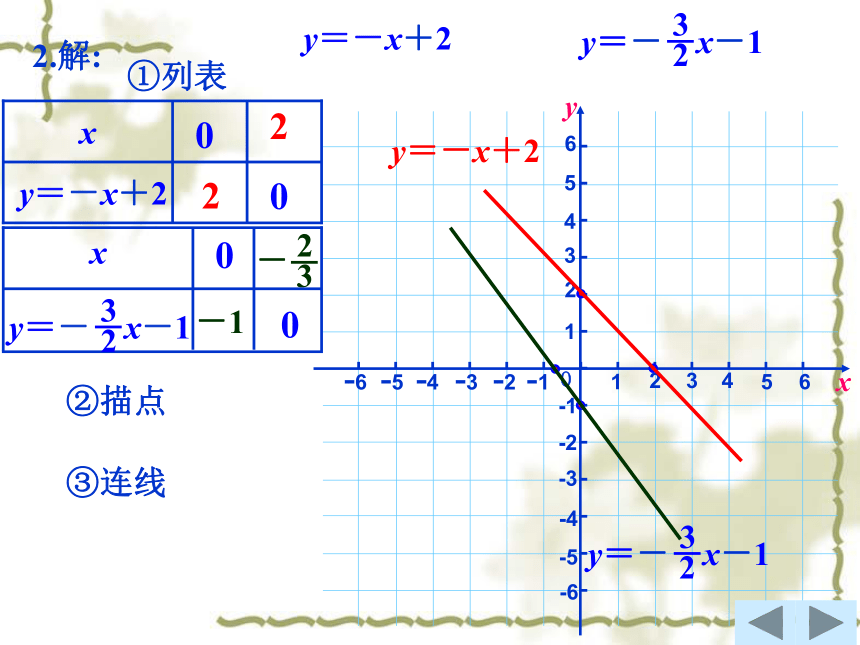
2.在同一直角坐标系中画出下列函数的图像:
y=-x+2
y=- x-1
3
2
和
-2
1
2
-3
-4
3
4
-1
5
y
6
-5
-6
1
2
3
4
5
O
-1
-2
-3
-4
x
6
-5
-6
y=3x-2
y= x +1
2
3
1.解:
①列表
②描点
③连线
-2
3
2
-
0
0
y=3x-2
x
1
2
3
2
3
y= x +1
x
0
0
y=3x-2
2
3
y= x +1
-2
1
2
-3
-4
3
4
-1
5
y
6
-5
-6
1
2
3
4
5
O
-1
-2
-3
-4
x
6
-5
-6
2.解:
①列表
②描点
③连线
2
2
3
-
0
0
y=-x+2
x
-1
x
0
0
y=- x-1
3
2
2
y=-x+2
y=- x-1
3
2
y=-x+2
y=- x-1
3
2
-2
1
2
-3
-4
3
4
-1
5
y
-5
1
2
3
4
5
O
-1
-2
-3
-4
x
-5
y= x+1
2
3
y=3x-2
y=-x+2
-2
1
2
-3
-4
3
4
-1
5
y
-5
1
2
3
4
5
O
-1
-2
-3
-4
x
-5
y=- x-1
3
2
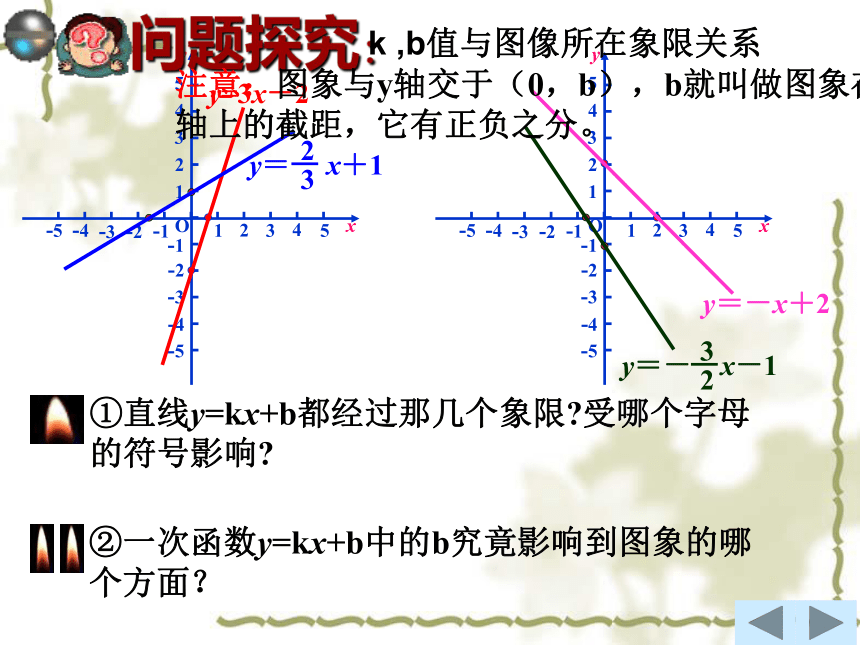
问题探究:
①直线y=kx+b都经过那几个象限 受哪个字母的符号影响
②一次函数y=kx+b中的b究竟影响到图象的哪个方面?
k ,b值与图像所在象限关系
注意:图象与y轴交于(0,b),b就叫做图象在y
轴上的截距,它有正负之分。
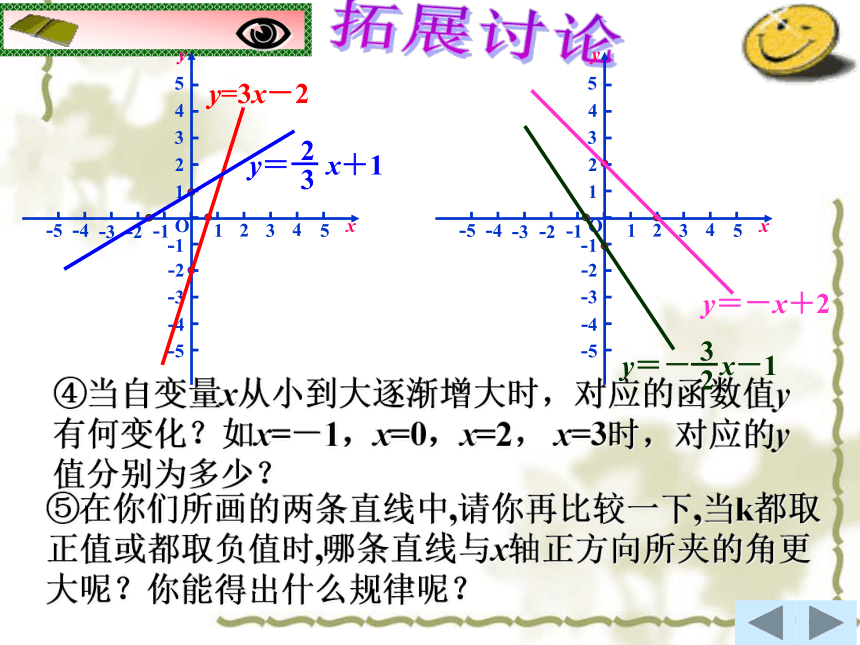
④当自变量x从小到大逐渐增大时,对应的函数值y有何变化?如x=-1,x=0,x=2, x=3时,对应的y值分别为多少?
⑤在你们所画的两条直线中,请你再比较一下,当k都取正值或都取负值时,哪条直线与x轴正方向所夹的角更大呢?你能得出什么规律呢?
-2
1
2
-3
-4
3
4
-1
5
y
-5
1
2
3
4
5
O
-1
-2
-3
-4
x
-5
y= x+1
2
3
y=3x-2
y=-x+2
-2
1
2
-3
-4
3
4
-1
5
y
-5
1
2
3
4
5
O
-1
-2
-3
-4
x
-5
y=- x-1
3
2
-2
1
2
-3
-4
3
4
-1
5
y
6
-5
-6
1
2
3
4
5
O
-1
-2
-3
-4
x
6
-5
-6
y=3x-2
y= x +1
2
3
x增大
y增大
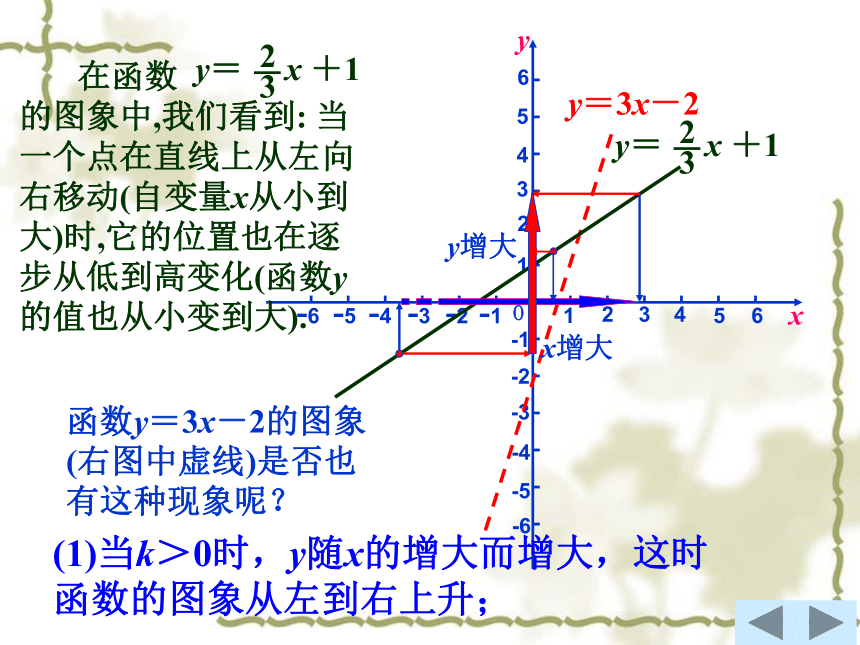
(1)当k>0时,y随x的增大而增大,这时函数的图象从左到右上升;
函数y=3x-2的图象(右图中虚线)是否也有这种现象呢?
在函数 的图象中,我们看到: 当一个点在直线上从左向右移动(自变量x从小到大)时,它的位置也在逐步从低到高变化(函数y的值也从小变到大).
y= x +1
2
3
-2
1
2
-3
-4
3
4
-1
5
y
6
-5
-6
1
2
3
4
5
O
-1
-2
-3
-4
x
6
-5
-6
y=-x+2
y=- x-1
3
2
x增大
y减小
(2) 当k<0时,y随x的
增大而_____,这时函数
的图象从左到右_____.
减小
下降
函数 的图象(右图中虚线)是否也有这种现象呢?
在函数y=-x+2 的图象中,我们看到: 当一个点在直线上从左向右移动(自变量x从小到大)时,它的位置也在逐步从高到低变化(函数y的值也从大变到小).
y=- x-1
3
2
一次函数y=kx+b有下列性质:
(1) 当k>0时,y随x的增大而增大,这时函数的图象随着自变量x的增大而从左到右上升;
(2) 当k<0时,y随x的增大而_____,这时函数的图象随着自变量x的增大而从左到右_____.
概括
减小
下降
例1 已知一次函数y=(m+1)x-3
(1)当m取何值时,y随x的增大而增大?
(2)当 m取何值时,y随x的增大而减小?
解:
(1)当m+1>0即m>-1时,y随x的增大而增大;
(2)当m+1<0即m<-1时,y随x的增大而减小.
例2 已知点(2,m)、(-3,n)都在直线 上,试比较 m和n的大小.你能想出几种判断的方法
所以函数y随x增大而增大 .
解: 方法一 把两点的坐标代入函数关系式
当 x=2 时, m=
当 x=-3 时, n=
所以 m > n .
方法二 因为 k=
> 0,
从而直接得到 m > n .
y= x +1
1
6
1
2
1
6
4
3
*
图 象
*k越小直线相对于x轴越陡峭.
*k越大直线相对于x轴越陡峭.
图象与y轴相交于负半轴,图象只经过二、三、四象限,不经过第一象限.
图象与y轴相交于正半轴,图象只经过一、二、四象限,不经过第三象限.
图象与y轴相交于负半轴,图象只经过一、三、四象限,不经过第二象限.
图象与y轴相交于正半轴,图象只经过一、二、三象限,不经过第四象限.
函数的图象随着x的增大从左到右下降.
函数的图象随着x的增大从左到右上升 .
y随x的增大而减小
y随x的增大而增大
一
次
函
数
的
性
质
b<0
b>0
b<0
b>0
y=kx+b (k≠0)
一次函数关系式
x
O
y
x
O
y
x
O
y
x
O
y
k>0
k<0
根据图象确定k,b的取值
K 0
b 0
K 0
b 0
K 0
b 0
K 0
b 0
K 0
b 0
K 0
b 0
K
b
>
=
<
=
<
>
<
<
>
<
>
>
*
抢答题
1在平面直角坐标系中,函数y=-2x+3的图象经过( )
A.一、二、三象限 B.二、三、四象限
C.一、三、四象限 D.一、二、四象限
2已知一次函数y=x-2的大致图像为 ( )
A B C D
D
C
1 一次函数y=x-2的图象不经过的象限为( )
(A) 一 (B) 二 (C) 三 (D) 四
2 不经过第二象限的直线是 ( )
(A) y=-2x (B) y=2x-1 (C) y=2x+1 (D) y=-2x+1
3 若直线 y=kx+b经过一二四象限,那么直线 y=-bx+k经过 象限
4 直线 y=kx-k的图象的大致位置是 ( )
A
B
C
D
B
B
二三四
C
*
试一试
下列一次函数中,y的值随x的增大而减小
的有________.
(1)、(3)
(1) y=-2x-1
(2) y=3x+2
(3) y=4-x
(4) y=5x-1
1.一次函数y=kx+b中,kb>0,且y随x的增大而
减小,画出的大致图象为( ).
C
D
C
B
A
拓展与应用
x
y
x
y
x
y
x
y
同学们:
今天你有哪些收获呢?
①函数图象与y轴交点是(0,b),
与x轴交点是(- ,0).
②当k>0,b>0时,函数图象过一、二、三象限,
y随x的增大而增大;
③当k>0,b<0时,函数图象过一、三、四象限,
y随x的增大而增大;
④当k>0,b=0时,函数图象过一、三象限,
y随x的增大而增大;
⑤当k<0,b>0时,函数图象过一、二、四象限,
y随x的增大而减小;
⑥当k<0,b<0时,函数图象过二、三、四象限,
y随x的增大而减小;
⑦当k<0,b=0时,函数图象过二、四象限,
y随x的增大而减小.
经过本节课的学习,你有哪些收获
b
k
作业:
课本47页习题4、5,6题
不经历风雨怎能见彩虹,没有谁能随随便便成功!加油!!
谢谢同学们,再见
教学目标:
[1]了解正比例函数及一次函数图象的有关性质;体会一次函数的图象的位置关系。
[2]会用简单方法画一次函数的图象;
[3]培养学生数形结合的意识和能力。
*
(1)列表
(2)描点
(3)连线
2、画函数图象的一般步骤:
1.什么是一次函数?什么是正比例函数?
如果y=kx+b(k,b是常数,k≠0),那么y叫做x的一次函数。特别的,当b=0时,y=kx+b就成为y=kx,这时,y叫做x的正比例函数。
*
这节课我们要借助函数图象研究一次函数的性质.
我们先来看下面的问题:
1.在同一直角坐标系中画出下列函数的图像:
y=3x-2
2
3
y= x +1
和
2.在同一直角坐标系中画出下列函数的图像:
y=-x+2
y=- x-1
3
2
和
-2
1
2
-3
-4
3
4
-1
5
y
6
-5
-6
1
2
3
4
5
O
-1
-2
-3
-4
x
6
-5
-6
y=3x-2
y= x +1
2
3
1.解:
①列表
②描点
③连线
-2
3
2
-
0
0
y=3x-2
x
1
2
3
2
3
y= x +1
x
0
0
y=3x-2
2
3
y= x +1
-2
1
2
-3
-4
3
4
-1
5
y
6
-5
-6
1
2
3
4
5
O
-1
-2
-3
-4
x
6
-5
-6
2.解:
①列表
②描点
③连线
2
2
3
-
0
0
y=-x+2
x
-1
x
0
0
y=- x-1
3
2
2
y=-x+2
y=- x-1
3
2
y=-x+2
y=- x-1
3
2
-2
1
2
-3
-4
3
4
-1
5
y
-5
1
2
3
4
5
O
-1
-2
-3
-4
x
-5
y= x+1
2
3
y=3x-2
y=-x+2
-2
1
2
-3
-4
3
4
-1
5
y
-5
1
2
3
4
5
O
-1
-2
-3
-4
x
-5
y=- x-1
3
2
问题探究:
①直线y=kx+b都经过那几个象限 受哪个字母的符号影响
②一次函数y=kx+b中的b究竟影响到图象的哪个方面?
k ,b值与图像所在象限关系
注意:图象与y轴交于(0,b),b就叫做图象在y
轴上的截距,它有正负之分。
④当自变量x从小到大逐渐增大时,对应的函数值y有何变化?如x=-1,x=0,x=2, x=3时,对应的y值分别为多少?
⑤在你们所画的两条直线中,请你再比较一下,当k都取正值或都取负值时,哪条直线与x轴正方向所夹的角更大呢?你能得出什么规律呢?
-2
1
2
-3
-4
3
4
-1
5
y
-5
1
2
3
4
5
O
-1
-2
-3
-4
x
-5
y= x+1
2
3
y=3x-2
y=-x+2
-2
1
2
-3
-4
3
4
-1
5
y
-5
1
2
3
4
5
O
-1
-2
-3
-4
x
-5
y=- x-1
3
2
-2
1
2
-3
-4
3
4
-1
5
y
6
-5
-6
1
2
3
4
5
O
-1
-2
-3
-4
x
6
-5
-6
y=3x-2
y= x +1
2
3
x增大
y增大
(1)当k>0时,y随x的增大而增大,这时函数的图象从左到右上升;
函数y=3x-2的图象(右图中虚线)是否也有这种现象呢?
在函数 的图象中,我们看到: 当一个点在直线上从左向右移动(自变量x从小到大)时,它的位置也在逐步从低到高变化(函数y的值也从小变到大).
y= x +1
2
3
-2
1
2
-3
-4
3
4
-1
5
y
6
-5
-6
1
2
3
4
5
O
-1
-2
-3
-4
x
6
-5
-6
y=-x+2
y=- x-1
3
2
x增大
y减小
(2) 当k<0时,y随x的
增大而_____,这时函数
的图象从左到右_____.
减小
下降
函数 的图象(右图中虚线)是否也有这种现象呢?
在函数y=-x+2 的图象中,我们看到: 当一个点在直线上从左向右移动(自变量x从小到大)时,它的位置也在逐步从高到低变化(函数y的值也从大变到小).
y=- x-1
3
2
一次函数y=kx+b有下列性质:
(1) 当k>0时,y随x的增大而增大,这时函数的图象随着自变量x的增大而从左到右上升;
(2) 当k<0时,y随x的增大而_____,这时函数的图象随着自变量x的增大而从左到右_____.
概括
减小
下降
例1 已知一次函数y=(m+1)x-3
(1)当m取何值时,y随x的增大而增大?
(2)当 m取何值时,y随x的增大而减小?
解:
(1)当m+1>0即m>-1时,y随x的增大而增大;
(2)当m+1<0即m<-1时,y随x的增大而减小.
例2 已知点(2,m)、(-3,n)都在直线 上,试比较 m和n的大小.你能想出几种判断的方法
所以函数y随x增大而增大 .
解: 方法一 把两点的坐标代入函数关系式
当 x=2 时, m=
当 x=-3 时, n=
所以 m > n .
方法二 因为 k=
> 0,
从而直接得到 m > n .
y= x +1
1
6
1
2
1
6
4
3
*
图 象
*k越小直线相对于x轴越陡峭.
*k越大直线相对于x轴越陡峭.
图象与y轴相交于负半轴,图象只经过二、三、四象限,不经过第一象限.
图象与y轴相交于正半轴,图象只经过一、二、四象限,不经过第三象限.
图象与y轴相交于负半轴,图象只经过一、三、四象限,不经过第二象限.
图象与y轴相交于正半轴,图象只经过一、二、三象限,不经过第四象限.
函数的图象随着x的增大从左到右下降.
函数的图象随着x的增大从左到右上升 .
y随x的增大而减小
y随x的增大而增大
一
次
函
数
的
性
质
b<0
b>0
b<0
b>0
y=kx+b (k≠0)
一次函数关系式
x
O
y
x
O
y
x
O
y
x
O
y
k>0
k<0
根据图象确定k,b的取值
K 0
b 0
K 0
b 0
K 0
b 0
K 0
b 0
K 0
b 0
K 0
b 0
K
b
>
=
<
=
<
>
<
<
>
<
>
>
*
抢答题
1在平面直角坐标系中,函数y=-2x+3的图象经过( )
A.一、二、三象限 B.二、三、四象限
C.一、三、四象限 D.一、二、四象限
2已知一次函数y=x-2的大致图像为 ( )
A B C D
D
C
1 一次函数y=x-2的图象不经过的象限为( )
(A) 一 (B) 二 (C) 三 (D) 四
2 不经过第二象限的直线是 ( )
(A) y=-2x (B) y=2x-1 (C) y=2x+1 (D) y=-2x+1
3 若直线 y=kx+b经过一二四象限,那么直线 y=-bx+k经过 象限
4 直线 y=kx-k的图象的大致位置是 ( )
A
B
C
D
B
B
二三四
C
*
试一试
下列一次函数中,y的值随x的增大而减小
的有________.
(1)、(3)
(1) y=-2x-1
(2) y=3x+2
(3) y=4-x
(4) y=5x-1
1.一次函数y=kx+b中,kb>0,且y随x的增大而
减小,画出的大致图象为( ).
C
D
C
B
A
拓展与应用
x
y
x
y
x
y
x
y
同学们:
今天你有哪些收获呢?
①函数图象与y轴交点是(0,b),
与x轴交点是(- ,0).
②当k>0,b>0时,函数图象过一、二、三象限,
y随x的增大而增大;
③当k>0,b<0时,函数图象过一、三、四象限,
y随x的增大而增大;
④当k>0,b=0时,函数图象过一、三象限,
y随x的增大而增大;
⑤当k<0,b>0时,函数图象过一、二、四象限,
y随x的增大而减小;
⑥当k<0,b<0时,函数图象过二、三、四象限,
y随x的增大而减小;
⑦当k<0,b=0时,函数图象过二、四象限,
y随x的增大而减小.
经过本节课的学习,你有哪些收获
b
k
作业:
课本47页习题4、5,6题
不经历风雨怎能见彩虹,没有谁能随随便便成功!加油!!
谢谢同学们,再见
