华东师大版数学八年级上册 13.2.2 全等三角形的判定条件课件(共19张PPT)
文档属性
| 名称 | 华东师大版数学八年级上册 13.2.2 全等三角形的判定条件课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 790.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-25 00:00:00 | ||
图片预览

文档简介
(共19张PPT)
全等三角形的判定条件
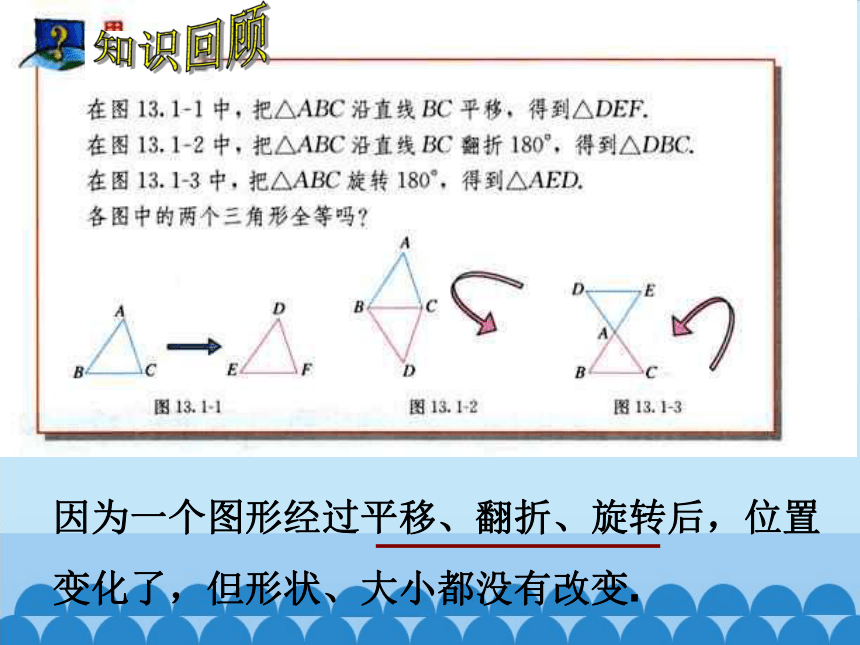
因为一个图形经过平移、翻折、旋转后,位置
变化了,但形状、大小都没有改变.
知识回顾
A
B
C
D
E
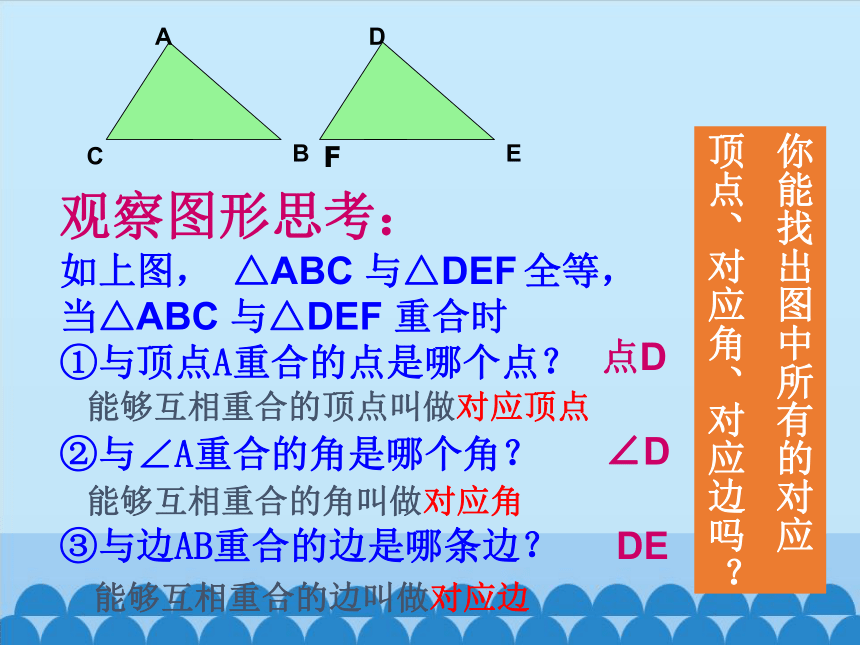
观察图形思考:
如上图, △ABC 与△DEF 全等,
当△ABC 与△DEF 重合时
①与顶点A重合的点是哪个点?
②与∠A重合的角是哪个角?
③与边AB重合的边是哪条边?
点D
能够互相重合的顶点叫做对应顶点
∠D
能够互相重合的角叫做对应角
DE
能够互相重合的边叫做对应边
F
你能找出图中所有的对应
顶点、对应角、对应边吗?
A
B
C
D
E
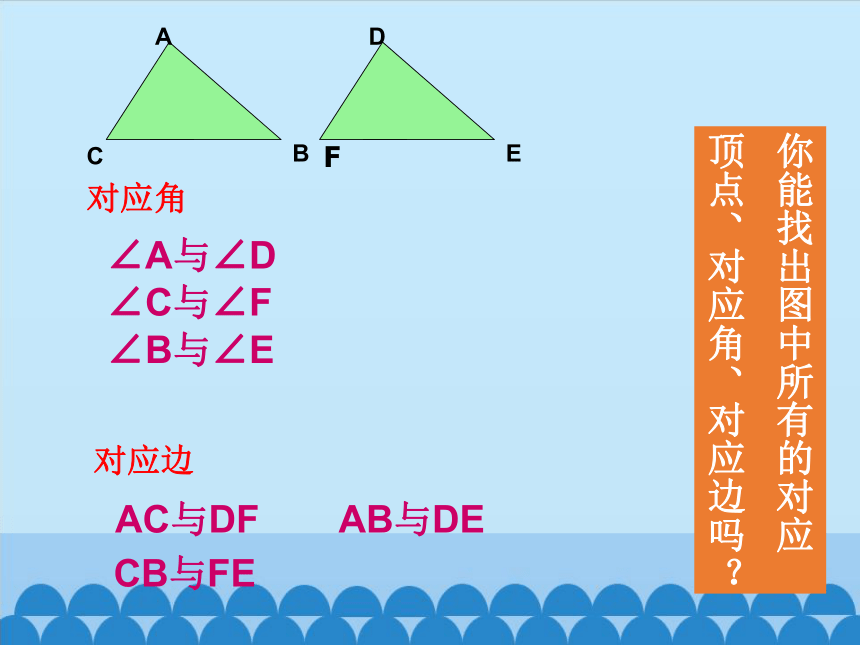
∠A与∠D
对应角
AC与DF
对应边
F
你能找出图中所有的对应
顶点、对应角、对应边吗?
∠C与∠F
∠B与∠E
AB与DE
CB与FE
A
B
C
D
E
F
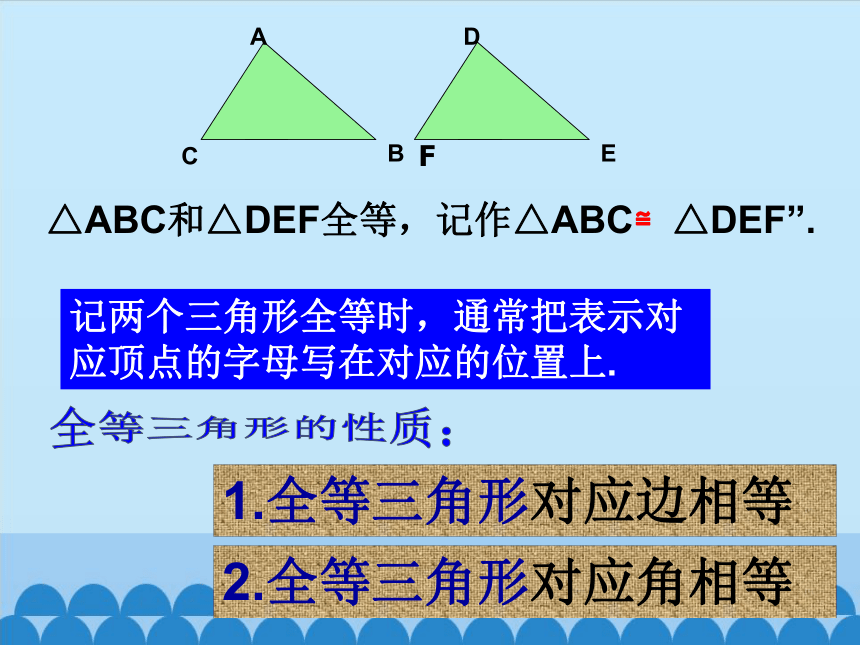
△ABC和△DEF全等,记作△ABC≌△DEF”.
记两个三角形全等时,通常把表示对应顶点的字母写在对应的位置上.
全等三角形的性质:
1.全等三角形对应边相等
2.全等三角形对应角相等
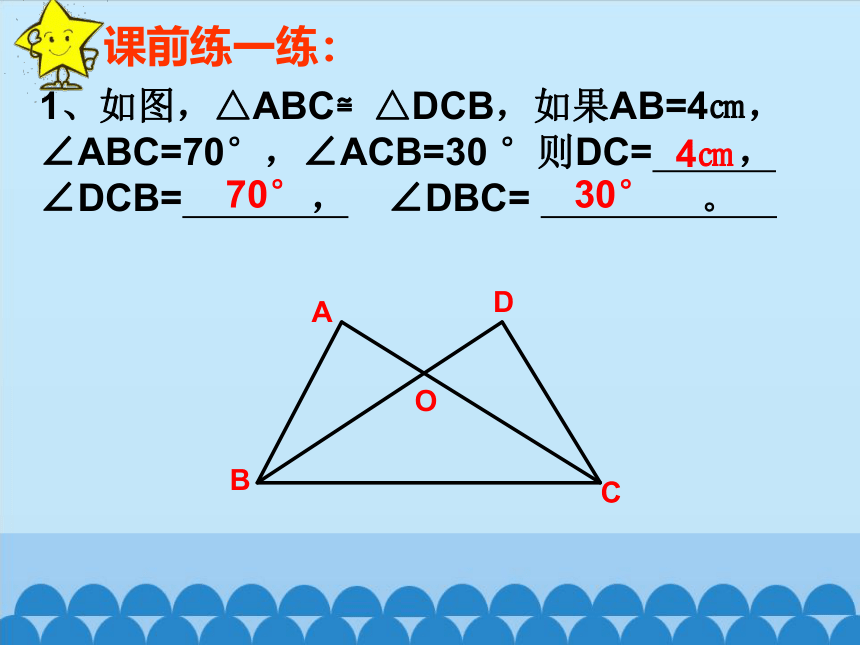
1、如图,△ABC≌△DCB,如果AB=4㎝,
∠ABC=70°,∠ACB=30 °则DC= ,
∠DCB= , ∠DBC= 。
4㎝
70°
30°
课前练一练:
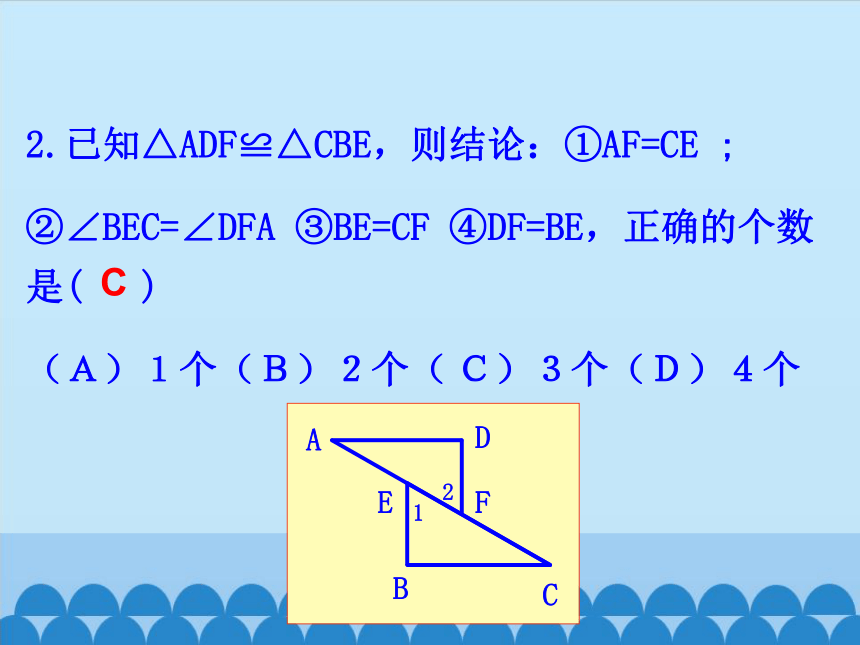
2.已知△ADF≌△CBE,则结论:①AF=CE ;
②∠BEC=∠DFA ③BE=CF ④DF=BE,正确的个数是( )
(A)1个(B)2个( C)3个(D)4个
C
某检查人员到工厂检查三角形模型尺寸是否合格。其中标准模型尺寸如图,如果你是检查人员,你至少需要量出几个数据,才能判断出两个三角形模型全等呢?
6
4
5
β
γ
α
帮帮我
探索全等三角形的判定条件
想一想:
(1)面积相等的两个三角形一定全等吗?
(2)周长相等的两个三角形一定全等吗?
想一想:
再想一想:
全等三角形的性质:
1.全等三角形对应边相等
2.全等三角形对应角相等
我们知道:若两个三角形的三条边、三个角分别
对应相等,则这两个三角形全等?
一定要六个条件那么多吗?
我们确实可以减少一些条件:
我们知道:由于三角形的内角和等于1800,如果
两个角对应相等,那么另一个角必然
也相等。这样我们只要三条边,两个
角相等五个条件就够了?
问题:
能否再减少一些?
对六个条件而言至少要有几个元素分别对应相等,两个三角形才全等呢?
1、当两个三角形只有一组对应边相等(3cm)
或一组对应角相等(600)时,它们全等吗?
让我们从最简单的开始吧?
一个条件
2、两个三角形中,
(1)有两组对应边分别相等(假如为3cm和5cm),它们全等吗?
(2)有两组对应角分别相等(分别为500和700),
它们全等吗?
两个条件
(两组边相等)
(3)有一组对应边、一组对应角角分别相等
(分别为600和3cm),它们全等吗?
两个条件
1、这条长3cm的边是600角的邻边
2、这条长3cm的边是600角的对边
一个条件
两个条件
条件都还不够
归纳
3、再增加一个条件有哪几种情况?
(1)、两边一角;
(2)、两角一边;
(3)、边边边;
(4)、角角角
三个条件
条件够了吗?
小结
1、回顾全等三角形的性质
2、经过探索发现要判定两个三角形全等
不需要满足三条对应边,三个对应角
同时对应相等
3、经过探索发现要判定两个三角形全等
仅仅一个或两个条件对应相等是不够的
谢谢!
全等三角形的判定条件
因为一个图形经过平移、翻折、旋转后,位置
变化了,但形状、大小都没有改变.
知识回顾
A
B
C
D
E
观察图形思考:
如上图, △ABC 与△DEF 全等,
当△ABC 与△DEF 重合时
①与顶点A重合的点是哪个点?
②与∠A重合的角是哪个角?
③与边AB重合的边是哪条边?
点D
能够互相重合的顶点叫做对应顶点
∠D
能够互相重合的角叫做对应角
DE
能够互相重合的边叫做对应边
F
你能找出图中所有的对应
顶点、对应角、对应边吗?
A
B
C
D
E
∠A与∠D
对应角
AC与DF
对应边
F
你能找出图中所有的对应
顶点、对应角、对应边吗?
∠C与∠F
∠B与∠E
AB与DE
CB与FE
A
B
C
D
E
F
△ABC和△DEF全等,记作△ABC≌△DEF”.
记两个三角形全等时,通常把表示对应顶点的字母写在对应的位置上.
全等三角形的性质:
1.全等三角形对应边相等
2.全等三角形对应角相等
1、如图,△ABC≌△DCB,如果AB=4㎝,
∠ABC=70°,∠ACB=30 °则DC= ,
∠DCB= , ∠DBC= 。
4㎝
70°
30°
课前练一练:
2.已知△ADF≌△CBE,则结论:①AF=CE ;
②∠BEC=∠DFA ③BE=CF ④DF=BE,正确的个数是( )
(A)1个(B)2个( C)3个(D)4个
C
某检查人员到工厂检查三角形模型尺寸是否合格。其中标准模型尺寸如图,如果你是检查人员,你至少需要量出几个数据,才能判断出两个三角形模型全等呢?
6
4
5
β
γ
α
帮帮我
探索全等三角形的判定条件
想一想:
(1)面积相等的两个三角形一定全等吗?
(2)周长相等的两个三角形一定全等吗?
想一想:
再想一想:
全等三角形的性质:
1.全等三角形对应边相等
2.全等三角形对应角相等
我们知道:若两个三角形的三条边、三个角分别
对应相等,则这两个三角形全等?
一定要六个条件那么多吗?
我们确实可以减少一些条件:
我们知道:由于三角形的内角和等于1800,如果
两个角对应相等,那么另一个角必然
也相等。这样我们只要三条边,两个
角相等五个条件就够了?
问题:
能否再减少一些?
对六个条件而言至少要有几个元素分别对应相等,两个三角形才全等呢?
1、当两个三角形只有一组对应边相等(3cm)
或一组对应角相等(600)时,它们全等吗?
让我们从最简单的开始吧?
一个条件
2、两个三角形中,
(1)有两组对应边分别相等(假如为3cm和5cm),它们全等吗?
(2)有两组对应角分别相等(分别为500和700),
它们全等吗?
两个条件
(两组边相等)
(3)有一组对应边、一组对应角角分别相等
(分别为600和3cm),它们全等吗?
两个条件
1、这条长3cm的边是600角的邻边
2、这条长3cm的边是600角的对边
一个条件
两个条件
条件都还不够
归纳
3、再增加一个条件有哪几种情况?
(1)、两边一角;
(2)、两角一边;
(3)、边边边;
(4)、角角角
三个条件
条件够了吗?
小结
1、回顾全等三角形的性质
2、经过探索发现要判定两个三角形全等
不需要满足三条对应边,三个对应角
同时对应相等
3、经过探索发现要判定两个三角形全等
仅仅一个或两个条件对应相等是不够的
谢谢!
