华东师大版数学八年级上册 13.5.3角平分线课件(共17张PPT)
文档属性
| 名称 | 华东师大版数学八年级上册 13.5.3角平分线课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 464.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-26 10:37:23 | ||
图片预览





文档简介
(共17张PPT)
角平分线
请你帮帮它
如图,两条小河交汇形成的三角区,土壤肥沃,气候宜人,小猪看中了这块宝地,想在这里建一个小房子,并使房子到两条小河的距离相等,但它不知该如何选址,你能帮帮它吗?
房子该建在哪儿呢?
情境导航
学习目标:
1.经历角平分线的性质的证明过程,掌握角平分线的性质定理及其逆定理.
2.能运用角平分线的性质定理及其逆定理解决有关问题.
3.通过观察、类比、归纳等方法尝试从不同角度分析问题,提高解决问题的能力。
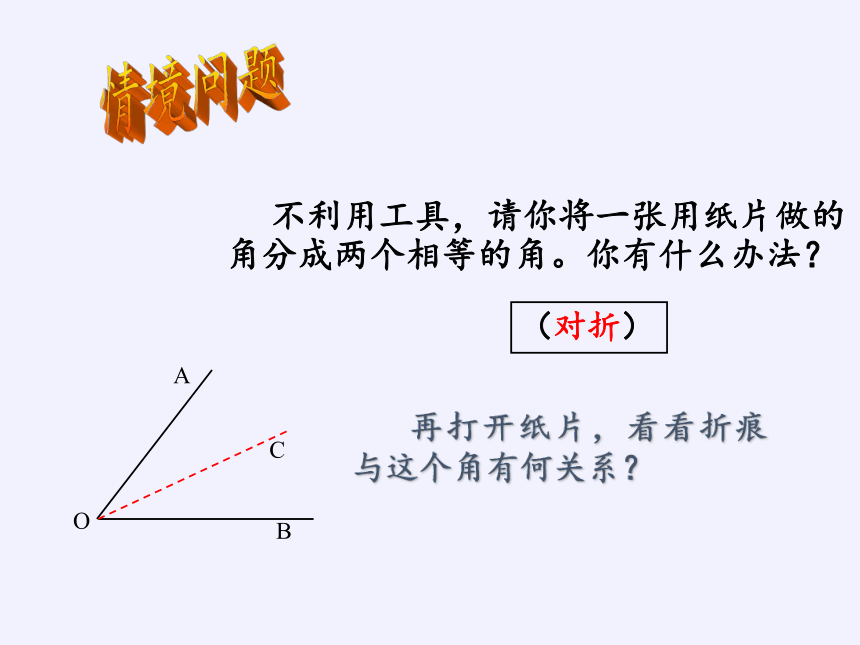
不利用工具,请你将一张用纸片做的角分成两个相等的角。你有什么办法?
A
O
B
C
再打开纸片,看看折痕与这个角有何关系?
(对折)
情境问题
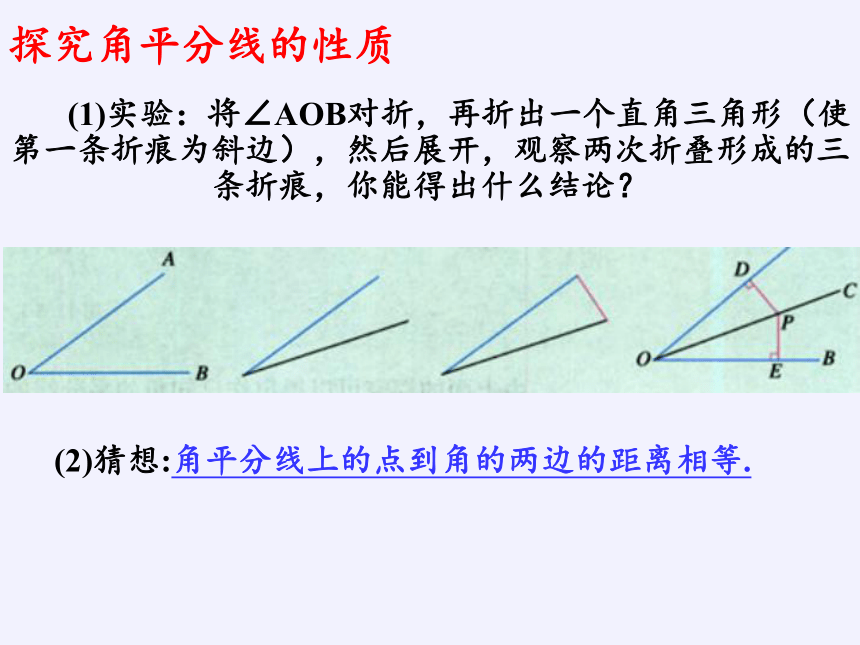
探究角平分线的性质
(1)实验:将∠AOB对折,再折出一个直角三角形(使第一条折痕为斜边),然后展开,观察两次折叠形成的三条折痕,你能得出什么结论?
(2)猜想:角平分线上的点到角的两边的距离相等.
证明:∵OC平分∠ AOB (已知)
∴ ∠1= ∠2(角平分线的定义)
∵PD ⊥ OA,PE ⊥ OB
∴ ∠PDO= ∠PEO=900
在△PDO和△PEO中,
∵∠PDO= ∠PEO(已证)
∠1= ∠2 (已证)
OP=OP (公共边)
∴ △PDO ≌ △PEO(A.A.S.)
∴PD=PE(全等三角形的对应边相等)
P
A
O
B
C
E
D
1
2
已知:如图,OC平分∠AOB,点P在OC上,PD⊥OA于点D,PE⊥OB于点E
求证: PD=PE
(3)验证猜想
几何语言表示为:
∵ ∠1= ∠2, PD ⊥ OA, PE ⊥ OB(已知)∴PD=PE(角平分线上的点到角两边的距离相等)
P
A
O
B
C
E
D
1
2
(4)得到角平分线的性质:
角平分线上的点到角两边的距离相等。
1、请你写出角平分线性质定理的逆命题:
2、这个命题是否正确?你能用逻辑推理的方法加以验证吗?试一试。
交流总结
角的内部 到角两边距离相等的点,在这个角的平分线上
证明: 过点O、Q作射线OQ.
∵ QD⊥OA,QE⊥OB(已知),
∴ ∠QDO=∠QEO=90° (垂直的定义)
在Rt△QDO和Rt△QEO中
∵ QO=QO(公共边)
QD=QE
∴ Rt△QDO≌Rt△QEO(HL)
∴ ∠ QOD=∠QOE
∴点Q在∠AOB的平分线上
已知:如图,QD⊥OA,QE⊥OB,
点D、E为垂足,QD=QE.
求证:点Q在∠AOB的平分线上.
角的内部到角两边距离相等的点在角的平分线上。
∵ QD⊥OA,QE⊥OB,QD=QE.
∴点Q在∠AOB的平分线上.
用几何语言表示为:
总结归纳:
角平分线性质定理的逆定理
角平分线的判定定理
如图, △ABC的角平分线BM,CN相交于点P,
求证:点P也在∠BAC的平分线上.
∵BM是△ABC的角平分线,点P在BM上, PD⊥AB, PE⊥BC
A
B
C
P
M
N
D
E
F
∴PD=PE
(角平分线上的点到这个角两边的距离相等).
同理,PE=PF.
∴PD=PF.
证明:过点P作PD⊥AB于D,PE⊥BC于E,PF⊥AC于F
∴点P在∠BAC的平分线上.
试一试
通过本题的证明,你能得到一个关于三角形角平分线的什么结论?
三角形的三条角平分线交于一点,并且交点到三角形三边的距离相等。
想一想
判断题( )
∵ 如图,AD平分∠BAC(已知)
∴BD = DC
(角的平分线上的点到角的两边的距离相等。)
×
1、如图,点P是菱形ABCD的对角线上一点,PE⊥AB于点E,PF⊥AD于点F,已知PF=5,则PE=
2、如图,点P到∠AOB两边的距离相等,若∠POB=30°,则∠AOB=
学以致用
O
P
A
B
5
60°
B
D
A
C
F
E
P
通过本节课的学习,你有哪些收获?
与你的同伴交流一下。
课堂小结
布置作业:
1、必做题:课本P98练习1、2;
2、选做题:如图,在△ABC中,∠A=90°,AB=AC,BD是∠ABC的平分线,DE⊥BC于E,且BC=8 cm,求△DEC的周长。
B
A
D
E
C
谢 谢
角平分线
请你帮帮它
如图,两条小河交汇形成的三角区,土壤肥沃,气候宜人,小猪看中了这块宝地,想在这里建一个小房子,并使房子到两条小河的距离相等,但它不知该如何选址,你能帮帮它吗?
房子该建在哪儿呢?
情境导航
学习目标:
1.经历角平分线的性质的证明过程,掌握角平分线的性质定理及其逆定理.
2.能运用角平分线的性质定理及其逆定理解决有关问题.
3.通过观察、类比、归纳等方法尝试从不同角度分析问题,提高解决问题的能力。
不利用工具,请你将一张用纸片做的角分成两个相等的角。你有什么办法?
A
O
B
C
再打开纸片,看看折痕与这个角有何关系?
(对折)
情境问题
探究角平分线的性质
(1)实验:将∠AOB对折,再折出一个直角三角形(使第一条折痕为斜边),然后展开,观察两次折叠形成的三条折痕,你能得出什么结论?
(2)猜想:角平分线上的点到角的两边的距离相等.
证明:∵OC平分∠ AOB (已知)
∴ ∠1= ∠2(角平分线的定义)
∵PD ⊥ OA,PE ⊥ OB
∴ ∠PDO= ∠PEO=900
在△PDO和△PEO中,
∵∠PDO= ∠PEO(已证)
∠1= ∠2 (已证)
OP=OP (公共边)
∴ △PDO ≌ △PEO(A.A.S.)
∴PD=PE(全等三角形的对应边相等)
P
A
O
B
C
E
D
1
2
已知:如图,OC平分∠AOB,点P在OC上,PD⊥OA于点D,PE⊥OB于点E
求证: PD=PE
(3)验证猜想
几何语言表示为:
∵ ∠1= ∠2, PD ⊥ OA, PE ⊥ OB(已知)∴PD=PE(角平分线上的点到角两边的距离相等)
P
A
O
B
C
E
D
1
2
(4)得到角平分线的性质:
角平分线上的点到角两边的距离相等。
1、请你写出角平分线性质定理的逆命题:
2、这个命题是否正确?你能用逻辑推理的方法加以验证吗?试一试。
交流总结
角的内部 到角两边距离相等的点,在这个角的平分线上
证明: 过点O、Q作射线OQ.
∵ QD⊥OA,QE⊥OB(已知),
∴ ∠QDO=∠QEO=90° (垂直的定义)
在Rt△QDO和Rt△QEO中
∵ QO=QO(公共边)
QD=QE
∴ Rt△QDO≌Rt△QEO(HL)
∴ ∠ QOD=∠QOE
∴点Q在∠AOB的平分线上
已知:如图,QD⊥OA,QE⊥OB,
点D、E为垂足,QD=QE.
求证:点Q在∠AOB的平分线上.
角的内部到角两边距离相等的点在角的平分线上。
∵ QD⊥OA,QE⊥OB,QD=QE.
∴点Q在∠AOB的平分线上.
用几何语言表示为:
总结归纳:
角平分线性质定理的逆定理
角平分线的判定定理
如图, △ABC的角平分线BM,CN相交于点P,
求证:点P也在∠BAC的平分线上.
∵BM是△ABC的角平分线,点P在BM上, PD⊥AB, PE⊥BC
A
B
C
P
M
N
D
E
F
∴PD=PE
(角平分线上的点到这个角两边的距离相等).
同理,PE=PF.
∴PD=PF.
证明:过点P作PD⊥AB于D,PE⊥BC于E,PF⊥AC于F
∴点P在∠BAC的平分线上.
试一试
通过本题的证明,你能得到一个关于三角形角平分线的什么结论?
三角形的三条角平分线交于一点,并且交点到三角形三边的距离相等。
想一想
判断题( )
∵ 如图,AD平分∠BAC(已知)
∴BD = DC
(角的平分线上的点到角的两边的距离相等。)
×
1、如图,点P是菱形ABCD的对角线上一点,PE⊥AB于点E,PF⊥AD于点F,已知PF=5,则PE=
2、如图,点P到∠AOB两边的距离相等,若∠POB=30°,则∠AOB=
学以致用
O
P
A
B
5
60°
B
D
A
C
F
E
P
通过本节课的学习,你有哪些收获?
与你的同伴交流一下。
课堂小结
布置作业:
1、必做题:课本P98练习1、2;
2、选做题:如图,在△ABC中,∠A=90°,AB=AC,BD是∠ABC的平分线,DE⊥BC于E,且BC=8 cm,求△DEC的周长。
B
A
D
E
C
谢 谢
