小学数学北师大版六年级下1.4 圆柱的表面积(二)课件(共15张PPT)
文档属性
| 名称 | 小学数学北师大版六年级下1.4 圆柱的表面积(二)课件(共15张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-29 17:00:46 | ||
图片预览





文档简介
(共15张PPT)
一 圆柱与圆锥
第4课时 圆柱的表面积(二)
一、复习引入
圆柱的侧、表面积的计算公式。
圆柱的侧面积 = 底面周长 × 高
S侧 = Ch
圆柱的表面积 = 圆柱的侧面积 + 两个底面的面积
S表 = S侧 + 2S底
二、学习新课
如图,做一个无盖的圆柱形铁皮水桶,底面直径为4dm,高为5dm,至少需要用多大面积的铁皮?
4dm
5dm
铁皮的面积 = 侧面积 + 一个底面积
侧面积:
底面积:
需要铁皮的面积:
12.56×5=62.8(dm2)
3.14×(4÷2)2=12.56(dm2)
62.8+12.56=75.36(dm2)
答:至少需要75.36dm2的铁皮。
底面周长:
3.14×4=12.56(dm)
二、学习新课
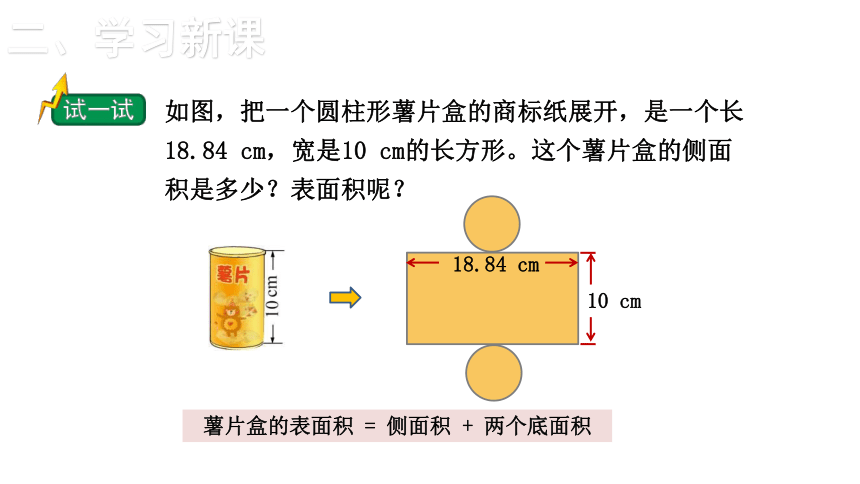
如图,把一个圆柱形薯片盒的商标纸展开,是一个长18.84 cm,宽是10 cm的长方形。这个薯片盒的侧面积是多少?表面积呢?
10 cm
18.84 cm
薯片盒的表面积 = 侧面积 + 两个底面积
二、学习新课
如图,把一个圆柱形薯片盒的商标纸展开,是一个长18.84cm,宽是10cm的长方形。这个薯片盒的侧面积是多少?表面积呢?
侧面积:
18.84×10=188.4(cm2)
底面半径:
18.84÷3.14÷2=3(cm)
底面积:
3.14×32×2=56.52(cm2)
表面积:
188.4+56.52=244.92(cm2)
答:这个薯片盒的侧面积是188.4cm2,表面积是244.92cm2。
二、学习新课
1. 压路机前轮直径是1.6 m,宽2 m,它转动一周,压路的面积是多少平方米?
圆柱的侧面积
3.14×1.6×2=10.048(m2)
答:压路的面积是10.048 m2。
二、学习新课
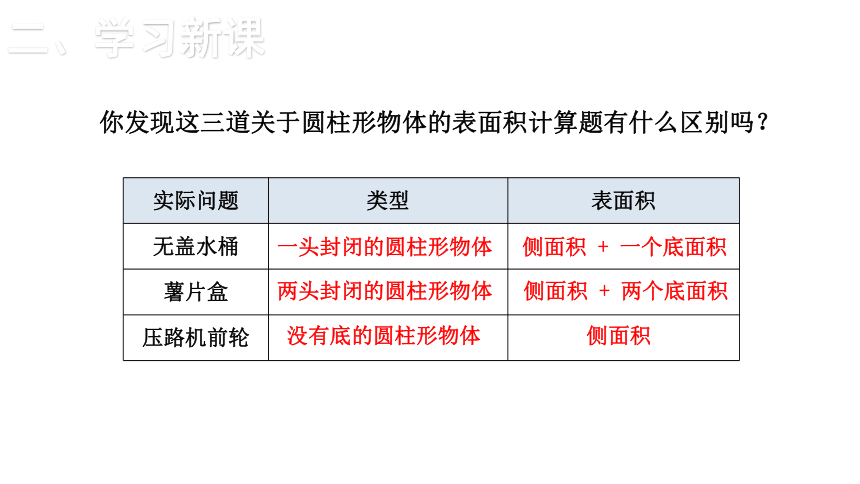
你发现这三道关于圆柱形物体的表面积计算题有什么区别吗?
实际问题 类型 表面积
无盖水桶
薯片盒
压路机前轮
一头封闭的圆柱形物体
侧面积 + 一个底面积
两头封闭的圆柱形物体
侧面积 + 两个底面积
没有底的圆柱形物体
侧面积
二、学习新课
解决问题实际问题时,不是所有的圆柱形物体都有两个底面,有的只有一个,有的没有底面,解题时要分清计算哪几个面的面积和。
三、巩固练习
3. 制作一个底面直径20cm,长50cm的圆柱形通风管,至少要用多少平方厘米的铁皮?
3.14×20×50=3140(cm2)
答:至少要用3140 cm2的铁皮。
圆柱的侧面积
三、巩固练习
5. 一个圆柱形水池,水池内壁和底部都镶上瓷砖,水池内部底面周长25.12m,池深1.2m,镶瓷砖的面积是多少平方米?
底面积:3.14×(25.12÷3.14÷2)2=50.24(m2)
侧面积:25.12×1.2=30.144(m2)
表面积:30.144+50.24=80.384(m2)
圆柱的侧面积 + 一个底面积
答:镶瓷砖的面积是80.384 m2。
三、巩固练习
7. 油桶的表面要刷上防锈油漆,每平方米需用防锈油漆0.2kg,刷一个油桶大约需要多少防锈油漆?(结果保留两位小数)
侧面积:3.14×0.6×1=1.884(m2)
底面积:3.14×(0.6÷2)2×2=0.5652(m2)
表面积:1.884+0.5652=2.4492(m2)
油漆:2.4492×0.2≈0.49(kg)
圆柱的侧面积 + 两个底面积
答:刷一个油桶大约需要0.49 kg防锈油漆。
三、巩固练习
8.如图,用下面的长方形硬纸卷成圆柱形小笔筒,再给这个笔筒配一个底, 想一想,至少还需要多少平方厘米的硬纸片
18.84 cm
12.56 cm
三、巩固练习
8.如图,用下面的长方形硬纸卷成圆柱形小笔筒,再给这个笔筒配一个底, 想一想,至少还需要多少平方厘米的硬纸片
18.84 cm
12.56 cm
①以12.56 cm为笔筒的高
还需要硬纸片:3.14×(18.84÷3.14÷2)2=28.26(cm2)
三、巩固练习
8.如图,用下面的长方形硬纸卷成圆柱形小笔筒,再给这个笔筒配一个底, 想一想,至少还需要多少平方厘米的硬纸片
18.84 cm
12.56 cm
②以18.84 cm为笔筒的高
还需要硬纸片:3.14×(12.56÷3.14÷2)2=12.56(cm2)
答:至少还需要12.56 cm2的硬纸片。
28.26>12.56
四、课堂小结
实际问题 类型 表面积
无盖水桶
薯片盒
压路机前轮
一头封闭的圆柱形物体
侧面积 + 一个底面积
两头封闭的圆柱形物体
侧面积 + 两个底面积
没有底的圆柱形物体
侧面积
一 圆柱与圆锥
第4课时 圆柱的表面积(二)
一、复习引入
圆柱的侧、表面积的计算公式。
圆柱的侧面积 = 底面周长 × 高
S侧 = Ch
圆柱的表面积 = 圆柱的侧面积 + 两个底面的面积
S表 = S侧 + 2S底
二、学习新课
如图,做一个无盖的圆柱形铁皮水桶,底面直径为4dm,高为5dm,至少需要用多大面积的铁皮?
4dm
5dm
铁皮的面积 = 侧面积 + 一个底面积
侧面积:
底面积:
需要铁皮的面积:
12.56×5=62.8(dm2)
3.14×(4÷2)2=12.56(dm2)
62.8+12.56=75.36(dm2)
答:至少需要75.36dm2的铁皮。
底面周长:
3.14×4=12.56(dm)
二、学习新课
如图,把一个圆柱形薯片盒的商标纸展开,是一个长18.84 cm,宽是10 cm的长方形。这个薯片盒的侧面积是多少?表面积呢?
10 cm
18.84 cm
薯片盒的表面积 = 侧面积 + 两个底面积
二、学习新课
如图,把一个圆柱形薯片盒的商标纸展开,是一个长18.84cm,宽是10cm的长方形。这个薯片盒的侧面积是多少?表面积呢?
侧面积:
18.84×10=188.4(cm2)
底面半径:
18.84÷3.14÷2=3(cm)
底面积:
3.14×32×2=56.52(cm2)
表面积:
188.4+56.52=244.92(cm2)
答:这个薯片盒的侧面积是188.4cm2,表面积是244.92cm2。
二、学习新课
1. 压路机前轮直径是1.6 m,宽2 m,它转动一周,压路的面积是多少平方米?
圆柱的侧面积
3.14×1.6×2=10.048(m2)
答:压路的面积是10.048 m2。
二、学习新课
你发现这三道关于圆柱形物体的表面积计算题有什么区别吗?
实际问题 类型 表面积
无盖水桶
薯片盒
压路机前轮
一头封闭的圆柱形物体
侧面积 + 一个底面积
两头封闭的圆柱形物体
侧面积 + 两个底面积
没有底的圆柱形物体
侧面积
二、学习新课
解决问题实际问题时,不是所有的圆柱形物体都有两个底面,有的只有一个,有的没有底面,解题时要分清计算哪几个面的面积和。
三、巩固练习
3. 制作一个底面直径20cm,长50cm的圆柱形通风管,至少要用多少平方厘米的铁皮?
3.14×20×50=3140(cm2)
答:至少要用3140 cm2的铁皮。
圆柱的侧面积
三、巩固练习
5. 一个圆柱形水池,水池内壁和底部都镶上瓷砖,水池内部底面周长25.12m,池深1.2m,镶瓷砖的面积是多少平方米?
底面积:3.14×(25.12÷3.14÷2)2=50.24(m2)
侧面积:25.12×1.2=30.144(m2)
表面积:30.144+50.24=80.384(m2)
圆柱的侧面积 + 一个底面积
答:镶瓷砖的面积是80.384 m2。
三、巩固练习
7. 油桶的表面要刷上防锈油漆,每平方米需用防锈油漆0.2kg,刷一个油桶大约需要多少防锈油漆?(结果保留两位小数)
侧面积:3.14×0.6×1=1.884(m2)
底面积:3.14×(0.6÷2)2×2=0.5652(m2)
表面积:1.884+0.5652=2.4492(m2)
油漆:2.4492×0.2≈0.49(kg)
圆柱的侧面积 + 两个底面积
答:刷一个油桶大约需要0.49 kg防锈油漆。
三、巩固练习
8.如图,用下面的长方形硬纸卷成圆柱形小笔筒,再给这个笔筒配一个底, 想一想,至少还需要多少平方厘米的硬纸片
18.84 cm
12.56 cm
三、巩固练习
8.如图,用下面的长方形硬纸卷成圆柱形小笔筒,再给这个笔筒配一个底, 想一想,至少还需要多少平方厘米的硬纸片
18.84 cm
12.56 cm
①以12.56 cm为笔筒的高
还需要硬纸片:3.14×(18.84÷3.14÷2)2=28.26(cm2)
三、巩固练习
8.如图,用下面的长方形硬纸卷成圆柱形小笔筒,再给这个笔筒配一个底, 想一想,至少还需要多少平方厘米的硬纸片
18.84 cm
12.56 cm
②以18.84 cm为笔筒的高
还需要硬纸片:3.14×(12.56÷3.14÷2)2=12.56(cm2)
答:至少还需要12.56 cm2的硬纸片。
28.26>12.56
四、课堂小结
实际问题 类型 表面积
无盖水桶
薯片盒
压路机前轮
一头封闭的圆柱形物体
侧面积 + 一个底面积
两头封闭的圆柱形物体
侧面积 + 两个底面积
没有底的圆柱形物体
侧面积
