小学数学北师大版六年级下1.6 圆柱的体积(二)课件(共14张PPT)
文档属性
| 名称 | 小学数学北师大版六年级下1.6 圆柱的体积(二)课件(共14张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-26 07:36:14 | ||
图片预览




文档简介
(共14张PPT)
一 圆柱与圆锥
第6课时 圆柱的体积(二)
一、复习引入
圆柱的体积计算方法是怎样的推导出来的?圆柱的体积公式是什么?
V = Sh
圆柱底面积
圆柱的高
底面
半径
二、学习新课
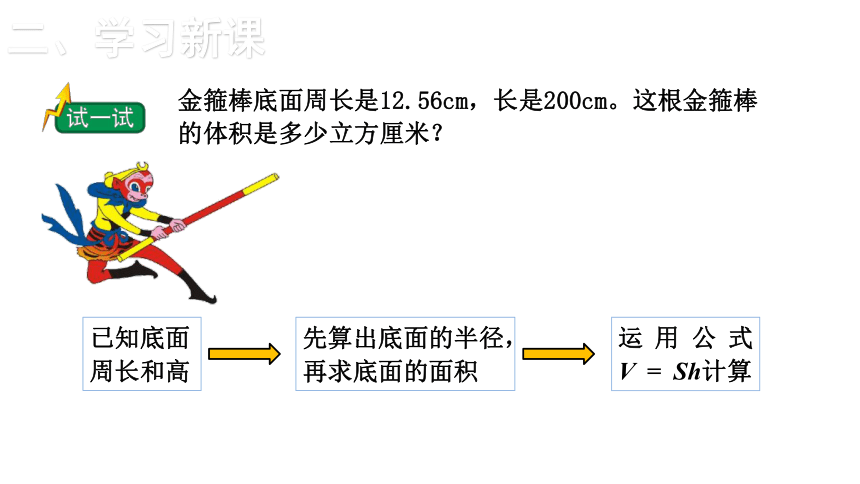
金箍棒底面周长是12.56cm,长是200cm。这根金箍棒的体积是多少立方厘米?
已知底面周长和高
先算出底面的半径,再求底面的面积
运用公式
V = Sh计算
二、学习新课
底面半径:
12.56÷3.14÷2=2(cm)
底面积:
3.14×22=12.56(cm2)
体积:
12.56×200=2512(cm3)
答:这根金箍棒的体积是2512 cm3。
金箍棒底面周长是12.56cm,长是200cm。这根金箍棒的体积是多少立方厘米?
二、学习新课
如果这根金箍棒是铁制的,每立方厘米铁的质量为7.9g,这根金箍棒的质量为多少千克?
7.9×2512=19844.8(g)
答:这根金箍棒的质量为19.8448 kg。
19844.8 g=19.8448 kg
二、学习新课
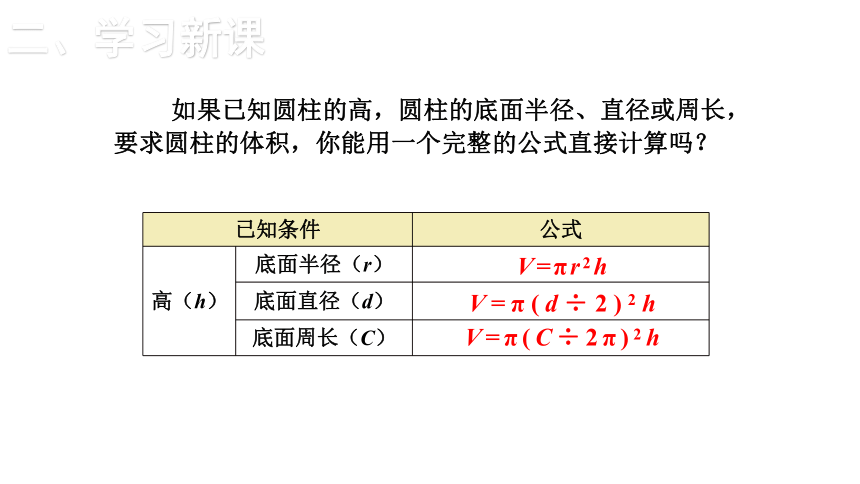
如果已知圆柱的高,圆柱的底面半径、直径或周长,要求圆柱的体积,你能用一个完整的公式直接计算吗?
已知条件 公式
高(h) 底面半径(r)
底面直径(d)
底面周长(C)
V=πr2h
V=π(d÷2)2h
V=π(C÷2π)2h
二、学习新课
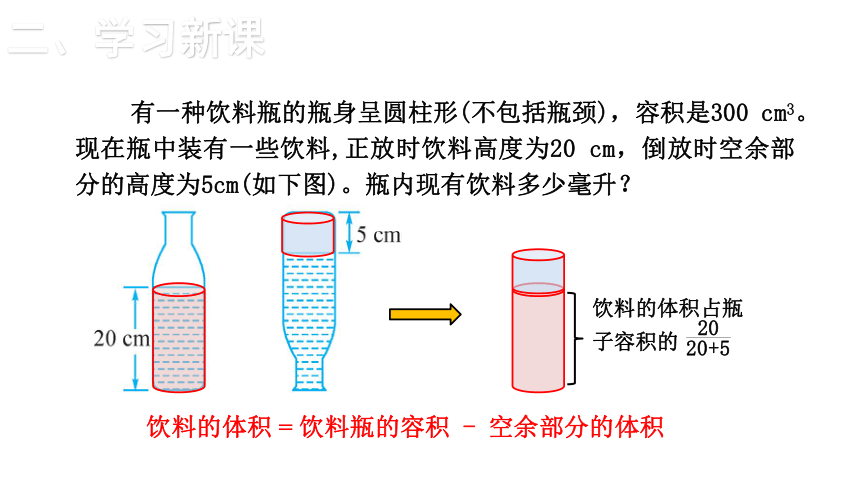
有一种饮料瓶的瓶身呈圆柱形(不包括瓶颈),容积是300 cm3。现在瓶中装有一些饮料,正放时饮料高度为20 cm,倒放时空余部分的高度为5cm(如下图)。瓶内现有饮料多少毫升?
饮料的体积 = 饮料瓶的容积 - 空余部分的体积
饮料的体积占瓶子容积的
二、学习新课
答:瓶内现有饮料240 mL。
240 cm3=240 mL
300× =240(cm3)
有一种饮料瓶的瓶身呈圆柱形(不包括瓶颈),容积是300 cm3。现在瓶中装有一些饮料,正放时饮料高度为20 cm,倒放时空余部分的高度为5cm(如下图)。瓶内现有饮料多少毫升?
二、学习新课
求不规则物体的体积,可以利用体积不变的性质,将其转换为规则图形计算体积。
三、巩固练习
4. 光明村李大伯家挖一口圆柱形的水井,底面周长是3.14 m,深4 m。挖出了多少立方米的土?
3.14×(3.14÷3.14÷2)2×4=3.14(m3)
答:挖出了3.14 m3的土。
三、巩固练习
5.一个装满稻谷的圆柱形粮囤,底面面积为2 m2,高为80 cm。每立方米稻谷的质量约为700 kg,这个粮囤存放的稻谷的质量约为多少千克?
答:这个粮囤存放的稻谷的质量约为1120 kg。
80 cm=0.8 m
2×0.8×700=1120(kg)
三、巩固练习
7.如图,求出小铁块的体积。
2 cm
2 cm
10 cm
3.14×(10÷2)2×2=157(cm3)
10 cm
5 cm
三、巩固练习
9. 寻找日常生活中的三个粗细不同的圆柱形物体。
(1)分别估计它们的体积。
(2)测量相关数据,计算它们的体积。
(3)比较估计值与计算值,哪一种圆柱体的体积你不容易估准
课后分小组练习
四、课堂小结
已知条件 公式
高(h) 底面半径(r)
底面直径(d)
底面周长(C)
V=πr2h
V=π(d÷2)2h
V=π(C÷2π)2h
1.
2.求不规则物体的体积,可以利用体积不变的性质,
将其转换为规则图形计算体积。
一 圆柱与圆锥
第6课时 圆柱的体积(二)
一、复习引入
圆柱的体积计算方法是怎样的推导出来的?圆柱的体积公式是什么?
V = Sh
圆柱底面积
圆柱的高
底面
半径
二、学习新课
金箍棒底面周长是12.56cm,长是200cm。这根金箍棒的体积是多少立方厘米?
已知底面周长和高
先算出底面的半径,再求底面的面积
运用公式
V = Sh计算
二、学习新课
底面半径:
12.56÷3.14÷2=2(cm)
底面积:
3.14×22=12.56(cm2)
体积:
12.56×200=2512(cm3)
答:这根金箍棒的体积是2512 cm3。
金箍棒底面周长是12.56cm,长是200cm。这根金箍棒的体积是多少立方厘米?
二、学习新课
如果这根金箍棒是铁制的,每立方厘米铁的质量为7.9g,这根金箍棒的质量为多少千克?
7.9×2512=19844.8(g)
答:这根金箍棒的质量为19.8448 kg。
19844.8 g=19.8448 kg
二、学习新课
如果已知圆柱的高,圆柱的底面半径、直径或周长,要求圆柱的体积,你能用一个完整的公式直接计算吗?
已知条件 公式
高(h) 底面半径(r)
底面直径(d)
底面周长(C)
V=πr2h
V=π(d÷2)2h
V=π(C÷2π)2h
二、学习新课
有一种饮料瓶的瓶身呈圆柱形(不包括瓶颈),容积是300 cm3。现在瓶中装有一些饮料,正放时饮料高度为20 cm,倒放时空余部分的高度为5cm(如下图)。瓶内现有饮料多少毫升?
饮料的体积 = 饮料瓶的容积 - 空余部分的体积
饮料的体积占瓶子容积的
二、学习新课
答:瓶内现有饮料240 mL。
240 cm3=240 mL
300× =240(cm3)
有一种饮料瓶的瓶身呈圆柱形(不包括瓶颈),容积是300 cm3。现在瓶中装有一些饮料,正放时饮料高度为20 cm,倒放时空余部分的高度为5cm(如下图)。瓶内现有饮料多少毫升?
二、学习新课
求不规则物体的体积,可以利用体积不变的性质,将其转换为规则图形计算体积。
三、巩固练习
4. 光明村李大伯家挖一口圆柱形的水井,底面周长是3.14 m,深4 m。挖出了多少立方米的土?
3.14×(3.14÷3.14÷2)2×4=3.14(m3)
答:挖出了3.14 m3的土。
三、巩固练习
5.一个装满稻谷的圆柱形粮囤,底面面积为2 m2,高为80 cm。每立方米稻谷的质量约为700 kg,这个粮囤存放的稻谷的质量约为多少千克?
答:这个粮囤存放的稻谷的质量约为1120 kg。
80 cm=0.8 m
2×0.8×700=1120(kg)
三、巩固练习
7.如图,求出小铁块的体积。
2 cm
2 cm
10 cm
3.14×(10÷2)2×2=157(cm3)
10 cm
5 cm
三、巩固练习
9. 寻找日常生活中的三个粗细不同的圆柱形物体。
(1)分别估计它们的体积。
(2)测量相关数据,计算它们的体积。
(3)比较估计值与计算值,哪一种圆柱体的体积你不容易估准
课后分小组练习
四、课堂小结
已知条件 公式
高(h) 底面半径(r)
底面直径(d)
底面周长(C)
V=πr2h
V=π(d÷2)2h
V=π(C÷2π)2h
1.
2.求不规则物体的体积,可以利用体积不变的性质,
将其转换为规则图形计算体积。
