2021-2022学年苏科版九年级数学下册6.3相似图形 同步强化训练 (word版含答案)
文档属性
| 名称 | 2021-2022学年苏科版九年级数学下册6.3相似图形 同步强化训练 (word版含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 584.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-26 00:00:00 | ||
图片预览

文档简介
2021-2022学年苏科版九年级下《6.3相似图形》同步强化训练
(时间:90分钟 满分:120分)
一.选择题(共36分)
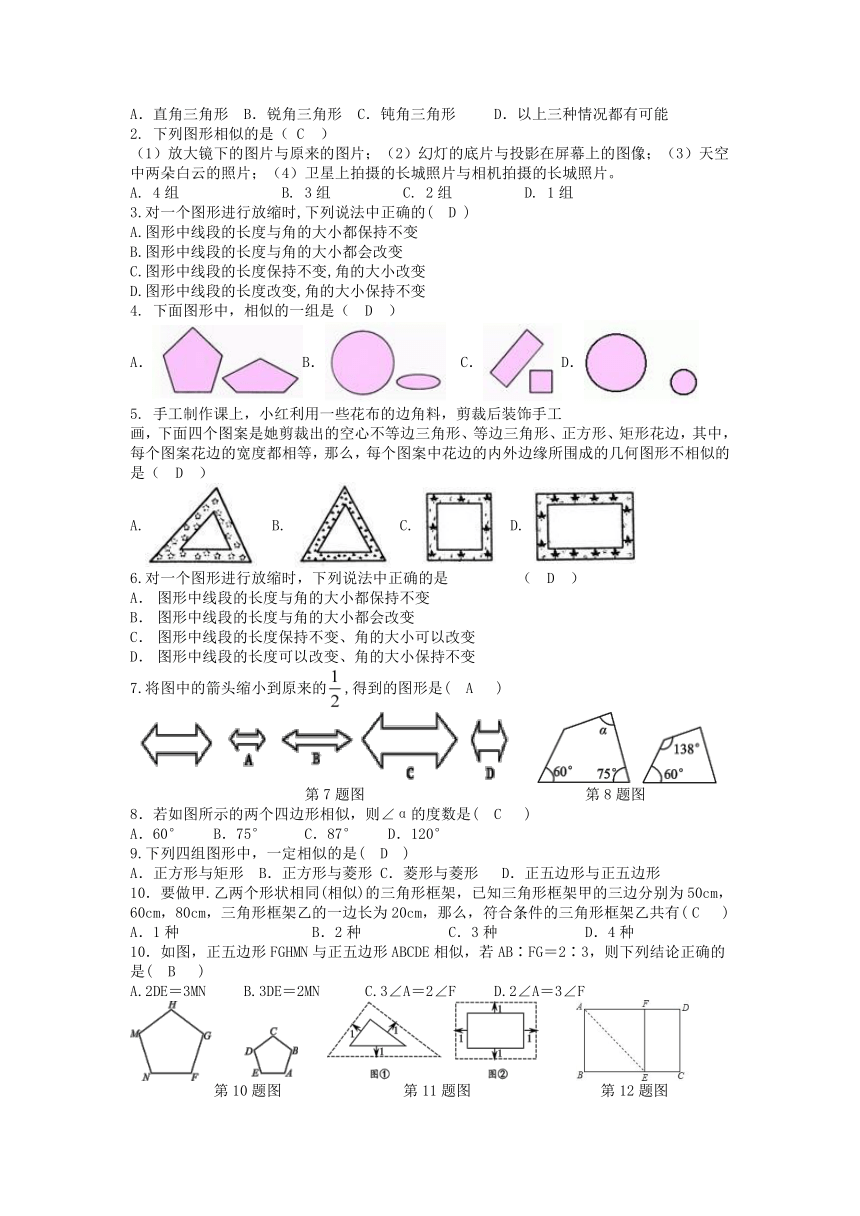
1.将一个直角三角形三边扩大3倍,得到的三角形一定是( )
A.直角三角形 B.锐角三角形 C.钝角三角形 D.以上三种情况都有可能
2. 下列图形相似的是( )
(1)放大镜下的图片与原来的图片;(2)幻灯的底片与投影在屏幕上的图像;(3)天空中两朵白云的照片;(4)卫星上拍摄的长城照片与相机拍摄的长城照片。
A. 4组 B. 3组 C. 2组 D. 1组
3.对一个图形进行放缩时,下列说法中正确的( )
A.图形中线段的长度与角的大小都保持不变
B.图形中线段的长度与角的大小都会改变
C.图形中线段的长度保持不变,角的大小改变
D.图形中线段的长度改变,角的大小保持不变
4. 下面图形中,相似的一组是( )
A.B. C.D.
5. 手工制作课上,小红利用一些花布的边角料,剪裁后装饰手工
画,下面四个图案是她剪裁出的空心不等边三角形、等边三角形、正方形、矩形花边,其中,每个图案花边的宽度都相等,那么,每个图案中花边的内外边缘所围成的几何图形不相似的是( )
A. B. C. D.
6.对一个图形进行放缩时,下列说法中正确的是( )
A. 图形中线段的长度与角的大小都保持不变
B. 图形中线段的长度与角的大小都会改变
C. 图形中线段的长度保持不变、角的大小可以改变
D. 图形中线段的长度可以改变、角的大小保持不变
7.将图中的箭头缩小到原来的,得到的图形是( )
第7题图 第8题图
8.若如图所示的两个四边形相似,则∠α的度数是( )
A.60° B.75° C.87° D.120°
9.下列四组图形中,一定相似的是( )
A.正方形与矩形 B.正方形与菱形 C.菱形与菱形 D.正五边形与正五边形
10.要做甲.乙两个形状相同(相似)的三角形框架,已知三角形框架甲的三边分别为50cm,60cm,80cm,三角形框架乙的一边长为20cm,那么,符合条件的三角形框架乙共有( )
A.1种 B.2种 C.3种 D.4种
10.如图,正五边形FGHMN与正五边形ABCDE相似,若AB∶FG=2∶3,则下列结论正确的是( )
A.2DE=3MN B.3DE=2MN C.3∠A=2∠F D.2∠A=3∠F
第10题图 第11题图 第12题图
11.在研究相似问题时,甲、乙两同学的观点如下:甲:将边长为3,4,5的三角形按图①的方式向外扩张,得到新三角形,它们的对应边间距均为1,则新三角形与原三角形相似.
乙:将邻边为3和5的矩形按图②的方式向外扩张,得到新的矩形,它们的对应边间距均为1,则新矩形与原矩形不相似.对于两人的观点,下列说法正确的是( )
A.两人都对 B.两人都不对 C.甲对,乙不对 D.甲不对,乙对
12.已知矩形ABCD中,AB=1,在BC上取一点E,沿AE将△ABE向上折
叠,使B点落在AD上的F点,若四边形EFDC与矩形ABCD相似,则AD= ( )
A. B. C. D.2
二.填空题(共24分)
13. 用“正确”与“错误”填空:
(1)所有的三角形都相似_________; (2)所有的梯形都相似__________;
(3)所有的等腰三角形都相似_______; (4)所有的直角三角形都相似_________;
(5)所有的矩形都相似_________; (6)所有的平行四边形都相似_______;
(7)大小的中国地图相似_________; (8)所有的正多边形都相似_________.
14.下列情形:①用眼睛看月亮和用望远镜看月亮,看到的图像是相似的图形;②用彩笔在黑板上写上三个大字1、2、3,它们是相似图形;③用粉笔在黑板上写上“天”和用毛笔在纸上写上“天”,这两个字是相似图形;以上说法你认为正确的是__________,错误的是__________。(填序号)
15.下列图形中是_________与_______相似的.
(1)(2)(3)(4)
第15题图 第16题图
16.如图,相似的正方形共有 个,相似的三角形共有 个.
17.有一块三角形的草地,它的一条边长为25.在图纸上,这条边的长为5,其他两条边的长都为4,则其他两边的实际长度都是 .
18. △ABC中,D、E分别在AB、AC上,DE∥BC,△ADE是△ABC缩小后的图形.若DE把△ABC的面积分成相等的两部分,则AD:AB=________.
19.把一矩形纸片对折,如果对折后的矩形与原矩形相似,则原矩
形纸片的长与宽之比为____________.
第19题 第20题
20.如图(1),将一个正六边形各边延长,构成一个正六角星形AFBDCE,
它的面积为1,取△ABC和△DEF各边中点,连接成正六角星形A1F1B1D1C1E1,如图(2)中阴影部分,取△A1B1C1和△D1E1F1各边中点,连接成正六角星形A2F2B2D2C2E2,如图(3)中阴影部分,如此下去…,则正六角星形A4F4B4D4C4E4的面积为______.
三.解答题(共60分)
21.(6分)如图在格点图中画出所给图形的相似形,使新图形的各顶点仍然在格点上.
22.(6分)如图,矩形的两邻边长的和等于a cm,将这两邻边分别延长m cm,n cm(m>n),所得的新矩形与原矩形相似,求原矩形的两邻边的长.
23.(6分)已知△ABC∽△A′B′C′,且△ABC的三边长之比为3∶5∶7,而△A′B′C′的最大边长为15 cm,求△A′B′C′的周长.
24.(6分)如图,G是正方形ABCD对角线AC上一点,作GE⊥AD,GF⊥AB,垂足分别为点E,F.求证:四边形AFGE与四边形ABCD相似.
25.(8分)如图,把矩形ABCD对折,折痕为MN,矩形DMNC与矩形ABCD相似,已知AB=4.
(1)求AD的长;
(2)求矩形DMNC与矩形ABCD的相似比.
26.(8分)如图,梯形ABCD与梯形A′B′C′D′相似,AD∥BC,A′D′∥B′C′,∠A=∠A′.AD=4,A′D′=6,AB=6,B′C′=12.求: (1)梯形ABCD与梯形A′B′C′D′的相似比k;(2)A′B′和BC的长;(3)D′C′∶DC.
27.(10分)如图所示,在矩形ABCD中,AB=10,AD=20,两只小虫P和Q同时分别从A,B出发沿AB,BC向终点B,C方向前进,小虫P每秒走1,小虫Q每秒走2,请问它们同时出发多少秒时,以P、B、Q为顶点的三角形与以A、C、D为顶点的三角形相似?
28.(10分)分类讨论如图,矩形ABCD的长AB=30,宽BC=20.
(1)如图①,若沿矩形ABCD四周有宽为1的环形区域,图中所形成的两个矩形,即矩形ABCD与矩形A′B′C′D′相似吗?请说明理由;
(2)如图②,x为多少时,图中的两个矩形,即矩形ABCD与矩形A′B′C′D′相似?
教师样卷
一.选择题(共36分)
1.将一个直角三角形三边扩大3倍,得到的三角形一定是( A )
A.直角三角形 B.锐角三角形 C.钝角三角形 D.以上三种情况都有可能
2. 下列图形相似的是( C )
(1)放大镜下的图片与原来的图片;(2)幻灯的底片与投影在屏幕上的图像;(3)天空中两朵白云的照片;(4)卫星上拍摄的长城照片与相机拍摄的长城照片。
A. 4组 B. 3组 C. 2组 D. 1组
3.对一个图形进行放缩时,下列说法中正确的( D )
A.图形中线段的长度与角的大小都保持不变
B.图形中线段的长度与角的大小都会改变
C.图形中线段的长度保持不变,角的大小改变
D.图形中线段的长度改变,角的大小保持不变
4. 下面图形中,相似的一组是( D )
A.B. C.D.
5. 手工制作课上,小红利用一些花布的边角料,剪裁后装饰手工
画,下面四个图案是她剪裁出的空心不等边三角形、等边三角形、正方形、矩形花边,其中,每个图案花边的宽度都相等,那么,每个图案中花边的内外边缘所围成的几何图形不相似的是( D )
A. B. C. D.
6.对一个图形进行放缩时,下列说法中正确的是 ( D )
A. 图形中线段的长度与角的大小都保持不变
B. 图形中线段的长度与角的大小都会改变
C. 图形中线段的长度保持不变、角的大小可以改变
D. 图形中线段的长度可以改变、角的大小保持不变
7.将图中的箭头缩小到原来的,得到的图形是( A )
第7题图 第8题图
8.若如图所示的两个四边形相似,则∠α的度数是( C )
A.60° B.75° C.87° D.120°
9.下列四组图形中,一定相似的是( D )
A.正方形与矩形 B.正方形与菱形 C.菱形与菱形 D.正五边形与正五边形
10.要做甲.乙两个形状相同(相似)的三角形框架,已知三角形框架甲的三边分别为50cm,60cm,80cm,三角形框架乙的一边长为20cm,那么,符合条件的三角形框架乙共有( C )
A.1种 B.2种 C.3种 D.4种
10.如图,正五边形FGHMN与正五边形ABCDE相似,若AB∶FG=2∶3,则下列结论正确的是( B )
A.2DE=3MN B.3DE=2MN C.3∠A=2∠F D.2∠A=3∠F
第10题图 第11题图 第12题图
11.在研究相似问题时,甲、乙两同学的观点如下:甲:将边长为3,4,5的三角形按图①的方式向外扩张,得到新三角形,它们的对应边间距均为1,则新三角形与原三角形相似.
乙:将邻边为3和5的矩形按图②的方式向外扩张,得到新的矩形,它们的对应边间距均为1,则新矩形与原矩形不相似.对于两人的观点,下列说法正确的是( A )
A.两人都对 B.两人都不对 C.甲对,乙不对 D.甲不对,乙对
12.已知矩形ABCD中,AB=1,在BC上取一点E,沿AE将△ABE向上折
叠,使B点落在AD上的F点,若四边形EFDC与矩形ABCD相似,则AD= ( B )
A. B. C. D.2
二.填空题(共24分)
13. 用“正确”与“错误”填空:
(1)所有的三角形都相似_________; (2)所有的梯形都相似__________;
(3)所有的等腰三角形都相似_______; (4)所有的直角三角形都相似_________;
(5)所有的矩形都相似_________; (6)所有的平行四边形都相似_______;
(7)大小的中国地图相似_________; (8)所有的正多边形都相似_________.
【答案】(1)错误,(2)错误,(3)错误,(4)错误,(5)错误,(6)错误,(7)正确,(8)错误.
14.下列情形:①用眼睛看月亮和用望远镜看月亮,看到的图像是相似的图形;②用彩笔在黑板上写上三个大字1、2、3,它们是相似图形;③用粉笔在黑板上写上“天”和用毛笔在纸上写上“天”,这两个字是相似图形;以上说法你认为正确的是__________,错误的是__________。(填序号)
【答案】.①,②③
15.下列图形中是_________与_______相似的.
【答案】图形中是(1)与(4)相似的.
(2)(2)(3)(4)
第15题图 第16题图
16.如图,相似的正方形共有 个,相似的三角形共有 个.
【答案】5 16
17.有一块三角形的草地,它的一条边长为25.在图纸上,这条边的长为5,其他两条边的长都为4,则其他两边的实际长度都是 .
【答案】20.【解析】设其他两边的实际长度分别为、,由题意得,,
解得.即其他两边的实际长度都是20.
19. △ABC中,D、E分别在AB、AC上,DE∥BC,△ADE是△ABC缩小后的图形.若DE把△ABC的面积分成相等的两部分,则AD:AB=________.
【答案】 ;
19.把一矩形纸片对折,如果对折后的矩形与原矩形相似,则原矩
形纸片的长与宽之比为____________.
【答案】; 【解析】矩形ABCD对折后所得矩形与原矩形相似,则矩形ABCD∽矩形BFEA,设矩形的长为,宽为.则AB=CD=,AD=BC=,BF=AE=,根据矩形相似,对应边的比相等得到:即:,则b2=∴∴
第19题 第20题
20.如图(1),将一个正六边形各边延长,构成一个正六角星形AFBDCE,
它的面积为1,取△ABC和△DEF各边中点,连接成正六角星形A1F1B1D1C1E1,如图(2)中阴影部分,取△A1B1C1和△D1E1F1各边中点,连接成正六角星形A2F2B2D2C2E2,如图(3)中阴影部分,如此下去…,则正六角星形A4F4B4D4C4E4的面积为______.
【答案】.【解析】∵A1、F1、B1、D1、C1、E1分别是△ABC和△DEF各边中点,∴正六角星形AFBDCE∽正六角星形A1F1B1D1C1E1,且相似比为2:1,∵正六角星形AFBDCE的面积为1,∴正六角星形A1F1B1D1C1E1的面积为,同理可得,第三个六角形的面积为:=,
第四个六角形的面积为:,故答案为:.
三.解答题(共60分)
21.(6分)如图在格点图中画出所给图形的相似形,使新图形的各顶点仍然在格点上.
[解析] 把每条线段都放大到相同的倍数,如2倍,并保持各个角度不变.
解:答案不唯一.如图所示.
22.(6分)如图,矩形的两邻边长的和等于a cm,将这两邻边分别延长m cm,n cm(m>n),所得的新矩形与原矩形相似,求原矩形的两邻边的长.
[解析] 新矩形与原矩形相似,可得原矩形的一组邻边的比为m∶n,从而可得两邻边的长.
解:设原矩形的一组邻边的长分别为x cm,y cm(x>y),则=,∴=,∴=.
又∵x+y=a,∴=,∴y=,同理可得x=.即原矩形的两邻边的长分别为 cm, cm.
23.(6分)已知△ABC∽△A′B′C′,且△ABC的三边长之比为3∶5∶7,而△A′B′C′的最大边长为15 cm,求△A′B′C′的周长.
解:由△ABC∽△A′B′C′,可得==.又因为△ABC三边长的比为3∶5∶7,不妨设AB∶AC∶BC=3∶5∶7.故A′B′∶A′C′∶B′C′=3∶5∶7.
又有B′C′=15 cm,易求出A′B′= cm,A′C′= cm,所以△A′B′C′的周长为15++=(cm).
24.(6分)如图,G是正方形ABCD对角线AC上一点,作GE⊥AD,GF⊥AB,垂足分别为点E,F.求证:四边形AFGE与四边形ABCD相似.
证明:∵四边形ABCD是正方形,AC是对角线,∴∠DAC=∠BAC=45°.又∵GE⊥AD,GF⊥AB,∴EG=FG,且AE=EG,AF=FG.∴AE=EG=FG=AF.又∵∠EAF=90°,∴四边形AFGE为正方形.∴===,且∠EAF=∠DAB,∠AFG=∠ABC,∠FGE=∠BCD,∠AEG=∠ADC.∴四边形AFGE与四边形ABCD相似.
25.(8分)如图,把矩形ABCD对折,折痕为MN,矩形DMNC与矩形ABCD相似,已知AB=4.
(1)求AD的长;
(2)求矩形DMNC与矩形ABCD的相似比.
解:(1)设AD=x(x>0),则DM=.∵矩形DMNC与矩形ABCD相似,∴=,
即=.解得x=4(舍负).∴AD的长为4.
(2)矩形DMNC与矩形ABCD的相似比为==.
26.(8分)如图,梯形ABCD与梯形A′B′C′D′相似,AD∥BC,A′D′∥B′C′,∠A=∠A′.AD=4,A′D′=6,AB=6,B′C′=12.求: (1)梯形ABCD与梯形A′B′C′D′的相似比k;(2)A′B′和BC的长;(3)D′C′∶DC.
解:(1)相似比k=AD∶A′D′=4∶6=2∶3;
(2)根据题意,得A′B′的对应边是AB,BC的对应边是B′C′,∴k=AB∶A′B′=BC∶B′C′,即2∶3=6∶A′B′,2∶3=BC∶12.解得A′B′=9,BC=8;
(3)∵k=CD∶C′D′=2∶3,∴D′C′∶DC=3∶2.
27.(10分)如图所示,在矩形ABCD中,AB=10,AD=20,两只小虫P和Q同时分别从A,B出发沿AB,BC向终点B,C方向前进,小虫P每秒走1,小虫Q每秒走2,请问它们同时出发多少秒时,以P、B、Q为顶点的三角形与以A、C、D为顶点的三角形相似?
解:①设经秒后,△PBQ∽△CDA,由于∠PBQ=∠ADC=90°,当时,
即,解得;
②设经秒后,△QBP∽△CDA, 由于∠PBQ=∠ADC=90°,当,
即,解得.故经过5秒或2秒时,以P、B、Q为顶点的三角形与以A、C、D为顶点的三角形相似.
28.(10分)分类讨论如图,矩形ABCD的长AB=30,宽BC=20.
(1)如图①,若沿矩形ABCD四周有宽为1的环形区域,图中所形成的两个矩形,即矩形ABCD与矩形A′B′C′D′相似吗?请说明理由;
(2)如图②,x为多少时,图中的两个矩形,即矩形ABCD与矩形A′B′C′D′相似?
解:(1)不相似.
理由:因为AB=30,A′B′=28,BC=20,B′C′=18,而≠,
所以矩形ABCD与矩形A′B′C′D′不相似.
(2)若矩形ABCD与矩形A′B′C′D′相似,则=或=,
则=或=,
解得x=1.5或x=9.
故当x为1.5或9时,矩形ABCD与矩形A′B′C′D′相似.
(时间:90分钟 满分:120分)
一.选择题(共36分)
1.将一个直角三角形三边扩大3倍,得到的三角形一定是( )
A.直角三角形 B.锐角三角形 C.钝角三角形 D.以上三种情况都有可能
2. 下列图形相似的是( )
(1)放大镜下的图片与原来的图片;(2)幻灯的底片与投影在屏幕上的图像;(3)天空中两朵白云的照片;(4)卫星上拍摄的长城照片与相机拍摄的长城照片。
A. 4组 B. 3组 C. 2组 D. 1组
3.对一个图形进行放缩时,下列说法中正确的( )
A.图形中线段的长度与角的大小都保持不变
B.图形中线段的长度与角的大小都会改变
C.图形中线段的长度保持不变,角的大小改变
D.图形中线段的长度改变,角的大小保持不变
4. 下面图形中,相似的一组是( )
A.B. C.D.
5. 手工制作课上,小红利用一些花布的边角料,剪裁后装饰手工
画,下面四个图案是她剪裁出的空心不等边三角形、等边三角形、正方形、矩形花边,其中,每个图案花边的宽度都相等,那么,每个图案中花边的内外边缘所围成的几何图形不相似的是( )
A. B. C. D.
6.对一个图形进行放缩时,下列说法中正确的是( )
A. 图形中线段的长度与角的大小都保持不变
B. 图形中线段的长度与角的大小都会改变
C. 图形中线段的长度保持不变、角的大小可以改变
D. 图形中线段的长度可以改变、角的大小保持不变
7.将图中的箭头缩小到原来的,得到的图形是( )
第7题图 第8题图
8.若如图所示的两个四边形相似,则∠α的度数是( )
A.60° B.75° C.87° D.120°
9.下列四组图形中,一定相似的是( )
A.正方形与矩形 B.正方形与菱形 C.菱形与菱形 D.正五边形与正五边形
10.要做甲.乙两个形状相同(相似)的三角形框架,已知三角形框架甲的三边分别为50cm,60cm,80cm,三角形框架乙的一边长为20cm,那么,符合条件的三角形框架乙共有( )
A.1种 B.2种 C.3种 D.4种
10.如图,正五边形FGHMN与正五边形ABCDE相似,若AB∶FG=2∶3,则下列结论正确的是( )
A.2DE=3MN B.3DE=2MN C.3∠A=2∠F D.2∠A=3∠F
第10题图 第11题图 第12题图
11.在研究相似问题时,甲、乙两同学的观点如下:甲:将边长为3,4,5的三角形按图①的方式向外扩张,得到新三角形,它们的对应边间距均为1,则新三角形与原三角形相似.
乙:将邻边为3和5的矩形按图②的方式向外扩张,得到新的矩形,它们的对应边间距均为1,则新矩形与原矩形不相似.对于两人的观点,下列说法正确的是( )
A.两人都对 B.两人都不对 C.甲对,乙不对 D.甲不对,乙对
12.已知矩形ABCD中,AB=1,在BC上取一点E,沿AE将△ABE向上折
叠,使B点落在AD上的F点,若四边形EFDC与矩形ABCD相似,则AD= ( )
A. B. C. D.2
二.填空题(共24分)
13. 用“正确”与“错误”填空:
(1)所有的三角形都相似_________; (2)所有的梯形都相似__________;
(3)所有的等腰三角形都相似_______; (4)所有的直角三角形都相似_________;
(5)所有的矩形都相似_________; (6)所有的平行四边形都相似_______;
(7)大小的中国地图相似_________; (8)所有的正多边形都相似_________.
14.下列情形:①用眼睛看月亮和用望远镜看月亮,看到的图像是相似的图形;②用彩笔在黑板上写上三个大字1、2、3,它们是相似图形;③用粉笔在黑板上写上“天”和用毛笔在纸上写上“天”,这两个字是相似图形;以上说法你认为正确的是__________,错误的是__________。(填序号)
15.下列图形中是_________与_______相似的.
(1)(2)(3)(4)
第15题图 第16题图
16.如图,相似的正方形共有 个,相似的三角形共有 个.
17.有一块三角形的草地,它的一条边长为25.在图纸上,这条边的长为5,其他两条边的长都为4,则其他两边的实际长度都是 .
18. △ABC中,D、E分别在AB、AC上,DE∥BC,△ADE是△ABC缩小后的图形.若DE把△ABC的面积分成相等的两部分,则AD:AB=________.
19.把一矩形纸片对折,如果对折后的矩形与原矩形相似,则原矩
形纸片的长与宽之比为____________.
第19题 第20题
20.如图(1),将一个正六边形各边延长,构成一个正六角星形AFBDCE,
它的面积为1,取△ABC和△DEF各边中点,连接成正六角星形A1F1B1D1C1E1,如图(2)中阴影部分,取△A1B1C1和△D1E1F1各边中点,连接成正六角星形A2F2B2D2C2E2,如图(3)中阴影部分,如此下去…,则正六角星形A4F4B4D4C4E4的面积为______.
三.解答题(共60分)
21.(6分)如图在格点图中画出所给图形的相似形,使新图形的各顶点仍然在格点上.
22.(6分)如图,矩形的两邻边长的和等于a cm,将这两邻边分别延长m cm,n cm(m>n),所得的新矩形与原矩形相似,求原矩形的两邻边的长.
23.(6分)已知△ABC∽△A′B′C′,且△ABC的三边长之比为3∶5∶7,而△A′B′C′的最大边长为15 cm,求△A′B′C′的周长.
24.(6分)如图,G是正方形ABCD对角线AC上一点,作GE⊥AD,GF⊥AB,垂足分别为点E,F.求证:四边形AFGE与四边形ABCD相似.
25.(8分)如图,把矩形ABCD对折,折痕为MN,矩形DMNC与矩形ABCD相似,已知AB=4.
(1)求AD的长;
(2)求矩形DMNC与矩形ABCD的相似比.
26.(8分)如图,梯形ABCD与梯形A′B′C′D′相似,AD∥BC,A′D′∥B′C′,∠A=∠A′.AD=4,A′D′=6,AB=6,B′C′=12.求: (1)梯形ABCD与梯形A′B′C′D′的相似比k;(2)A′B′和BC的长;(3)D′C′∶DC.
27.(10分)如图所示,在矩形ABCD中,AB=10,AD=20,两只小虫P和Q同时分别从A,B出发沿AB,BC向终点B,C方向前进,小虫P每秒走1,小虫Q每秒走2,请问它们同时出发多少秒时,以P、B、Q为顶点的三角形与以A、C、D为顶点的三角形相似?
28.(10分)分类讨论如图,矩形ABCD的长AB=30,宽BC=20.
(1)如图①,若沿矩形ABCD四周有宽为1的环形区域,图中所形成的两个矩形,即矩形ABCD与矩形A′B′C′D′相似吗?请说明理由;
(2)如图②,x为多少时,图中的两个矩形,即矩形ABCD与矩形A′B′C′D′相似?
教师样卷
一.选择题(共36分)
1.将一个直角三角形三边扩大3倍,得到的三角形一定是( A )
A.直角三角形 B.锐角三角形 C.钝角三角形 D.以上三种情况都有可能
2. 下列图形相似的是( C )
(1)放大镜下的图片与原来的图片;(2)幻灯的底片与投影在屏幕上的图像;(3)天空中两朵白云的照片;(4)卫星上拍摄的长城照片与相机拍摄的长城照片。
A. 4组 B. 3组 C. 2组 D. 1组
3.对一个图形进行放缩时,下列说法中正确的( D )
A.图形中线段的长度与角的大小都保持不变
B.图形中线段的长度与角的大小都会改变
C.图形中线段的长度保持不变,角的大小改变
D.图形中线段的长度改变,角的大小保持不变
4. 下面图形中,相似的一组是( D )
A.B. C.D.
5. 手工制作课上,小红利用一些花布的边角料,剪裁后装饰手工
画,下面四个图案是她剪裁出的空心不等边三角形、等边三角形、正方形、矩形花边,其中,每个图案花边的宽度都相等,那么,每个图案中花边的内外边缘所围成的几何图形不相似的是( D )
A. B. C. D.
6.对一个图形进行放缩时,下列说法中正确的是 ( D )
A. 图形中线段的长度与角的大小都保持不变
B. 图形中线段的长度与角的大小都会改变
C. 图形中线段的长度保持不变、角的大小可以改变
D. 图形中线段的长度可以改变、角的大小保持不变
7.将图中的箭头缩小到原来的,得到的图形是( A )
第7题图 第8题图
8.若如图所示的两个四边形相似,则∠α的度数是( C )
A.60° B.75° C.87° D.120°
9.下列四组图形中,一定相似的是( D )
A.正方形与矩形 B.正方形与菱形 C.菱形与菱形 D.正五边形与正五边形
10.要做甲.乙两个形状相同(相似)的三角形框架,已知三角形框架甲的三边分别为50cm,60cm,80cm,三角形框架乙的一边长为20cm,那么,符合条件的三角形框架乙共有( C )
A.1种 B.2种 C.3种 D.4种
10.如图,正五边形FGHMN与正五边形ABCDE相似,若AB∶FG=2∶3,则下列结论正确的是( B )
A.2DE=3MN B.3DE=2MN C.3∠A=2∠F D.2∠A=3∠F
第10题图 第11题图 第12题图
11.在研究相似问题时,甲、乙两同学的观点如下:甲:将边长为3,4,5的三角形按图①的方式向外扩张,得到新三角形,它们的对应边间距均为1,则新三角形与原三角形相似.
乙:将邻边为3和5的矩形按图②的方式向外扩张,得到新的矩形,它们的对应边间距均为1,则新矩形与原矩形不相似.对于两人的观点,下列说法正确的是( A )
A.两人都对 B.两人都不对 C.甲对,乙不对 D.甲不对,乙对
12.已知矩形ABCD中,AB=1,在BC上取一点E,沿AE将△ABE向上折
叠,使B点落在AD上的F点,若四边形EFDC与矩形ABCD相似,则AD= ( B )
A. B. C. D.2
二.填空题(共24分)
13. 用“正确”与“错误”填空:
(1)所有的三角形都相似_________; (2)所有的梯形都相似__________;
(3)所有的等腰三角形都相似_______; (4)所有的直角三角形都相似_________;
(5)所有的矩形都相似_________; (6)所有的平行四边形都相似_______;
(7)大小的中国地图相似_________; (8)所有的正多边形都相似_________.
【答案】(1)错误,(2)错误,(3)错误,(4)错误,(5)错误,(6)错误,(7)正确,(8)错误.
14.下列情形:①用眼睛看月亮和用望远镜看月亮,看到的图像是相似的图形;②用彩笔在黑板上写上三个大字1、2、3,它们是相似图形;③用粉笔在黑板上写上“天”和用毛笔在纸上写上“天”,这两个字是相似图形;以上说法你认为正确的是__________,错误的是__________。(填序号)
【答案】.①,②③
15.下列图形中是_________与_______相似的.
【答案】图形中是(1)与(4)相似的.
(2)(2)(3)(4)
第15题图 第16题图
16.如图,相似的正方形共有 个,相似的三角形共有 个.
【答案】5 16
17.有一块三角形的草地,它的一条边长为25.在图纸上,这条边的长为5,其他两条边的长都为4,则其他两边的实际长度都是 .
【答案】20.【解析】设其他两边的实际长度分别为、,由题意得,,
解得.即其他两边的实际长度都是20.
19. △ABC中,D、E分别在AB、AC上,DE∥BC,△ADE是△ABC缩小后的图形.若DE把△ABC的面积分成相等的两部分,则AD:AB=________.
【答案】 ;
19.把一矩形纸片对折,如果对折后的矩形与原矩形相似,则原矩
形纸片的长与宽之比为____________.
【答案】; 【解析】矩形ABCD对折后所得矩形与原矩形相似,则矩形ABCD∽矩形BFEA,设矩形的长为,宽为.则AB=CD=,AD=BC=,BF=AE=,根据矩形相似,对应边的比相等得到:即:,则b2=∴∴
第19题 第20题
20.如图(1),将一个正六边形各边延长,构成一个正六角星形AFBDCE,
它的面积为1,取△ABC和△DEF各边中点,连接成正六角星形A1F1B1D1C1E1,如图(2)中阴影部分,取△A1B1C1和△D1E1F1各边中点,连接成正六角星形A2F2B2D2C2E2,如图(3)中阴影部分,如此下去…,则正六角星形A4F4B4D4C4E4的面积为______.
【答案】.【解析】∵A1、F1、B1、D1、C1、E1分别是△ABC和△DEF各边中点,∴正六角星形AFBDCE∽正六角星形A1F1B1D1C1E1,且相似比为2:1,∵正六角星形AFBDCE的面积为1,∴正六角星形A1F1B1D1C1E1的面积为,同理可得,第三个六角形的面积为:=,
第四个六角形的面积为:,故答案为:.
三.解答题(共60分)
21.(6分)如图在格点图中画出所给图形的相似形,使新图形的各顶点仍然在格点上.
[解析] 把每条线段都放大到相同的倍数,如2倍,并保持各个角度不变.
解:答案不唯一.如图所示.
22.(6分)如图,矩形的两邻边长的和等于a cm,将这两邻边分别延长m cm,n cm(m>n),所得的新矩形与原矩形相似,求原矩形的两邻边的长.
[解析] 新矩形与原矩形相似,可得原矩形的一组邻边的比为m∶n,从而可得两邻边的长.
解:设原矩形的一组邻边的长分别为x cm,y cm(x>y),则=,∴=,∴=.
又∵x+y=a,∴=,∴y=,同理可得x=.即原矩形的两邻边的长分别为 cm, cm.
23.(6分)已知△ABC∽△A′B′C′,且△ABC的三边长之比为3∶5∶7,而△A′B′C′的最大边长为15 cm,求△A′B′C′的周长.
解:由△ABC∽△A′B′C′,可得==.又因为△ABC三边长的比为3∶5∶7,不妨设AB∶AC∶BC=3∶5∶7.故A′B′∶A′C′∶B′C′=3∶5∶7.
又有B′C′=15 cm,易求出A′B′= cm,A′C′= cm,所以△A′B′C′的周长为15++=(cm).
24.(6分)如图,G是正方形ABCD对角线AC上一点,作GE⊥AD,GF⊥AB,垂足分别为点E,F.求证:四边形AFGE与四边形ABCD相似.
证明:∵四边形ABCD是正方形,AC是对角线,∴∠DAC=∠BAC=45°.又∵GE⊥AD,GF⊥AB,∴EG=FG,且AE=EG,AF=FG.∴AE=EG=FG=AF.又∵∠EAF=90°,∴四边形AFGE为正方形.∴===,且∠EAF=∠DAB,∠AFG=∠ABC,∠FGE=∠BCD,∠AEG=∠ADC.∴四边形AFGE与四边形ABCD相似.
25.(8分)如图,把矩形ABCD对折,折痕为MN,矩形DMNC与矩形ABCD相似,已知AB=4.
(1)求AD的长;
(2)求矩形DMNC与矩形ABCD的相似比.
解:(1)设AD=x(x>0),则DM=.∵矩形DMNC与矩形ABCD相似,∴=,
即=.解得x=4(舍负).∴AD的长为4.
(2)矩形DMNC与矩形ABCD的相似比为==.
26.(8分)如图,梯形ABCD与梯形A′B′C′D′相似,AD∥BC,A′D′∥B′C′,∠A=∠A′.AD=4,A′D′=6,AB=6,B′C′=12.求: (1)梯形ABCD与梯形A′B′C′D′的相似比k;(2)A′B′和BC的长;(3)D′C′∶DC.
解:(1)相似比k=AD∶A′D′=4∶6=2∶3;
(2)根据题意,得A′B′的对应边是AB,BC的对应边是B′C′,∴k=AB∶A′B′=BC∶B′C′,即2∶3=6∶A′B′,2∶3=BC∶12.解得A′B′=9,BC=8;
(3)∵k=CD∶C′D′=2∶3,∴D′C′∶DC=3∶2.
27.(10分)如图所示,在矩形ABCD中,AB=10,AD=20,两只小虫P和Q同时分别从A,B出发沿AB,BC向终点B,C方向前进,小虫P每秒走1,小虫Q每秒走2,请问它们同时出发多少秒时,以P、B、Q为顶点的三角形与以A、C、D为顶点的三角形相似?
解:①设经秒后,△PBQ∽△CDA,由于∠PBQ=∠ADC=90°,当时,
即,解得;
②设经秒后,△QBP∽△CDA, 由于∠PBQ=∠ADC=90°,当,
即,解得.故经过5秒或2秒时,以P、B、Q为顶点的三角形与以A、C、D为顶点的三角形相似.
28.(10分)分类讨论如图,矩形ABCD的长AB=30,宽BC=20.
(1)如图①,若沿矩形ABCD四周有宽为1的环形区域,图中所形成的两个矩形,即矩形ABCD与矩形A′B′C′D′相似吗?请说明理由;
(2)如图②,x为多少时,图中的两个矩形,即矩形ABCD与矩形A′B′C′D′相似?
解:(1)不相似.
理由:因为AB=30,A′B′=28,BC=20,B′C′=18,而≠,
所以矩形ABCD与矩形A′B′C′D′不相似.
(2)若矩形ABCD与矩形A′B′C′D′相似,则=或=,
则=或=,
解得x=1.5或x=9.
故当x为1.5或9时,矩形ABCD与矩形A′B′C′D′相似.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
