2021-2022学年人教版九年级数学上册第23章旋转期末复习训练(word解析版)
文档属性
| 名称 | 2021-2022学年人教版九年级数学上册第23章旋转期末复习训练(word解析版) |  | |
| 格式 | doc | ||
| 文件大小 | 360.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-26 14:27:00 | ||
图片预览



文档简介
2021-2022学年人教版九年级数学上册《第23章旋转》期末综合复习训练(附答案)
1.在下面的网格图中,每个小正方形的边长均为1,△ABC的三个顶点都是网格线的交点,已知B,C两点的坐标分别为(﹣1,﹣1),(1,﹣2),将△ABC绕点C顺时针旋转90°,则点A的对应点的坐标为( )
A.(4,1) B.(4,﹣1) C.(5,1) D.(5,﹣1)
2.如图,将Rt△ABC(∠B=25°)绕点A顺时针方向旋转到△AB1C1的位置,使得点C,A,B1在同一条直线上,那么旋转角等于( )
A.65° B.80° C.105° D.115°
3.若两个图形关于某一点成中心对称,那么下列说法.正确的是( )
①对称点的连线必过对称中心;
②这两个图形一定全等;
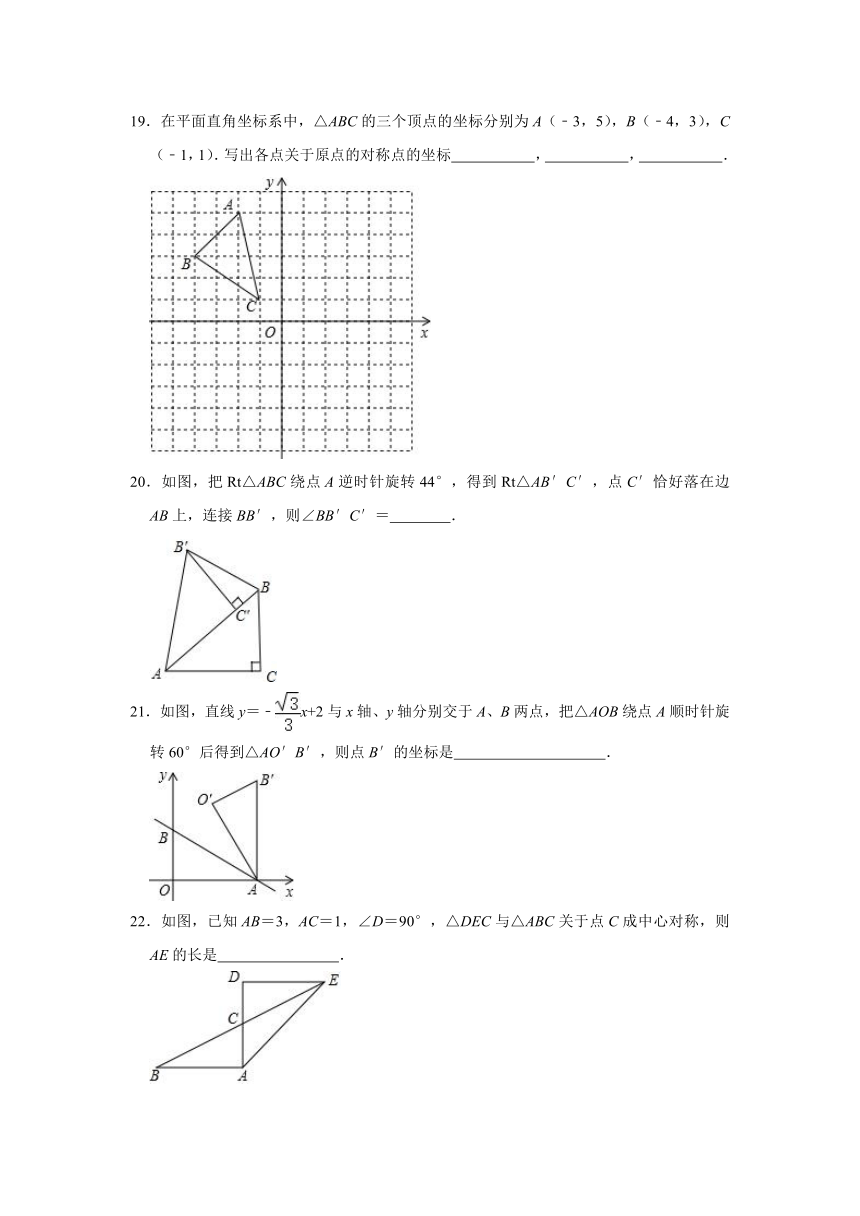
③对应线段一定平行(或在一条直线上)且相等;
④将一个图形绕对称中心旋转180°必定与另一个图形重合.
A.①② B.①③ C.①②③ D.①②③④
4.如图,平面直角坐标系内Rt△ABO的顶点A坐标为(3,1),将△ABO绕O点逆时针旋转90°后,顶点A的坐标为( )
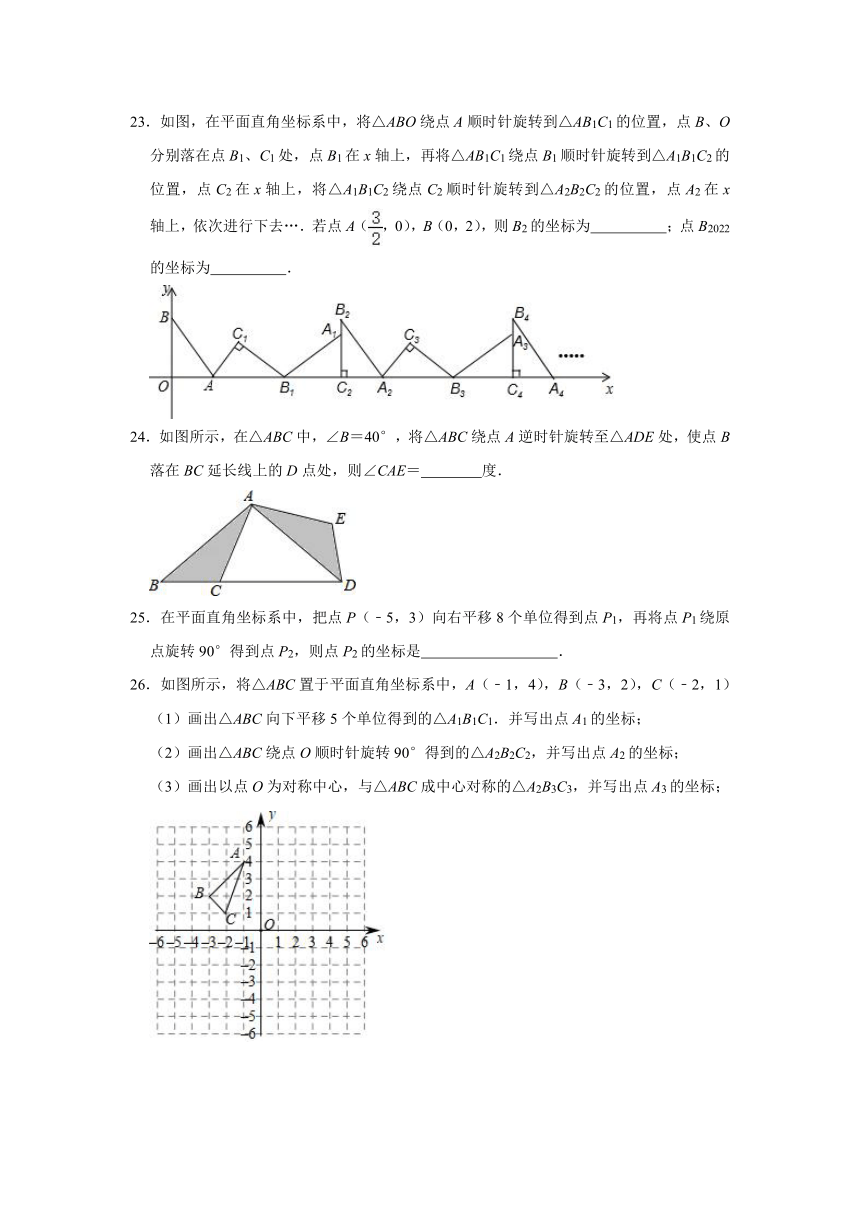
A.(﹣1,3) B.(1,﹣3) C.(3,1) D.(﹣3,1)
5.将点P(﹣2,3)向上平移3个单位得到点P1,点P2与点P1关于原点对称,则P2的坐标是( )
A.(2,6) B.(2,﹣6) C.(2,﹣3) D.(2,0)
6.下面所列图形中是中心对称图形的为( )
A. B. C. D.
7.已知点A(a,2023)与点A′(﹣2024,b)是关于原点O的对称点,则a+b的值为( )
A.1 B.5 C.6 D.4
8.在平面直角坐标系中,若点P(m,m﹣n)与点Q(﹣2,3)关于原点对称,则点M(m,n)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
9.如图,将△OAB绕点O逆时针旋转80°,得到△OCD,若∠A=2∠D=100°,则∠α的度数是( )
A.50° B.60° C.40° D.30°
10.在平面直角坐标系xOy中,A点坐标为(3,4),将OA绕原点O顺时针旋转180°得到OA′,则点A′的坐标是( )
A.(﹣4,3) B.(﹣3,﹣4) C.(﹣4,﹣3) D.(﹣3,4)
11.如图,在△ABC中,∠ACB=90°,将△ABC绕点A顺时针旋转90°,得到△ADE,连接BD,若AC=3,DE=1,则线段BD的长为( )
A.2 B.2 C.4 D.2
12.已知点M(1﹣2m,m﹣1)关于原点的对称点在第一象限,则m的取值范围在数轴上表示正确的是( )
A. B.
C. D.
13.在直角坐标系中,将点A(0,2)绕原点O逆时针方向旋转60°后的对应点B的坐标是( )
A.() B.() C.() D.()
14.如图,将△ABC绕点A逆时针旋转110°,得到△ADE,若点D在线段BC的延长线上,则∠ADE的大小为( )
A.55° B.50° C.45° D.35°
15.如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,连接AA′,若∠AA′B′=20°,则∠BAA′的度数是( )
A.70° B.65° C.60° D.55°
16.下列是中心对称图形的有( )
(1)线段;(2)角;(3)等边三角形;(4)正方形;(5)平行四边形;(6)矩形;(7)等腰梯形.
A.2个 B.3个 C.4个 D.5个
17.下列图形:直角三角形、菱形、平行四边形、等腰梯形中,是轴对称图形,但不是中心对称图形的是 .
18.如图,将△ABC绕点A按顺时针方向旋转某个角度得到△AB′C′,使AB′∥CB,CB,AC′的延长线相交于点D,如果∠D=28°,那么∠BAC= °.
19.在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(﹣3,5),B(﹣4,3),C(﹣1,1).写出各点关于原点的对称点的坐标 , , .
20.如图,把Rt△ABC绕点A逆时针旋转44°,得到Rt△AB′C′,点C′恰好落在边AB上,连接BB′,则∠BB′C′= .
21.如图,直线y=﹣x+2与x轴、y轴分别交于A、B两点,把△AOB绕点A顺时针旋转60°后得到△AO′B′,则点B′的坐标是 .
22.如图,已知AB=3,AC=1,∠D=90°,△DEC与△ABC关于点C成中心对称,则AE的长是 .
23.如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去….若点A(,0),B(0,2),则B2的坐标为 ;点B2022的坐标为 .
24.如图所示,在△ABC中,∠B=40°,将△ABC绕点A逆时针旋转至△ADE处,使点B落在BC延长线上的D点处,则∠CAE= 度.
25.在平面直角坐标系中,把点P(﹣5,3)向右平移8个单位得到点P1,再将点P1绕原点旋转90°得到点P2,则点P2的坐标是 .
26.如图所示,将△ABC置于平面直角坐标系中,A(﹣1,4),B(﹣3,2),C(﹣2,1)
(1)画出△ABC向下平移5个单位得到的△A1B1C1.并写出点A1的坐标;
(2)画出△ABC绕点O顺时针旋转90°得到的△A2B2C2,并写出点A2的坐标;
(3)画出以点O为对称中心,与△ABC成中心对称的△A2B3C3,并写出点A3的坐标;
27.如图,在平面直角坐标系中,已知点B(4,2),BA⊥x轴,垂足为A.
(1)将点B绕原点逆时针方向旋转90°后记作点C,求点C的坐标;
(2)△O′A′B′与△OAB关于原点对称,写出点B′、A′的坐标.
28.如图,在平面直角坐标系中,已知点A(﹣2,3),B(﹣3,1),C(﹣1,2).且△A1B1C1与△ABC关于原点O成中心对称.
(1)画出△A1B1C1,并写出A1的坐标;
(2)P(a,b)是△ABC的边AC上一点,△ABC经平移后点P的对应点P′(a+3,b+1),请画出平移后的△A2B2C2.
29.方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点B的坐标为(1,0).
(1)画出△ABC关于x轴对称的△A1B1C1;
(2)画出将△ABC绕原点O逆时针方向旋转90°所得的△A2B2C2.
30.如图,△ABC和△DEF关于点O成中心对称.
(1)作出它们的对称中心O,并简要说明作法;
(2)若AB=6,AC=5,BC=4,求△DEF的周长;
(3)连接AF,CD,试判断四边形ACDF的形状,并说明理由.
31.如图,△ABC中,AB=AC=1,∠BAC=45°,△AEF是由△ABC绕点A按顺时针方向旋转得到的,连接BE、CF相交于点D.
(1)求证:BE=CF;
(2)当四边形ACDE为菱形时,求BD的长.
32.如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4)
(1)请画出将△ABC向左平移4个单位长度后得到的图形△A1B1C1;
(2)请画出△ABC关于原点O成中心对称的图形△A2B2C2;
(3)在x轴上找一点P,使PA+PB的值最小,请直接写出点P的坐标.
33.如图,BD是△ABC的角平分线,AE⊥BD交BD的延长线于点E,∠ABC=72°,∠C:∠ADB=2:3,求∠BAC和∠DAE的度数.
34.如图,在△ABC中,∠C=80°,点D在边BC上,且∠ADB=100°,∠BAD=∠DAC,BE平分∠ABC,交AD于点E.求∠BED的大小.
参考答案
1.解:如图,A点坐标为(0,2),
将△ABC绕点C顺时针旋转90°,则点A的对应点的A′的坐标为(5,﹣1).
故选:D.
2.解:∵C,A,B1在同一条直线上,∠C=90°,∠B=25°,
∴∠BAB1=∠C+∠B=115°.故选:D.
3.解:根据分析可得:①对称点的连线必过对称中心,正确;
②中心对称的两个图形一定全等,正确;
③对应线段一定平行(或在一条直线上)且相等,正确;
④根据定义可得此说法正确;
①②③④均符合题意.
故选:D.
4.解:将△ABO绕O点逆时针旋转90°后,位置如图所示.
∵A(3,1),∴OB=3,AB=1.
∴OB′=3,A′B′=1.
∵A′在第二象限,
∴A′(﹣1,3).
故选:A.
5.解:∵点P(﹣2,3)向上平移3个单位得到点P1,
∴P1(﹣2,6),
∵点P2与点P1关于原点对称,
∴P2的坐标是:(2,﹣6).
故选:B.
6.解:A、是轴对称图形;
B、有五个角,但有旋转,所以既不是轴对称图形也不是中心对称图形;
C、即是轴对称图形,又是中心对称图形;
D、是轴对称图形.
故选:C.
7.解:∵点A(a,2023)与点A′(﹣2024,b)是关于原点O的对称点,
∴a=2024,b=﹣2023,
则a+b的值为:2024﹣2023=1.
故选:A.
8.解:根据平面内两点关于原点对称的点,横坐标与纵坐标都互为相反数,
∴m=2且m﹣n=﹣3,
∴m=2,n=5
∴点M(m,n)在第一象限,
故选:A.
9.解:∵将△OAB绕点O逆时针旋转80°
∴∠A=∠C,∠AOC=80°
∴∠DOC=80°﹣α
∵∠A=2∠D=100°
∴∠D=50°
∵∠C+∠D+∠DOC=180°
∴100°+50°+80°﹣α=180° 解得α=50°
故选:A.
10.解:根据题意得,点A关于原点的对称点是点A′,
∵A点坐标为(3,4),
∴点A′的坐标(﹣3,﹣4).
故选:B.
11.解:由旋转的性质可知:BC=DE=1,AB=AD
∵在Rt△ABC中,AC=3,BC=1,∠ACB=90°,
∴由勾股定理得:AB=AD==
又旋转角为90°,
∴∠BAD=90°,
∴在Rt△ADB中,BD==2
即:BD的长为2
故选:A.
12.解:∵点M(1﹣2m,m﹣1)关于原点的对称点在第一象限,
∴点M(1﹣2m,m﹣1)在第三象限,
∴,
解不等式①得,m>,
解不等式②得,m<1,
所以,m的取值范围是<m<1,
在数轴上表示如下:.
故选:C.
13.解:将点A(0,2)绕原点O逆时针方向旋转60°后的对应点B的坐标是(﹣,1),
故选:B.
14.解:如图,
∵将△ABC绕点A逆时针旋转110°,得到△ADE,
∴AB=AD,∠BAD=110°,∠ADE=∠ABC,
∴∠ABC=∠ADE=35°,
故选:D.
15.解:∵将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C连接AA′
∴AC=CA',∠BAC=∠CA'B',
∴∠CAA'=∠CA'A=45°,且∠AA′B′=20°,
∴∠CA'B'=25°=∠BAC,
∴∠BAA'=∠BAC+∠CAA'=70°
故选:A.
16.解:由中心对称图形的概念可知,(1)(4)(5)(6)是中心对称图形,符合题意;
(2)(3)(7)不是中心对称图形,是轴对称图形,不符合题意.
故中心对称的图形有4个.
故选:C.
17.解:直角三角形不是轴对称图形,也不是中心对称图形;
菱形是轴对称图形,也是中心对称图形;
平行四边形不是轴对称图形,是中心对称图形;
等腰梯形是轴对称图形,不是中心对称图形,
故答案为:等腰梯形.
18.解:∵AB′∥CB,
∴∠B′AC=∠D=28°,
∵△ABC绕点A按顺时针方向旋转某个角度得到△AB′C′,
∴∠BAC=∠B′AC=28°.
故答案为28.
19.解:∵两个点关于原点对称时,它们的坐标符号相反,
∴A(﹣3,5)关于原点对称的点的坐标为:(3,﹣5);
B(﹣4,3)关于原点对称的点的坐标为(4,﹣3),
C(﹣1,1)关于原点对称的点的坐标为(1,﹣1).
故答案为:(3,﹣5)、(4,﹣3)、(1,﹣1).
20.解:∵Rt△ABC绕点A逆时针旋转40°得到Rt△AB′C′,
∴AB=AB′,∠BAB′=44°,
在△ABB′中,∠ABB′=(180°﹣∠BAB′)=(180°﹣44°)=68°,
∵∠AC′B′=∠C=90°,
∴B′C′⊥AB,
∴∠BB′C′=90°﹣∠ABB′=90°﹣68°=22°.故答案为:22°.
21.解:令y=0,则﹣x+2=0,
解得x=2,
令x=0,则y=2,
∴点A(2,0),B(0,2),
∴OA=2,OB=2,
∴∠BAO=30°,
∴AB=2OB=2×2=4,
∵△AOB绕点A顺时针旋转60°后得到△AO′B′,
∴∠BAB′=60°,
∴∠OAB′=30°+60°=90°,
∴AB′⊥x轴,
∴点B′(2,4).
故答案为:(2,4).
22.解:∵△DEC 与△ABC关于点C成中心对称,
∴DC=AC=1,DE=AB=3,
∴在Rt△EDA中,AE的长是:=.故答案为:.
23.解:∵A(,0),B(0,2),
∴Rt△AOB中,AB=,
∴OA+AB1+B1C2=+2+=6,
∴B2的横坐标为:6,且B2C2=2,即B2(6,2),
∴B4的横坐标为:2×6=12,
∴点B2022的横坐标为:2022÷2×6=6066,点B2022的纵坐标为:2,
即B2022的坐标是(6066,2).
故答案为:(6,2),(6066,2).
24.解:∵△ABC绕点A逆时针旋转至△ADE处,使点B落在BC延长线上的D点处,
∴AB=AD,∠BAD等于旋转角,
∴∠B=∠ADB=40°,
∴∠BAD=180°﹣∠B﹣∠ADB=100°.
故答案为100.
25.解:∵把点P(﹣5,3)向右平移8个单位得到点P1,
∴点P1的坐标为:(3,3),
如图所示:将点P1绕原点逆时针旋转90°得到点P2,则其坐标为:(﹣3,3),
将点P1绕原点顺时针旋转90°得到点P3,则其坐标为:(3,﹣3),
故符合题意的点P的坐标为:(3,﹣3)或(﹣3,3).
故答案为:(3,﹣3)或(﹣3,3).
26.解:(1)如图,△A1B1C1为所作,点A1的坐标为(﹣1,﹣1);
(2)如图,△A2B2C2为所作,点A2的坐标为(4,1);
(3)如图,△A2B3C3为所作,点A3的坐标为(1,﹣4).
27.解:(1)如图,点C的坐标为(﹣2,4);
(2)点B′、A′的坐标分别为(﹣4,﹣2)、(﹣4,0).
28.解:(1)如图所示,△A1B1C1即为所求,A1的坐标为(2,﹣3);
(2)如图所示,△A2B2C2即为所求.
29.解:(1)如图所示:△A1B1C1,即为所求;
(2)如图所示:△A2B2C2,即为所求.
30.解:(1)如图所示,点O即为所求;
(2)∵△ABC和△DEF关于点O成中心对称,
∴△ABC≌△DEF,
∴AB=DE=6,AC=DF=5,BC=EF=4,
∴△DEF的周长为15;
(3)∵△ABC和△DEF关于点O成中心对称,
∴OA=OD,OC=OF,
∴四边形ACDF是平行四边形.
31.(1)证明:∵△AEF是由△ABC绕点A按顺时针方向旋转得到的,
∴AE=AB,AF=AC,∠EAF=∠BAC,
∴∠EAF+∠BAF=∠BAC+∠BAF,即∠EAB=∠FAC,
∵AB=AC,
∴AE=AF,
∴△AEB可由△AFC绕点A按顺时针方向旋转得到,
∴BE=CF;
(2)解:∵四边形ACDE为菱形,AB=AC=1,
∴DE=AE=AC=AB=1,AC∥DE,
∴∠AEB=∠ABE,∠ABE=∠BAC=45°,
∴∠AEB=∠ABE=45°,
∴△ABE为等腰直角三角形,
∴BE=AC=,
∴BD=BE﹣DE=﹣1.
32.解:(1)如图1所示:
(2)如图2所示:
(3)找出A的对称点A′(1,﹣1),
连接BA′,与x轴交点即为P;
如图3所示:点P坐标为(2,0).
33.解:设∠C=2x,则∠ADB=3x,
∵BD平分∠ABC,∠ABC=72°,
∴∠ABD=∠CBD=36°,
∵∠ADB=∠DBC+∠C,
∴3x=36°+2x,
∴x=36°,
∴∠C=72°,∠ADB=108°,
∴∠BAC=180°﹣72°﹣72°=36°,
∵AE⊥BE,
∴∠E=90°,
∵∠ADB=∠E+∠DAE,
∴∠DAE=108°﹣90°=18°.
34.解:∵∠ADB=∠C+∠DAC,∠ADB=100°,∠C=80°,
∴∠DAC=∠ADB﹣∠C=100°﹣80°=20°,
∵,
∴20°=10°,
在△ABD中,∠ABC=180°﹣∠ADB﹣∠BAD=180°﹣100°﹣10°=70°,
∵BE平分∠ABC,
∴70°=35°,
∴∠BED=∠BAD+∠ABE=10°+35°=45°.
1.在下面的网格图中,每个小正方形的边长均为1,△ABC的三个顶点都是网格线的交点,已知B,C两点的坐标分别为(﹣1,﹣1),(1,﹣2),将△ABC绕点C顺时针旋转90°,则点A的对应点的坐标为( )
A.(4,1) B.(4,﹣1) C.(5,1) D.(5,﹣1)
2.如图,将Rt△ABC(∠B=25°)绕点A顺时针方向旋转到△AB1C1的位置,使得点C,A,B1在同一条直线上,那么旋转角等于( )
A.65° B.80° C.105° D.115°
3.若两个图形关于某一点成中心对称,那么下列说法.正确的是( )
①对称点的连线必过对称中心;
②这两个图形一定全等;
③对应线段一定平行(或在一条直线上)且相等;
④将一个图形绕对称中心旋转180°必定与另一个图形重合.
A.①② B.①③ C.①②③ D.①②③④
4.如图,平面直角坐标系内Rt△ABO的顶点A坐标为(3,1),将△ABO绕O点逆时针旋转90°后,顶点A的坐标为( )
A.(﹣1,3) B.(1,﹣3) C.(3,1) D.(﹣3,1)
5.将点P(﹣2,3)向上平移3个单位得到点P1,点P2与点P1关于原点对称,则P2的坐标是( )
A.(2,6) B.(2,﹣6) C.(2,﹣3) D.(2,0)
6.下面所列图形中是中心对称图形的为( )
A. B. C. D.
7.已知点A(a,2023)与点A′(﹣2024,b)是关于原点O的对称点,则a+b的值为( )
A.1 B.5 C.6 D.4
8.在平面直角坐标系中,若点P(m,m﹣n)与点Q(﹣2,3)关于原点对称,则点M(m,n)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
9.如图,将△OAB绕点O逆时针旋转80°,得到△OCD,若∠A=2∠D=100°,则∠α的度数是( )
A.50° B.60° C.40° D.30°
10.在平面直角坐标系xOy中,A点坐标为(3,4),将OA绕原点O顺时针旋转180°得到OA′,则点A′的坐标是( )
A.(﹣4,3) B.(﹣3,﹣4) C.(﹣4,﹣3) D.(﹣3,4)
11.如图,在△ABC中,∠ACB=90°,将△ABC绕点A顺时针旋转90°,得到△ADE,连接BD,若AC=3,DE=1,则线段BD的长为( )
A.2 B.2 C.4 D.2
12.已知点M(1﹣2m,m﹣1)关于原点的对称点在第一象限,则m的取值范围在数轴上表示正确的是( )
A. B.
C. D.
13.在直角坐标系中,将点A(0,2)绕原点O逆时针方向旋转60°后的对应点B的坐标是( )
A.() B.() C.() D.()
14.如图,将△ABC绕点A逆时针旋转110°,得到△ADE,若点D在线段BC的延长线上,则∠ADE的大小为( )
A.55° B.50° C.45° D.35°
15.如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,连接AA′,若∠AA′B′=20°,则∠BAA′的度数是( )
A.70° B.65° C.60° D.55°
16.下列是中心对称图形的有( )
(1)线段;(2)角;(3)等边三角形;(4)正方形;(5)平行四边形;(6)矩形;(7)等腰梯形.
A.2个 B.3个 C.4个 D.5个
17.下列图形:直角三角形、菱形、平行四边形、等腰梯形中,是轴对称图形,但不是中心对称图形的是 .
18.如图,将△ABC绕点A按顺时针方向旋转某个角度得到△AB′C′,使AB′∥CB,CB,AC′的延长线相交于点D,如果∠D=28°,那么∠BAC= °.
19.在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(﹣3,5),B(﹣4,3),C(﹣1,1).写出各点关于原点的对称点的坐标 , , .
20.如图,把Rt△ABC绕点A逆时针旋转44°,得到Rt△AB′C′,点C′恰好落在边AB上,连接BB′,则∠BB′C′= .
21.如图,直线y=﹣x+2与x轴、y轴分别交于A、B两点,把△AOB绕点A顺时针旋转60°后得到△AO′B′,则点B′的坐标是 .
22.如图,已知AB=3,AC=1,∠D=90°,△DEC与△ABC关于点C成中心对称,则AE的长是 .
23.如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去….若点A(,0),B(0,2),则B2的坐标为 ;点B2022的坐标为 .
24.如图所示,在△ABC中,∠B=40°,将△ABC绕点A逆时针旋转至△ADE处,使点B落在BC延长线上的D点处,则∠CAE= 度.
25.在平面直角坐标系中,把点P(﹣5,3)向右平移8个单位得到点P1,再将点P1绕原点旋转90°得到点P2,则点P2的坐标是 .
26.如图所示,将△ABC置于平面直角坐标系中,A(﹣1,4),B(﹣3,2),C(﹣2,1)
(1)画出△ABC向下平移5个单位得到的△A1B1C1.并写出点A1的坐标;
(2)画出△ABC绕点O顺时针旋转90°得到的△A2B2C2,并写出点A2的坐标;
(3)画出以点O为对称中心,与△ABC成中心对称的△A2B3C3,并写出点A3的坐标;
27.如图,在平面直角坐标系中,已知点B(4,2),BA⊥x轴,垂足为A.
(1)将点B绕原点逆时针方向旋转90°后记作点C,求点C的坐标;
(2)△O′A′B′与△OAB关于原点对称,写出点B′、A′的坐标.
28.如图,在平面直角坐标系中,已知点A(﹣2,3),B(﹣3,1),C(﹣1,2).且△A1B1C1与△ABC关于原点O成中心对称.
(1)画出△A1B1C1,并写出A1的坐标;
(2)P(a,b)是△ABC的边AC上一点,△ABC经平移后点P的对应点P′(a+3,b+1),请画出平移后的△A2B2C2.
29.方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点B的坐标为(1,0).
(1)画出△ABC关于x轴对称的△A1B1C1;
(2)画出将△ABC绕原点O逆时针方向旋转90°所得的△A2B2C2.
30.如图,△ABC和△DEF关于点O成中心对称.
(1)作出它们的对称中心O,并简要说明作法;
(2)若AB=6,AC=5,BC=4,求△DEF的周长;
(3)连接AF,CD,试判断四边形ACDF的形状,并说明理由.
31.如图,△ABC中,AB=AC=1,∠BAC=45°,△AEF是由△ABC绕点A按顺时针方向旋转得到的,连接BE、CF相交于点D.
(1)求证:BE=CF;
(2)当四边形ACDE为菱形时,求BD的长.
32.如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4)
(1)请画出将△ABC向左平移4个单位长度后得到的图形△A1B1C1;
(2)请画出△ABC关于原点O成中心对称的图形△A2B2C2;
(3)在x轴上找一点P,使PA+PB的值最小,请直接写出点P的坐标.
33.如图,BD是△ABC的角平分线,AE⊥BD交BD的延长线于点E,∠ABC=72°,∠C:∠ADB=2:3,求∠BAC和∠DAE的度数.
34.如图,在△ABC中,∠C=80°,点D在边BC上,且∠ADB=100°,∠BAD=∠DAC,BE平分∠ABC,交AD于点E.求∠BED的大小.
参考答案
1.解:如图,A点坐标为(0,2),
将△ABC绕点C顺时针旋转90°,则点A的对应点的A′的坐标为(5,﹣1).
故选:D.
2.解:∵C,A,B1在同一条直线上,∠C=90°,∠B=25°,
∴∠BAB1=∠C+∠B=115°.故选:D.
3.解:根据分析可得:①对称点的连线必过对称中心,正确;
②中心对称的两个图形一定全等,正确;
③对应线段一定平行(或在一条直线上)且相等,正确;
④根据定义可得此说法正确;
①②③④均符合题意.
故选:D.
4.解:将△ABO绕O点逆时针旋转90°后,位置如图所示.
∵A(3,1),∴OB=3,AB=1.
∴OB′=3,A′B′=1.
∵A′在第二象限,
∴A′(﹣1,3).
故选:A.
5.解:∵点P(﹣2,3)向上平移3个单位得到点P1,
∴P1(﹣2,6),
∵点P2与点P1关于原点对称,
∴P2的坐标是:(2,﹣6).
故选:B.
6.解:A、是轴对称图形;
B、有五个角,但有旋转,所以既不是轴对称图形也不是中心对称图形;
C、即是轴对称图形,又是中心对称图形;
D、是轴对称图形.
故选:C.
7.解:∵点A(a,2023)与点A′(﹣2024,b)是关于原点O的对称点,
∴a=2024,b=﹣2023,
则a+b的值为:2024﹣2023=1.
故选:A.
8.解:根据平面内两点关于原点对称的点,横坐标与纵坐标都互为相反数,
∴m=2且m﹣n=﹣3,
∴m=2,n=5
∴点M(m,n)在第一象限,
故选:A.
9.解:∵将△OAB绕点O逆时针旋转80°
∴∠A=∠C,∠AOC=80°
∴∠DOC=80°﹣α
∵∠A=2∠D=100°
∴∠D=50°
∵∠C+∠D+∠DOC=180°
∴100°+50°+80°﹣α=180° 解得α=50°
故选:A.
10.解:根据题意得,点A关于原点的对称点是点A′,
∵A点坐标为(3,4),
∴点A′的坐标(﹣3,﹣4).
故选:B.
11.解:由旋转的性质可知:BC=DE=1,AB=AD
∵在Rt△ABC中,AC=3,BC=1,∠ACB=90°,
∴由勾股定理得:AB=AD==
又旋转角为90°,
∴∠BAD=90°,
∴在Rt△ADB中,BD==2
即:BD的长为2
故选:A.
12.解:∵点M(1﹣2m,m﹣1)关于原点的对称点在第一象限,
∴点M(1﹣2m,m﹣1)在第三象限,
∴,
解不等式①得,m>,
解不等式②得,m<1,
所以,m的取值范围是<m<1,
在数轴上表示如下:.
故选:C.
13.解:将点A(0,2)绕原点O逆时针方向旋转60°后的对应点B的坐标是(﹣,1),
故选:B.
14.解:如图,
∵将△ABC绕点A逆时针旋转110°,得到△ADE,
∴AB=AD,∠BAD=110°,∠ADE=∠ABC,
∴∠ABC=∠ADE=35°,
故选:D.
15.解:∵将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C连接AA′
∴AC=CA',∠BAC=∠CA'B',
∴∠CAA'=∠CA'A=45°,且∠AA′B′=20°,
∴∠CA'B'=25°=∠BAC,
∴∠BAA'=∠BAC+∠CAA'=70°
故选:A.
16.解:由中心对称图形的概念可知,(1)(4)(5)(6)是中心对称图形,符合题意;
(2)(3)(7)不是中心对称图形,是轴对称图形,不符合题意.
故中心对称的图形有4个.
故选:C.
17.解:直角三角形不是轴对称图形,也不是中心对称图形;
菱形是轴对称图形,也是中心对称图形;
平行四边形不是轴对称图形,是中心对称图形;
等腰梯形是轴对称图形,不是中心对称图形,
故答案为:等腰梯形.
18.解:∵AB′∥CB,
∴∠B′AC=∠D=28°,
∵△ABC绕点A按顺时针方向旋转某个角度得到△AB′C′,
∴∠BAC=∠B′AC=28°.
故答案为28.
19.解:∵两个点关于原点对称时,它们的坐标符号相反,
∴A(﹣3,5)关于原点对称的点的坐标为:(3,﹣5);
B(﹣4,3)关于原点对称的点的坐标为(4,﹣3),
C(﹣1,1)关于原点对称的点的坐标为(1,﹣1).
故答案为:(3,﹣5)、(4,﹣3)、(1,﹣1).
20.解:∵Rt△ABC绕点A逆时针旋转40°得到Rt△AB′C′,
∴AB=AB′,∠BAB′=44°,
在△ABB′中,∠ABB′=(180°﹣∠BAB′)=(180°﹣44°)=68°,
∵∠AC′B′=∠C=90°,
∴B′C′⊥AB,
∴∠BB′C′=90°﹣∠ABB′=90°﹣68°=22°.故答案为:22°.
21.解:令y=0,则﹣x+2=0,
解得x=2,
令x=0,则y=2,
∴点A(2,0),B(0,2),
∴OA=2,OB=2,
∴∠BAO=30°,
∴AB=2OB=2×2=4,
∵△AOB绕点A顺时针旋转60°后得到△AO′B′,
∴∠BAB′=60°,
∴∠OAB′=30°+60°=90°,
∴AB′⊥x轴,
∴点B′(2,4).
故答案为:(2,4).
22.解:∵△DEC 与△ABC关于点C成中心对称,
∴DC=AC=1,DE=AB=3,
∴在Rt△EDA中,AE的长是:=.故答案为:.
23.解:∵A(,0),B(0,2),
∴Rt△AOB中,AB=,
∴OA+AB1+B1C2=+2+=6,
∴B2的横坐标为:6,且B2C2=2,即B2(6,2),
∴B4的横坐标为:2×6=12,
∴点B2022的横坐标为:2022÷2×6=6066,点B2022的纵坐标为:2,
即B2022的坐标是(6066,2).
故答案为:(6,2),(6066,2).
24.解:∵△ABC绕点A逆时针旋转至△ADE处,使点B落在BC延长线上的D点处,
∴AB=AD,∠BAD等于旋转角,
∴∠B=∠ADB=40°,
∴∠BAD=180°﹣∠B﹣∠ADB=100°.
故答案为100.
25.解:∵把点P(﹣5,3)向右平移8个单位得到点P1,
∴点P1的坐标为:(3,3),
如图所示:将点P1绕原点逆时针旋转90°得到点P2,则其坐标为:(﹣3,3),
将点P1绕原点顺时针旋转90°得到点P3,则其坐标为:(3,﹣3),
故符合题意的点P的坐标为:(3,﹣3)或(﹣3,3).
故答案为:(3,﹣3)或(﹣3,3).
26.解:(1)如图,△A1B1C1为所作,点A1的坐标为(﹣1,﹣1);
(2)如图,△A2B2C2为所作,点A2的坐标为(4,1);
(3)如图,△A2B3C3为所作,点A3的坐标为(1,﹣4).
27.解:(1)如图,点C的坐标为(﹣2,4);
(2)点B′、A′的坐标分别为(﹣4,﹣2)、(﹣4,0).
28.解:(1)如图所示,△A1B1C1即为所求,A1的坐标为(2,﹣3);
(2)如图所示,△A2B2C2即为所求.
29.解:(1)如图所示:△A1B1C1,即为所求;
(2)如图所示:△A2B2C2,即为所求.
30.解:(1)如图所示,点O即为所求;
(2)∵△ABC和△DEF关于点O成中心对称,
∴△ABC≌△DEF,
∴AB=DE=6,AC=DF=5,BC=EF=4,
∴△DEF的周长为15;
(3)∵△ABC和△DEF关于点O成中心对称,
∴OA=OD,OC=OF,
∴四边形ACDF是平行四边形.
31.(1)证明:∵△AEF是由△ABC绕点A按顺时针方向旋转得到的,
∴AE=AB,AF=AC,∠EAF=∠BAC,
∴∠EAF+∠BAF=∠BAC+∠BAF,即∠EAB=∠FAC,
∵AB=AC,
∴AE=AF,
∴△AEB可由△AFC绕点A按顺时针方向旋转得到,
∴BE=CF;
(2)解:∵四边形ACDE为菱形,AB=AC=1,
∴DE=AE=AC=AB=1,AC∥DE,
∴∠AEB=∠ABE,∠ABE=∠BAC=45°,
∴∠AEB=∠ABE=45°,
∴△ABE为等腰直角三角形,
∴BE=AC=,
∴BD=BE﹣DE=﹣1.
32.解:(1)如图1所示:
(2)如图2所示:
(3)找出A的对称点A′(1,﹣1),
连接BA′,与x轴交点即为P;
如图3所示:点P坐标为(2,0).
33.解:设∠C=2x,则∠ADB=3x,
∵BD平分∠ABC,∠ABC=72°,
∴∠ABD=∠CBD=36°,
∵∠ADB=∠DBC+∠C,
∴3x=36°+2x,
∴x=36°,
∴∠C=72°,∠ADB=108°,
∴∠BAC=180°﹣72°﹣72°=36°,
∵AE⊥BE,
∴∠E=90°,
∵∠ADB=∠E+∠DAE,
∴∠DAE=108°﹣90°=18°.
34.解:∵∠ADB=∠C+∠DAC,∠ADB=100°,∠C=80°,
∴∠DAC=∠ADB﹣∠C=100°﹣80°=20°,
∵,
∴20°=10°,
在△ABD中,∠ABC=180°﹣∠ADB﹣∠BAD=180°﹣100°﹣10°=70°,
∵BE平分∠ABC,
∴70°=35°,
∴∠BED=∠BAD+∠ABE=10°+35°=45°.
同课章节目录
