2021-2022学年北师大版八年级数学上册第3章位置与坐标 期末复习提升训练(word版含答案)
文档属性
| 名称 | 2021-2022学年北师大版八年级数学上册第3章位置与坐标 期末复习提升训练(word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 167.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-26 00:00:00 | ||
图片预览



文档简介
2021-2022学年北师大版八年级数学上册《第3章位置与坐标》
期末复习提升训练2(附答案)
1.点P(﹣3,4)到y轴的距离是( )
A.3 B.4 C.﹣3 D.5
2.平面直角坐标系中,点P的坐标为(﹣5,3),则点P关于y轴的对称点的坐标是( )
A.(5,3) B.(﹣5,﹣3) C.(3,﹣5) D.(﹣3,5)
3.平面直角坐标系中,点A在第四象限,点A到x轴的距离为2,到y轴的距离为3,则点A的坐标为( )
A.(2,﹣3) B.(﹣3,2) C.(3,﹣2) D.(﹣2,3)
4.在平面直角坐标系中,若点P(m+3,m﹣1)在x轴上,则m的值是( )
A.﹣3 B.1 C.3 D.﹣1
5.已知点A(a,2015)与点A′(﹣2016,b)是关于原点O的对称点,则a+b的值为( )
A.1 B.5 C.6 D.4
6.如图,下列各点在阴影区域内的是( )
(﹣,4) B.(3,﹣2)
C.(﹣5,5) D.(﹣2,﹣1)
7.无论m为何值,点A(m,5﹣2m)不可能在( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
8.若0<a<1,则点M(a﹣1,a)在第( )象限.
A.一 B.二 C.三 D.四
9.将点(1,﹣2)向右平移3个单位得到新的点的坐标为( )
A.(1,﹣5) B.(4,﹣2) C.(1,1) D.(﹣2,2)
10.如图,将正方形OABC放在平面直角坐标系中,O是原点,A的坐标为(1,),则点C的坐标为( )
(﹣,1) B.(﹣1,)
C.(,1) D.(﹣,﹣1)
11.一个小球从点A(3,3)出发,经过y轴上点C反弹后经过点B(1,0),则小球从A点经过点C到B点经过的最短路线长是( )
A.4 B.5 C.6 D.7
12.在电影票上,将“7排6号”表示为(7,6),那么“5排4号”应该表示为 .
13.点A(a,4)、点B(3,b)关于x轴对称,则(a+b)2010的值为 .
14.在平面直角坐标系中,点A的坐标为(﹣1,3),线段AB∥x轴,且AB=4,则点B的坐标为 .
15.已知点A(3,2),AC⊥x轴,垂足为C,则C点的坐标为 .
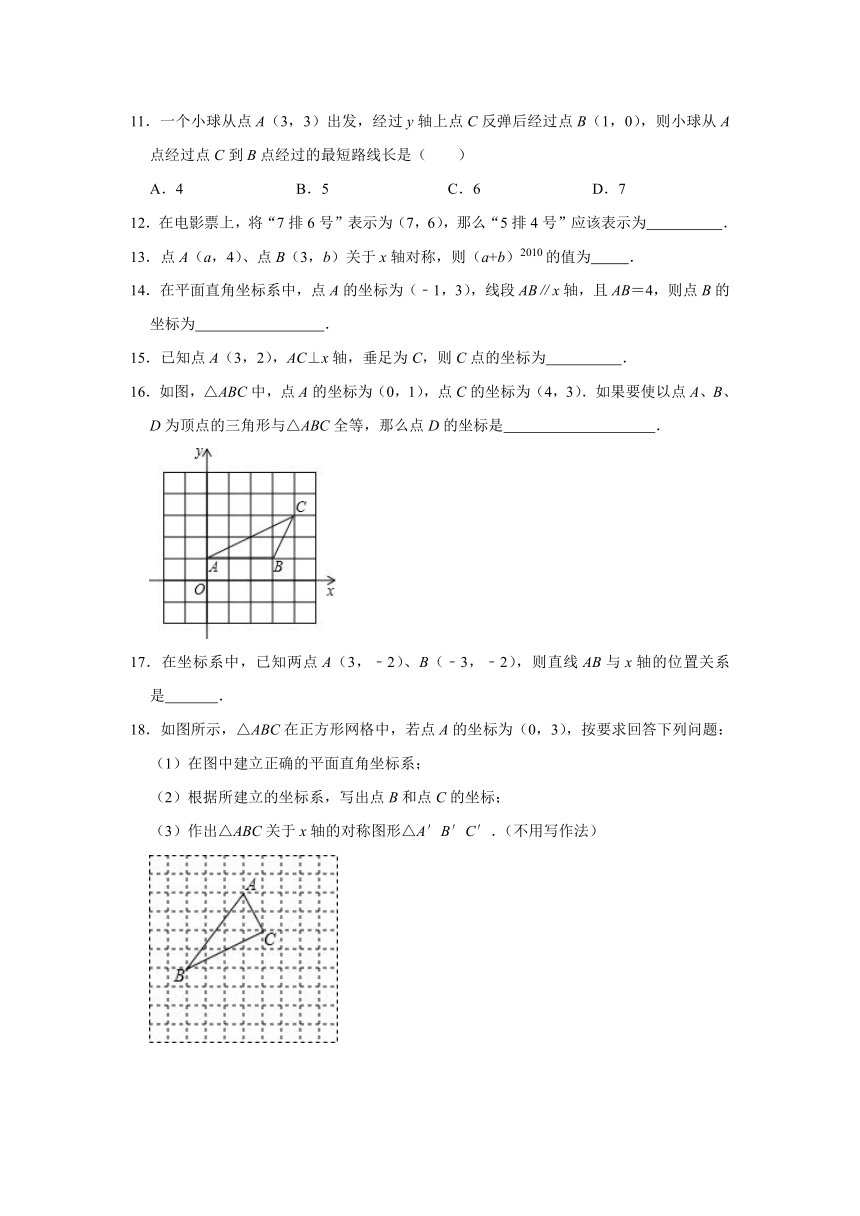
16.如图,△ABC中,点A的坐标为(0,1),点C的坐标为(4,3).如果要使以点A、B、D为顶点的三角形与△ABC全等,那么点D的坐标是 .
17.在坐标系中,已知两点A(3,﹣2)、B(﹣3,﹣2),则直线AB与x轴的位置关系是 .
18.如图所示,△ABC在正方形网格中,若点A的坐标为(0,3),按要求回答下列问题:
(1)在图中建立正确的平面直角坐标系;
(2)根据所建立的坐标系,写出点B和点C的坐标;
(3)作出△ABC关于x轴的对称图形△A′B′C′.(不用写作法)
19.如图所示,在平面直角坐标系中,点A,B的坐标分别为A(a,0),B(b,0),且a,b满足|a+2|+=0,点C的坐标为(0,3).
(1)求a,b的值及S△ABC;
(2)若点M在x轴上,且S三角形ACM=S三角形ABC,试求点M的坐标.
20.如图所示,在平面内有四个点,它们的坐标分别是A(﹣1,0),B(2+,0),C(2,1),D(0,1).
(1)依次连接A、B、C、D,围成的四边形是一个 形;
(2)求这个四边形的面积;
(3)将这个四边形向左平移个单位长度,四个顶点的坐标分别为多少?
21.对于边长为6的等边三角形ABC,建立适当的直角坐标系,写出各个顶点的坐标.
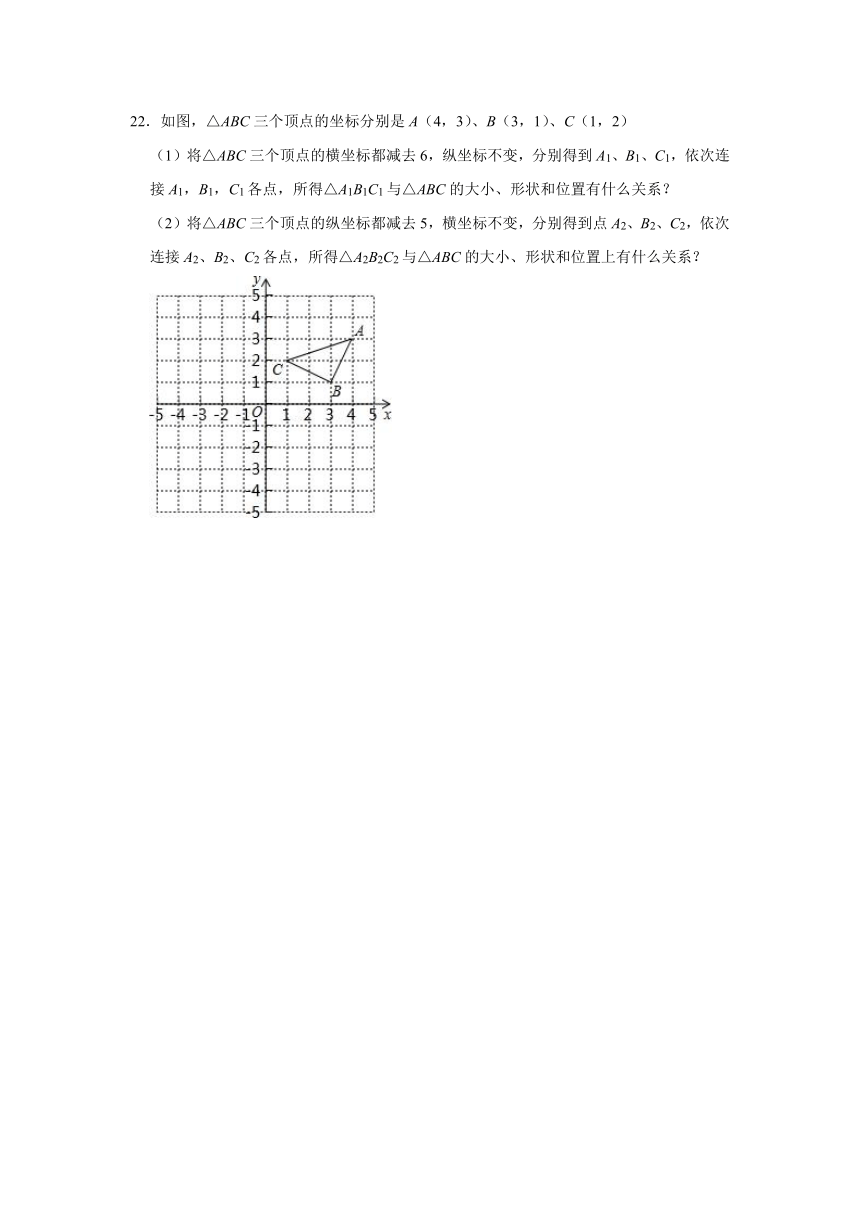
22.如图,△ABC三个顶点的坐标分别是A(4,3)、B(3,1)、C(1,2)
(1)将△ABC三个顶点的横坐标都减去6,纵坐标不变,分别得到A1、B1、C1,依次连接A1,B1,C1各点,所得△A1B1C1与△ABC的大小、形状和位置有什么关系?
(2)将△ABC三个顶点的纵坐标都减去5,横坐标不变,分别得到点A2、B2、C2,依次连接A2、B2、C2各点,所得△A2B2C2与△ABC的大小、形状和位置上有什么关系?
参考答案
1.解:点P(﹣3,4)到y轴的距离是|﹣3|=3.
故选:A.
2.解:点P(﹣5,3)关于y轴的对称点的坐标是(5,3).
故选:A.
3.解:∵点A在第四象限,点A到x轴的距离为2,到y轴的距离为3,
∴点A的横坐标是3,
纵坐标是﹣2,
∴点A的坐标为(3,﹣2).
故选:C.
4.解:∵点P(m+3,m﹣1)在x轴上,
∴m﹣1=0,
解得m=1.
故选:B.
5.解:∵点A(a,2015)与点A′(﹣2016,b)是关于原点O的对称点,
∴a=2016,b=﹣2015,
∴a+b=1,
故选:A.
6.解:A、(﹣,4)在第二象限,故本选项错误;
B、(3,﹣2)在第四象限,故本选项错误;
C、(﹣5,5)在第二象限,故本选项错误;
D、(﹣2,﹣1)在第三象限,故本选项正确.
故选:D.
7.解:当m<0时,5﹣2m>0,点A(m,5﹣2m)在第二象限,
当0<m时,点A(m,5﹣2m)在第一象限,
当m时,点A(m,5﹣2m)在第四象限.
故选:C.
8.解:∵0<a<1,
∴﹣1<a﹣1<0,
∴点M(a﹣1,a)第二象限.
故选:B.
9.解:将点P(1,﹣2)向右平移3个单位,
则点横坐标加3,纵坐标不变,即新的坐标为(4,﹣2).
故选:B.
10.解:如图,过点A作AD⊥x轴于D,过点C作CE⊥x轴于E,
∵四边形OABC是正方形,
∴OA=OC,∠AOC=90°,
∴∠COE+∠AOD=90°,
又∵∠OAD+∠AOD=90°,
∴∠OAD=∠COE,
在△AOD和△OCE中,
,
∴△AOD≌△OCE(AAS),
∴OE=AD=,CE=OD=1,
∵点C在第二象限,
∴点C的坐标为(﹣,1).
故选:A.
11.解:如果将y轴当成平面镜,设A点关于y轴的对称点为A′,则由小球路线知识可知,A′相当于A的像点,光线从A到C到B,相当于小球路线从A′直接到B,所以C点就是A′B与y轴的交点.
∵A点关于y轴的对称点为A′,A(3,3),
∴A′(﹣3,3),
进而由两点式写出A′B的直线方程为:y=﹣(x﹣1).
令x=0,求得y=.所以C点坐标为(0,).
那么根据勾股定理,可得:
AC=,BC=.
因此,AC+BC=5.
故选:B.
12.解:∵“7排6号”表示为(7,6),
∴“5排4号”应该表示为(5,4).
故答案为:(5,4).
13.解:∵点A(a,4)、点B(3,b)关于x轴对称,
∴a=3,b=﹣4,
∴(a+b)2010=1,
故答案为:1.
14.解:∵AB∥x轴,
∴A、B两点纵坐标都为3,
又∵AB=4,
∴当B点在A点左边时,B(﹣5,3),
当B点在A点右边时,B(3,3);
故答案为:(﹣5,3)或(3,3).
15.解:∵点A(3,2),AC⊥x轴,
∴直线AC的解析式为x=3,
∵点C的坐标为(3,0).
故答案为:(3,0).
16.解:符合题意的有3个,如图,
∵点A、B、C坐标为(0,1),(3,1),(4,3),
∴D1的坐标是(4,﹣1),D2的坐标是(﹣1,3),D3的坐标是(﹣1,﹣1),
故答案为:(4,﹣1)或(﹣1,3)或(﹣1,﹣1).
17.解:
∵A(3,﹣2)、B(﹣3,﹣2),
∴A、B两点到x轴的距离相等且在x轴的下方,
∴AB∥x轴,
故答案为:平行.
18.解:(1)所建立的平面直角坐标系如下所示:
(2)点B和点C的坐标分别为:B(﹣3,﹣1)C(1,1);
(3)所作△A'B'C'如下图所示.
19.解:(1)∵|a+2|+=0,
∴a+2=0,b﹣4=0,
∴a=﹣2,b=4,
∴点A(﹣2,0),点B(4,0).
又∵点C(0,3),
∴AB=|﹣2﹣4|=6,CO=3,
∴S△ABC=AB CO=×6×3=9.
(2)设点M的坐标为(x,0),则AM=|x﹣(﹣2)|=|x+2|,
又∵S△ACM=S△ABC,
∴AM OC=×9,
∴|x+2|×3=3,
∴|x+2|=2,
即x+2=±2,
解得:x=0或﹣4,
故点M的坐标为(0,0)或(﹣4,0).
20.解:(1)如图所示;
依次连接A、B、C、D,围成的四边形是一个梯形.
故答案为梯;
(2)∵A(﹣1,0),B(2+,0),C(2,1),D(0,1),
∴AB=3+,CD=2,
∴四边形ABCD的面积=(AB+CD) OD=(3++2)×1=;
(3)A′(﹣1﹣,0),B′(2,0),C′(2﹣,1),D′(﹣,1).
21.解:如图,以BC所在直线为x轴,以BC的中垂线为y轴,建立直角坐标系,则B、C点的坐标分别为(﹣3,0)、(3,0),
在Rt△ABO中,AB=6,BO=3,则AO==3,
∴A坐标为(0,3 ).
22.解:(1)所作图形如图所示:
△A1B1C1与△ABC的大小相等、形状不变,
是△ABC向左平移6个单位得到的图形;
(2)所作图形如图所示:
△A2B2C2与△ABC的大小相等、形状不变,
是△ABC向下平移5个单位得到的图形.
期末复习提升训练2(附答案)
1.点P(﹣3,4)到y轴的距离是( )
A.3 B.4 C.﹣3 D.5
2.平面直角坐标系中,点P的坐标为(﹣5,3),则点P关于y轴的对称点的坐标是( )
A.(5,3) B.(﹣5,﹣3) C.(3,﹣5) D.(﹣3,5)
3.平面直角坐标系中,点A在第四象限,点A到x轴的距离为2,到y轴的距离为3,则点A的坐标为( )
A.(2,﹣3) B.(﹣3,2) C.(3,﹣2) D.(﹣2,3)
4.在平面直角坐标系中,若点P(m+3,m﹣1)在x轴上,则m的值是( )
A.﹣3 B.1 C.3 D.﹣1
5.已知点A(a,2015)与点A′(﹣2016,b)是关于原点O的对称点,则a+b的值为( )
A.1 B.5 C.6 D.4
6.如图,下列各点在阴影区域内的是( )
(﹣,4) B.(3,﹣2)
C.(﹣5,5) D.(﹣2,﹣1)
7.无论m为何值,点A(m,5﹣2m)不可能在( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
8.若0<a<1,则点M(a﹣1,a)在第( )象限.
A.一 B.二 C.三 D.四
9.将点(1,﹣2)向右平移3个单位得到新的点的坐标为( )
A.(1,﹣5) B.(4,﹣2) C.(1,1) D.(﹣2,2)
10.如图,将正方形OABC放在平面直角坐标系中,O是原点,A的坐标为(1,),则点C的坐标为( )
(﹣,1) B.(﹣1,)
C.(,1) D.(﹣,﹣1)
11.一个小球从点A(3,3)出发,经过y轴上点C反弹后经过点B(1,0),则小球从A点经过点C到B点经过的最短路线长是( )
A.4 B.5 C.6 D.7
12.在电影票上,将“7排6号”表示为(7,6),那么“5排4号”应该表示为 .
13.点A(a,4)、点B(3,b)关于x轴对称,则(a+b)2010的值为 .
14.在平面直角坐标系中,点A的坐标为(﹣1,3),线段AB∥x轴,且AB=4,则点B的坐标为 .
15.已知点A(3,2),AC⊥x轴,垂足为C,则C点的坐标为 .
16.如图,△ABC中,点A的坐标为(0,1),点C的坐标为(4,3).如果要使以点A、B、D为顶点的三角形与△ABC全等,那么点D的坐标是 .
17.在坐标系中,已知两点A(3,﹣2)、B(﹣3,﹣2),则直线AB与x轴的位置关系是 .
18.如图所示,△ABC在正方形网格中,若点A的坐标为(0,3),按要求回答下列问题:
(1)在图中建立正确的平面直角坐标系;
(2)根据所建立的坐标系,写出点B和点C的坐标;
(3)作出△ABC关于x轴的对称图形△A′B′C′.(不用写作法)
19.如图所示,在平面直角坐标系中,点A,B的坐标分别为A(a,0),B(b,0),且a,b满足|a+2|+=0,点C的坐标为(0,3).
(1)求a,b的值及S△ABC;
(2)若点M在x轴上,且S三角形ACM=S三角形ABC,试求点M的坐标.
20.如图所示,在平面内有四个点,它们的坐标分别是A(﹣1,0),B(2+,0),C(2,1),D(0,1).
(1)依次连接A、B、C、D,围成的四边形是一个 形;
(2)求这个四边形的面积;
(3)将这个四边形向左平移个单位长度,四个顶点的坐标分别为多少?
21.对于边长为6的等边三角形ABC,建立适当的直角坐标系,写出各个顶点的坐标.
22.如图,△ABC三个顶点的坐标分别是A(4,3)、B(3,1)、C(1,2)
(1)将△ABC三个顶点的横坐标都减去6,纵坐标不变,分别得到A1、B1、C1,依次连接A1,B1,C1各点,所得△A1B1C1与△ABC的大小、形状和位置有什么关系?
(2)将△ABC三个顶点的纵坐标都减去5,横坐标不变,分别得到点A2、B2、C2,依次连接A2、B2、C2各点,所得△A2B2C2与△ABC的大小、形状和位置上有什么关系?
参考答案
1.解:点P(﹣3,4)到y轴的距离是|﹣3|=3.
故选:A.
2.解:点P(﹣5,3)关于y轴的对称点的坐标是(5,3).
故选:A.
3.解:∵点A在第四象限,点A到x轴的距离为2,到y轴的距离为3,
∴点A的横坐标是3,
纵坐标是﹣2,
∴点A的坐标为(3,﹣2).
故选:C.
4.解:∵点P(m+3,m﹣1)在x轴上,
∴m﹣1=0,
解得m=1.
故选:B.
5.解:∵点A(a,2015)与点A′(﹣2016,b)是关于原点O的对称点,
∴a=2016,b=﹣2015,
∴a+b=1,
故选:A.
6.解:A、(﹣,4)在第二象限,故本选项错误;
B、(3,﹣2)在第四象限,故本选项错误;
C、(﹣5,5)在第二象限,故本选项错误;
D、(﹣2,﹣1)在第三象限,故本选项正确.
故选:D.
7.解:当m<0时,5﹣2m>0,点A(m,5﹣2m)在第二象限,
当0<m时,点A(m,5﹣2m)在第一象限,
当m时,点A(m,5﹣2m)在第四象限.
故选:C.
8.解:∵0<a<1,
∴﹣1<a﹣1<0,
∴点M(a﹣1,a)第二象限.
故选:B.
9.解:将点P(1,﹣2)向右平移3个单位,
则点横坐标加3,纵坐标不变,即新的坐标为(4,﹣2).
故选:B.
10.解:如图,过点A作AD⊥x轴于D,过点C作CE⊥x轴于E,
∵四边形OABC是正方形,
∴OA=OC,∠AOC=90°,
∴∠COE+∠AOD=90°,
又∵∠OAD+∠AOD=90°,
∴∠OAD=∠COE,
在△AOD和△OCE中,
,
∴△AOD≌△OCE(AAS),
∴OE=AD=,CE=OD=1,
∵点C在第二象限,
∴点C的坐标为(﹣,1).
故选:A.
11.解:如果将y轴当成平面镜,设A点关于y轴的对称点为A′,则由小球路线知识可知,A′相当于A的像点,光线从A到C到B,相当于小球路线从A′直接到B,所以C点就是A′B与y轴的交点.
∵A点关于y轴的对称点为A′,A(3,3),
∴A′(﹣3,3),
进而由两点式写出A′B的直线方程为:y=﹣(x﹣1).
令x=0,求得y=.所以C点坐标为(0,).
那么根据勾股定理,可得:
AC=,BC=.
因此,AC+BC=5.
故选:B.
12.解:∵“7排6号”表示为(7,6),
∴“5排4号”应该表示为(5,4).
故答案为:(5,4).
13.解:∵点A(a,4)、点B(3,b)关于x轴对称,
∴a=3,b=﹣4,
∴(a+b)2010=1,
故答案为:1.
14.解:∵AB∥x轴,
∴A、B两点纵坐标都为3,
又∵AB=4,
∴当B点在A点左边时,B(﹣5,3),
当B点在A点右边时,B(3,3);
故答案为:(﹣5,3)或(3,3).
15.解:∵点A(3,2),AC⊥x轴,
∴直线AC的解析式为x=3,
∵点C的坐标为(3,0).
故答案为:(3,0).
16.解:符合题意的有3个,如图,
∵点A、B、C坐标为(0,1),(3,1),(4,3),
∴D1的坐标是(4,﹣1),D2的坐标是(﹣1,3),D3的坐标是(﹣1,﹣1),
故答案为:(4,﹣1)或(﹣1,3)或(﹣1,﹣1).
17.解:
∵A(3,﹣2)、B(﹣3,﹣2),
∴A、B两点到x轴的距离相等且在x轴的下方,
∴AB∥x轴,
故答案为:平行.
18.解:(1)所建立的平面直角坐标系如下所示:
(2)点B和点C的坐标分别为:B(﹣3,﹣1)C(1,1);
(3)所作△A'B'C'如下图所示.
19.解:(1)∵|a+2|+=0,
∴a+2=0,b﹣4=0,
∴a=﹣2,b=4,
∴点A(﹣2,0),点B(4,0).
又∵点C(0,3),
∴AB=|﹣2﹣4|=6,CO=3,
∴S△ABC=AB CO=×6×3=9.
(2)设点M的坐标为(x,0),则AM=|x﹣(﹣2)|=|x+2|,
又∵S△ACM=S△ABC,
∴AM OC=×9,
∴|x+2|×3=3,
∴|x+2|=2,
即x+2=±2,
解得:x=0或﹣4,
故点M的坐标为(0,0)或(﹣4,0).
20.解:(1)如图所示;
依次连接A、B、C、D,围成的四边形是一个梯形.
故答案为梯;
(2)∵A(﹣1,0),B(2+,0),C(2,1),D(0,1),
∴AB=3+,CD=2,
∴四边形ABCD的面积=(AB+CD) OD=(3++2)×1=;
(3)A′(﹣1﹣,0),B′(2,0),C′(2﹣,1),D′(﹣,1).
21.解:如图,以BC所在直线为x轴,以BC的中垂线为y轴,建立直角坐标系,则B、C点的坐标分别为(﹣3,0)、(3,0),
在Rt△ABO中,AB=6,BO=3,则AO==3,
∴A坐标为(0,3 ).
22.解:(1)所作图形如图所示:
△A1B1C1与△ABC的大小相等、形状不变,
是△ABC向左平移6个单位得到的图形;
(2)所作图形如图所示:
△A2B2C2与△ABC的大小相等、形状不变,
是△ABC向下平移5个单位得到的图形.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
