2021-2022学年人教版九年级数学上册第24章圆期末综合复习训练(word解析版)
文档属性
| 名称 | 2021-2022学年人教版九年级数学上册第24章圆期末综合复习训练(word解析版) |  | |
| 格式 | doc | ||
| 文件大小 | 308.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-26 14:37:32 | ||
图片预览



文档简介
2021-2022学年人教版九年级数学上册《第24章圆》期末综合复习训练(附答案)
1.如图所示,正六边形ABCDEF内接于圆O,则∠ADB的度数为( )
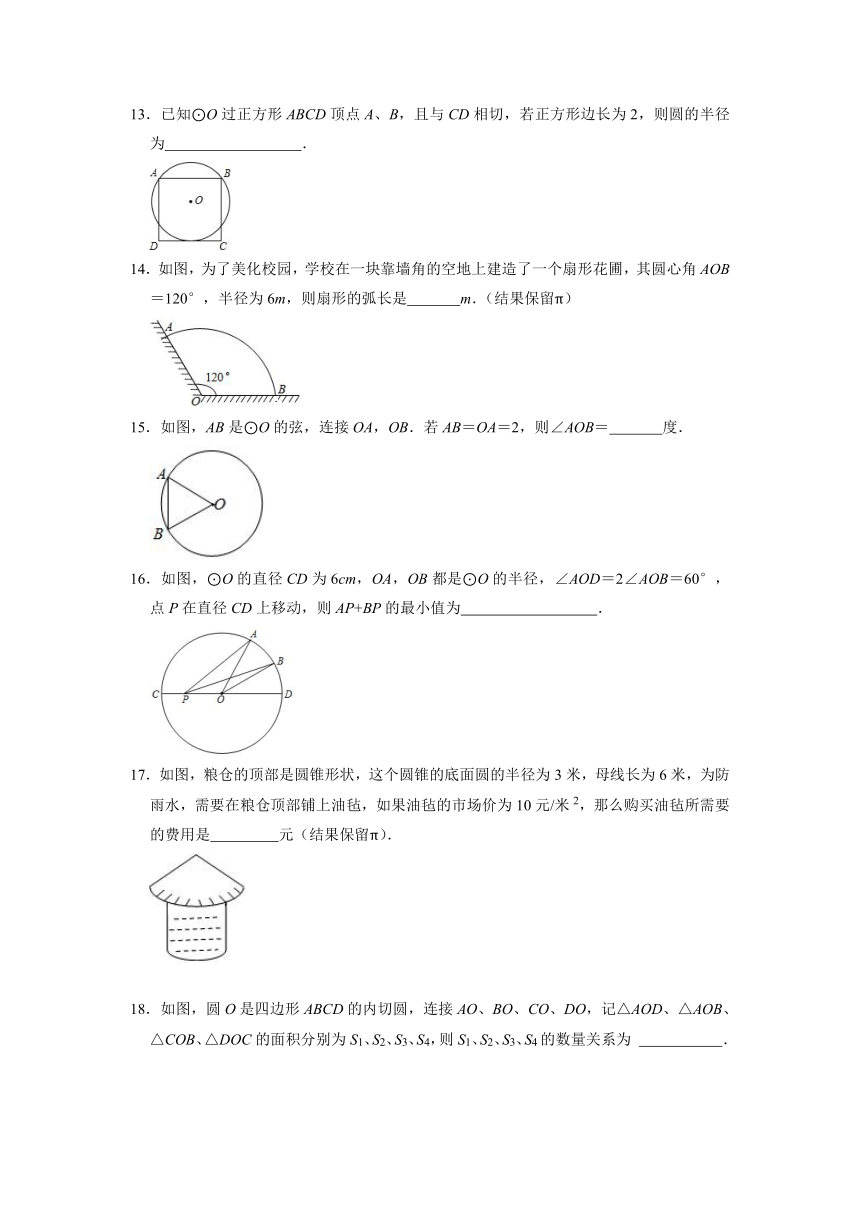
A.60° B.45° C.30° D.22.5°
2.如图,△ABC是⊙O的内接三角形,若∠ABC=60°,则∠AOC的大小是( )
A.30° B.120° C.135° D.150°
3.如图,PA、PB切⊙O于点A、B,直线FG切⊙O于点E,交PA于F,交PB于点G,若PA=8cm,则△PFG的周长是( )
A.8cm B.12cm C.16cm D.20cm
4.圆锥的截面是一个等边三角形,则它的侧面展开图圆心角度数是( )
A.60° B.90° C.120° D.180°
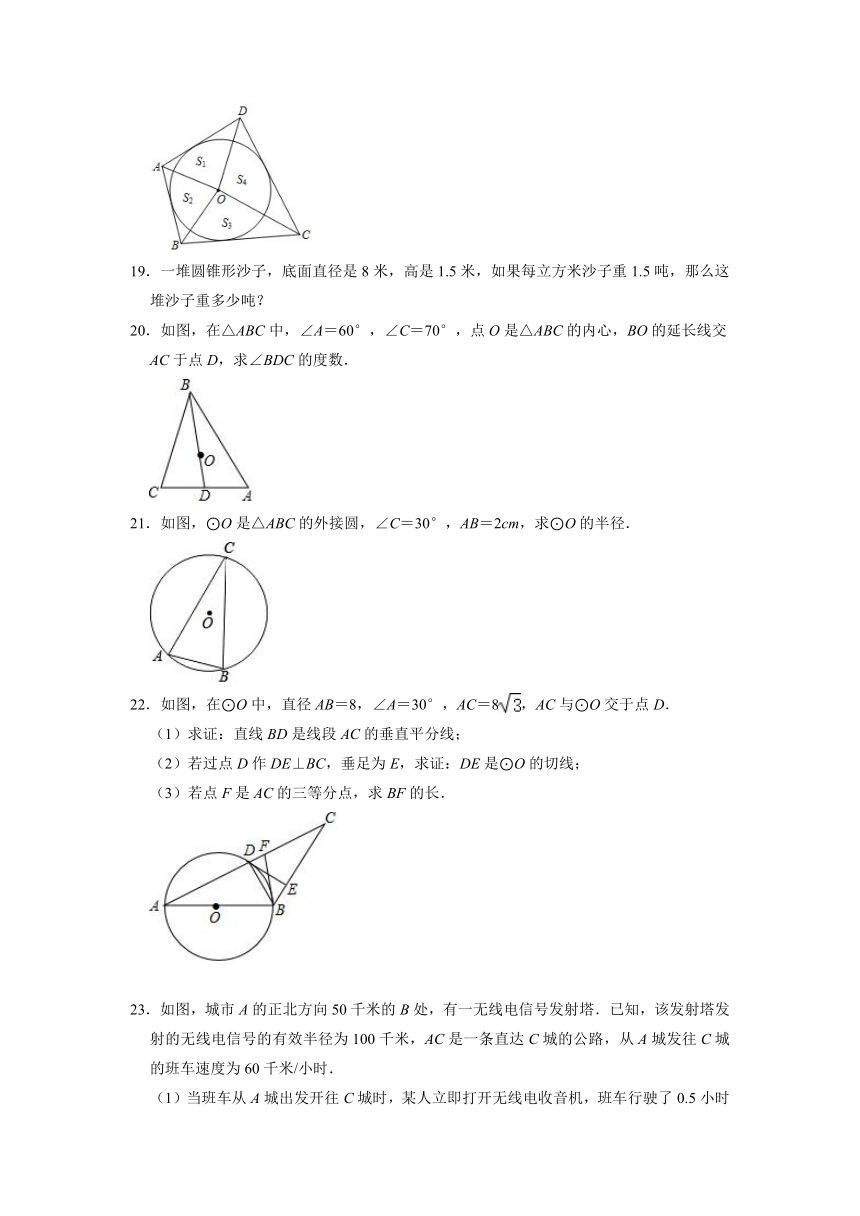
5.如图,在⊙O中,AB是直径,AC是弦,连接OC,若∠ACO=25°,则∠BOC的度数是( )
A.40° B.50° C.55° D.60°
6.如图,⊙O的半径为5,弦AB=8,点C是AB的中点,连接OC,则OC的长为( )
A.1 B.2 C.3 D.4
7.如图,A,B,C是⊙O上的三点,若∠O=70°,则∠C的度数是( )
A.40° B.35° C.30° D.25°
8.如图,四边形ABCD内接于圆O,∠BOD=108°,则∠BCD的度数是( )
A.127° B.108° C.126° D.125°
9.⊙O的半径为4cm,点P到圆心O的距离为5cm,点P与⊙O的位置关系是( )
A.点P在⊙O内 B.点P在⊙O上 C.点P在⊙O外 D.无法确定
10.如图,AB是⊙O的直径,BC是⊙O的切线,若∠BAC=35°,则∠ACB的大小为( )
A.35° B.45° C.55° D.65°
11.如图,PA是⊙O的切线,切点为A,OP=4,∠APO=30°,则⊙O的半径长为( )
A.1 B. C.2 D.3
12.已知扇形的半径为6,圆心角为150°,则它的面积是( )
A.π B.3π C.5π D.15π
13.已知⊙O过正方形ABCD顶点A、B,且与CD相切,若正方形边长为2,则圆的半径为 .
14.如图,为了美化校园,学校在一块靠墙角的空地上建造了一个扇形花圃,其圆心角AOB=120°,半径为6m,则扇形的弧长是 m.(结果保留π)
15.如图,AB是⊙O的弦,连接OA,OB.若AB=OA=2,则∠AOB= 度.
16.如图,⊙O的直径CD为6cm,OA,OB都是⊙O的半径,∠AOD=2∠AOB=60°,点P在直径CD上移动,则AP+BP的最小值为 .
17.如图,粮仓的顶部是圆锥形状,这个圆锥的底面圆的半径为3米,母线长为6米,为防雨水,需要在粮仓顶部铺上油毡,如果油毡的市场价为10元/米2,那么购买油毡所需要的费用是 元(结果保留π).
18.如图,圆O是四边形ABCD的内切圆,连接AO、BO、CO、DO,记△AOD、△AOB、△COB、△DOC的面积分别为S1、S2、S3、S4,则S1、S2、S3、S4的数量关系为 .
19.一堆圆锥形沙子,底面直径是8米,高是1.5米,如果每立方米沙子重1.5吨,那么这堆沙子重多少吨?
20.如图,在△ABC中,∠A=60°,∠C=70°,点O是△ABC的内心,BO的延长线交AC于点D,求∠BDC的度数.
21.如图,⊙O是△ABC的外接圆,∠C=30°,AB=2cm,求⊙O的半径.
22.如图,在⊙O中,直径AB=8,∠A=30°,AC=8,AC与⊙O交于点D.
(1)求证:直线BD是线段AC的垂直平分线;
(2)若过点D作DE⊥BC,垂足为E,求证:DE是⊙O的切线;
(3)若点F是AC的三等分点,求BF的长.
23.如图,城市A的正北方向50千米的B处,有一无线电信号发射塔.已知,该发射塔发射的无线电信号的有效半径为100千米,AC是一条直达C城的公路,从A城发往C城的班车速度为60千米/小时.
(1)当班车从A城出发开往C城时,某人立即打开无线电收音机,班车行驶了0.5小时的时候,接收信号最强.此时,班车到发射塔的距离是多少千米?(离发射塔越近,信号越强)
(2)班车从A城到C城共行驶2小时,请你判断到C城后还能接收到信号吗?请说明理由.
24.如图,圆O中两条互相垂直的弦AB,CD交于点E.
(1)M是CD的中点,OM=3,CD=12,求圆O的半径长;
(2)点F在CD上,且CE=EF,求证:AF⊥BD.
25.如图,在⊙O中,弦AB与弦CD相交于点E,且AB=CD.求证:CE=BE.
26.如图,点C在以AB为直径的半圆⊙O上,AC=BC.以B为圆心,以BC的长为半径画圆弧交AB于点D.
(1)求∠ABC的度数;
(2)若AB=2,求阴影部分的面积.
参考答案
1.解:∵正六边形ABCDEF内接于圆O
∴的度数等于360°÷6=60°
∴∠ADB=30°
故选:C.
2.解:∵∠AOC和∠ABC是同弧所对的圆心角和圆周角,
∴∠AOC=2∠ABC=120°;
故选:B.
3.解:根据切线长定理可得:PA=PB,FA=FE,GE=GB;
所以△PFG的周长=PF+FG+PG,
=PF+FE+EG+PG,
=PF+FA+GB+PG,
=PA+PB
=16cm,
故选:C.
4.解:设圆锥的底面半径为r,母线长为R,
∵它的轴截面是正三角形,
∴R=2r,
∴2πr=,
解得n=180°,
故选:D.
5.解:∵OA=OC,
∴∠A=∠ACO=25°,
∴∠BOC=∠A+∠ACO=25°+25°=50°.
故选:B.
6.解:∵⊙O的半径为5,弦AB=8,点C是AB的中点,
∴OC⊥AB,AC=BC=4,OA=5,
∴OC===3,
故选:C.
7.解:∵∠AOB和∠C都对,
∴∠C=∠AOB=×70°=35°.
故选:B.
8.解:∵∠BOD=108°,
∴∠A=∠BOD=54°,
∴∠BCD=180°﹣∠A=126°
故选:C.
9.解:∵OP=5>4,
∴点P与⊙O的位置关系是点在圆外.
故选:C.
10.解:∵BC是⊙O的切线,AB是⊙O的直径,
∴AB⊥BC,
∴∠ABC=90°,
∴∠ACB=90°﹣∠BAC=90°﹣35°=55°.
故选:C.
11.解:连接OA,如图,
∵PA是⊙O的切线,切点为A,
∴OA⊥PA,
∴∠OAP=90°,
∵∠APO=30°,
∴OA=OP=×4=2,
即⊙O的半径长为2.
故选:C.
12.解:扇形面积=,
故选:D.
13.解:连接OE、OB,延长EO交AB于F;
∴E是切点,
∴OE⊥CD,
∴OF⊥AB,OE=OB;
设OB=R,则OF=2﹣R,
在Rt△OBF中,BF=AB=×2=1,OB=R,OF=2﹣R,
∴R2=(2﹣R)2+12,解得R=.
14.解:由题意可得,
扇形的弧长为:=4π(m),
故答案为:4π.
15.解:∵OA=OB,AB=OA,
∴OA=OB=AB,
∴△OAB为等边三角形,
∴∠AOB=60°,
故答案为:60.
16.解:作点A关于CD的对称点A′,连接A′B就是最小值(P此时为A′B与CD的交点),
∵|OA|=|OB|=|OA′|=|CD|=3cm且∠AOD=2∠AOB=60°,
∴∠AOB=∠BOD=30°,
∵A关于CD的对称点A′,
∴∠DOA′=∠AOD=60°,
∴∠BOA′=∠BOD+∠DOA′=90°,
∴△BOA′为等腰直角三角形,
∴AP+BP的最小值为:|A′B|==3cm.
故答案为:3cm.
17.解:根据题意得:圆锥侧面积=π×3×6=18π(平方米),
则购买油毡所需要的费用=10×18π=180π(元).
故答案为:180π.
18.解:如图设切点分别为E、F、G、H,
由切线性质可知,OE⊥AD,OF⊥CD,OG⊥BCOH⊥AB,OE=OF=OG=OH=r,
设DE=DF=a,AE=AH=b,BH=BG=c,CG=CF=d,
S1=r(a+b),S2=r (b+c) S3= r(c+d),S4=r(a+d),
∴S1+S3=r(a+b)+ r(c+d)=r(a+b+c+d),
S2+S4=r(a+d)+r (b+c)=r(a+b+c+d),
∴S1+S3=S2+S4.
故答案为S1+S3=S2+S4.
19.解:这堆沙子重为:π×()2×1.5×1.5=12π(吨),
答:这堆沙子重12π吨.
20.解:∵∠A=60°,∠C=70°,
∴∠ABC=50°,
∵点O为△ABC的内心,
∴∠DBC=∠ABC=25°,
∵∠ACB=70°,∠DBC+∠C+∠BDC=180°,
∴∠BDC=180°﹣70°﹣25°=85°.
21.解:作直径AH,连接BH,
由圆周角定理得,∠ABH=90°,∠H=∠C=30°,
∴AH=2AB=4(cm),
∴⊙O的半径为2cm.
22.解:∵(1)∵AB是⊙O的直径,
∴∠ADB=90°,
∵直径AB=8,∠A=30°,
∴BD=4,AD=4,
∵AC=8,
∴AD=AC,
∴直线BD是线段AC的垂直平分线;
(2)连接OD,
∵D,O分别是线段AC,AB的中点,
∴OD∥BC,OD=BC,
∵DE⊥BC,
∴∠DEC=∠EDO=90°,
∴OD⊥DE,
∴DE是⊙O的切线;
(3)∵点F是AC的三等分点,
∴AF=,
∵AD=4,
∴DF=,
∵BD⊥AC,BD=4,
∴BF==.
23.解:(1)过点B作BM⊥AC于点M,
设班车行驶了0.5小时的时候到达M点.根据此时接受信号最强,则BM⊥AC,又AM=30千米,AB=50千米.
所以BM=40千米.
答:车到发射塔的距离是40千米.
(2)连接BC,
∵AC=60×2=120(千米),AM=30千米,
∴CM=AC﹣AM=90(千米),
∴BC==10<100.
答:到C城能接到信号.
24.解:(1)连接OD,如图:
∵M是CD的中点,CD=12,
∴DM=CD=6,OM⊥CD,∠OMD=90°,
Rt△OMD中,OD=,且OM=3,
∴OD==3,即圆O的半径长为3;
(2)连接AC,延长AF交BD于G,如图:
∵AB⊥CD,CE=EF,
∴AB是CF的垂直平分线,
∴AF=AC,即△ACF是等腰三角形,
∵CE=EF,
∴∠FAE=∠CAE,
∵=,
∴∠CAE=∠CDB,
∴∠FAE=∠CDB,
Rt△BDE中,∠CDB+∠B=90°,
∴∠FAE+∠B=90°,
∴∠AGB=90°,
∴AG⊥BD,即AF⊥BD.
25.证明:∵AB=CD,
∴=,
∴﹣=﹣,即=,
∴∠C=∠B,
∴CE=BE.
26.解:(1)∵AB为半圆⊙O的直径,
∴∠ACB=90°,
∵AC=BC,
∴∠ABC=45°;
(2)∵AB=2,
∴OA=OB=OC=1,BC=,
∴阴影部分的面积=2×1﹣=1﹣
1.如图所示,正六边形ABCDEF内接于圆O,则∠ADB的度数为( )
A.60° B.45° C.30° D.22.5°
2.如图,△ABC是⊙O的内接三角形,若∠ABC=60°,则∠AOC的大小是( )
A.30° B.120° C.135° D.150°
3.如图,PA、PB切⊙O于点A、B,直线FG切⊙O于点E,交PA于F,交PB于点G,若PA=8cm,则△PFG的周长是( )
A.8cm B.12cm C.16cm D.20cm
4.圆锥的截面是一个等边三角形,则它的侧面展开图圆心角度数是( )
A.60° B.90° C.120° D.180°
5.如图,在⊙O中,AB是直径,AC是弦,连接OC,若∠ACO=25°,则∠BOC的度数是( )
A.40° B.50° C.55° D.60°
6.如图,⊙O的半径为5,弦AB=8,点C是AB的中点,连接OC,则OC的长为( )
A.1 B.2 C.3 D.4
7.如图,A,B,C是⊙O上的三点,若∠O=70°,则∠C的度数是( )
A.40° B.35° C.30° D.25°
8.如图,四边形ABCD内接于圆O,∠BOD=108°,则∠BCD的度数是( )
A.127° B.108° C.126° D.125°
9.⊙O的半径为4cm,点P到圆心O的距离为5cm,点P与⊙O的位置关系是( )
A.点P在⊙O内 B.点P在⊙O上 C.点P在⊙O外 D.无法确定
10.如图,AB是⊙O的直径,BC是⊙O的切线,若∠BAC=35°,则∠ACB的大小为( )
A.35° B.45° C.55° D.65°
11.如图,PA是⊙O的切线,切点为A,OP=4,∠APO=30°,则⊙O的半径长为( )
A.1 B. C.2 D.3
12.已知扇形的半径为6,圆心角为150°,则它的面积是( )
A.π B.3π C.5π D.15π
13.已知⊙O过正方形ABCD顶点A、B,且与CD相切,若正方形边长为2,则圆的半径为 .
14.如图,为了美化校园,学校在一块靠墙角的空地上建造了一个扇形花圃,其圆心角AOB=120°,半径为6m,则扇形的弧长是 m.(结果保留π)
15.如图,AB是⊙O的弦,连接OA,OB.若AB=OA=2,则∠AOB= 度.
16.如图,⊙O的直径CD为6cm,OA,OB都是⊙O的半径,∠AOD=2∠AOB=60°,点P在直径CD上移动,则AP+BP的最小值为 .
17.如图,粮仓的顶部是圆锥形状,这个圆锥的底面圆的半径为3米,母线长为6米,为防雨水,需要在粮仓顶部铺上油毡,如果油毡的市场价为10元/米2,那么购买油毡所需要的费用是 元(结果保留π).
18.如图,圆O是四边形ABCD的内切圆,连接AO、BO、CO、DO,记△AOD、△AOB、△COB、△DOC的面积分别为S1、S2、S3、S4,则S1、S2、S3、S4的数量关系为 .
19.一堆圆锥形沙子,底面直径是8米,高是1.5米,如果每立方米沙子重1.5吨,那么这堆沙子重多少吨?
20.如图,在△ABC中,∠A=60°,∠C=70°,点O是△ABC的内心,BO的延长线交AC于点D,求∠BDC的度数.
21.如图,⊙O是△ABC的外接圆,∠C=30°,AB=2cm,求⊙O的半径.
22.如图,在⊙O中,直径AB=8,∠A=30°,AC=8,AC与⊙O交于点D.
(1)求证:直线BD是线段AC的垂直平分线;
(2)若过点D作DE⊥BC,垂足为E,求证:DE是⊙O的切线;
(3)若点F是AC的三等分点,求BF的长.
23.如图,城市A的正北方向50千米的B处,有一无线电信号发射塔.已知,该发射塔发射的无线电信号的有效半径为100千米,AC是一条直达C城的公路,从A城发往C城的班车速度为60千米/小时.
(1)当班车从A城出发开往C城时,某人立即打开无线电收音机,班车行驶了0.5小时的时候,接收信号最强.此时,班车到发射塔的距离是多少千米?(离发射塔越近,信号越强)
(2)班车从A城到C城共行驶2小时,请你判断到C城后还能接收到信号吗?请说明理由.
24.如图,圆O中两条互相垂直的弦AB,CD交于点E.
(1)M是CD的中点,OM=3,CD=12,求圆O的半径长;
(2)点F在CD上,且CE=EF,求证:AF⊥BD.
25.如图,在⊙O中,弦AB与弦CD相交于点E,且AB=CD.求证:CE=BE.
26.如图,点C在以AB为直径的半圆⊙O上,AC=BC.以B为圆心,以BC的长为半径画圆弧交AB于点D.
(1)求∠ABC的度数;
(2)若AB=2,求阴影部分的面积.
参考答案
1.解:∵正六边形ABCDEF内接于圆O
∴的度数等于360°÷6=60°
∴∠ADB=30°
故选:C.
2.解:∵∠AOC和∠ABC是同弧所对的圆心角和圆周角,
∴∠AOC=2∠ABC=120°;
故选:B.
3.解:根据切线长定理可得:PA=PB,FA=FE,GE=GB;
所以△PFG的周长=PF+FG+PG,
=PF+FE+EG+PG,
=PF+FA+GB+PG,
=PA+PB
=16cm,
故选:C.
4.解:设圆锥的底面半径为r,母线长为R,
∵它的轴截面是正三角形,
∴R=2r,
∴2πr=,
解得n=180°,
故选:D.
5.解:∵OA=OC,
∴∠A=∠ACO=25°,
∴∠BOC=∠A+∠ACO=25°+25°=50°.
故选:B.
6.解:∵⊙O的半径为5,弦AB=8,点C是AB的中点,
∴OC⊥AB,AC=BC=4,OA=5,
∴OC===3,
故选:C.
7.解:∵∠AOB和∠C都对,
∴∠C=∠AOB=×70°=35°.
故选:B.
8.解:∵∠BOD=108°,
∴∠A=∠BOD=54°,
∴∠BCD=180°﹣∠A=126°
故选:C.
9.解:∵OP=5>4,
∴点P与⊙O的位置关系是点在圆外.
故选:C.
10.解:∵BC是⊙O的切线,AB是⊙O的直径,
∴AB⊥BC,
∴∠ABC=90°,
∴∠ACB=90°﹣∠BAC=90°﹣35°=55°.
故选:C.
11.解:连接OA,如图,
∵PA是⊙O的切线,切点为A,
∴OA⊥PA,
∴∠OAP=90°,
∵∠APO=30°,
∴OA=OP=×4=2,
即⊙O的半径长为2.
故选:C.
12.解:扇形面积=,
故选:D.
13.解:连接OE、OB,延长EO交AB于F;
∴E是切点,
∴OE⊥CD,
∴OF⊥AB,OE=OB;
设OB=R,则OF=2﹣R,
在Rt△OBF中,BF=AB=×2=1,OB=R,OF=2﹣R,
∴R2=(2﹣R)2+12,解得R=.
14.解:由题意可得,
扇形的弧长为:=4π(m),
故答案为:4π.
15.解:∵OA=OB,AB=OA,
∴OA=OB=AB,
∴△OAB为等边三角形,
∴∠AOB=60°,
故答案为:60.
16.解:作点A关于CD的对称点A′,连接A′B就是最小值(P此时为A′B与CD的交点),
∵|OA|=|OB|=|OA′|=|CD|=3cm且∠AOD=2∠AOB=60°,
∴∠AOB=∠BOD=30°,
∵A关于CD的对称点A′,
∴∠DOA′=∠AOD=60°,
∴∠BOA′=∠BOD+∠DOA′=90°,
∴△BOA′为等腰直角三角形,
∴AP+BP的最小值为:|A′B|==3cm.
故答案为:3cm.
17.解:根据题意得:圆锥侧面积=π×3×6=18π(平方米),
则购买油毡所需要的费用=10×18π=180π(元).
故答案为:180π.
18.解:如图设切点分别为E、F、G、H,
由切线性质可知,OE⊥AD,OF⊥CD,OG⊥BCOH⊥AB,OE=OF=OG=OH=r,
设DE=DF=a,AE=AH=b,BH=BG=c,CG=CF=d,
S1=r(a+b),S2=r (b+c) S3= r(c+d),S4=r(a+d),
∴S1+S3=r(a+b)+ r(c+d)=r(a+b+c+d),
S2+S4=r(a+d)+r (b+c)=r(a+b+c+d),
∴S1+S3=S2+S4.
故答案为S1+S3=S2+S4.
19.解:这堆沙子重为:π×()2×1.5×1.5=12π(吨),
答:这堆沙子重12π吨.
20.解:∵∠A=60°,∠C=70°,
∴∠ABC=50°,
∵点O为△ABC的内心,
∴∠DBC=∠ABC=25°,
∵∠ACB=70°,∠DBC+∠C+∠BDC=180°,
∴∠BDC=180°﹣70°﹣25°=85°.
21.解:作直径AH,连接BH,
由圆周角定理得,∠ABH=90°,∠H=∠C=30°,
∴AH=2AB=4(cm),
∴⊙O的半径为2cm.
22.解:∵(1)∵AB是⊙O的直径,
∴∠ADB=90°,
∵直径AB=8,∠A=30°,
∴BD=4,AD=4,
∵AC=8,
∴AD=AC,
∴直线BD是线段AC的垂直平分线;
(2)连接OD,
∵D,O分别是线段AC,AB的中点,
∴OD∥BC,OD=BC,
∵DE⊥BC,
∴∠DEC=∠EDO=90°,
∴OD⊥DE,
∴DE是⊙O的切线;
(3)∵点F是AC的三等分点,
∴AF=,
∵AD=4,
∴DF=,
∵BD⊥AC,BD=4,
∴BF==.
23.解:(1)过点B作BM⊥AC于点M,
设班车行驶了0.5小时的时候到达M点.根据此时接受信号最强,则BM⊥AC,又AM=30千米,AB=50千米.
所以BM=40千米.
答:车到发射塔的距离是40千米.
(2)连接BC,
∵AC=60×2=120(千米),AM=30千米,
∴CM=AC﹣AM=90(千米),
∴BC==10<100.
答:到C城能接到信号.
24.解:(1)连接OD,如图:
∵M是CD的中点,CD=12,
∴DM=CD=6,OM⊥CD,∠OMD=90°,
Rt△OMD中,OD=,且OM=3,
∴OD==3,即圆O的半径长为3;
(2)连接AC,延长AF交BD于G,如图:
∵AB⊥CD,CE=EF,
∴AB是CF的垂直平分线,
∴AF=AC,即△ACF是等腰三角形,
∵CE=EF,
∴∠FAE=∠CAE,
∵=,
∴∠CAE=∠CDB,
∴∠FAE=∠CDB,
Rt△BDE中,∠CDB+∠B=90°,
∴∠FAE+∠B=90°,
∴∠AGB=90°,
∴AG⊥BD,即AF⊥BD.
25.证明:∵AB=CD,
∴=,
∴﹣=﹣,即=,
∴∠C=∠B,
∴CE=BE.
26.解:(1)∵AB为半圆⊙O的直径,
∴∠ACB=90°,
∵AC=BC,
∴∠ABC=45°;
(2)∵AB=2,
∴OA=OB=OC=1,BC=,
∴阴影部分的面积=2×1﹣=1﹣
同课章节目录
