2021-2022学年人教版九年级数学下册第27章相似期末综合复习训练(word解析版)
文档属性
| 名称 | 2021-2022学年人教版九年级数学下册第27章相似期末综合复习训练(word解析版) |  | |
| 格式 | doc | ||
| 文件大小 | 207.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-26 15:23:03 | ||
图片预览



文档简介
2021-2022学年人教版九年级数学下册《第27章相似》期末综合复习训练2(附答案)
1.下列形状分别为正方形、矩形、正三角形、圆的边框,其中不一定是相似图形的是( )
A. B. C. D.
2.已知=,则的值为( )
A. B. C. D.
3.A、B两地的实际距离AB=250米,如果画在地图上的距离A′B′=5厘米,那么地图上的距离与实际距离的比为( )
A.1:500 B.1:5000 C.500:1 D.5000:1
4.若a、b、c、d是成比例线段,其中a=5,b=2.5,c=8,则线段d的长为( )
A.2 B.4 C.5 D.6
5.如图,在△ABC中,DE∥BC,若AD=2,AB=3,则等于( )
A. B. C. D.
6.如果两个相似三角形的相似比为4:3,那么这两个相似三角形的面积比为( )
A.2: B.4:3 C.16:9 D.256:81
7.如图,已知∠1=∠2,添加下列条件后,仍无法判定△ABC∽△ADE的是( )
A.= B.∠B=∠D C.∠C=∠AED D.=
8.如图,已知△AOB与△A1OB1是以点O为位似中心的位似图形.且相似比为1:2,点B的坐标为(﹣2,4),则点B1的坐标为( )
A.(4,﹣8) B.(2,﹣4) C.(﹣1,8) D.(﹣8,4)
9.如图,在 ABCD中,点O是对角线BD上的一点,且,连接CO并延长交AD于点E,若△COD的面积是2,则四边形ABOE的面积是( )
A.3 B.4 C.5 D.6
10.如图,在圆形花圃中有两条笔直的小径,两端都在花圃边界上,分别记为AC,BD,设交点为P,点C,D之间有一座假山,为了测量C,D之间的距离,小明已经测量了线段AP和PD的长度,只需再测量一条线段的长度,就可以计算C,D之间的距离.小明应该测量的是( )
A.线段BP B.线段CP C.线段AB D.线段AD
11.若两个相似三角形的面积比为9:25,则这两个相似三角形的周长比是 .
12.如图,已知AC∥EF∥BD.如果AE:EB=2:3,CF=6.那么CD的长等于 .
13.如图,△DEF与△ABC位似,点O为位似中心,已知OF:OC=1:2,则△DEF与△ABC的周长之比是 .
14.如图,在△ABC中,点D、E分别在边AB、AC上,∠AED=∠B,如果AD=2,AE=3,CE=1,那么BD长为 .
15.在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣2,4),B(﹣3,1),C(﹣2,0),以原点O为位似中心,把△ABC缩小为原来的,得到△A'B'C′,则点A的对应点A'的坐标为 .
16.如图,为了测量某古城墙的高度,数学兴趣小组根据光的反射定律,把一面镜子放在离古城墙(CD)16m的点P处,然后观测者沿着直线DP后退到点B处.这时恰好在镜子里看到城墙顶端C,并量得BP=3m.已知观测者目高AB=1.5m,那么该古城墙(CD)的高度是 m.
17.如图,△ABC中,AB=8cm,AC=16cm,点P从A出发,以每秒1厘米的速度向B运动,点Q从C同时出发,以每秒2厘米的速度向A运动.其中一个动点到达端点时,另一个也相应停止运动.那么,当以A、P、Q为顶点的三角形与△ABC相似时,运动时间是 .
18.如图,已知O是坐标原点,AB两点的坐标分别为(3,﹣1),(2,1).
(1)以点O为位似中心,在y轴的左侧将△OAB放大2倍;
(2)分别写出A,B两点的对应点A',B'的坐标.
19.某数学兴趣小组想用所学的知识测量小河的宽.测量时,他们选择了河对岸的一棵大树,将其底部作为点A,在他们所在的岸边选择了点B,使得AB与河岸垂直,并在B点竖起标杆BC,再在AB的延长线上选择点D,竖起标杆DE,使得点E,C,A共线.测得BC=1m,DE=1.5m,BD=7m(测量示意图如图所示).请根据相关测量信息,求河宽AB.
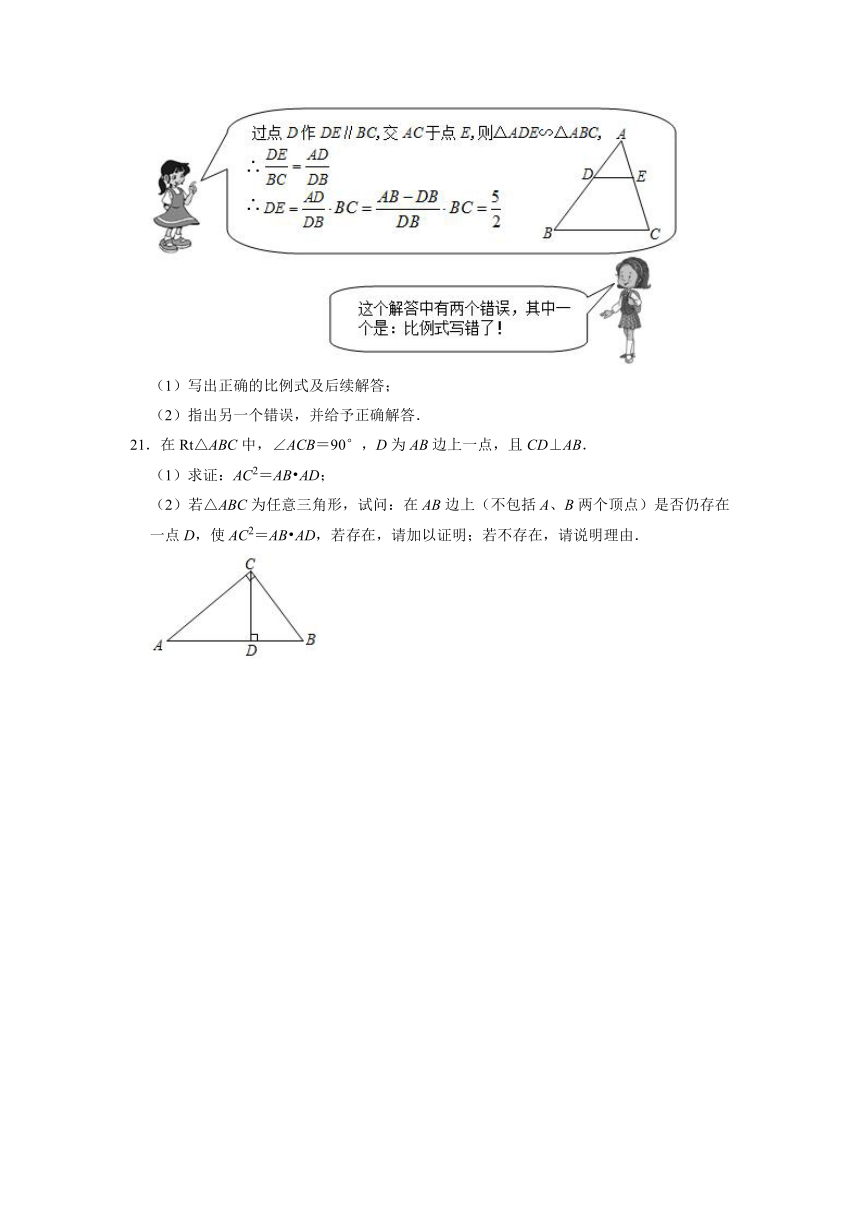
20.在△ABC中,AB=6,BC=5,AC=4,D是线段AB上一点,且DB=4,过点D作DE与线段AC相交于点E,使以A,D,E为顶点的三角形与△ABC相似,求DE的长.请根据下列两位同学的交流回答问题:
(1)写出正确的比例式及后续解答;
(2)指出另一个错误,并给予正确解答.
21.在Rt△ABC中,∠ACB=90°,D为AB边上一点,且CD⊥AB.
(1)求证:AC2=AB AD;
(2)若△ABC为任意三角形,试问:在AB边上(不包括A、B两个顶点)是否仍存在一点D,使AC2=AB AD,若存在,请加以证明;若不存在,请说明理由.
参考答案
1.解:A、两图形形状相同,是相似图形,不符合题意;
B、两图形形状不同,不是相似图形,符合题意;
C、两图形形状相同,是相似图形,不符合题意;
D、两图形形状相同,是相似图形,不符合题意;
故选:B.
2.解:∵=,
∴=+1=+1=;
故选:B.
3.解:取米作为共同的长度单位,那么AB=250米,A'B'=5厘米=0.05米,
所以==,
所以地图上的距离与实际距离的比为1:5000.
故选:B.
4.解:因为a、b、c、d是成比例线段,
可得:,
解得:d=4,
故选:B.
5.解:∵DE∥BC,
∴==.
故选:D.
6.解:∵两个相似三角形的相似比为4:3,
∴这两个相似三角形的面积比为16:9.
故选:C.
7.解:∵∠1=∠2,
∴∠DAE=∠BAC,
若,∠DAE=∠BAC,
∴△ABC∽△ADE,故A不符合题意;
若∠DAE=∠BAC,∠B=∠D,
∴△ABC∽△ADE,故B不符合题意;
若∠C=∠AED,∠DAE=∠BAC,
∴△ABC∽△ADE,故C不符合题意;
∵,∠DAE=∠BAC,
∴无法判断△ABC与△ADE相似,故D符合题意;
故选:D.
8.解:∵△AOB与△A1OB1是以点O为位似中心的位似图形.且相似比为1:2,点B的坐标为(﹣2,4),
∴点B1的坐标为:(﹣2×(﹣2),4×(﹣2))即(4,﹣8).
故选:A.
9.解:∵,△COD的面积是2,
∴△BOC的面积为4,
∵四边形ABCD是平行四边形,
∴AD∥BC,S△ABD=S△BCD=2+4=6,
∴△DOE∽△BOC,
∴=()2=,
∴S△DOE=1,
∴四边形ABOE的面积=6﹣1=5,
故选:C.
10.解:如图,连接AB.
∵∠DCP=∠ABP,∠DPC=∠APB,
∴△APB∽△DPC,
∴AP:DP=AB:DC.
∴只需再测量AB线段的长度,就可以计算C,D之间的距离.
故选:C.
11.解:∵两个相似三角形的面积比为9:25,
∴两个相似三角形的相似比为3:5,
∴这两个相似三角形的周长比为3:5.
故答案为:3:5.
12.解:∵AC∥EF∥BD,
∴==,
∴FD=CF=×6=9,
∴CD=CF+FD=6+9=15.
故答案为15.
13.解:∵△DEF与△ABC位似,点O为位似中心,
∴△DEF与△ABC的周长之比是:1:2.
故答案为:1:2.
14.解:∵∠AED=∠B,∠DAE=∠CAB,
∴△AED∽△ABC,
∴=,
∴=,
解得BD=4.
故答案为:4.
15.解:∵,△ABC的三个顶点坐标分别为A(﹣2,4),B(﹣3,1),C(﹣2,0),以原点O为位似中心,把△ABC缩小为原来的,得到△A'B'C′,
∴点A的对应点A'的坐标为:(﹣2×,4×)或[﹣2×(﹣),4×(﹣)],即(1,﹣2)或(﹣1,2).
故答案为:(1,﹣2)或(﹣1,2).
16.解:由题意知∠CPD=∠APB,∠CDP=∠ABP=90°,
∴△CPD∽△APB.
∴=,
BP=3m.AB=1.5m,DP=16m,
∴=,
∴CD=8(m).
故答案为:8.
17.解:∵点P从A出发,以每秒1厘米的速度向B运动,点Q从C同时出发,以每秒2厘米的速度向A运动.
∴AP=t,CQ=2t,AQ=16﹣2t,
∵∠BAC=∠PAQ,且以A、P、Q为顶点的三角形与△ABC相似,
∴或,
∴或
∴t=4或
故答案为:4或
18.解:(1)如图所示:△OA′B′,即为所求;
(2)A'的坐标是(﹣6,2),B'的坐标是(﹣4,﹣2).
19.解:∵BC∥DE,
∴△ABC∽△ADE,
∴=,
∴=,
∴AB=14(m),
经检验:AB=14是分式方程的解,
答:河宽AB的长为14米.
20.解(1),
∴=.
(2)另一个错在没有进行分类讨论,如图,过点D作∠ADE=∠ACB,
则△ADE∽△ACB,
∴,
∴=.
综合以上可得,DE=或.
21.(1)证明:∵CD⊥AB,
∴∠ADC=∠ACB=90°,
∵∠A=∠A,
∴△ACD∽△ABC,
∴=,
∴AC2=AB AD;
(2)解:存在,
理由:如图,
过C作∠ACD=∠B交AB于D,
则AC2=AB AD,
证明:∵∠ACD=∠B,∠A=∠A,
∴△ACD∽△ABC,
∴=,
∴AC2=AB AD.
1.下列形状分别为正方形、矩形、正三角形、圆的边框,其中不一定是相似图形的是( )
A. B. C. D.
2.已知=,则的值为( )
A. B. C. D.
3.A、B两地的实际距离AB=250米,如果画在地图上的距离A′B′=5厘米,那么地图上的距离与实际距离的比为( )
A.1:500 B.1:5000 C.500:1 D.5000:1
4.若a、b、c、d是成比例线段,其中a=5,b=2.5,c=8,则线段d的长为( )
A.2 B.4 C.5 D.6
5.如图,在△ABC中,DE∥BC,若AD=2,AB=3,则等于( )
A. B. C. D.
6.如果两个相似三角形的相似比为4:3,那么这两个相似三角形的面积比为( )
A.2: B.4:3 C.16:9 D.256:81
7.如图,已知∠1=∠2,添加下列条件后,仍无法判定△ABC∽△ADE的是( )
A.= B.∠B=∠D C.∠C=∠AED D.=
8.如图,已知△AOB与△A1OB1是以点O为位似中心的位似图形.且相似比为1:2,点B的坐标为(﹣2,4),则点B1的坐标为( )
A.(4,﹣8) B.(2,﹣4) C.(﹣1,8) D.(﹣8,4)
9.如图,在 ABCD中,点O是对角线BD上的一点,且,连接CO并延长交AD于点E,若△COD的面积是2,则四边形ABOE的面积是( )
A.3 B.4 C.5 D.6
10.如图,在圆形花圃中有两条笔直的小径,两端都在花圃边界上,分别记为AC,BD,设交点为P,点C,D之间有一座假山,为了测量C,D之间的距离,小明已经测量了线段AP和PD的长度,只需再测量一条线段的长度,就可以计算C,D之间的距离.小明应该测量的是( )
A.线段BP B.线段CP C.线段AB D.线段AD
11.若两个相似三角形的面积比为9:25,则这两个相似三角形的周长比是 .
12.如图,已知AC∥EF∥BD.如果AE:EB=2:3,CF=6.那么CD的长等于 .
13.如图,△DEF与△ABC位似,点O为位似中心,已知OF:OC=1:2,则△DEF与△ABC的周长之比是 .
14.如图,在△ABC中,点D、E分别在边AB、AC上,∠AED=∠B,如果AD=2,AE=3,CE=1,那么BD长为 .
15.在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣2,4),B(﹣3,1),C(﹣2,0),以原点O为位似中心,把△ABC缩小为原来的,得到△A'B'C′,则点A的对应点A'的坐标为 .
16.如图,为了测量某古城墙的高度,数学兴趣小组根据光的反射定律,把一面镜子放在离古城墙(CD)16m的点P处,然后观测者沿着直线DP后退到点B处.这时恰好在镜子里看到城墙顶端C,并量得BP=3m.已知观测者目高AB=1.5m,那么该古城墙(CD)的高度是 m.
17.如图,△ABC中,AB=8cm,AC=16cm,点P从A出发,以每秒1厘米的速度向B运动,点Q从C同时出发,以每秒2厘米的速度向A运动.其中一个动点到达端点时,另一个也相应停止运动.那么,当以A、P、Q为顶点的三角形与△ABC相似时,运动时间是 .
18.如图,已知O是坐标原点,AB两点的坐标分别为(3,﹣1),(2,1).
(1)以点O为位似中心,在y轴的左侧将△OAB放大2倍;
(2)分别写出A,B两点的对应点A',B'的坐标.
19.某数学兴趣小组想用所学的知识测量小河的宽.测量时,他们选择了河对岸的一棵大树,将其底部作为点A,在他们所在的岸边选择了点B,使得AB与河岸垂直,并在B点竖起标杆BC,再在AB的延长线上选择点D,竖起标杆DE,使得点E,C,A共线.测得BC=1m,DE=1.5m,BD=7m(测量示意图如图所示).请根据相关测量信息,求河宽AB.
20.在△ABC中,AB=6,BC=5,AC=4,D是线段AB上一点,且DB=4,过点D作DE与线段AC相交于点E,使以A,D,E为顶点的三角形与△ABC相似,求DE的长.请根据下列两位同学的交流回答问题:
(1)写出正确的比例式及后续解答;
(2)指出另一个错误,并给予正确解答.
21.在Rt△ABC中,∠ACB=90°,D为AB边上一点,且CD⊥AB.
(1)求证:AC2=AB AD;
(2)若△ABC为任意三角形,试问:在AB边上(不包括A、B两个顶点)是否仍存在一点D,使AC2=AB AD,若存在,请加以证明;若不存在,请说明理由.
参考答案
1.解:A、两图形形状相同,是相似图形,不符合题意;
B、两图形形状不同,不是相似图形,符合题意;
C、两图形形状相同,是相似图形,不符合题意;
D、两图形形状相同,是相似图形,不符合题意;
故选:B.
2.解:∵=,
∴=+1=+1=;
故选:B.
3.解:取米作为共同的长度单位,那么AB=250米,A'B'=5厘米=0.05米,
所以==,
所以地图上的距离与实际距离的比为1:5000.
故选:B.
4.解:因为a、b、c、d是成比例线段,
可得:,
解得:d=4,
故选:B.
5.解:∵DE∥BC,
∴==.
故选:D.
6.解:∵两个相似三角形的相似比为4:3,
∴这两个相似三角形的面积比为16:9.
故选:C.
7.解:∵∠1=∠2,
∴∠DAE=∠BAC,
若,∠DAE=∠BAC,
∴△ABC∽△ADE,故A不符合题意;
若∠DAE=∠BAC,∠B=∠D,
∴△ABC∽△ADE,故B不符合题意;
若∠C=∠AED,∠DAE=∠BAC,
∴△ABC∽△ADE,故C不符合题意;
∵,∠DAE=∠BAC,
∴无法判断△ABC与△ADE相似,故D符合题意;
故选:D.
8.解:∵△AOB与△A1OB1是以点O为位似中心的位似图形.且相似比为1:2,点B的坐标为(﹣2,4),
∴点B1的坐标为:(﹣2×(﹣2),4×(﹣2))即(4,﹣8).
故选:A.
9.解:∵,△COD的面积是2,
∴△BOC的面积为4,
∵四边形ABCD是平行四边形,
∴AD∥BC,S△ABD=S△BCD=2+4=6,
∴△DOE∽△BOC,
∴=()2=,
∴S△DOE=1,
∴四边形ABOE的面积=6﹣1=5,
故选:C.
10.解:如图,连接AB.
∵∠DCP=∠ABP,∠DPC=∠APB,
∴△APB∽△DPC,
∴AP:DP=AB:DC.
∴只需再测量AB线段的长度,就可以计算C,D之间的距离.
故选:C.
11.解:∵两个相似三角形的面积比为9:25,
∴两个相似三角形的相似比为3:5,
∴这两个相似三角形的周长比为3:5.
故答案为:3:5.
12.解:∵AC∥EF∥BD,
∴==,
∴FD=CF=×6=9,
∴CD=CF+FD=6+9=15.
故答案为15.
13.解:∵△DEF与△ABC位似,点O为位似中心,
∴△DEF与△ABC的周长之比是:1:2.
故答案为:1:2.
14.解:∵∠AED=∠B,∠DAE=∠CAB,
∴△AED∽△ABC,
∴=,
∴=,
解得BD=4.
故答案为:4.
15.解:∵,△ABC的三个顶点坐标分别为A(﹣2,4),B(﹣3,1),C(﹣2,0),以原点O为位似中心,把△ABC缩小为原来的,得到△A'B'C′,
∴点A的对应点A'的坐标为:(﹣2×,4×)或[﹣2×(﹣),4×(﹣)],即(1,﹣2)或(﹣1,2).
故答案为:(1,﹣2)或(﹣1,2).
16.解:由题意知∠CPD=∠APB,∠CDP=∠ABP=90°,
∴△CPD∽△APB.
∴=,
BP=3m.AB=1.5m,DP=16m,
∴=,
∴CD=8(m).
故答案为:8.
17.解:∵点P从A出发,以每秒1厘米的速度向B运动,点Q从C同时出发,以每秒2厘米的速度向A运动.
∴AP=t,CQ=2t,AQ=16﹣2t,
∵∠BAC=∠PAQ,且以A、P、Q为顶点的三角形与△ABC相似,
∴或,
∴或
∴t=4或
故答案为:4或
18.解:(1)如图所示:△OA′B′,即为所求;
(2)A'的坐标是(﹣6,2),B'的坐标是(﹣4,﹣2).
19.解:∵BC∥DE,
∴△ABC∽△ADE,
∴=,
∴=,
∴AB=14(m),
经检验:AB=14是分式方程的解,
答:河宽AB的长为14米.
20.解(1),
∴=.
(2)另一个错在没有进行分类讨论,如图,过点D作∠ADE=∠ACB,
则△ADE∽△ACB,
∴,
∴=.
综合以上可得,DE=或.
21.(1)证明:∵CD⊥AB,
∴∠ADC=∠ACB=90°,
∵∠A=∠A,
∴△ACD∽△ABC,
∴=,
∴AC2=AB AD;
(2)解:存在,
理由:如图,
过C作∠ACD=∠B交AB于D,
则AC2=AB AD,
证明:∵∠ACD=∠B,∠A=∠A,
∴△ACD∽△ABC,
∴=,
∴AC2=AB AD.
