小学数学北师大版六年级下4.2—4.3正比例 课件(共20张PPT)
文档属性
| 名称 | 小学数学北师大版六年级下4.2—4.3正比例 课件(共20张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-26 08:04:34 | ||
图片预览







文档简介
(共20张PPT)
第2课时 正比例(一)
四 正比例与反比例
一、复习引入
(1)已知路程和时间,怎样求速度?
(2)已知总价和数量,怎样求单价?
(3)已知工作总量和工作时间,怎样求工作效率?
工作效率
单价
=
——
——
——
=
=
二、学习新课
下面是正方形周长与边长、面积与边长之间的变化情况,把表格填写完整,并说说你分别发现了什么。
8
12
4
正方形的面积和周长都是随着边长的增加而增加的。
边长/cm 1 2 3
周长/cm 4
边长/cm 1 2 3
面积/cm2 1
16
4
9
4
16
二、学习新课
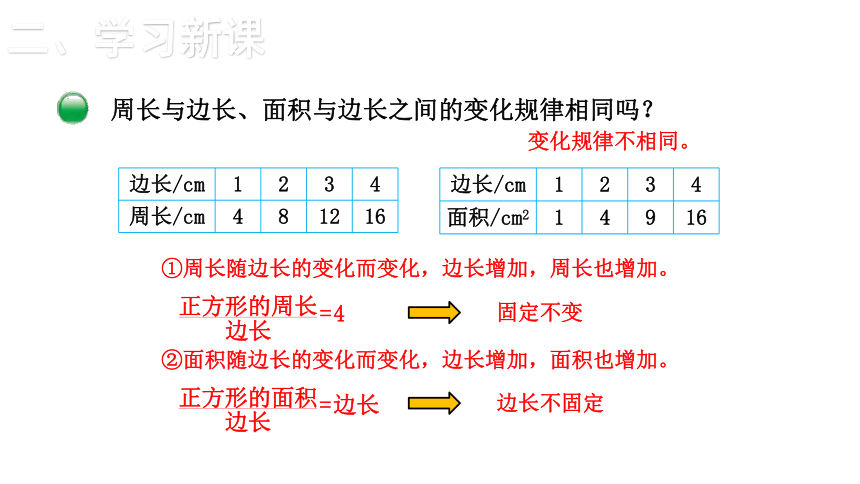
周长与边长、面积与边长之间的变化规律相同吗?
边长/cm 1 2 3 4
周长/cm 4 8 12 16
边长/cm 1 2 3 4
面积/cm2 1 4 9 16
①周长随边长的变化而变化,边长增加,周长也增加。
②面积随边长的变化而变化,边长增加,面积也增加。
固定不变
边长不固定
变化规律不相同。
二、学习新课
一辆汽车以90千米/时的速度行驶,行驶的路程与时间如下。把下表填写完整,你从表中发现了什么?
时间/时 1 2 3 4 5 6 7
路程/km 90 180 270 360
450
540
630
8
720
路程与时间的比值是一定的。
路程是随着时间的变化而变化的,时间增加,路程也随着增加。
路程
时间
=速度
(一定)
二、学习新课
像这样,路程和时间两个量,时间变化,所行驶的路程也随着变化,而且路程与时间的比值(也就是速度)一定,我们就说路程和时间成正比例。
用x和y表示两种相关联的量,用k表示它们的比值。
y
x
=k
(一定)
三、巩固练习
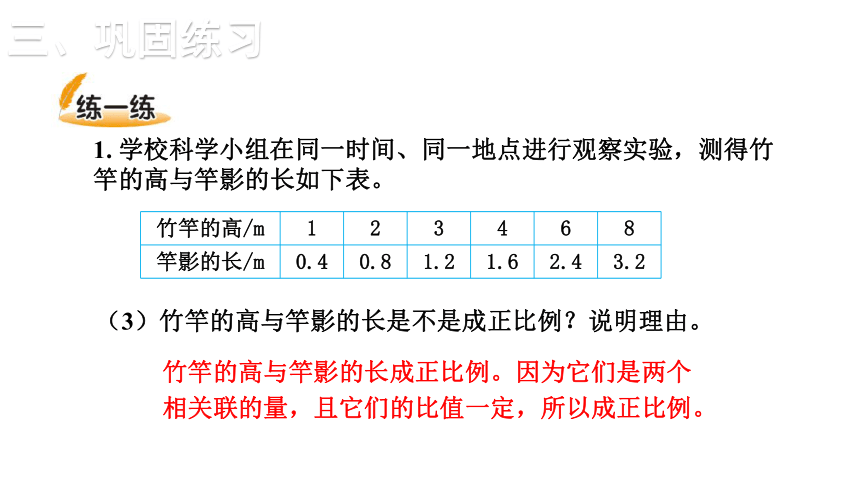
1. 学校科学小组在同一时间、同一地点进行观察实验,测得竹竿的高与竿影的长如下表。
竹竿的高/m 1 2 3 4 6 8
竿影的长/m 0.4 0.8 1.2 1.6 2.4 3.2
(1)说一说竿影的长与竹竿的高的变化关系。
竿影的长随竹竿的高的变化而变化。
当竹竿的高增加时,竿影的长也随之增加。
三、巩固练习
1. 学校科学小组在同一时间、同一地点进行观察实验,测得竹竿的高与竿影的长如下表。
竹竿的高/m 1 2 3 4 6 8
竿影的长/m 0.4 0.8 1.2 1.6 2.4 3.2
(2)写出竿影的长与竹竿的高的比,你有什么发现?
它们的比值一定。
三、巩固练习
1. 学校科学小组在同一时间、同一地点进行观察实验,测得竹竿的高与竿影的长如下表。
竹竿的高/m 1 2 3 4 6 8
竿影的长/m 0.4 0.8 1.2 1.6 2.4 3.2
(3)竹竿的高与竿影的长是不是成正比例?说明理由。
竹竿的高与竿影的长成正比例。因为它们是两个相关联的量,且它们的比值一定,所以成正比例。
四、课堂小结
1.两种相关联的量,一种量变化,另一种量也随着变化。
2.如果这两种量中相对应的两个数的比值(也就是商)一定,就说这两种量成正比例。
3.用x和y表示两种相关联的量,用k表示它们的比值。
y
x
=k
(一定)
正比例(二)
四 正比例与反比例
一、复习引入
说一说正比例的意义。
像这样,路程和时间两个量,时间变化,所行驶的路程也随着变化,而且路程与时间的比值(也就是速度)一定,我们就说路程和时间成正比例。
二、学习新课
圆的面积与半径成正比例吗?你是怎么想的?与同伴交流。
圆的面积 3.14 12.56 28.26
半 径 1 2 3
圆的面积与半径的比值不相等。
圆的面积与半径不成正比例。
二、学习新课
判断两个量是否成正比例的方法
①首先判断两个量是不是相关联的量;②再判断两个量的比值是否固定不变;③最后判断出这两个量是否成正比例。
二、学习新课
乐乐和爸爸的年龄变化情况如下,把表填写完整。
他们的年龄成正比例吗?为什么?
乐乐的年龄/岁 6 7 8 9 10 11
爸爸的年龄/岁 32 33
34
35
36
37
乐乐的年龄和爸爸的年龄是两个相关联的量,但它们的比值不一定,所以乐乐的年龄和爸爸的年龄不成正比例。
二、学习新课
分别举一个成正比例和一个不成正比例的例子,与同伴交流。
单价一定时,数量和总价成正比例。
长方形的宽和面积不成正比例。
三、巩固练习
2.根据下表中底是6 cm的平行四边形的面积与高相对应的数据,判断它们是不是成正比例,并说明理由。
平行四边形的面积/cm2 6 12 18 24 30
平行四边形的高/cm 1 2 3 4 5
面积
高
=底
(比值一定)成正比例
三、巩固练习
3.判断下面各题中的两个量是否成正比例,并说明理由。
(1)每袋大米的质量一定,大米的总质量和袋数。
(2)一个人的身高和年龄。
(3)宽不变,长方形的周长与长。
成正比例
不成正比例
不成正比例
身高与年龄的比值不一定
长方形的周长÷2=长+宽
三、巩固练习
4.把表填完整,你从中发现了什么?应付金额与所买邮票的数量成正比例吗?
买邮票的数量/枚 应付金额/元
1 0.8
2 1.6
3
4
5
6
7
8
2.4
3.2
4
4.8
5.6
6.4
应付金额随买邮票的数量的变化而变化,且应付金额与买邮票的枚数成正比例。
四、课堂小结
判断两个量是否成正比例的方法:
①首先判断两个量是不是相关联的量;
②再判断两个量的比值是否固定不变;
③最后判断出这两个量是否成正比例。
第2课时 正比例(一)
四 正比例与反比例
一、复习引入
(1)已知路程和时间,怎样求速度?
(2)已知总价和数量,怎样求单价?
(3)已知工作总量和工作时间,怎样求工作效率?
工作效率
单价
=
——
——
——
=
=
二、学习新课
下面是正方形周长与边长、面积与边长之间的变化情况,把表格填写完整,并说说你分别发现了什么。
8
12
4
正方形的面积和周长都是随着边长的增加而增加的。
边长/cm 1 2 3
周长/cm 4
边长/cm 1 2 3
面积/cm2 1
16
4
9
4
16
二、学习新课
周长与边长、面积与边长之间的变化规律相同吗?
边长/cm 1 2 3 4
周长/cm 4 8 12 16
边长/cm 1 2 3 4
面积/cm2 1 4 9 16
①周长随边长的变化而变化,边长增加,周长也增加。
②面积随边长的变化而变化,边长增加,面积也增加。
固定不变
边长不固定
变化规律不相同。
二、学习新课
一辆汽车以90千米/时的速度行驶,行驶的路程与时间如下。把下表填写完整,你从表中发现了什么?
时间/时 1 2 3 4 5 6 7
路程/km 90 180 270 360
450
540
630
8
720
路程与时间的比值是一定的。
路程是随着时间的变化而变化的,时间增加,路程也随着增加。
路程
时间
=速度
(一定)
二、学习新课
像这样,路程和时间两个量,时间变化,所行驶的路程也随着变化,而且路程与时间的比值(也就是速度)一定,我们就说路程和时间成正比例。
用x和y表示两种相关联的量,用k表示它们的比值。
y
x
=k
(一定)
三、巩固练习
1. 学校科学小组在同一时间、同一地点进行观察实验,测得竹竿的高与竿影的长如下表。
竹竿的高/m 1 2 3 4 6 8
竿影的长/m 0.4 0.8 1.2 1.6 2.4 3.2
(1)说一说竿影的长与竹竿的高的变化关系。
竿影的长随竹竿的高的变化而变化。
当竹竿的高增加时,竿影的长也随之增加。
三、巩固练习
1. 学校科学小组在同一时间、同一地点进行观察实验,测得竹竿的高与竿影的长如下表。
竹竿的高/m 1 2 3 4 6 8
竿影的长/m 0.4 0.8 1.2 1.6 2.4 3.2
(2)写出竿影的长与竹竿的高的比,你有什么发现?
它们的比值一定。
三、巩固练习
1. 学校科学小组在同一时间、同一地点进行观察实验,测得竹竿的高与竿影的长如下表。
竹竿的高/m 1 2 3 4 6 8
竿影的长/m 0.4 0.8 1.2 1.6 2.4 3.2
(3)竹竿的高与竿影的长是不是成正比例?说明理由。
竹竿的高与竿影的长成正比例。因为它们是两个相关联的量,且它们的比值一定,所以成正比例。
四、课堂小结
1.两种相关联的量,一种量变化,另一种量也随着变化。
2.如果这两种量中相对应的两个数的比值(也就是商)一定,就说这两种量成正比例。
3.用x和y表示两种相关联的量,用k表示它们的比值。
y
x
=k
(一定)
正比例(二)
四 正比例与反比例
一、复习引入
说一说正比例的意义。
像这样,路程和时间两个量,时间变化,所行驶的路程也随着变化,而且路程与时间的比值(也就是速度)一定,我们就说路程和时间成正比例。
二、学习新课
圆的面积与半径成正比例吗?你是怎么想的?与同伴交流。
圆的面积 3.14 12.56 28.26
半 径 1 2 3
圆的面积与半径的比值不相等。
圆的面积与半径不成正比例。
二、学习新课
判断两个量是否成正比例的方法
①首先判断两个量是不是相关联的量;②再判断两个量的比值是否固定不变;③最后判断出这两个量是否成正比例。
二、学习新课
乐乐和爸爸的年龄变化情况如下,把表填写完整。
他们的年龄成正比例吗?为什么?
乐乐的年龄/岁 6 7 8 9 10 11
爸爸的年龄/岁 32 33
34
35
36
37
乐乐的年龄和爸爸的年龄是两个相关联的量,但它们的比值不一定,所以乐乐的年龄和爸爸的年龄不成正比例。
二、学习新课
分别举一个成正比例和一个不成正比例的例子,与同伴交流。
单价一定时,数量和总价成正比例。
长方形的宽和面积不成正比例。
三、巩固练习
2.根据下表中底是6 cm的平行四边形的面积与高相对应的数据,判断它们是不是成正比例,并说明理由。
平行四边形的面积/cm2 6 12 18 24 30
平行四边形的高/cm 1 2 3 4 5
面积
高
=底
(比值一定)成正比例
三、巩固练习
3.判断下面各题中的两个量是否成正比例,并说明理由。
(1)每袋大米的质量一定,大米的总质量和袋数。
(2)一个人的身高和年龄。
(3)宽不变,长方形的周长与长。
成正比例
不成正比例
不成正比例
身高与年龄的比值不一定
长方形的周长÷2=长+宽
三、巩固练习
4.把表填完整,你从中发现了什么?应付金额与所买邮票的数量成正比例吗?
买邮票的数量/枚 应付金额/元
1 0.8
2 1.6
3
4
5
6
7
8
2.4
3.2
4
4.8
5.6
6.4
应付金额随买邮票的数量的变化而变化,且应付金额与买邮票的枚数成正比例。
四、课堂小结
判断两个量是否成正比例的方法:
①首先判断两个量是不是相关联的量;
②再判断两个量的比值是否固定不变;
③最后判断出这两个量是否成正比例。
