小学数学北师大版六年级下第四单元 正比例与反比例 练习四 课件(共25张PPT)
文档属性
| 名称 | 小学数学北师大版六年级下第四单元 正比例与反比例 练习四 课件(共25张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-26 00:00:00 | ||
图片预览





文档简介
(共25张PPT)
第7课时 练习四
四 正比例与反比例
一、复习回顾
知识点 具体内容
变化的量
正比例
画一画
反比例
一、复习回顾
知识点 具体内容
变化的量
两个相关联的量,一个量随着另一个量的变化而变化。
一、复习回顾
知识点 具体内容
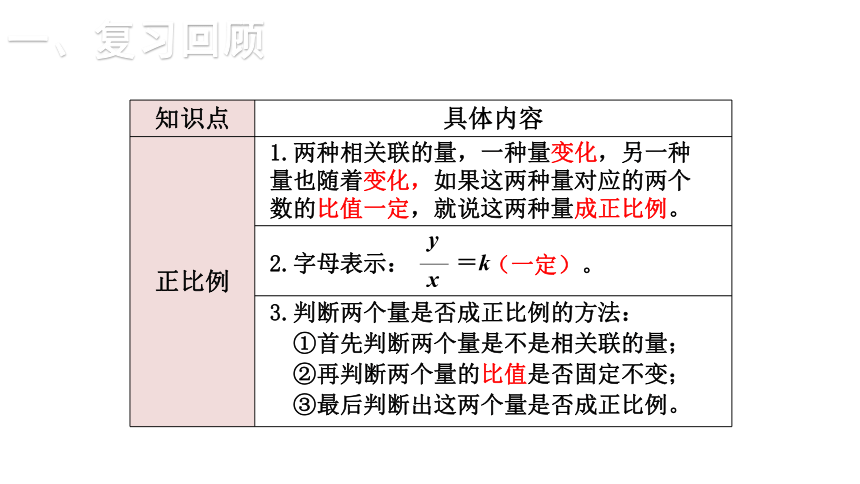
正比例
1.两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量对应的两个数的比值一定,就说这两种量成正比例。
2.字母表示:
3.判断两个量是否成正比例的方法:
①首先判断两个量是不是相关联的量;
②再判断两个量的比值是否固定不变;
③最后判断出这两个量是否成正比例。
y
x
=k
(一定)。
一、复习回顾
知识点 具体内容
画一画
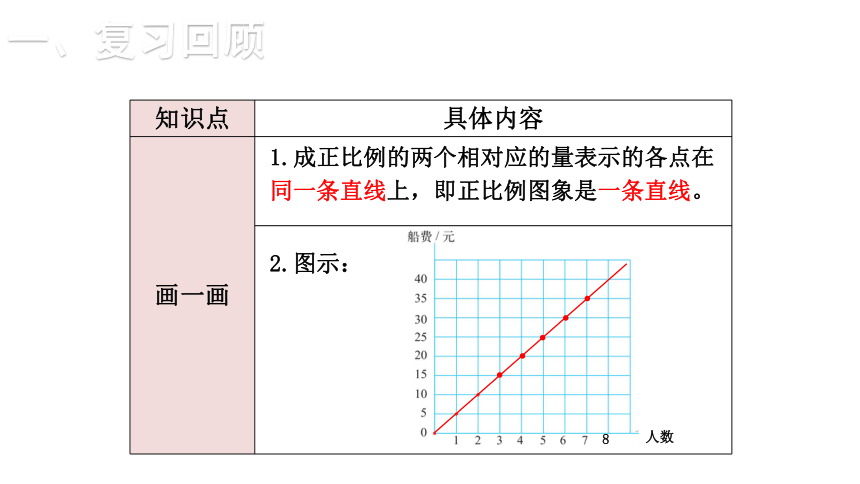
1.成正比例的两个相对应的量表示的各点在同一条直线上,即正比例图象是一条直线。
2.图示:
人数
8
一、复习回顾
知识点 具体内容
反比例
1.两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量对应的两个数的乘积一定,就说这两种量成反比例。
2.字母表示:xy=k(一定)。
3.判断两个量是否成反比例的方法:
①首先判断两个量是不是相关联的量;
②再判断两个量的乘积是否固定不变;
③最后判断出这两个量是否成反比例。
二、指导练习
1.彩带每米售价2元,购买2m,3m……分别需要多少元?
(1)填一填。
练习四
长度/m 0 1 2 3 4 5 6 ……
应付金额/元 0 2 ……
4
6
8
10
12
二、指导练习
(2)判断应付金额与彩带的长度是否成正比例,并说明理由。
练习四
长度/m 0 1 2 3 4 5 6 ……
应付金额/元 0 2 4 6 8 10 12 ……
成正比例。
应付金额
长度
=2
二、指导练习
练习四
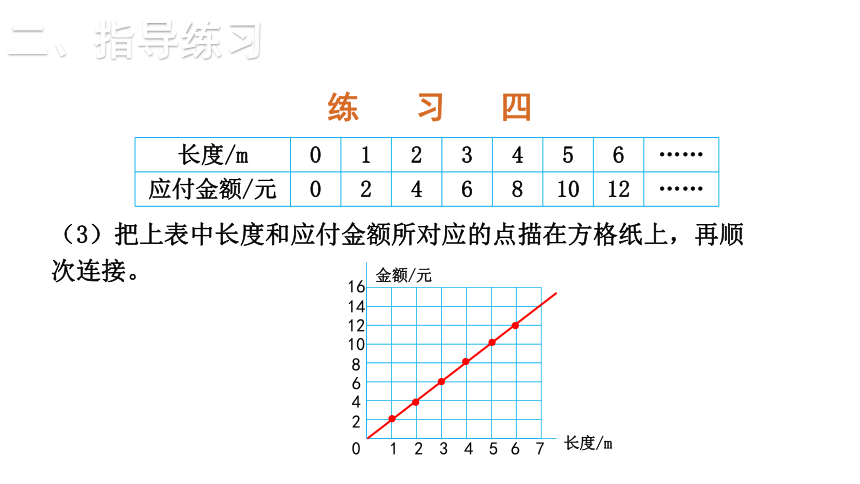
(3)把上表中长度和应付金额所对应的点描在方格纸上,再顺次连接。
长度/m 0 1 2 3 4 5 6 ……
应付金额/元 0 2 4 6 8 10 12 ……
2
0
4
6
8
10
12
14
16
2
1
3
4
5
6
7
长度/m
金额/元
二、指导练习
练习四
(4)买6.5 m彩带大约要花多少元?
长度/m 0 1 2 3 4 5 6 ……
应付金额/元 0 2 4 6 8 10 12 ……
2
0
4
6
8
10
12
14
16
2
1
3
4
5
6
7
长度/m
金额/元
单价:2元/m
6.5×2=13(元)
答:买6.5 m彩带大约要花13元。
二、指导练习
练习四
(5)淘气买的彩带长度是笑笑的3倍,他花的钱是笑笑的几倍?
长度/m 0 1 2 3 4 5 6 ……
应付金额/元 0 2 4 6 8 10 12 ……
2
0
4
6
8
10
12
14
16
2
1
3
4
5
6
7
长度/m
金额/元
他花的钱是笑笑的3倍。
二、指导练习
2.下面各题中的两个量,哪些成正比例,哪些成反比例,哪些既不成正比例也不成反比例?
(1)等边三角形的周长与边长。
(2)妙想从家步行到学校的平均速度与所花的时间。
(3)每年体检,你们班视力正常的人数与近视的人数。
练习四
成正比例
成反比例
既不成正比例也不成反比例
练习四
3.给一间教室铺地砖,每块地砖的面积与所需地砖的数量如下。
每块地砖的面积和所需地砖的数量成反比例。
每块地砖的面积/m2 0.2 0.3 0.4 0.6 0.8 ……
所需地砖的数量/块 600 400 300 200 150 ……
(1)每块地砖的面积和所需地砖的数量有什么关系
二、指导练习
练习四
3.给一间教室铺地砖,每块地砖的面积与所需地砖的数量如下。
0.2×600÷0.5=240(块)
每块地砖的面积/m2 0.2 0.3 0.4 0.6 0.8 ……
所需地砖的数量/块 600 400 300 200 150 ……
(2)如果每块地砖的面积是0.5 m2,铺这一地面需要多少块地砖?
答:铺这一地面需要240块地砖。
二、指导练习
练习四
3.给一间教室铺地砖,每块地砖的面积与所需地砖的数量如下。
每块地砖的面积/m2 0.2 0.3 0.4 0.6 0.8 ……
所需地砖的数量/块 600 400 300 200 150 ……
(3)铺这一地面用了500块地砖,所用的地砖每块面积是多大?
0.2×600÷500=0.24(m2)
答:所用的地砖每块面积是0.24 m2。
二、指导练习
练习四
4.下图中线段OA表示淘气骑车行驶的路程与时间的关系。
请根据左图回答下列问题。
(1)淘气骑车行驶了多长时间?行驶了多少千米?
淘气骑车行驶了2时,行驶了30 km。
二、指导练习
练习四
4.下图中线段OA表示淘气骑车行驶的路程与时间的关系。
(2)骑车1.5 时,淘气行驶了多少千米?
淘气行驶了22.5 km。
二、指导练习
1.5 时
22.5 时
练习四
4.下图中线段OA表示淘气骑车行驶的路程与时间的关系。
(3)行驶30 km,淘气用了多长时间?
淘气用了2 时。
二、指导练习
1.下图中线段OA表示淘气骑车行驶的路程与时间的关系。
(4)淘气骑车的速度是多少?
30÷2=15(千米/时)
答:淘气骑车的速度是15千米/时。
二、指导练习
练习四
练习四
5.用36个边长为1 cm的小正方形,你能拼成几种不同的长方形?
从表中,你能发现长和宽有怎样的关系吗?与同伴进行交流。
长/cm
宽/cm
36
18
12
9
6
1
2
3
4
6
一共能拼成5种不同的长方形。
长×宽=36,长与宽成反比例。
二、指导练习
三、巩固练习
练习
1.选择正确的关系。
(1)平行四边形的面积一定,它的底和高( )。
(2)一条绳子的长度一定,用去的和剩下的( )。
(3)每袋面粉的质量一定,面粉的总质量和袋数( )。
A.成正比例 B.成反比例 C.不成比例
B
C
A
三、巩固练习
练习
2.下图表示某超市出售矿泉水的数量与总价的关系,看图回答下列问题。
(1)矿泉水的总价和数量成( )关系。
(2)5瓶的售价是( )元,1瓶的售价是
( )元。
正比例
10
2
三、巩固练习
练习
3.一个模型组装车间要完成一批任务,每天组装模型的数量与需要的天数如下表。
每天组装的数量/个 500 600 800 1000 1200
需要的天数/天 24 20 15 12 10
(1)每天组装的数量可以称为工作效率,用P表示;需要的天数可以称为工作时间,用t表示。如果组装的手机总数称为工作总量,那么工作总量是多少?
工作总量=工作效率×工作时间=Pt
三、巩固练习
练习
3.一个模型组装车间要完成一批任务,每天组装模型的数量与需要的天数如下表。
每天组装的数量/个 500 600 800 1000 1200
需要的天数/天 24 20 15 12 10
(2)如果每天组装2000个模型,那么需要多少天?
1200×10÷2000=6(天)
答:需要6天。
四、课堂小结
本单元学习了:
1.变化的量。
2.正比例。
3.画一画(正比例的图象)。
4.反比例。
第7课时 练习四
四 正比例与反比例
一、复习回顾
知识点 具体内容
变化的量
正比例
画一画
反比例
一、复习回顾
知识点 具体内容
变化的量
两个相关联的量,一个量随着另一个量的变化而变化。
一、复习回顾
知识点 具体内容
正比例
1.两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量对应的两个数的比值一定,就说这两种量成正比例。
2.字母表示:
3.判断两个量是否成正比例的方法:
①首先判断两个量是不是相关联的量;
②再判断两个量的比值是否固定不变;
③最后判断出这两个量是否成正比例。
y
x
=k
(一定)。
一、复习回顾
知识点 具体内容
画一画
1.成正比例的两个相对应的量表示的各点在同一条直线上,即正比例图象是一条直线。
2.图示:
人数
8
一、复习回顾
知识点 具体内容
反比例
1.两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量对应的两个数的乘积一定,就说这两种量成反比例。
2.字母表示:xy=k(一定)。
3.判断两个量是否成反比例的方法:
①首先判断两个量是不是相关联的量;
②再判断两个量的乘积是否固定不变;
③最后判断出这两个量是否成反比例。
二、指导练习
1.彩带每米售价2元,购买2m,3m……分别需要多少元?
(1)填一填。
练习四
长度/m 0 1 2 3 4 5 6 ……
应付金额/元 0 2 ……
4
6
8
10
12
二、指导练习
(2)判断应付金额与彩带的长度是否成正比例,并说明理由。
练习四
长度/m 0 1 2 3 4 5 6 ……
应付金额/元 0 2 4 6 8 10 12 ……
成正比例。
应付金额
长度
=2
二、指导练习
练习四
(3)把上表中长度和应付金额所对应的点描在方格纸上,再顺次连接。
长度/m 0 1 2 3 4 5 6 ……
应付金额/元 0 2 4 6 8 10 12 ……
2
0
4
6
8
10
12
14
16
2
1
3
4
5
6
7
长度/m
金额/元
二、指导练习
练习四
(4)买6.5 m彩带大约要花多少元?
长度/m 0 1 2 3 4 5 6 ……
应付金额/元 0 2 4 6 8 10 12 ……
2
0
4
6
8
10
12
14
16
2
1
3
4
5
6
7
长度/m
金额/元
单价:2元/m
6.5×2=13(元)
答:买6.5 m彩带大约要花13元。
二、指导练习
练习四
(5)淘气买的彩带长度是笑笑的3倍,他花的钱是笑笑的几倍?
长度/m 0 1 2 3 4 5 6 ……
应付金额/元 0 2 4 6 8 10 12 ……
2
0
4
6
8
10
12
14
16
2
1
3
4
5
6
7
长度/m
金额/元
他花的钱是笑笑的3倍。
二、指导练习
2.下面各题中的两个量,哪些成正比例,哪些成反比例,哪些既不成正比例也不成反比例?
(1)等边三角形的周长与边长。
(2)妙想从家步行到学校的平均速度与所花的时间。
(3)每年体检,你们班视力正常的人数与近视的人数。
练习四
成正比例
成反比例
既不成正比例也不成反比例
练习四
3.给一间教室铺地砖,每块地砖的面积与所需地砖的数量如下。
每块地砖的面积和所需地砖的数量成反比例。
每块地砖的面积/m2 0.2 0.3 0.4 0.6 0.8 ……
所需地砖的数量/块 600 400 300 200 150 ……
(1)每块地砖的面积和所需地砖的数量有什么关系
二、指导练习
练习四
3.给一间教室铺地砖,每块地砖的面积与所需地砖的数量如下。
0.2×600÷0.5=240(块)
每块地砖的面积/m2 0.2 0.3 0.4 0.6 0.8 ……
所需地砖的数量/块 600 400 300 200 150 ……
(2)如果每块地砖的面积是0.5 m2,铺这一地面需要多少块地砖?
答:铺这一地面需要240块地砖。
二、指导练习
练习四
3.给一间教室铺地砖,每块地砖的面积与所需地砖的数量如下。
每块地砖的面积/m2 0.2 0.3 0.4 0.6 0.8 ……
所需地砖的数量/块 600 400 300 200 150 ……
(3)铺这一地面用了500块地砖,所用的地砖每块面积是多大?
0.2×600÷500=0.24(m2)
答:所用的地砖每块面积是0.24 m2。
二、指导练习
练习四
4.下图中线段OA表示淘气骑车行驶的路程与时间的关系。
请根据左图回答下列问题。
(1)淘气骑车行驶了多长时间?行驶了多少千米?
淘气骑车行驶了2时,行驶了30 km。
二、指导练习
练习四
4.下图中线段OA表示淘气骑车行驶的路程与时间的关系。
(2)骑车1.5 时,淘气行驶了多少千米?
淘气行驶了22.5 km。
二、指导练习
1.5 时
22.5 时
练习四
4.下图中线段OA表示淘气骑车行驶的路程与时间的关系。
(3)行驶30 km,淘气用了多长时间?
淘气用了2 时。
二、指导练习
1.下图中线段OA表示淘气骑车行驶的路程与时间的关系。
(4)淘气骑车的速度是多少?
30÷2=15(千米/时)
答:淘气骑车的速度是15千米/时。
二、指导练习
练习四
练习四
5.用36个边长为1 cm的小正方形,你能拼成几种不同的长方形?
从表中,你能发现长和宽有怎样的关系吗?与同伴进行交流。
长/cm
宽/cm
36
18
12
9
6
1
2
3
4
6
一共能拼成5种不同的长方形。
长×宽=36,长与宽成反比例。
二、指导练习
三、巩固练习
练习
1.选择正确的关系。
(1)平行四边形的面积一定,它的底和高( )。
(2)一条绳子的长度一定,用去的和剩下的( )。
(3)每袋面粉的质量一定,面粉的总质量和袋数( )。
A.成正比例 B.成反比例 C.不成比例
B
C
A
三、巩固练习
练习
2.下图表示某超市出售矿泉水的数量与总价的关系,看图回答下列问题。
(1)矿泉水的总价和数量成( )关系。
(2)5瓶的售价是( )元,1瓶的售价是
( )元。
正比例
10
2
三、巩固练习
练习
3.一个模型组装车间要完成一批任务,每天组装模型的数量与需要的天数如下表。
每天组装的数量/个 500 600 800 1000 1200
需要的天数/天 24 20 15 12 10
(1)每天组装的数量可以称为工作效率,用P表示;需要的天数可以称为工作时间,用t表示。如果组装的手机总数称为工作总量,那么工作总量是多少?
工作总量=工作效率×工作时间=Pt
三、巩固练习
练习
3.一个模型组装车间要完成一批任务,每天组装模型的数量与需要的天数如下表。
每天组装的数量/个 500 600 800 1000 1200
需要的天数/天 24 20 15 12 10
(2)如果每天组装2000个模型,那么需要多少天?
1200×10÷2000=6(天)
答:需要6天。
四、课堂小结
本单元学习了:
1.变化的量。
2.正比例。
3.画一画(正比例的图象)。
4.反比例。
