小学数学北师大版六年级下7.总复习 第二部分 图形与几何——图形的认识(二) 课件(共21张PPT)
文档属性
| 名称 | 小学数学北师大版六年级下7.总复习 第二部分 图形与几何——图形的认识(二) 课件(共21张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-26 10:51:10 | ||
图片预览







文档简介
(共21张PPT)
第2课时 图形的认识(二)
总复习
一、回顾整理
【回顾1】线段、射线、直线
线段
直线上两点间的一段叫作线段,线段有两个端点,可以度量长度。
射线
把线段的一端无限延长,就得到一条射线,射线只有一个端点,它是无限长的,不能度量长度。
直线
把线段的两端无限延长,就得到一条直线,直线没有端点,它是无限长的,不能度量长度。
一、回顾整理
【回顾2】角
角的意义
从一点引出两条射线,就组成一个角。角有一个顶点和两条边。
角的分类及大小关系
角包括锐角、直角、钝角、平角、周角等。
锐角<直角<钝角<平角<周角
1周角=2平角=4直角
一、回顾整理
【回顾3】垂直与平行
两条直线相交成直角时,这两条直线互相垂直。其中一条直线叫作另一条直线的垂线,这两条直线的交点叫作垂足。
在同一平面内,不相交的两条直线叫作平行线。
垂直、垂线与垂足
平行线
二、知识应用
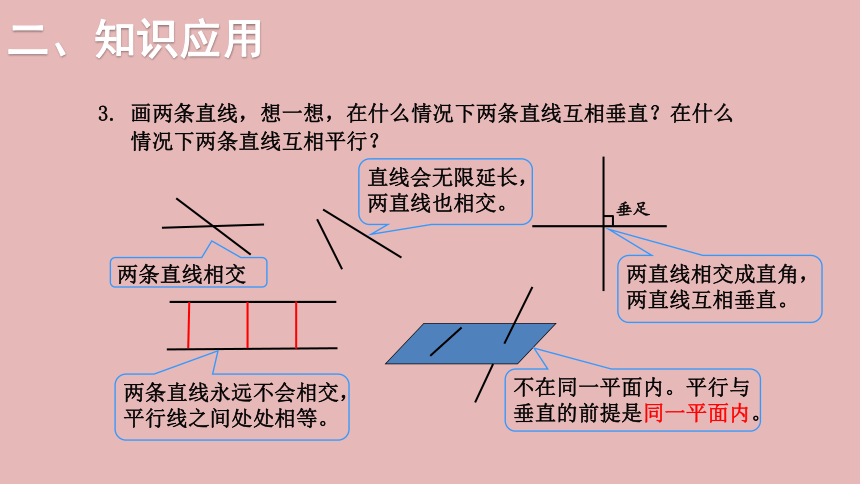
3. 画两条直线,想一想,在什么情况下两条直线互相垂直?在什么
情况下两条直线互相平行?
垂足
两条直线相交
直线会无限延长,两直线也相交。
两直线相交成直角,两直线互相垂直。
两条直线永远不会相交,平行线之间处处相等。
不在同一平面内。平行与垂直的前提是同一平面内。
二、知识应用
同一平面内,不相交的两直线平行。若两直线相交所成角为90°,则两直线垂直。
平行线间的距离处处相等。
二、知识应用
顶点
边
边
角的组成
二、知识应用
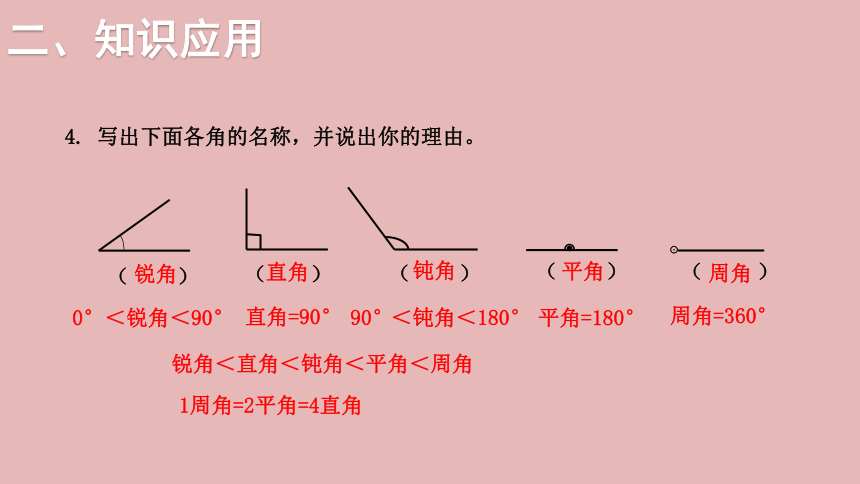
4. 写出下面各角的名称,并说出你的理由。
( )
( )
( )
●
⌒
( )
⊙
( )
锐角
直角
钝角
平角
周角
0°<锐角<90°
直角=90°
90°<钝角<180°
平角=180°
周角=360°
锐角<直角<钝角<平角<周角
1周角=2平角=4直角
二、知识应用
5. 我们学过哪些平面图形?分别说出这些平面图形的特点,并尝试验证。
二、知识应用
二、知识应用
用圆规画圆时,针尖(圆心)决定圆的位置,两脚间的距离(半径)决定圆的大小。
二、知识应用
用圆规画圆时,针尖(圆心)决定圆的位置,两脚间的距离(半径)决定圆的大小。
图形 是否属于轴对称图形 对称轴数目
等腰三角形
等边三角形
长方形
正方形
平行四边形
等腰梯形
圆
是
1
是
3
是
2
是
4
否
无
是
1
是
无数条
二、知识应用
6. 举例说明平面图形的特点在生活中的应用。
三角形的房梁架利用了三角形的稳定性。
推拉闸门利用了平行四边形易变形的特点。
圆形的车轮、井盖等利用了圆的圆心到圆上的距离处处相等的特点。
二、知识应用
7. 一个三角形可能有两个直角吗?与同伴交流你的理由。
一个三角形有三个内角,三个角的和为180°,
1个直角=90°,如果一个三角形内有两个直角,那么这两个角的和为180°,第三个角不存在。
所以一个三角形不可能有两个直角。
三、巩固练习
1. 在下图中找一找,哪些部分可以看作是互相平行的?哪些部分可以看作互相垂直的?
双杠的两条杠杆可以看作互相平行……
两吊环的绳可以看作互相平行,吊环的绳与手臂互相垂直……
人体与单杠呈垂直状态,两条竖杠互相平行,横杠与竖杠互相垂直……
三、巩固练习
2. 按要求作图。
(1)过图中的点A画直线BC的垂线。
量一量,点A到直线BC的距离是多少?
三、巩固练习
(2)在下面的方格图中,画出一个长方形、平行四边形和梯形。
2. 按要求作图。
三、巩固练习
3. 求下面三角形中各角的度数。
∠1=180°-40°-80°
=60°
∠2=180°-90°-30°
=60°
∠3=180°-60°-60°
=60°
三、巩固练习
4. 在能围成三角形的一组线段下面画“√”。(单位:cm)
0.5+1=1.5
1.5<1.8
1+2.5=3.5
3.5>3
√
2+2=4
三角形中,任意两边之和大于第三边。
三、巩固练习
6. 想一想,画一画。
如何画出上面的图形,怎样确定圆心和半径。
四、课堂小结
1. 三角形任意两边之和大于第三边,三个内角
之和等于180°。
2. 平行四边形两组对边平行且相等。
3. 长方形两组对边平行且相等,四个角都是直角。
4. 正方形两组对边平行,四条边都相等,四个角
都是直角。
5. 梯形的一组对边平行。
第2课时 图形的认识(二)
总复习
一、回顾整理
【回顾1】线段、射线、直线
线段
直线上两点间的一段叫作线段,线段有两个端点,可以度量长度。
射线
把线段的一端无限延长,就得到一条射线,射线只有一个端点,它是无限长的,不能度量长度。
直线
把线段的两端无限延长,就得到一条直线,直线没有端点,它是无限长的,不能度量长度。
一、回顾整理
【回顾2】角
角的意义
从一点引出两条射线,就组成一个角。角有一个顶点和两条边。
角的分类及大小关系
角包括锐角、直角、钝角、平角、周角等。
锐角<直角<钝角<平角<周角
1周角=2平角=4直角
一、回顾整理
【回顾3】垂直与平行
两条直线相交成直角时,这两条直线互相垂直。其中一条直线叫作另一条直线的垂线,这两条直线的交点叫作垂足。
在同一平面内,不相交的两条直线叫作平行线。
垂直、垂线与垂足
平行线
二、知识应用
3. 画两条直线,想一想,在什么情况下两条直线互相垂直?在什么
情况下两条直线互相平行?
垂足
两条直线相交
直线会无限延长,两直线也相交。
两直线相交成直角,两直线互相垂直。
两条直线永远不会相交,平行线之间处处相等。
不在同一平面内。平行与垂直的前提是同一平面内。
二、知识应用
同一平面内,不相交的两直线平行。若两直线相交所成角为90°,则两直线垂直。
平行线间的距离处处相等。
二、知识应用
顶点
边
边
角的组成
二、知识应用
4. 写出下面各角的名称,并说出你的理由。
( )
( )
( )
●
⌒
( )
⊙
( )
锐角
直角
钝角
平角
周角
0°<锐角<90°
直角=90°
90°<钝角<180°
平角=180°
周角=360°
锐角<直角<钝角<平角<周角
1周角=2平角=4直角
二、知识应用
5. 我们学过哪些平面图形?分别说出这些平面图形的特点,并尝试验证。
二、知识应用
二、知识应用
用圆规画圆时,针尖(圆心)决定圆的位置,两脚间的距离(半径)决定圆的大小。
二、知识应用
用圆规画圆时,针尖(圆心)决定圆的位置,两脚间的距离(半径)决定圆的大小。
图形 是否属于轴对称图形 对称轴数目
等腰三角形
等边三角形
长方形
正方形
平行四边形
等腰梯形
圆
是
1
是
3
是
2
是
4
否
无
是
1
是
无数条
二、知识应用
6. 举例说明平面图形的特点在生活中的应用。
三角形的房梁架利用了三角形的稳定性。
推拉闸门利用了平行四边形易变形的特点。
圆形的车轮、井盖等利用了圆的圆心到圆上的距离处处相等的特点。
二、知识应用
7. 一个三角形可能有两个直角吗?与同伴交流你的理由。
一个三角形有三个内角,三个角的和为180°,
1个直角=90°,如果一个三角形内有两个直角,那么这两个角的和为180°,第三个角不存在。
所以一个三角形不可能有两个直角。
三、巩固练习
1. 在下图中找一找,哪些部分可以看作是互相平行的?哪些部分可以看作互相垂直的?
双杠的两条杠杆可以看作互相平行……
两吊环的绳可以看作互相平行,吊环的绳与手臂互相垂直……
人体与单杠呈垂直状态,两条竖杠互相平行,横杠与竖杠互相垂直……
三、巩固练习
2. 按要求作图。
(1)过图中的点A画直线BC的垂线。
量一量,点A到直线BC的距离是多少?
三、巩固练习
(2)在下面的方格图中,画出一个长方形、平行四边形和梯形。
2. 按要求作图。
三、巩固练习
3. 求下面三角形中各角的度数。
∠1=180°-40°-80°
=60°
∠2=180°-90°-30°
=60°
∠3=180°-60°-60°
=60°
三、巩固练习
4. 在能围成三角形的一组线段下面画“√”。(单位:cm)
0.5+1=1.5
1.5<1.8
1+2.5=3.5
3.5>3
√
2+2=4
三角形中,任意两边之和大于第三边。
三、巩固练习
6. 想一想,画一画。
如何画出上面的图形,怎样确定圆心和半径。
四、课堂小结
1. 三角形任意两边之和大于第三边,三个内角
之和等于180°。
2. 平行四边形两组对边平行且相等。
3. 长方形两组对边平行且相等,四个角都是直角。
4. 正方形两组对边平行,四条边都相等,四个角
都是直角。
5. 梯形的一组对边平行。
