2021--2022学年人教版八年级数学上册第13章轴对称 13.3等腰三角形复习课教案
文档属性
| 名称 | 2021--2022学年人教版八年级数学上册第13章轴对称 13.3等腰三角形复习课教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 211.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-26 00:00:00 | ||
图片预览



文档简介
《等腰三角形》复习课
学情分析:
八年级的学生已经对等腰三角形的定义、性质、判定等知识有了一定的了解和掌握,具备了一定的逻辑推理能力,也有了小组互助合作的经验,具备了一定的合作交流能力,但碍于基础相对薄弱,缺乏针对性训练,学生很难系统的构建知识体系。本课时是对等腰三角形知识的复习总结,要注重各部分知识之间的纵向联系与横向联系,构建出相对应的知识结构体系达到知识的内化。
教材分析:
①本节内容是新人教版八年级上册第13章《轴对称》中的重点部分,等腰三角形是基本的几何图形之一,在今后的几何学习中有着重要的地位,是构成复杂图形的基本单位,等腰三角形的定理为今后有关几何问题的解决提供了有力的工具.
②对称是几何图形观察和思维的重要思想,也是解决生活中实际问题的常用出发点之一,学好本节知识对加深对称思想的理解有重要意义.
③题中的几何运算,是数形结合的思想的体现和训练,如何在几何中融入代数思想是教学中应重点研究的问题.
教学目标:
①知识目标:熟练掌握等腰三角形、等边三角形的性质和判定,并能运用它来解决实际问题.
②能力目标:通过让学生体会数形结合思想,培养学生勤于思考,善于归纳,积极探索的能力.
③情感目标:通过本节课的学习,让学生感受与人交流、讨论解决问题的快乐,体验成功的喜悦,培养学生学习数学的激情及钻研探索精神.
教学重、难点:
①重点:等腰三角形性质与判定应用.
②难点:等腰三角形性质、判定的具体应用;对图形的观察分析,证明的思路和方法.
教学方法:启发引导、合作探究法、运用数学思想(分类讨论、转化思想)
教学用具:自制一个等腰三角形模型、多媒体
教学过程:
一、考点分析
1、命题方式:对等腰三角形的性质、判定及三角形全等、线段垂直平分线进行综合考查,题型以选择、填空或解答题为主;
2、命题热点:等边三角形的性质的综合运用.
二、知识点梳理
三、基础巩固
判断下列说法是否正确,如果不正确请说明理由
等腰三角形高、中线、角平分线重合( )
一个三角形有两个角分别为80°、20°,则这个三角形是等腰三角形( )
一个三角形的周长为25,两条边长分别为8和9,则这个三角形是等腰三角形( )
等边三角形有且只有一条对称轴( )
有一个角等于60°的等腰三角形是等边三角形( )
选择正确的选项
等腰三角形一个角的度数为50°,则顶角的度数为( )
A、50° B、80° C、65° D、50°或80°
已知等腰△ABC的两边分别为2和3,则等腰△ABC的周长为( )
A、7 B、8 C、6或8 D、7或8
如图,△ABC是等边三角形,DE∥BC,若AB=5,BD=3,则△ADE的周长为( )
A、2 B、6 C、9 D、15
下列条件中,不能得到等边三角形的是( )
有两个内角60°的三角形 B、三边都相等的三角形
有一个角是60°的等腰三角形 D、有两个外角相等的等腰三角形
等腰三角形一腰的高与另一腰的夹角为30°,则顶角的度数为( )
A、60° B、120° C、65°或150° D、60°或120°
四、综合运用
如图,△ABC中,AB=AC,AD=AE,请证明:BE=CD.
4、如图,在△ABC中,AB=AC,AD是BC边上的中线,BE⊥AC于点E,求证:∠CBE=∠BAD.
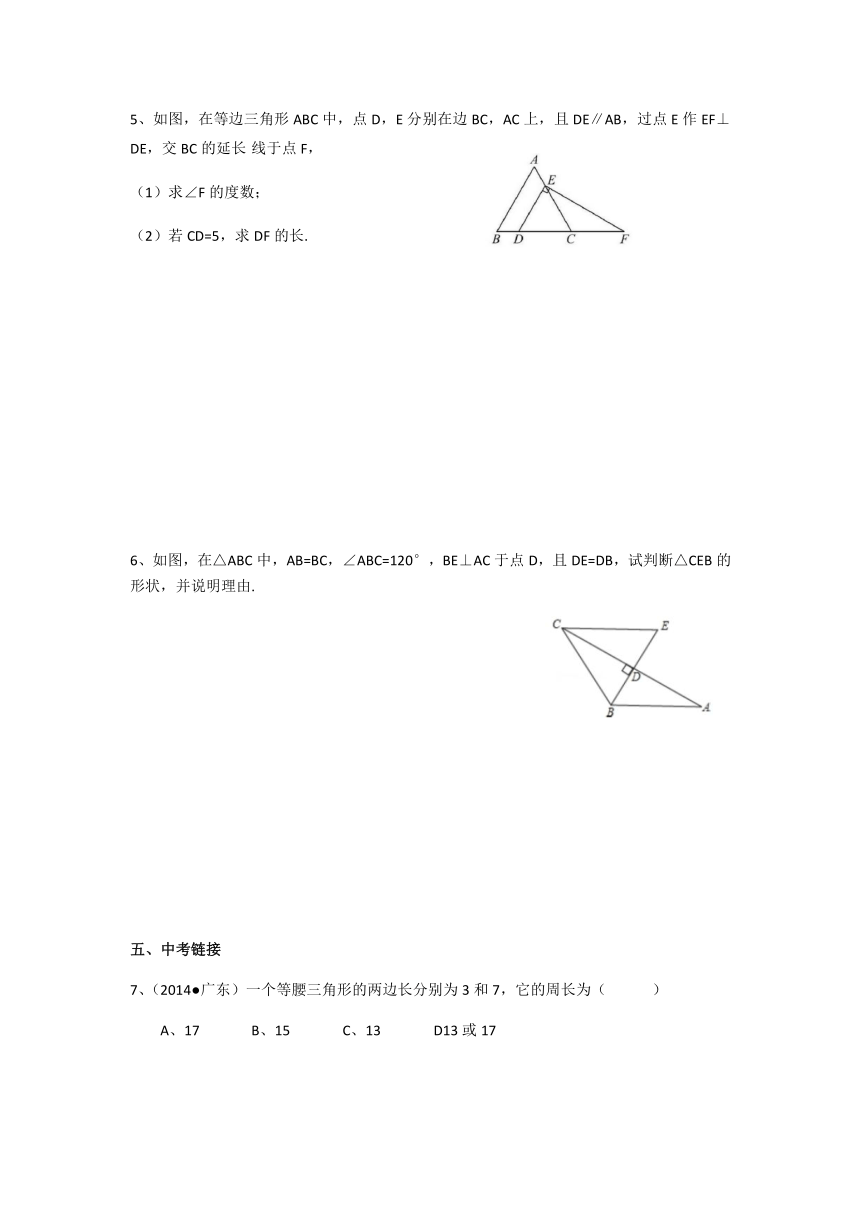
5、如图,在等边三角形ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长 线于点F,
求∠F的度数;
若CD=5,求DF的长.
6、如图,在△ABC中,AB=BC,∠ABC=120°,BE⊥AC于点D,且DE=DB,试判断△CEB的形状,并说明理由.
五、中考链接
7、(2014●广东)一个等腰三角形的两边长分别为3和7,它的周长为( )
A、17 B、15 C、13 D13或17
8、(2020●广东)如图,在△ABC中,点D,E分别是AB,AC边上的点,BD=CE,∠ABE=∠ACD,BE与CD相交 于点F,求证:△ABC是等腰三角形.
(2018●广东)如图,矩形ABCD中,AB>AD,把矩形沿对角线AC所在直线折叠,使点B落在点E处,AE 交CD于点F,连接DE.
求证:△ADE≌△CED;
求证:△DEF是等腰三角形.
课后小测
班级: 姓名: 日期: 得分:
【基础过关】
1、如图,在等腰△ABC中,AB=AC,若∠A=100°,则∠B= .
2、如图,在△ABC中,∠B=∠C,AB=5,则AC的长为 .
3、如图3,在△ABC中,AC=AD=BD,∠DAC=80°,则∠B的度数是( )
A、40° B、35° C、25° D、20°
图3 图4 图5
4、如图4,∠C=90°,AD平分∠BAC交BC于点D,若BC=5cm,BD=3cm,则点D到AB的距离为( )
A、5cm B、3cm C、2cm D、不能确定
5、如图5,等边三角形ABC中,AD⊥BC,垂足为D,点E在线段AD上,∠EBC=45°,则∠ACE的度数为( )
A、15° B、30° C、45° D、60°
【能力提升】
6、如图,△ABC中,D是AC上的一点,且AD=DB=BC,∠DBC=20°,试求∠A的度数.
7、如图,CA=CB,DF=DB,AE=AD,求∠A的度数.
8、如图,在△ABC中,∠ACB=90°,CD是AB边上的高,∠A=30°,求证:AB=4BD.
9、如图,△ABC是等边三角形,∠CBD=90°,BD=BC,连接AD交BC于点E,求∠BAD的度数.
如图,△ABC是等边三角形,BD是AC边上的高,延长BC至E,使CE=CD,连接DE.
∠E等于多少度?
△DBE是什么三角形?为什么?
学情分析:
八年级的学生已经对等腰三角形的定义、性质、判定等知识有了一定的了解和掌握,具备了一定的逻辑推理能力,也有了小组互助合作的经验,具备了一定的合作交流能力,但碍于基础相对薄弱,缺乏针对性训练,学生很难系统的构建知识体系。本课时是对等腰三角形知识的复习总结,要注重各部分知识之间的纵向联系与横向联系,构建出相对应的知识结构体系达到知识的内化。
教材分析:
①本节内容是新人教版八年级上册第13章《轴对称》中的重点部分,等腰三角形是基本的几何图形之一,在今后的几何学习中有着重要的地位,是构成复杂图形的基本单位,等腰三角形的定理为今后有关几何问题的解决提供了有力的工具.
②对称是几何图形观察和思维的重要思想,也是解决生活中实际问题的常用出发点之一,学好本节知识对加深对称思想的理解有重要意义.
③题中的几何运算,是数形结合的思想的体现和训练,如何在几何中融入代数思想是教学中应重点研究的问题.
教学目标:
①知识目标:熟练掌握等腰三角形、等边三角形的性质和判定,并能运用它来解决实际问题.
②能力目标:通过让学生体会数形结合思想,培养学生勤于思考,善于归纳,积极探索的能力.
③情感目标:通过本节课的学习,让学生感受与人交流、讨论解决问题的快乐,体验成功的喜悦,培养学生学习数学的激情及钻研探索精神.
教学重、难点:
①重点:等腰三角形性质与判定应用.
②难点:等腰三角形性质、判定的具体应用;对图形的观察分析,证明的思路和方法.
教学方法:启发引导、合作探究法、运用数学思想(分类讨论、转化思想)
教学用具:自制一个等腰三角形模型、多媒体
教学过程:
一、考点分析
1、命题方式:对等腰三角形的性质、判定及三角形全等、线段垂直平分线进行综合考查,题型以选择、填空或解答题为主;
2、命题热点:等边三角形的性质的综合运用.
二、知识点梳理
三、基础巩固
判断下列说法是否正确,如果不正确请说明理由
等腰三角形高、中线、角平分线重合( )
一个三角形有两个角分别为80°、20°,则这个三角形是等腰三角形( )
一个三角形的周长为25,两条边长分别为8和9,则这个三角形是等腰三角形( )
等边三角形有且只有一条对称轴( )
有一个角等于60°的等腰三角形是等边三角形( )
选择正确的选项
等腰三角形一个角的度数为50°,则顶角的度数为( )
A、50° B、80° C、65° D、50°或80°
已知等腰△ABC的两边分别为2和3,则等腰△ABC的周长为( )
A、7 B、8 C、6或8 D、7或8
如图,△ABC是等边三角形,DE∥BC,若AB=5,BD=3,则△ADE的周长为( )
A、2 B、6 C、9 D、15
下列条件中,不能得到等边三角形的是( )
有两个内角60°的三角形 B、三边都相等的三角形
有一个角是60°的等腰三角形 D、有两个外角相等的等腰三角形
等腰三角形一腰的高与另一腰的夹角为30°,则顶角的度数为( )
A、60° B、120° C、65°或150° D、60°或120°
四、综合运用
如图,△ABC中,AB=AC,AD=AE,请证明:BE=CD.
4、如图,在△ABC中,AB=AC,AD是BC边上的中线,BE⊥AC于点E,求证:∠CBE=∠BAD.
5、如图,在等边三角形ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长 线于点F,
求∠F的度数;
若CD=5,求DF的长.
6、如图,在△ABC中,AB=BC,∠ABC=120°,BE⊥AC于点D,且DE=DB,试判断△CEB的形状,并说明理由.
五、中考链接
7、(2014●广东)一个等腰三角形的两边长分别为3和7,它的周长为( )
A、17 B、15 C、13 D13或17
8、(2020●广东)如图,在△ABC中,点D,E分别是AB,AC边上的点,BD=CE,∠ABE=∠ACD,BE与CD相交 于点F,求证:△ABC是等腰三角形.
(2018●广东)如图,矩形ABCD中,AB>AD,把矩形沿对角线AC所在直线折叠,使点B落在点E处,AE 交CD于点F,连接DE.
求证:△ADE≌△CED;
求证:△DEF是等腰三角形.
课后小测
班级: 姓名: 日期: 得分:
【基础过关】
1、如图,在等腰△ABC中,AB=AC,若∠A=100°,则∠B= .
2、如图,在△ABC中,∠B=∠C,AB=5,则AC的长为 .
3、如图3,在△ABC中,AC=AD=BD,∠DAC=80°,则∠B的度数是( )
A、40° B、35° C、25° D、20°
图3 图4 图5
4、如图4,∠C=90°,AD平分∠BAC交BC于点D,若BC=5cm,BD=3cm,则点D到AB的距离为( )
A、5cm B、3cm C、2cm D、不能确定
5、如图5,等边三角形ABC中,AD⊥BC,垂足为D,点E在线段AD上,∠EBC=45°,则∠ACE的度数为( )
A、15° B、30° C、45° D、60°
【能力提升】
6、如图,△ABC中,D是AC上的一点,且AD=DB=BC,∠DBC=20°,试求∠A的度数.
7、如图,CA=CB,DF=DB,AE=AD,求∠A的度数.
8、如图,在△ABC中,∠ACB=90°,CD是AB边上的高,∠A=30°,求证:AB=4BD.
9、如图,△ABC是等边三角形,∠CBD=90°,BD=BC,连接AD交BC于点E,求∠BAD的度数.
如图,△ABC是等边三角形,BD是AC边上的高,延长BC至E,使CE=CD,连接DE.
∠E等于多少度?
△DBE是什么三角形?为什么?
