两条直线平行与垂直的判定
图片预览










文档简介
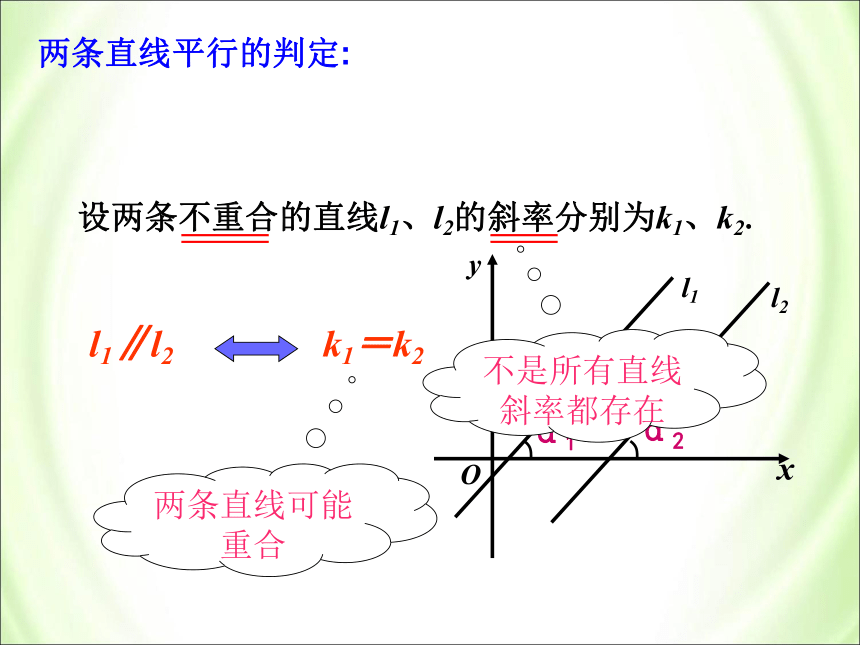
课件30张PPT。3.1 直线的倾斜角与斜率第三章 直线与方程 复习1.直线的倾斜角:2.直线的斜率:3.由直线上两点确定直线的斜率:思考? 在平面直角坐标系下,倾斜角可以表示直线的倾斜程度, 斜率也可以表示直线相对于x轴的倾斜程度。我们能否通过直线斜率来判断两条直线的位置关系?Oyxl1l2α两条直线平行的判定:设两条不重合的直线l1、l2的斜率分别为k1、k2.两条直线可能重合不是所有直线斜率都存在想一想判断下列说法是否正确:(1) 若两条直线的斜率相等,这两条直线一定平行.(2)若两条直线平行,则它们的斜率一定相等.(3)若两条直线平行且倾斜角不是直角,则它们的斜
率一定相等.(4)若两条不重合的直线的斜率都不存在,则它们互
相平行.如果直线L1,L2的斜率为k1,k2.
那么
L1∥L2 ? k1=k2注意:上面的等价是在两直线斜率存在且不重合的前提下才成立的,缺少这个前提,结论并不存立.特殊情况下的两直线平行:
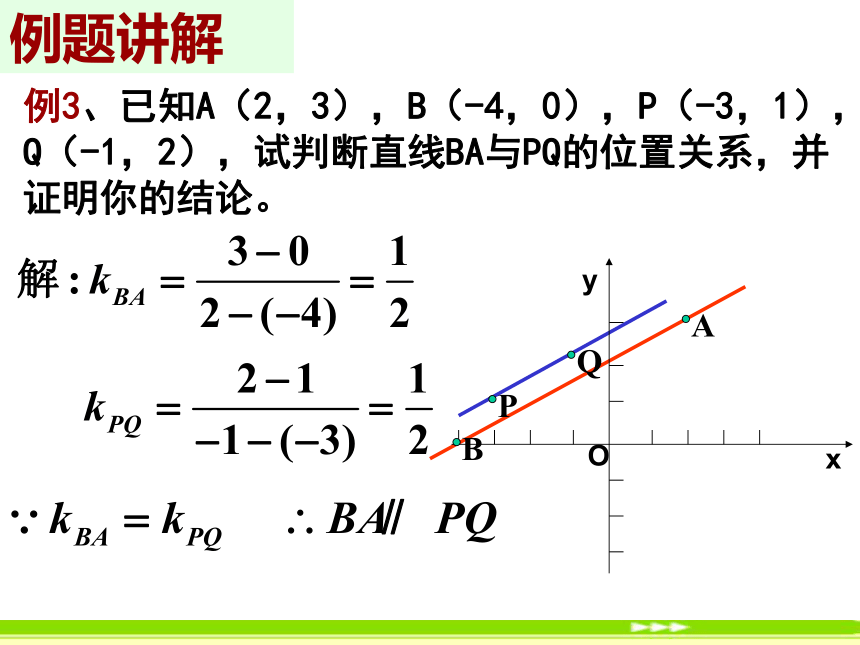
两直线的倾斜角都为90°,互相平行.例题讲解例3、已知A(2,3),B(-4,0),P(-3,1),Q(-1,2),试判断直线BA与PQ的位置关系,并证明你的结论。∥例4 已知四边形ABCD的四个顶点分别为A(0,0),B(2,-1),C(4,2),D(2,3),试判断四边形ABCD的形状,并给出证明。
创新49页两条直线垂直的判定:设两条直线l1、l2的倾斜角分别为α1、α2
( α1,α2≠90°).则α2=α1+90°两条直线l1、l2的斜率分别
为k1、k2,则有只适用于k存在的两条直线想一想判断下列说法是否正确:(2)若两条直线垂直, 则它们的斜率之积一定为-1.(3)若两条直线中,一条没有斜率,另一条的斜率为零,
它们的位置关系也是垂直.若两条直线的斜率之积为-1, 这两条直线一定
垂直.知识点梳理 如果两直线的斜率为k1, k2,那么,这两条直线垂直
的充要条件是k1·k2= -1注意:上面的等价是在两直线斜率存在的前提下才成立的,
缺少这个前提,结论并不存立.特殊情况下的两直线平行与垂直: 当一条直线的倾斜角为900,另一条直线的倾斜角为0°
两直线互相垂直例5、已知A(-6,0),B(3,6),P(0,3) Q(6,-6),判断直线AB与PQ的位置关系。例题讲解例6、已知A(5,-1),B(1,1),C(2,3)三点,试判断△ABC的形状。练习:课本89页 1,2创新50页活页规范训练3.若直线l经过点(a-2,-1)和(-a-2,1),且与经过点(-2,1),斜率为- 的直线垂直,则实数a的值是( ).
A.- B.- C. D.
解析 由于直线l与经过点(-2,1)且斜率为- 的直线垂直,可知a-2≠-a-2.
∵kl= =- ,
∴- · (- )=-1,∴a=- .
答案 A4.直线l1的倾斜角为45°,直线l2过A(-2,-1),B(3,4),则l1与l2的位置关系为________.
解析 ∵直线l1的倾斜角为45°,
∴k1=1.
又∵直线l2过A(-2,-1),B(3,4),
∴k2= =1.
∴k1=k2,∴l1与l2平行或重合.
答案 平行或重合5.直线l1,l2的斜率是方程x2-3x-1=0的两根,则l1与l2的位置关系是________.
解析 ∵l1,l2的斜率是方程x2-3x-1=0的两根,不妨设斜率分别为k1,k2,则k1·k2=-1,∴l1⊥l2.
答案 垂直6.(2012·威海高一检测)已知A(1,0),B(3,2),C(0,4),点D满足AB⊥CD,且AD∥BC,过求点D的坐标.
解 设D(x,y),则kAB= =1,kBC= =- ,kCD= ,kAD= .
因为AB⊥CD,AD∥BC,所以kAB·kCD=-1,kAD=kBC,
所以 ,解得 ,
即D(10,-6). 7.直线l1的斜率为2,l1∥l2,直线l2过点(-1,1)且与y轴交于点P,则P点坐标为( ).
A.(3,0) B.(-3,0)
C.(0,-3) D.(0,3)
解析 设P(0,y),∴k2=y-1,
∵l1∥l2,∴y-1=2,∴y=3,故选D.
答案 D8.若点P(a,b)与Q(b-1,a+1)关于直线l对称,则l的倾斜角为( ).
A.135° B.45° C.30° D.60°
解析 由题意知,PQ⊥l,∵kPQ= =-1,
∴kl=1,即tan α=1,∴α=45°.
答案 B11.已知直线l1经过点A(3,a),B(a-2,-3),直线l2经过点C(2,3),D(-1,a-2),如果l1⊥l2,求a的值.
解 设直线l1,l2的斜率分别为k1,k2.
∵直线l2经过点C(2,3),D(-1,a-2),且2≠-1,∴l2的斜率存在.
当k2=0时,k1不存在,a-2=3,则a=5;
当k2≠0时,即a≠5,此时k1≠0,
由k1·k2=-1,得 · =-1, 解得a=-6.
综上可知,a的值为5或-6.12.(创新拓展)已知在?ABCD中,A(1,2),B(5,0),C(3,4).
(1)求点D的坐标;
解 (1)设D(a,b),由?ABCD,得kAB=kCD,
kAD=kBC,
即 ,解得 ,
∴D(-1,6).12.(创新拓展)已知在?ABCD中,A(1,2),B(5,0),C(3,4).
(2)试判定?ABCD是否为菱形?
∴D(-1,6).
(2)∵kAC= =1,kBD= =-1,
∴kAC·kBD=-1,
∴AC⊥BD.∴?ABCD为菱形.
率一定相等.(4)若两条不重合的直线的斜率都不存在,则它们互
相平行.如果直线L1,L2的斜率为k1,k2.
那么
L1∥L2 ? k1=k2注意:上面的等价是在两直线斜率存在且不重合的前提下才成立的,缺少这个前提,结论并不存立.特殊情况下的两直线平行:
两直线的倾斜角都为90°,互相平行.例题讲解例3、已知A(2,3),B(-4,0),P(-3,1),Q(-1,2),试判断直线BA与PQ的位置关系,并证明你的结论。∥例4 已知四边形ABCD的四个顶点分别为A(0,0),B(2,-1),C(4,2),D(2,3),试判断四边形ABCD的形状,并给出证明。
创新49页两条直线垂直的判定:设两条直线l1、l2的倾斜角分别为α1、α2
( α1,α2≠90°).则α2=α1+90°两条直线l1、l2的斜率分别
为k1、k2,则有只适用于k存在的两条直线想一想判断下列说法是否正确:(2)若两条直线垂直, 则它们的斜率之积一定为-1.(3)若两条直线中,一条没有斜率,另一条的斜率为零,
它们的位置关系也是垂直.若两条直线的斜率之积为-1, 这两条直线一定
垂直.知识点梳理 如果两直线的斜率为k1, k2,那么,这两条直线垂直
的充要条件是k1·k2= -1注意:上面的等价是在两直线斜率存在的前提下才成立的,
缺少这个前提,结论并不存立.特殊情况下的两直线平行与垂直: 当一条直线的倾斜角为900,另一条直线的倾斜角为0°
两直线互相垂直例5、已知A(-6,0),B(3,6),P(0,3) Q(6,-6),判断直线AB与PQ的位置关系。例题讲解例6、已知A(5,-1),B(1,1),C(2,3)三点,试判断△ABC的形状。练习:课本89页 1,2创新50页活页规范训练3.若直线l经过点(a-2,-1)和(-a-2,1),且与经过点(-2,1),斜率为- 的直线垂直,则实数a的值是( ).
A.- B.- C. D.
解析 由于直线l与经过点(-2,1)且斜率为- 的直线垂直,可知a-2≠-a-2.
∵kl= =- ,
∴- · (- )=-1,∴a=- .
答案 A4.直线l1的倾斜角为45°,直线l2过A(-2,-1),B(3,4),则l1与l2的位置关系为________.
解析 ∵直线l1的倾斜角为45°,
∴k1=1.
又∵直线l2过A(-2,-1),B(3,4),
∴k2= =1.
∴k1=k2,∴l1与l2平行或重合.
答案 平行或重合5.直线l1,l2的斜率是方程x2-3x-1=0的两根,则l1与l2的位置关系是________.
解析 ∵l1,l2的斜率是方程x2-3x-1=0的两根,不妨设斜率分别为k1,k2,则k1·k2=-1,∴l1⊥l2.
答案 垂直6.(2012·威海高一检测)已知A(1,0),B(3,2),C(0,4),点D满足AB⊥CD,且AD∥BC,过求点D的坐标.
解 设D(x,y),则kAB= =1,kBC= =- ,kCD= ,kAD= .
因为AB⊥CD,AD∥BC,所以kAB·kCD=-1,kAD=kBC,
所以 ,解得 ,
即D(10,-6). 7.直线l1的斜率为2,l1∥l2,直线l2过点(-1,1)且与y轴交于点P,则P点坐标为( ).
A.(3,0) B.(-3,0)
C.(0,-3) D.(0,3)
解析 设P(0,y),∴k2=y-1,
∵l1∥l2,∴y-1=2,∴y=3,故选D.
答案 D8.若点P(a,b)与Q(b-1,a+1)关于直线l对称,则l的倾斜角为( ).
A.135° B.45° C.30° D.60°
解析 由题意知,PQ⊥l,∵kPQ= =-1,
∴kl=1,即tan α=1,∴α=45°.
答案 B11.已知直线l1经过点A(3,a),B(a-2,-3),直线l2经过点C(2,3),D(-1,a-2),如果l1⊥l2,求a的值.
解 设直线l1,l2的斜率分别为k1,k2.
∵直线l2经过点C(2,3),D(-1,a-2),且2≠-1,∴l2的斜率存在.
当k2=0时,k1不存在,a-2=3,则a=5;
当k2≠0时,即a≠5,此时k1≠0,
由k1·k2=-1,得 · =-1, 解得a=-6.
综上可知,a的值为5或-6.12.(创新拓展)已知在?ABCD中,A(1,2),B(5,0),C(3,4).
(1)求点D的坐标;
解 (1)设D(a,b),由?ABCD,得kAB=kCD,
kAD=kBC,
即 ,解得 ,
∴D(-1,6).12.(创新拓展)已知在?ABCD中,A(1,2),B(5,0),C(3,4).
(2)试判定?ABCD是否为菱形?
∴D(-1,6).
(2)∵kAC= =1,kBD= =-1,
∴kAC·kBD=-1,
∴AC⊥BD.∴?ABCD为菱形.
