广东省雷州市第一中学2013届高三10月实验班摸底测试数学(文)试题
文档属性
| 名称 | 广东省雷州市第一中学2013届高三10月实验班摸底测试数学(文)试题 |  | |
| 格式 | zip | ||
| 文件大小 | 317.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-10-28 15:15:41 | ||
图片预览



文档简介
2012-2013学年度第一学期
雷州市第一中学实验班摸底测试题
(文科数学)
一、选择题:(本大题共8小题,每小题5分,满分50分.在每小题给出的四个选项中,只有一项是符合题目要求的。)
1.定义集合运算:.设集合,,则集合的所有元素之和为( )
A.0 B.6 C.12 D.18
2.的值为( )
A.1 B. C. D.
3.已知向量,,若向量,则( )
A.2 B. C. 8 D.
4.在等差数列中,,表示数列的前项和,则( )
A. B. C. D.
5.已知直线、,平面,则下列命题中:
①.若,,则 ②.若,,则
③.若,,则 ④.若,, ,则
其中,真命题有( )
A.0个 B.1个 C.2个 D.3个
6.成等差数列是成立的( )
A.充分非必要条件 B.必要非充分条件
C.充要条件 D.既不充分也不必要条件
7. 设变量满足约束条件,则的最大值为( )
A. B. C. D.
8.给出计算 的值的一个
程序框图如右图,其中判断框内应填入的条件是( )
A. B. C. D.
9. 如图,已知抛物线的焦点F恰好是双曲线的右焦点,且两条曲线的交点的连线过F,则该双曲线的离心率是( )
A. B. C. D.
10.已知都是定义在上的函数,且满足以下条件:
;②;
③.若,则等于 ( )
A. B. C. D. 2或
二、填空题:(本大题共5小题,每小题5分,满分20分.其中14~15题是选做题,考生只能选做一题,2题全答的,只计算前一题得分).
11. 某班有学生52人,现用系统抽样的方法,抽取一个容量为4的样本,已知座位号分别为6,30,42的同学都在样本中,那么样本中还有一位同学的座位号应该是 .
12.如右图,一个空间几何体的主视图和左视图都是边长为1的正三角形,俯视图是一个圆,那么这个几何体的体积为 .
13. 已知定义域为的函数为奇函数,且满足,当时,,则=
14.(几何证明选讲选做题)如右图,四边形ABCD内接
于⊙,BC是直径,MN切⊙于A,,则 .
15.(坐标系与参数方程选做题)极坐标方程分别为和的两个圆的圆心距为____________。
三、解答题:(本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤.)
16.(本小题满分12分)在△ABC中,角A、B、C所对边分别为a,b,c,已知,且最长边的边长为l.,
求:( 1 )角C的大小; ( 2 )△ABC最短边的长.
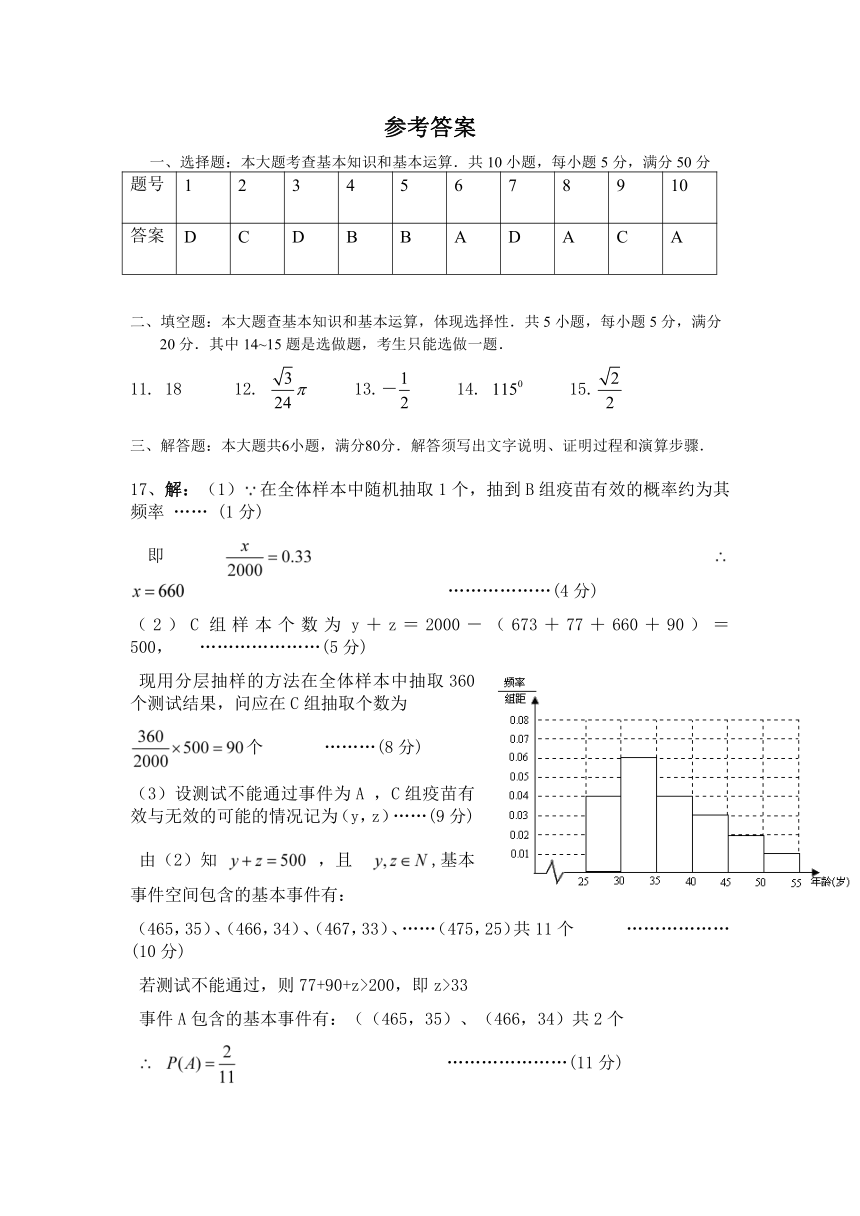
17.(本题满分12分)为预防病毒暴发,某生物技术公司研制出一种新流感疫苗,为测试该疫苗的有效性(若疫苗有效的概率小于90%,则认为测试没有通过),公司选定2000个流感样本分成三组,测试结果如下表:
A组
B组
C组
疫苗有效
673
疫苗无效
77
90
已知在全体样本中随机抽取1个,抽到B组疫苗有效的概率是0.33.
(1)求的值;
(2)现用分层抽样的方法在全体样本中抽取360个测试结果,问应在C组抽取多少个?
(3)已知y465,z25,求不能通过测试的概率.
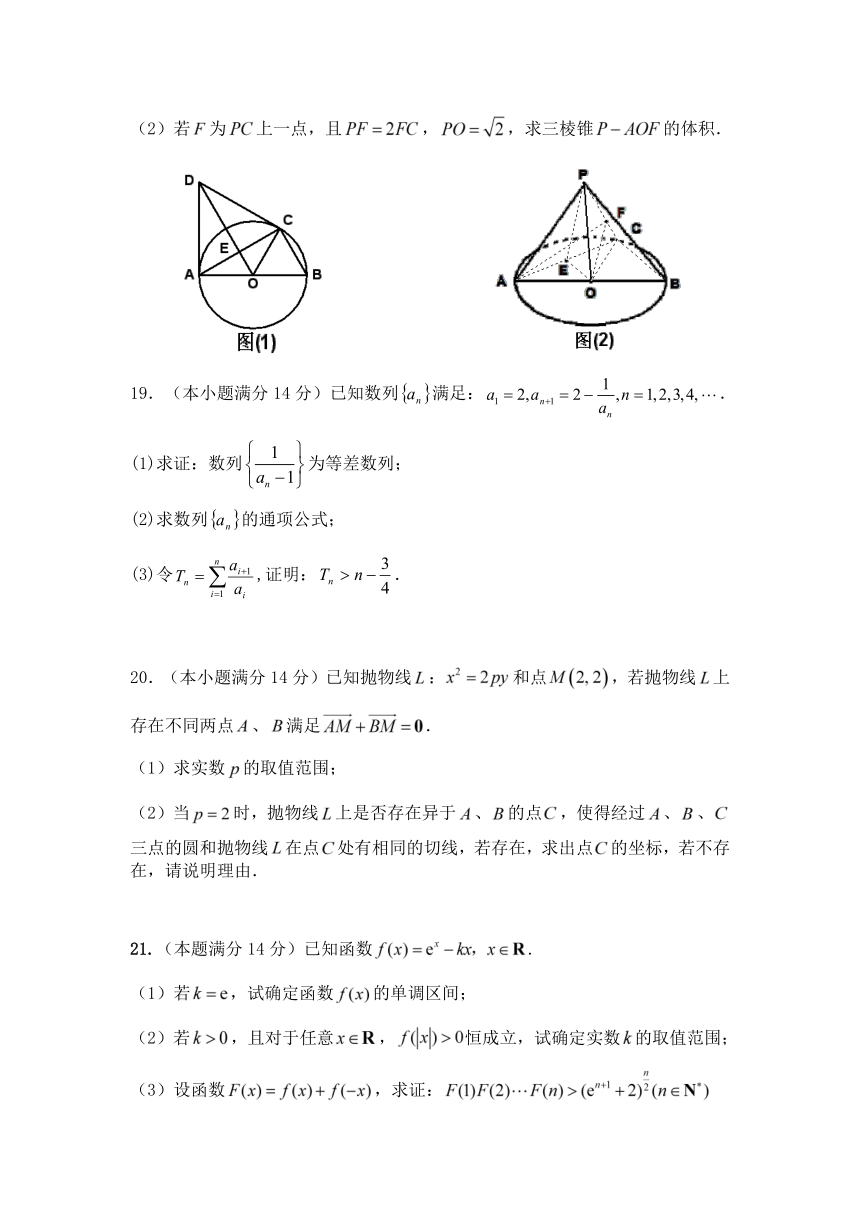
18.(本小题满分14分)如图(1),是直径的圆上一点,为圆O的切线,为切点,为等边三角形,连接交于,以为折痕将翻折到图(2)所示的位置,点P为平面ABC外的点.
(1)求证:异面直线和互相垂直;
(2)若为上一点,且,,求三棱锥的体积.
19.(本小题满分14分)已知数列满足:.
(1)求证:数列为等差数列;
(2)求数列的通项公式;
(3)令,证明:.
20.(本小题满分14分)已知抛物线:和点,若抛物线上存在不同两点、满足.
(1)求实数的取值范围;
(2)当时,抛物线上是否存在异于、的点,使得经过、、三点的圆和抛物线在点处有相同的切线,若存在,求出点的坐标,若不存在,请说明理由.
21.(本题满分14分)已知函数.
(1)若,试确定函数的单调区间;
(2)若,且对于任意,恒成立,试确定实数的取值范围;
(3)设函数,求证:
参考答案
一、选择题:本大题考查基本知识和基本运算.共10小题,每小题5分,满分50分
题号
1
2
3
4
5
6
7
8
9
10
答案
D
C
D
B
B
A
D
A
C
A
二、填空题:本大题查基本知识和基本运算,体现选择性.共5小题,每小题5分,满分20分.其中14~15题是选做题,考生只能选做一题.
11. 18 12. 13. 14. 15.
三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤.
17、解:(1)在全体样本中随机抽取1个,抽到B组疫苗有效的概率约为其频率 …… (1分)
即 ………………(4分)
(2)C组样本个数为y+z=2000-(673+77+660+90)=500, …………………(5分)
现用分层抽样的方法在全体样本中抽取360个测试结果,问应在C组抽取个数为
个 ………(8分)
(3)设测试不能通过事件为A ,C组疫苗有效与无效的可能的情况记为(y,z)……(9分)
由(2)知 ,且 ,基本事件空间包含的基本事件有:
(465,35)、(466,34)、(467,33)、……(475,25)共11个 ……………… (10分)
若测试不能通过,则77+90+z>200,即z>33
事件A包含的基本事件有:((465,35)、(466,34)共2个
…………………(11分)
故不能通过测试的概率为 …………(12分)
18、(1)证明:等边三角形中,为的切线,为切点,
且为中点 (2分)
以为折痕将翻折到图(2)的位置时,
仍有,
平面 (4分)
(5分)
(2)解:,
图(1)中,为的直径,为的切线,为切点,
中,,
, (8分)
,
平面 (10分)
三棱锥的体积
(12分)
为上一点,且,
三棱锥的体积
(14分)
19.(1) 证明:, ===.………3分
数列为等差数列. ………………4分
(2). 由(1)得,为等差数列,公差为1, 首项为.………………6分
(.………………8分 .………9分
(3) , ………10分
. ………11分 .………12分
当时, …………13分
当时, 综上所述:. ………14分
20.(本小题满分14分)
解法1:(1)不妨设A,B,且,
∵,∴.
∴,.…………………4分
∵(),即,
∴,即的取值范围为.…………………6分
(2)当时,由(1)求得.的坐标分别为..
假设抛物线上存在点(且),…………8分
使得经过..三点的圆和抛物线在点处有相同的切线.
设经过..三点的圆的方程为,
则
整理得 . ①…………9分
∵函数的导数为,
∴抛物线在点处的切线的斜率为,
∴经过..三点的圆在点处的切线斜率为.………10分
∵,∴直线的斜率存在.
∵圆心的坐标为,
∴,
即. ②…………………12分
∵,由①.②消去,得.
即.
∵,∴.
故满足题设的点存在,其坐标为.…………………14分
解法2:(1)设,两点的坐标为,且。
∵,可得为的中点,
即.…………………2分
显然直线与轴不垂直,
设直线的方程为,
即,…………………3分
将代入中,
得. …………………4分
∴ ∴.
故的取值范围为. …………………6分
(2)当时,由(1)求得,的坐标分别为.
假设抛物线上存在点(且),
使得经过..三点的圆和抛物线在点处有相同的切线.
设圆的圆心坐标为,
∵ ∴即 …………………8分
解得 …………………10分
∵抛物线在点处切线的斜率为,
而,且该切线与垂直,∴.
即. …………………12分
将,代入上式,
得.
即.∵且,∴.
故满足题设的点存在,其坐标为 . …………………14分
21.解:(1)由得,所以.
由得,故的单调递增区间是,
由得,故的单调递减区间是.……………4分
(2)由可知是偶函数.
于是对任意成立等价于对任意成立.
由得. ……………………………………6分
①当时,.
此时在上单调递增.
故,符合题意. ……………………………………8分
②当时,.
当变化时的变化情况如下表:
单调递减
极小值
单调递增
由此可得,在上,.
依题意,,又.
综合①,②得,实数的取值范围是.………………………10分
【(方法二)由对任意成立等价于恒成立
当,恒成立,则,又,所以此时………6分
当,恒成立,则,令,则,……7分
易知为上偶函数,考察,,,
当时,,当时,,
所以当时,,所以……………………………9分
综上 …………………………………………………………10分】
(3),
,
…………………………………………………………11分
,
……………………………………12分
由此得, ………………………………………13分
故. …………………………14分
雷州市第一中学实验班摸底测试题
(文科数学)
一、选择题:(本大题共8小题,每小题5分,满分50分.在每小题给出的四个选项中,只有一项是符合题目要求的。)
1.定义集合运算:.设集合,,则集合的所有元素之和为( )
A.0 B.6 C.12 D.18
2.的值为( )
A.1 B. C. D.
3.已知向量,,若向量,则( )
A.2 B. C. 8 D.
4.在等差数列中,,表示数列的前项和,则( )
A. B. C. D.
5.已知直线、,平面,则下列命题中:
①.若,,则 ②.若,,则
③.若,,则 ④.若,, ,则
其中,真命题有( )
A.0个 B.1个 C.2个 D.3个
6.成等差数列是成立的( )
A.充分非必要条件 B.必要非充分条件
C.充要条件 D.既不充分也不必要条件
7. 设变量满足约束条件,则的最大值为( )
A. B. C. D.
8.给出计算 的值的一个
程序框图如右图,其中判断框内应填入的条件是( )
A. B. C. D.
9. 如图,已知抛物线的焦点F恰好是双曲线的右焦点,且两条曲线的交点的连线过F,则该双曲线的离心率是( )
A. B. C. D.
10.已知都是定义在上的函数,且满足以下条件:
;②;
③.若,则等于 ( )
A. B. C. D. 2或
二、填空题:(本大题共5小题,每小题5分,满分20分.其中14~15题是选做题,考生只能选做一题,2题全答的,只计算前一题得分).
11. 某班有学生52人,现用系统抽样的方法,抽取一个容量为4的样本,已知座位号分别为6,30,42的同学都在样本中,那么样本中还有一位同学的座位号应该是 .
12.如右图,一个空间几何体的主视图和左视图都是边长为1的正三角形,俯视图是一个圆,那么这个几何体的体积为 .
13. 已知定义域为的函数为奇函数,且满足,当时,,则=
14.(几何证明选讲选做题)如右图,四边形ABCD内接
于⊙,BC是直径,MN切⊙于A,,则 .
15.(坐标系与参数方程选做题)极坐标方程分别为和的两个圆的圆心距为____________。
三、解答题:(本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤.)
16.(本小题满分12分)在△ABC中,角A、B、C所对边分别为a,b,c,已知,且最长边的边长为l.,
求:( 1 )角C的大小; ( 2 )△ABC最短边的长.
17.(本题满分12分)为预防病毒暴发,某生物技术公司研制出一种新流感疫苗,为测试该疫苗的有效性(若疫苗有效的概率小于90%,则认为测试没有通过),公司选定2000个流感样本分成三组,测试结果如下表:
A组
B组
C组
疫苗有效
673
疫苗无效
77
90
已知在全体样本中随机抽取1个,抽到B组疫苗有效的概率是0.33.
(1)求的值;
(2)现用分层抽样的方法在全体样本中抽取360个测试结果,问应在C组抽取多少个?
(3)已知y465,z25,求不能通过测试的概率.
18.(本小题满分14分)如图(1),是直径的圆上一点,为圆O的切线,为切点,为等边三角形,连接交于,以为折痕将翻折到图(2)所示的位置,点P为平面ABC外的点.
(1)求证:异面直线和互相垂直;
(2)若为上一点,且,,求三棱锥的体积.
19.(本小题满分14分)已知数列满足:.
(1)求证:数列为等差数列;
(2)求数列的通项公式;
(3)令,证明:.
20.(本小题满分14分)已知抛物线:和点,若抛物线上存在不同两点、满足.
(1)求实数的取值范围;
(2)当时,抛物线上是否存在异于、的点,使得经过、、三点的圆和抛物线在点处有相同的切线,若存在,求出点的坐标,若不存在,请说明理由.
21.(本题满分14分)已知函数.
(1)若,试确定函数的单调区间;
(2)若,且对于任意,恒成立,试确定实数的取值范围;
(3)设函数,求证:
参考答案
一、选择题:本大题考查基本知识和基本运算.共10小题,每小题5分,满分50分
题号
1
2
3
4
5
6
7
8
9
10
答案
D
C
D
B
B
A
D
A
C
A
二、填空题:本大题查基本知识和基本运算,体现选择性.共5小题,每小题5分,满分20分.其中14~15题是选做题,考生只能选做一题.
11. 18 12. 13. 14. 15.
三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤.
17、解:(1)在全体样本中随机抽取1个,抽到B组疫苗有效的概率约为其频率 …… (1分)
即 ………………(4分)
(2)C组样本个数为y+z=2000-(673+77+660+90)=500, …………………(5分)
现用分层抽样的方法在全体样本中抽取360个测试结果,问应在C组抽取个数为
个 ………(8分)
(3)设测试不能通过事件为A ,C组疫苗有效与无效的可能的情况记为(y,z)……(9分)
由(2)知 ,且 ,基本事件空间包含的基本事件有:
(465,35)、(466,34)、(467,33)、……(475,25)共11个 ……………… (10分)
若测试不能通过,则77+90+z>200,即z>33
事件A包含的基本事件有:((465,35)、(466,34)共2个
…………………(11分)
故不能通过测试的概率为 …………(12分)
18、(1)证明:等边三角形中,为的切线,为切点,
且为中点 (2分)
以为折痕将翻折到图(2)的位置时,
仍有,
平面 (4分)
(5分)
(2)解:,
图(1)中,为的直径,为的切线,为切点,
中,,
, (8分)
,
平面 (10分)
三棱锥的体积
(12分)
为上一点,且,
三棱锥的体积
(14分)
19.(1) 证明:, ===.………3分
数列为等差数列. ………………4分
(2). 由(1)得,为等差数列,公差为1, 首项为.………………6分
(.………………8分 .………9分
(3) , ………10分
. ………11分 .………12分
当时, …………13分
当时, 综上所述:. ………14分
20.(本小题满分14分)
解法1:(1)不妨设A,B,且,
∵,∴.
∴,.…………………4分
∵(),即,
∴,即的取值范围为.…………………6分
(2)当时,由(1)求得.的坐标分别为..
假设抛物线上存在点(且),…………8分
使得经过..三点的圆和抛物线在点处有相同的切线.
设经过..三点的圆的方程为,
则
整理得 . ①…………9分
∵函数的导数为,
∴抛物线在点处的切线的斜率为,
∴经过..三点的圆在点处的切线斜率为.………10分
∵,∴直线的斜率存在.
∵圆心的坐标为,
∴,
即. ②…………………12分
∵,由①.②消去,得.
即.
∵,∴.
故满足题设的点存在,其坐标为.…………………14分
解法2:(1)设,两点的坐标为,且。
∵,可得为的中点,
即.…………………2分
显然直线与轴不垂直,
设直线的方程为,
即,…………………3分
将代入中,
得. …………………4分
∴ ∴.
故的取值范围为. …………………6分
(2)当时,由(1)求得,的坐标分别为.
假设抛物线上存在点(且),
使得经过..三点的圆和抛物线在点处有相同的切线.
设圆的圆心坐标为,
∵ ∴即 …………………8分
解得 …………………10分
∵抛物线在点处切线的斜率为,
而,且该切线与垂直,∴.
即. …………………12分
将,代入上式,
得.
即.∵且,∴.
故满足题设的点存在,其坐标为 . …………………14分
21.解:(1)由得,所以.
由得,故的单调递增区间是,
由得,故的单调递减区间是.……………4分
(2)由可知是偶函数.
于是对任意成立等价于对任意成立.
由得. ……………………………………6分
①当时,.
此时在上单调递增.
故,符合题意. ……………………………………8分
②当时,.
当变化时的变化情况如下表:
单调递减
极小值
单调递增
由此可得,在上,.
依题意,,又.
综合①,②得,实数的取值范围是.………………………10分
【(方法二)由对任意成立等价于恒成立
当,恒成立,则,又,所以此时………6分
当,恒成立,则,令,则,……7分
易知为上偶函数,考察,,,
当时,,当时,,
所以当时,,所以……………………………9分
综上 …………………………………………………………10分】
(3),
,
…………………………………………………………11分
,
……………………………………12分
由此得, ………………………………………13分
故. …………………………14分
同课章节目录
