二次函数《实践与探索》课件
图片预览





文档简介
课件16张PPT。
§27.3实践与探索
海口四中 林利待定系数法求二次函数关系式常用的几种方法
一般式:顶点式:交点式:y=a(x-x1)(x-x2)(a≠0)x1,x2为函数图像与x轴交点的横坐标也称为三点式1、求下列二次函数的最大值或最小值:
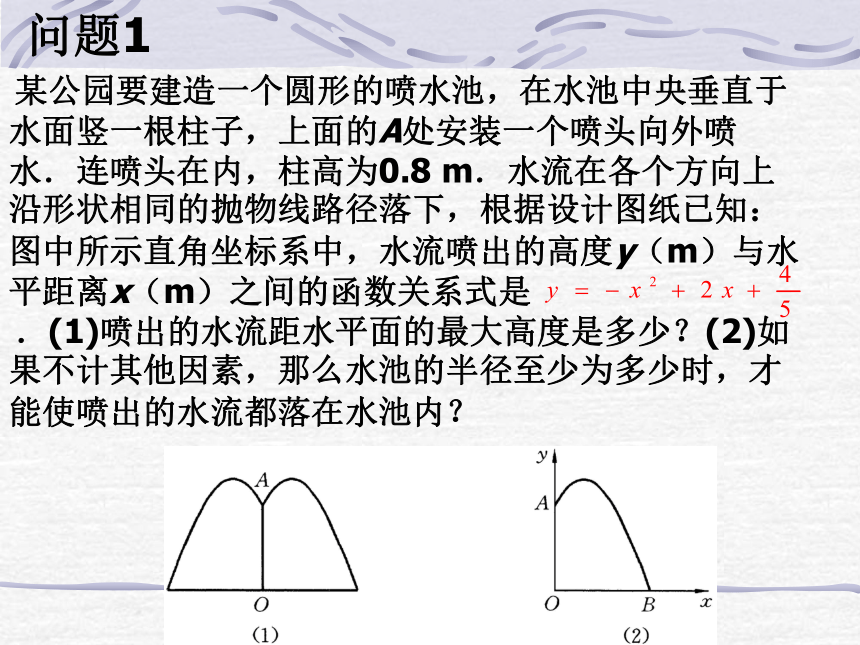
⑴ y=-x2+2x+8; ⑵ y=x2+4x(1)最大,9(2)最小,-4求最大值或最小值需要将二次函数变形为顶点式:问题1 某公园要建造一个圆形的喷水池,在水池中央垂直于水面竖一根柱子,上面的A处安装一个喷头向外喷水.连喷头在内,柱高为0.8 m.水流在各个方向上沿形状相同的抛物线路径落下,根据设计图纸已知:图中所示直角坐标系中,水流喷出的高度y(m)与水平距离x(m)之间的函数关系式是
.(1)喷出的水流距水平面的最大高度是多少?(2)如果不计其他因素,那么水池的半径至少为多少时,才能使喷出的水流都落在水池内?
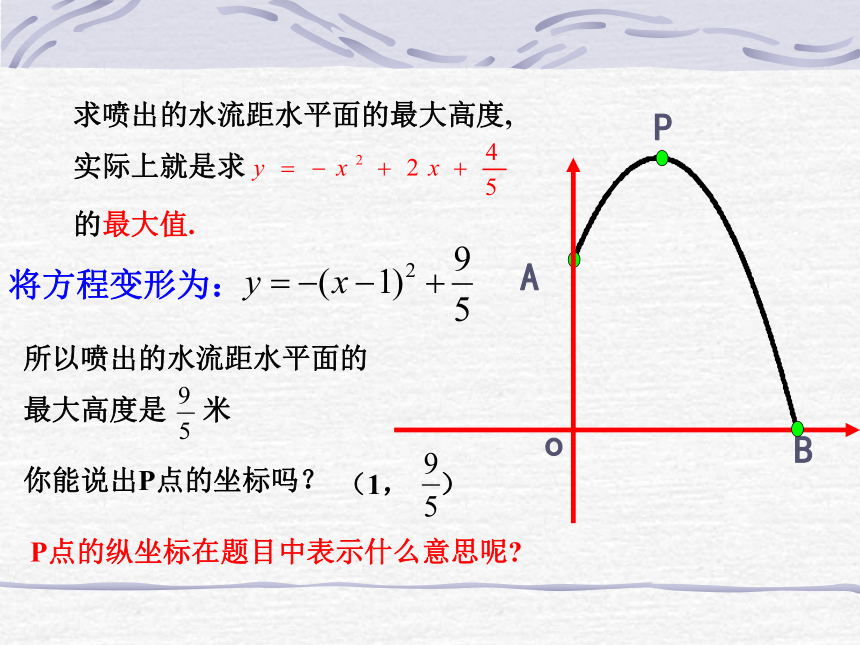
你能说出P点的坐标吗?P点的纵坐标在题目中表示什么意思呢?思考: B点的横坐标和水池的半径有什么样的关系呢?水池的半径最小应等于B点的横坐标。∴水池最小半径为2.34mB点的横坐标在题目中表示什么意思呢?一个涵洞成抛物线形,xyO 一个涵洞成抛物线形,它的截面如图所示,现测得,
当水面宽AB=2米,涵洞顶点O与水面的距离为3米,
以O为原点,AB的中垂线为y轴,建立直角坐标系,1.直接写出A,B,O的坐标
2.求出抛物线的函数关系式3A( ) B( ) O( )问题2y=-3x21设此函数关系式为y=ax2
容易得出此函数的关系式为: -1 , -30 , 01 , -3 一个涵洞成抛物线形,它的截面如图所示,现测得,
当水面宽AB=2米,涵洞顶点与水面的距离为3米,
以O为原点,AB的中垂线为y轴,建立直角坐标系,3.离开水面1.5米处,涵洞宽ED是多少
1.53-1.5OF=1.5→求D点的纵坐标由抛物线的对称性得ED=2FD求D点的横坐标yD=-1.5-1.5= -3x2解方程y= -3x2所以FD=0.71, ED=1.42(m)小船的高为1.3m,宽为1米,能通过这个涵洞吗?一个涵洞成抛物线形,它的截面如图所示,现测得,
当水面宽AB=2米,涵洞顶点D与水面的距离为3米,如何建立适当的直角坐标系?
探索二若水面上涨1米,则此时的水面宽MN为多少? 以AB的中点为原点.O建立直角坐标系方法不一样,但求出的实际宽度是一样的AB哪一种坐标系比较简单?以AB为x轴,A为原点
以抛物线的顶点为原点1.如图,有一个横截面为抛物线的水泥门洞,门洞的高度为8m,门洞内的地面宽度AB=4m,两侧距地面6m高处C,D各有一盏灯,求两灯CD的水平距离?如何建立恰当的直角坐标系呢?xyOFEDCBA8426要求CD的水平距离,只需求 D点的
横坐标.要求D点的横坐标,需先求此函数
关系式和D点的纵坐标?你会求吗?试试看,你一定行!方法步骤:
①建立恰当直角坐标系;
②确定题目中点的坐标.
③求出抛物线的解析式;
④利用图象的性质解决实际问题.课本P27页第二题谢谢再见!
§27.3实践与探索
海口四中 林利待定系数法求二次函数关系式常用的几种方法
一般式:顶点式:交点式:y=a(x-x1)(x-x2)(a≠0)x1,x2为函数图像与x轴交点的横坐标也称为三点式1、求下列二次函数的最大值或最小值:
⑴ y=-x2+2x+8; ⑵ y=x2+4x(1)最大,9(2)最小,-4求最大值或最小值需要将二次函数变形为顶点式:问题1 某公园要建造一个圆形的喷水池,在水池中央垂直于水面竖一根柱子,上面的A处安装一个喷头向外喷水.连喷头在内,柱高为0.8 m.水流在各个方向上沿形状相同的抛物线路径落下,根据设计图纸已知:图中所示直角坐标系中,水流喷出的高度y(m)与水平距离x(m)之间的函数关系式是
.(1)喷出的水流距水平面的最大高度是多少?(2)如果不计其他因素,那么水池的半径至少为多少时,才能使喷出的水流都落在水池内?
你能说出P点的坐标吗?P点的纵坐标在题目中表示什么意思呢?思考: B点的横坐标和水池的半径有什么样的关系呢?水池的半径最小应等于B点的横坐标。∴水池最小半径为2.34mB点的横坐标在题目中表示什么意思呢?一个涵洞成抛物线形,xyO 一个涵洞成抛物线形,它的截面如图所示,现测得,
当水面宽AB=2米,涵洞顶点O与水面的距离为3米,
以O为原点,AB的中垂线为y轴,建立直角坐标系,1.直接写出A,B,O的坐标
2.求出抛物线的函数关系式3A( ) B( ) O( )问题2y=-3x21设此函数关系式为y=ax2
容易得出此函数的关系式为: -1 , -30 , 01 , -3 一个涵洞成抛物线形,它的截面如图所示,现测得,
当水面宽AB=2米,涵洞顶点与水面的距离为3米,
以O为原点,AB的中垂线为y轴,建立直角坐标系,3.离开水面1.5米处,涵洞宽ED是多少
1.53-1.5OF=1.5→求D点的纵坐标由抛物线的对称性得ED=2FD求D点的横坐标yD=-1.5-1.5= -3x2解方程y= -3x2所以FD=0.71, ED=1.42(m)小船的高为1.3m,宽为1米,能通过这个涵洞吗?一个涵洞成抛物线形,它的截面如图所示,现测得,
当水面宽AB=2米,涵洞顶点D与水面的距离为3米,如何建立适当的直角坐标系?
探索二若水面上涨1米,则此时的水面宽MN为多少? 以AB的中点为原点.O建立直角坐标系方法不一样,但求出的实际宽度是一样的AB哪一种坐标系比较简单?以AB为x轴,A为原点
以抛物线的顶点为原点1.如图,有一个横截面为抛物线的水泥门洞,门洞的高度为8m,门洞内的地面宽度AB=4m,两侧距地面6m高处C,D各有一盏灯,求两灯CD的水平距离?如何建立恰当的直角坐标系呢?xyOFEDCBA8426要求CD的水平距离,只需求 D点的
横坐标.要求D点的横坐标,需先求此函数
关系式和D点的纵坐标?你会求吗?试试看,你一定行!方法步骤:
①建立恰当直角坐标系;
②确定题目中点的坐标.
③求出抛物线的解析式;
④利用图象的性质解决实际问题.课本P27页第二题谢谢再见!
