1.2.2 二进制与数制转换 课件-2021-2022学年高中信息技术人教版必修1(28张PPT)
文档属性
| 名称 | 1.2.2 二进制与数制转换 课件-2021-2022学年高中信息技术人教版必修1(28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 491.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 中图版(2019) | ||
| 科目 | 信息技术(信息科技) | ||
| 更新时间 | 2021-12-26 00:00:00 | ||
图片预览








文档简介
(共29张PPT)
1+1=
10
逻辑代数的产生
1849年英国数学家乔治.布尔(George Boole)首先提出,用来描述客观事务逻辑关系的数学方法——称为布尔代数。
后来被广泛用于开关电路和数字逻辑电路的分析与设计,所以也称为开关代数或逻辑代数。
逻辑代数的产生
逻辑代数中用字母表示变量——逻辑变量,每个逻辑变量的取值只有两种可能——0和1。它们也是逻辑代数中仅有的两个常数。0和1只表示两种不同的逻辑状态,不表示数量大小。
日常生活中,我们经常会使用各种数字,如最新一部苹果iPhone 5S手机淘宝不同卖家的价格分别为5288.00元、4998.00元、4999.00元等。这些数都是十进制数。
在实际应用中,还使用其他的计数制,如三双鞋(两只鞋为一双)、两周实习(七天为一周)、4打信封(十二个信封为一打)、半斤八两(一斤十六两)、三天(72小时)、一刻钟(15分)、二小时(120分)等等。
这种逢几进一的计数法,称为进位计数制。简称“数制”或“进制”。
在实际应用中,还尝过哪些计数制?
数制系统
常用的数制系统
生活中:十进制(逢十进一)、六十进制(逢六十进一)
计算机:二进制(逢二进一)、八进制、十进制、十六进制
1. 数制的概念
数制是用一组固定的数码(数字和符号)和一套统一的规则(逢N进一)来表示数目的方法。
数位:数码所在的位置叫做数位。
基数:每个数位上可以使用的数码的个数叫做这种计数制的基数。
位权:
是一个与数字位置有关的常数,位权=
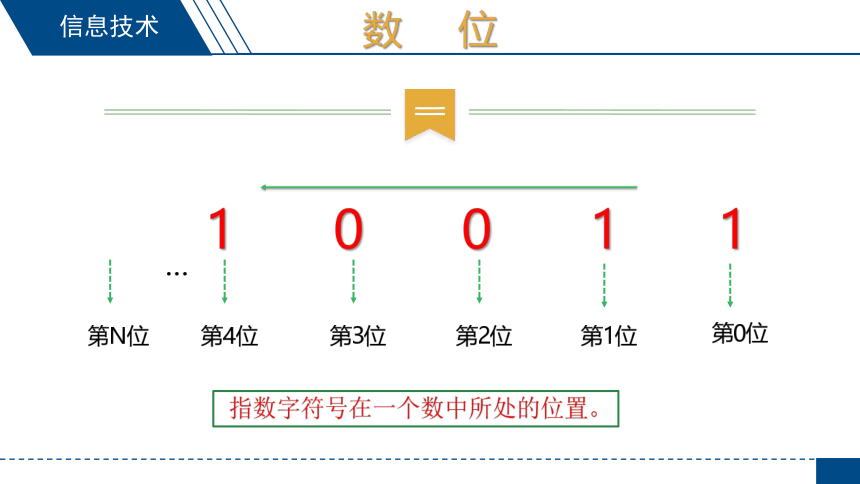
数 位
10011
第0位
第1位
第2位
第3位
第4位
第N位
…
指数字符号在一个数中所处的位置。
基 数
十进制
10
二进制
2
N进制
n
…
…
指在某种进位计数制中,数位上所能使用的数字符号的个数。
权 值
数 位
权 值
10011
第0位
第1位
第2位
第3位
第4位
第N位
…
一个数字处在不同的位置所代表的值,表示为基数的若干次幂。
进位制 二进制 八进制 十进制 十六进制
规则 逢二进一 逢八进一 逢十进一 逢十六进一
基数 R=2 R=8 R=10 R=16
数码 0,1 0,1,2,…,7 0,1,2,…,9 0,1,..,9,A,..,F
权 2i 8i 10i 16i
形式表示 B或( )2 O或( )8 D或( )10 H或( )16
十进制
R进制
除R取余法
二进制
八进制
十六进制
按权展开求和
数的进制——八进制转十进制
(与二进制和十进制转换方法相同)
八进制每个数位乘上对应的权值,最后相加。
(126) 8=( )10
(126)8=1*82+2*81+6*80
=64+16+6
=(86)10
数的进制——十六进制转十进制
(与二进制和十进制转换方法相同)
(D2)16 = 13 × 161 + 2 × 160 = 208 + 2 = (210)10
十六进制每个数位乘上对应的权值,最后相加。
(2A)16=( )10
42
(D2)16 = ( )10
方法:分段法----三位分段
步骤:向左:三位一段,不足三位,左补0
将每段中的三位二进制数转化为一位八进制数
1.3.2
不同进制之间的转换
1.3 计算机中信息的表示方法
二进制数转换为八进制数
例:111 010 001
7
2
1
(1)、一位数转化为三位数;
(2)、不足三位应左补0.
1.3.2
1.3 计算机中信息的表示方法
八进制转换为二进制
例:6 4 2
110
100
010
(1)、一位数转化为四位数;
(2)、不足四位应左补0.
1.3.2
1.3 计算机中信息的表示方法
十六进制转换为二进制
例:C791
0111
1100
0001
1001
数的进制——四则运算
进制规则:
十进制采用逢10进1
如:17+6=23
二进制采用逢2进1
如:(1011)2+(101)2= (10000)2
1.(100110)2=( )10
4.(73)10=( )2
5.(132)10=( )8
6.(321)10=( )16
3.(11E)16 =( )10
2.(77)8 =( )10
7.(11001101101)2=( )8
8.(110011100110)2=( )16
38
63
204
1001001
286
141
3155
CE6
课堂例题
课堂例题
9.(77)8=( )2
10.(AD7)16=( )2
111111
101011010111
11.(25473)8=( )16
2B3B
12.(E1DA)16=( )8
160732
23.(1001101101)2=( )8
1155
1+1=
10
逻辑代数的产生
1849年英国数学家乔治.布尔(George Boole)首先提出,用来描述客观事务逻辑关系的数学方法——称为布尔代数。
后来被广泛用于开关电路和数字逻辑电路的分析与设计,所以也称为开关代数或逻辑代数。
逻辑代数的产生
逻辑代数中用字母表示变量——逻辑变量,每个逻辑变量的取值只有两种可能——0和1。它们也是逻辑代数中仅有的两个常数。0和1只表示两种不同的逻辑状态,不表示数量大小。
日常生活中,我们经常会使用各种数字,如最新一部苹果iPhone 5S手机淘宝不同卖家的价格分别为5288.00元、4998.00元、4999.00元等。这些数都是十进制数。
在实际应用中,还使用其他的计数制,如三双鞋(两只鞋为一双)、两周实习(七天为一周)、4打信封(十二个信封为一打)、半斤八两(一斤十六两)、三天(72小时)、一刻钟(15分)、二小时(120分)等等。
这种逢几进一的计数法,称为进位计数制。简称“数制”或“进制”。
在实际应用中,还尝过哪些计数制?
数制系统
常用的数制系统
生活中:十进制(逢十进一)、六十进制(逢六十进一)
计算机:二进制(逢二进一)、八进制、十进制、十六进制
1. 数制的概念
数制是用一组固定的数码(数字和符号)和一套统一的规则(逢N进一)来表示数目的方法。
数位:数码所在的位置叫做数位。
基数:每个数位上可以使用的数码的个数叫做这种计数制的基数。
位权:
是一个与数字位置有关的常数,位权=
数 位
10011
第0位
第1位
第2位
第3位
第4位
第N位
…
指数字符号在一个数中所处的位置。
基 数
十进制
10
二进制
2
N进制
n
…
…
指在某种进位计数制中,数位上所能使用的数字符号的个数。
权 值
数 位
权 值
10011
第0位
第1位
第2位
第3位
第4位
第N位
…
一个数字处在不同的位置所代表的值,表示为基数的若干次幂。
进位制 二进制 八进制 十进制 十六进制
规则 逢二进一 逢八进一 逢十进一 逢十六进一
基数 R=2 R=8 R=10 R=16
数码 0,1 0,1,2,…,7 0,1,2,…,9 0,1,..,9,A,..,F
权 2i 8i 10i 16i
形式表示 B或( )2 O或( )8 D或( )10 H或( )16
十进制
R进制
除R取余法
二进制
八进制
十六进制
按权展开求和
数的进制——八进制转十进制
(与二进制和十进制转换方法相同)
八进制每个数位乘上对应的权值,最后相加。
(126) 8=( )10
(126)8=1*82+2*81+6*80
=64+16+6
=(86)10
数的进制——十六进制转十进制
(与二进制和十进制转换方法相同)
(D2)16 = 13 × 161 + 2 × 160 = 208 + 2 = (210)10
十六进制每个数位乘上对应的权值,最后相加。
(2A)16=( )10
42
(D2)16 = ( )10
方法:分段法----三位分段
步骤:向左:三位一段,不足三位,左补0
将每段中的三位二进制数转化为一位八进制数
1.3.2
不同进制之间的转换
1.3 计算机中信息的表示方法
二进制数转换为八进制数
例:111 010 001
7
2
1
(1)、一位数转化为三位数;
(2)、不足三位应左补0.
1.3.2
1.3 计算机中信息的表示方法
八进制转换为二进制
例:6 4 2
110
100
010
(1)、一位数转化为四位数;
(2)、不足四位应左补0.
1.3.2
1.3 计算机中信息的表示方法
十六进制转换为二进制
例:C791
0111
1100
0001
1001
数的进制——四则运算
进制规则:
十进制采用逢10进1
如:17+6=23
二进制采用逢2进1
如:(1011)2+(101)2= (10000)2
1.(100110)2=( )10
4.(73)10=( )2
5.(132)10=( )8
6.(321)10=( )16
3.(11E)16 =( )10
2.(77)8 =( )10
7.(11001101101)2=( )8
8.(110011100110)2=( )16
38
63
204
1001001
286
141
3155
CE6
课堂例题
课堂例题
9.(77)8=( )2
10.(AD7)16=( )2
111111
101011010111
11.(25473)8=( )16
2B3B
12.(E1DA)16=( )8
160732
23.(1001101101)2=( )8
1155
同课章节目录
- 第1章 认识数据与大数据
- 主题学习项目:体质数据促健康
- 1.1 数据、信息与知识
- 1.2 数字化与编码
- 1.3 数据科学与大数据
- 第2章 算法与程序实现
- 主题学习项目:编程控灯利出行
- 2.1 解决问题的一般过程和用计算机解决问题
- 2.2 算法的概念及描述
- 2.3 程序设计基本知识
- 2.4 常见算法的程序实现
- 第3章 数据处理与应用
- 主题学习项目:用水分析助决策
- 3.1 数据处理的一般过程
- 3.2 数据采集与整理
- 3.3 数据分析与可视化
- 3.4 数据分析报告与应用
- 第4章 走进智能时代
- 主题学习项目:智能交互益拓展
- 4.1 认识人工智能
- 4.2 利用智能工具解决问题
- 4.3 人工智能的应用与影响
