北师大版 五年级数学下册1.3 “分数王国”与“小数王国” 教案
文档属性
| 名称 | 北师大版 五年级数学下册1.3 “分数王国”与“小数王国” 教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 397.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-27 00:00:00 | ||
图片预览

文档简介
第3课时 “分数王国”与“小数王国”
课时目标导航
教学导航
一、教学内容
分数与小数的互化及分数与小数大小比较方法。(教材第7页)
二、教学目标
1.结合比较小数或分数大小的具体例子,探索小数与分数比较大小的方法,掌握分数与小数互化的方法。
2.结合表示分数或小数的直观模型,进一步体会小数与分数互化的方法。
3.进一步体会数学的趣味性,培养学生热爱数学的思想和学习数学的兴趣。
三、重点难点
重点:分数和小数互化的方法和大小比较方法。
难点:分数和小数互化的方法。
四、教学准备
百格图、小数尺。
教学过程
一、情境引入
师:前面我们学习了分数和小数,你们知道它们有什么联系吗?
(课件出示教材第7页情境图)
师:今天,“分数王国”和“小数王国”的很多小朋友来到了我们的课堂,它们要一对一的比大小,你们能应用所学知识,帮助它们吗?(板书课题:“分数王国”与“小数王国”)
二、学习新课
1.比较0.06与的大小。
师:比一比,“小数王国”里的0.06与“分数王国”里的哪个数大?
学生交流、讨论,教师巡视。
指名汇报,把结果归纳汇总如下:
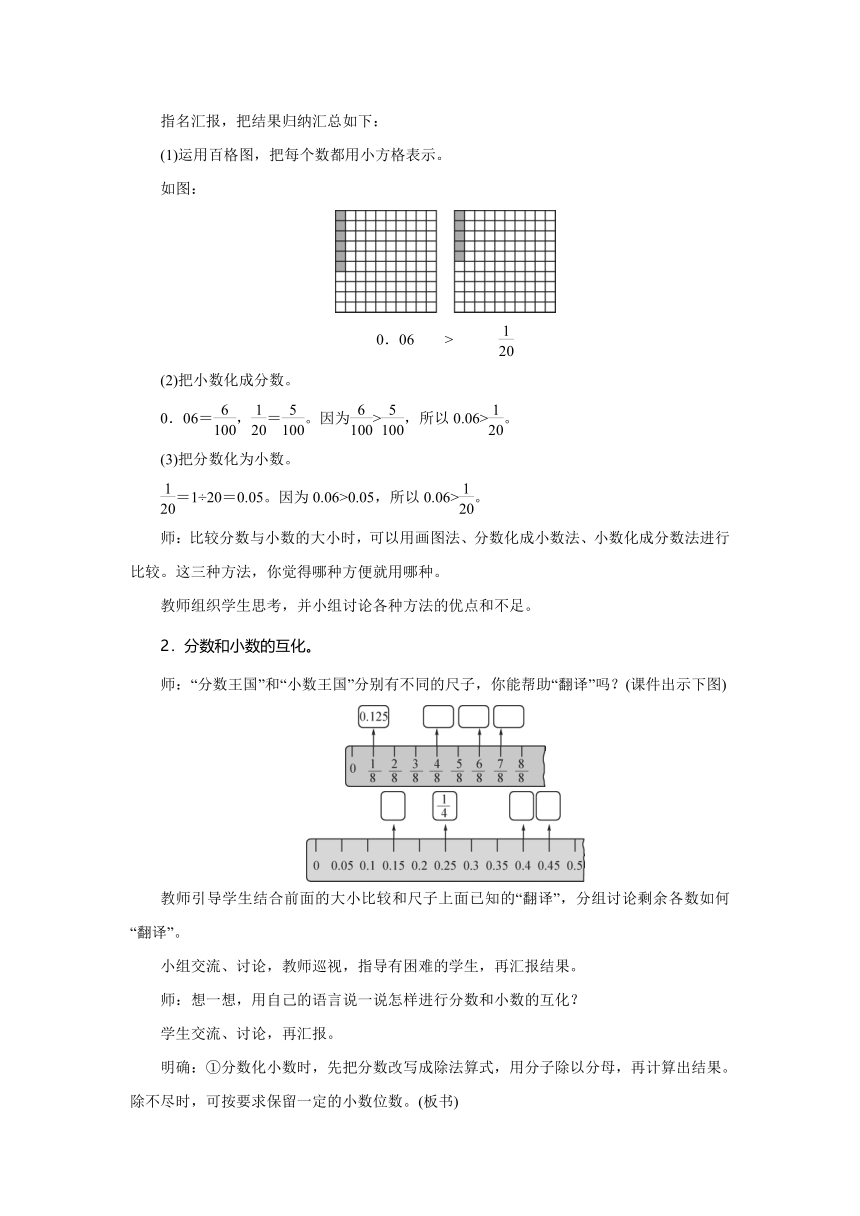
(1)运用百格图,把每个数都用小方格表示。
如图:
0.06 >
(2)把小数化成分数。
0.06=,=。因为>,所以0.06>。
(3)把分数化为小数。
=1÷20=0.05。因为0.06>0.05,所以0.06>。
师:比较分数与小数的大小时,可以用画图法、分数化成小数法、小数化成分数法进行比较。这三种方法,你觉得哪种方便就用哪种。
教师组织学生思考,并小组讨论各种方法的优点和不足。
2.分数和小数的互化。
师:“分数王国”和“小数王国”分别有不同的尺子,你能帮助“翻译”吗?(课件出示下图)
教师引导学生结合前面的大小比较和尺子上面已知的“翻译”,分组讨论剩余各数如何“翻译”。
小组交流、讨论,教师巡视,指导有困难的学生,再汇报结果。
师:想一想,用自己的语言说一说怎样进行分数和小数的互化?
学生交流、讨论,再汇报。
明确:①分数化小数时,先把分数改写成除法算式,用分子除以分母,再计算出结果。除不尽时,可按要求保留一定的小数位数。(板书)
②小数化分数时,根据小数的意义,原来是几位小数,就在1的后面写几个0作分母,把原来的小数去掉小数点作分子,能约分的要约成最简分数。(板书)
3.解决问题。
把下面的小数化成分数,或把分数化成小数,与同伴交流你的做法。
= =
0.24= 1.8=
学生独立完成,再交流,教师指名汇报结果。
①分数可以看成是分子除以分母,就可以将化成0.16,将化成1.75。
②小数可以看成是十分之几、百分之几、千分之几,就可以将0.24化成,化简得,将1.8化成,化简得。
三、巩固反馈
完成教材第8页“练一练”第1~5题。(指名学生回答,集体订正)
第1题:> > <
第2题:
0.65 0.75 0.9 1.05
第3题:
第4题:全错。=0.4 0.05= 0.02=
第5题:略
四、课堂小结
1.这节课我们学习了什么知识?有什么不懂或不理解的地方吗?
2.在分数和小数的互化中要注意些什么?
板书设计
“分数王国”与“小数王国”
0.06>
1.分数化小数:根据分数与除法的关系,把分数写成除法算式来计算。除不尽时,可按要求保留一定的小数位数。
2.小数化分数:根据小数的意义,原来是几位小数,就在1的后面写几个0作分母,把原来的小数去掉小数点作分子,能约分的要约成最简分数。
教学反思
1.本课时教学是借助分数和小数比大小来引出分数和小数互化的方法。教学时,以学生的探究学习为主,教师起引导作用,引导学生采用不同的方法来探究分数和小数的互化。在比较分数与小数的大小时,让学生从多个不同的角度去思考,充分体现了学生是学习的主人。
2.课堂上,应该以“学生发展为本”,认真当好“导演”,充分发挥学生的主动性和积极性,让更多的学生有机会畅所欲言。同时对于课堂上出现的各种问题,教师要见机行事,鼓励学生进步,对学生的不好的习惯要及时指正,支持学生的兴趣发展。
3.我的补充:
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
备课资料参考
典型例题准备
【例题】计算:11----…-。
分析:这是一道连减算式,如果用通分的方法可以计算出结果,过程很繁琐。其实,我们只要根据分数和小数互化的方法,把每一个减数都改写成小数,再运用减法的性质,用被减数减去所有减数的和,就可以很快求出这道题的结果。
解答:11----…-
=11-0.1-0.01-0.001-…-0.0000000001
=11-(0.1+0.01+0.001+…+0.0000000001)
=11-0.1111111111
=10.8888888889
解法归纳:解此类题时,注意观察式子的特点,结合分数和小数互化的方法进行计算。
相关知识阅读
转化思想
转化思想是由一种形式变换成另一种形式的思想,而其本身的大小是不变的,它是一种解决数学问题的重要策略。如分数和小数之间的相互转化就体现了转化思想。
课时目标导航
教学导航
一、教学内容
分数与小数的互化及分数与小数大小比较方法。(教材第7页)
二、教学目标
1.结合比较小数或分数大小的具体例子,探索小数与分数比较大小的方法,掌握分数与小数互化的方法。
2.结合表示分数或小数的直观模型,进一步体会小数与分数互化的方法。
3.进一步体会数学的趣味性,培养学生热爱数学的思想和学习数学的兴趣。
三、重点难点
重点:分数和小数互化的方法和大小比较方法。
难点:分数和小数互化的方法。
四、教学准备
百格图、小数尺。
教学过程
一、情境引入
师:前面我们学习了分数和小数,你们知道它们有什么联系吗?
(课件出示教材第7页情境图)
师:今天,“分数王国”和“小数王国”的很多小朋友来到了我们的课堂,它们要一对一的比大小,你们能应用所学知识,帮助它们吗?(板书课题:“分数王国”与“小数王国”)
二、学习新课
1.比较0.06与的大小。
师:比一比,“小数王国”里的0.06与“分数王国”里的哪个数大?
学生交流、讨论,教师巡视。
指名汇报,把结果归纳汇总如下:
(1)运用百格图,把每个数都用小方格表示。
如图:
0.06 >
(2)把小数化成分数。
0.06=,=。因为>,所以0.06>。
(3)把分数化为小数。
=1÷20=0.05。因为0.06>0.05,所以0.06>。
师:比较分数与小数的大小时,可以用画图法、分数化成小数法、小数化成分数法进行比较。这三种方法,你觉得哪种方便就用哪种。
教师组织学生思考,并小组讨论各种方法的优点和不足。
2.分数和小数的互化。
师:“分数王国”和“小数王国”分别有不同的尺子,你能帮助“翻译”吗?(课件出示下图)
教师引导学生结合前面的大小比较和尺子上面已知的“翻译”,分组讨论剩余各数如何“翻译”。
小组交流、讨论,教师巡视,指导有困难的学生,再汇报结果。
师:想一想,用自己的语言说一说怎样进行分数和小数的互化?
学生交流、讨论,再汇报。
明确:①分数化小数时,先把分数改写成除法算式,用分子除以分母,再计算出结果。除不尽时,可按要求保留一定的小数位数。(板书)
②小数化分数时,根据小数的意义,原来是几位小数,就在1的后面写几个0作分母,把原来的小数去掉小数点作分子,能约分的要约成最简分数。(板书)
3.解决问题。
把下面的小数化成分数,或把分数化成小数,与同伴交流你的做法。
= =
0.24= 1.8=
学生独立完成,再交流,教师指名汇报结果。
①分数可以看成是分子除以分母,就可以将化成0.16,将化成1.75。
②小数可以看成是十分之几、百分之几、千分之几,就可以将0.24化成,化简得,将1.8化成,化简得。
三、巩固反馈
完成教材第8页“练一练”第1~5题。(指名学生回答,集体订正)
第1题:> > <
第2题:
0.65 0.75 0.9 1.05
第3题:
第4题:全错。=0.4 0.05= 0.02=
第5题:略
四、课堂小结
1.这节课我们学习了什么知识?有什么不懂或不理解的地方吗?
2.在分数和小数的互化中要注意些什么?
板书设计
“分数王国”与“小数王国”
0.06>
1.分数化小数:根据分数与除法的关系,把分数写成除法算式来计算。除不尽时,可按要求保留一定的小数位数。
2.小数化分数:根据小数的意义,原来是几位小数,就在1的后面写几个0作分母,把原来的小数去掉小数点作分子,能约分的要约成最简分数。
教学反思
1.本课时教学是借助分数和小数比大小来引出分数和小数互化的方法。教学时,以学生的探究学习为主,教师起引导作用,引导学生采用不同的方法来探究分数和小数的互化。在比较分数与小数的大小时,让学生从多个不同的角度去思考,充分体现了学生是学习的主人。
2.课堂上,应该以“学生发展为本”,认真当好“导演”,充分发挥学生的主动性和积极性,让更多的学生有机会畅所欲言。同时对于课堂上出现的各种问题,教师要见机行事,鼓励学生进步,对学生的不好的习惯要及时指正,支持学生的兴趣发展。
3.我的补充:
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
备课资料参考
典型例题准备
【例题】计算:11----…-。
分析:这是一道连减算式,如果用通分的方法可以计算出结果,过程很繁琐。其实,我们只要根据分数和小数互化的方法,把每一个减数都改写成小数,再运用减法的性质,用被减数减去所有减数的和,就可以很快求出这道题的结果。
解答:11----…-
=11-0.1-0.01-0.001-…-0.0000000001
=11-(0.1+0.01+0.001+…+0.0000000001)
=11-0.1111111111
=10.8888888889
解法归纳:解此类题时,注意观察式子的特点,结合分数和小数互化的方法进行计算。
相关知识阅读
转化思想
转化思想是由一种形式变换成另一种形式的思想,而其本身的大小是不变的,它是一种解决数学问题的重要策略。如分数和小数之间的相互转化就体现了转化思想。
