华东师大版数学八年级上册第13章全等三角形 复习课件(共21张PPT)
文档属性
| 名称 | 华东师大版数学八年级上册第13章全等三角形 复习课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 273.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-26 11:04:44 | ||
图片预览



文档简介
(共21张PPT)
复习题
知识回顾
一、全等三角形概念:
能够 的三角形是全等三角形.
二、全等三角形性质:
全等三角形对应边 .
全等三角形对应角 .
完全重合
相等
相等
知识回顾
三、三角形全等的条件(判定):
1、两边及其 对应相等的两个三角形全等。
简称“ ”
2、两角和它们的 对应相等的两个三角形全
等。简称“ ”
3、两角和其中一角的 对应相等的两个三角形
全等。简称“ ”
4、三边 的两个三角形全等。简称“ ”
5、两个直角三角形的斜边和一条 对应相等
的两个直角三角形全等。简称“ ”
对应相等
SSS
夹角
SAS
夹边
ASA
对边
AAS
直角边
HL
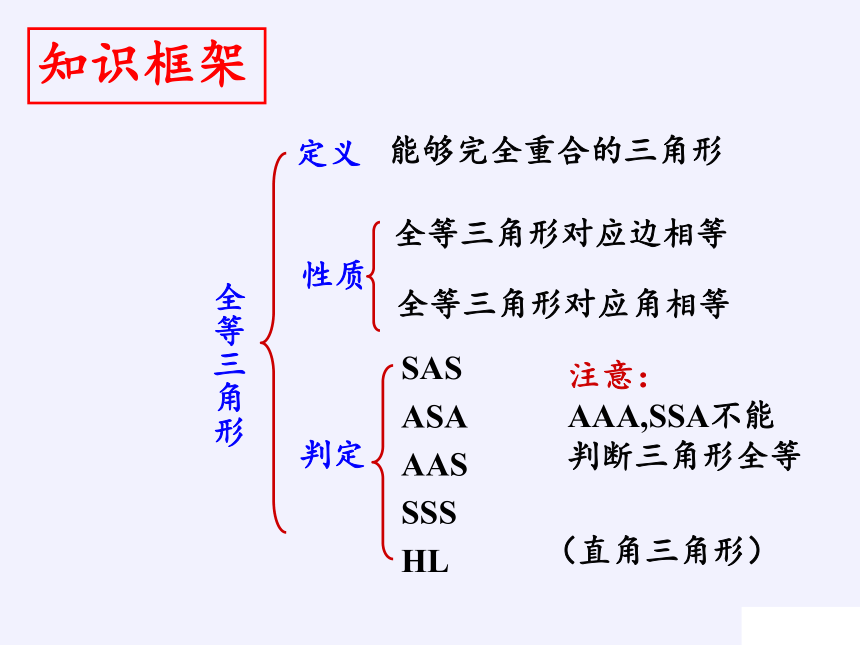
全等三角形
定义
能够完全重合的三角形
性质
全等三角形对应边相等
全等三角形对应角相等
判定
SAS
ASA
AAS
SSS
HL
注意:AAA,SSA不能判断三角形全等
知识框架
(直角三角形)
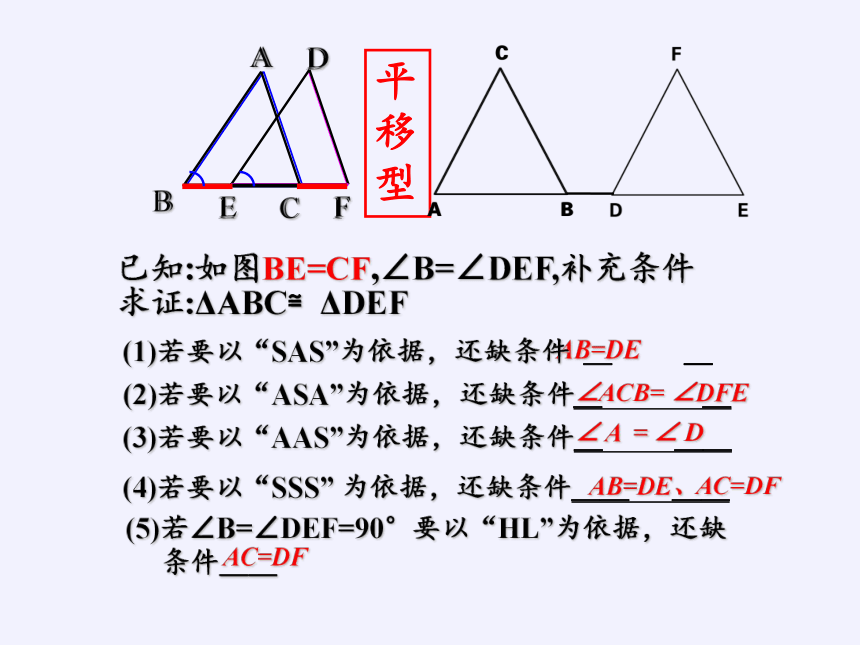
已知:如图BE=CF,∠B=∠DEF,补充条件
求证:ΔABC≌ΔDEF
∠ACB= ∠DFE
AB=DE
AB=DE、AC=DF
A
B
C
D
E
F
D
E
F
A
B
C
∠ A = ∠ D
(1)若要以“SAS”为依据,还缺条件 _ _
(2)若要以“ASA”为依据,还缺条件_ _
(4)若要以“SSS” 为依据,还缺条件__ __
(3)若要以“AAS”为依据,还缺条件_ __
平
移
型
(5)若∠B=∠DEF=90°要以“HL”为依据,还缺
条件__
AC=DF
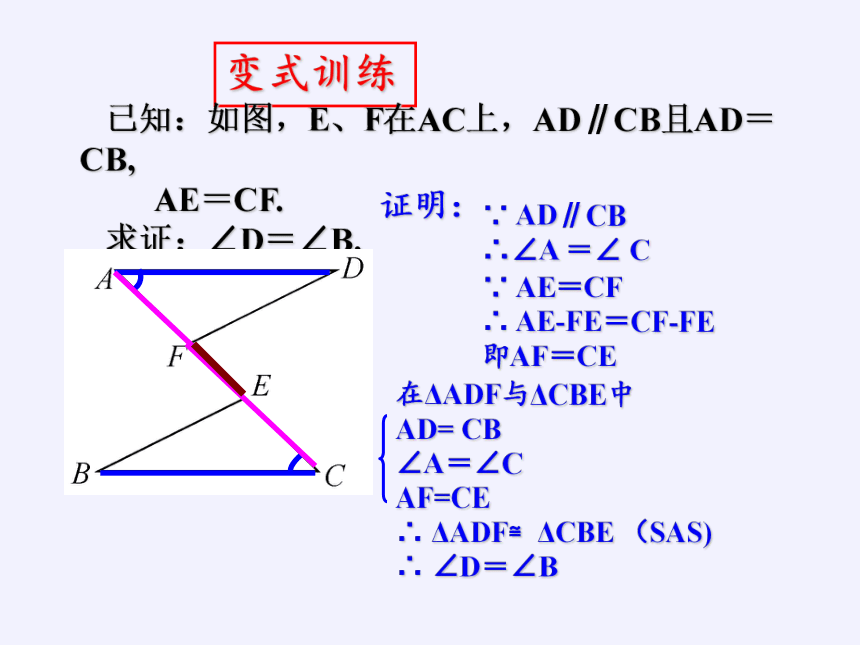
变式训练
已知:如图,E、F在AC上,AD∥CB且AD=CB,
AE=CF.
求证:∠D=∠B.
在ΔADF与ΔCBE中
AD= CB
∠A=∠C
AF=CE
∴ ΔADF≌ΔCBE (SAS)
∴ ∠D=∠B
证明:
∵ AD∥CB
∴∠A =∠ C
∵ AE=CF
∴ AE-FE=CF-FE
即AF=CE
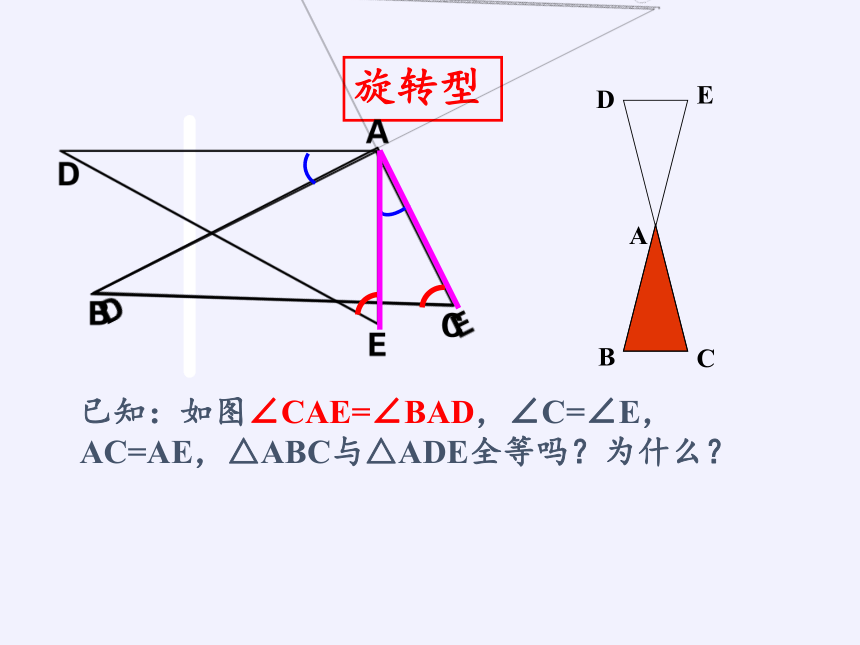
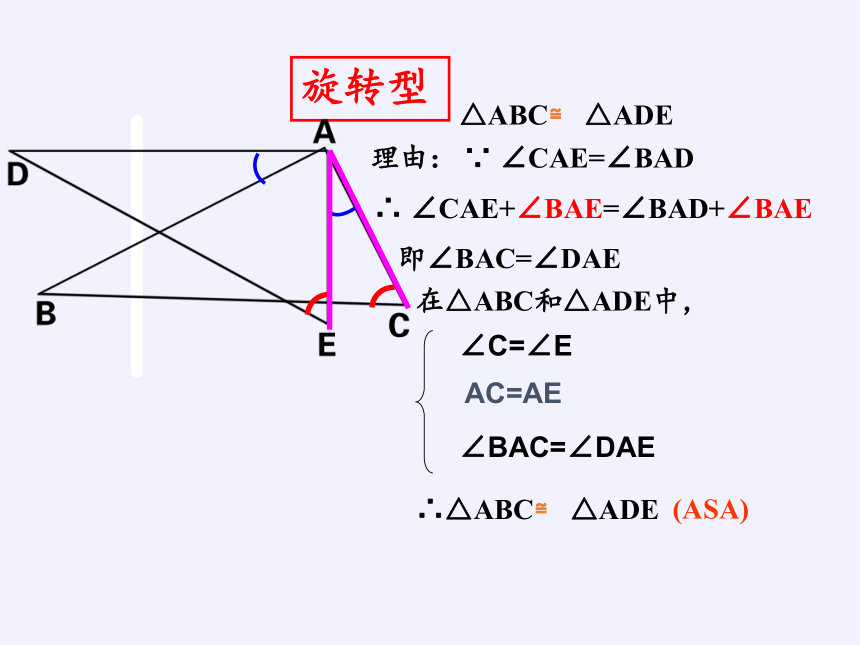
旋转型
已知:如图∠CAE=∠BAD,∠C=∠E,AC=AE,△ABC与△ADE全等吗?为什么?
A
B
C
E
D
旋转型
∵ ∠CAE=∠BAD
∴ ∠CAE+∠BAE=∠BAD+∠BAE
即∠BAC=∠DAE
在△ABC和△ADE中,
∴△ABC≌ △ADE
AC=AE
∠BAC=∠DAE
∠C=∠E
(ASA)
△ABC≌ △ADE
理由:
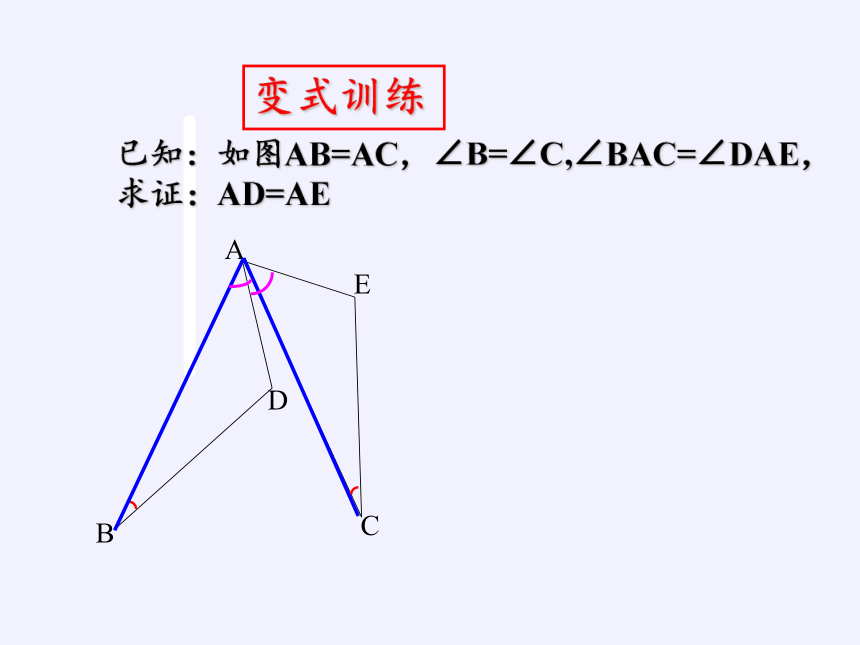
已知:如图AB=AC,∠B=∠C,∠BAC=∠DAE,
求证:AD=AE
D
A
B
E
C
变式训练
轴对称型
D
A
C
B
A
D
B
C
O
隐含条件—对顶角 ∠AOD=∠BOC
轴对称型
如图,已知AD=BC,∠D=∠C.
求证: ∠A= ∠B.
证明:在△AOD和△BOC中
∠AOD=∠BOC
∠D=∠C
AD=BC
∴ △AOD ≌ △BOC(AAS)
∴ ∠A= ∠B
变式训练1
A
D
B
C
O
如图,已知AD=BC, . 求证: ∠A= ∠B.
隐含条件—公共边 DC=DC
分析:已知两边
→找第三边 ( SSS )
证明:连结DC
在△ADC和△BCD中
AD=BC
AC=BD
DC=CD
∴ △ADC ≌ △BCD(SSS)
∴ ∠A= ∠B
AC=BD
∠D=∠C
C
B
D
A
如图,已知AB=AD,要使△ABC≌△ADC,需要添加的一个条件是__________.
找夹角
找第三边
已知两组边
∠BAC=∠DAC(SAS)
BC=DC (SSS)
隐含条件—公共边 AC=AC
轴对称型
找直角
∠B=∠D=90°(HL)
如图∠B=∠D ,∠1=∠2,AB = AD
求证:ΔABE≌ΔADC
在ΔABE与ΔADC中
∠B=∠D
AB = AD
∠ BAE=∠ DAC
∴ ΔABE≌ΔADC (ASA)
A
C
D
B
E
1
2
举一反三
D
C
B
A
证明:
∵∠1= ∠ 2
∴∠ 1+ ∠CAE=∠ 2+∠ CAE
即∠BAE=∠DAC
隐含条件—公共角
D
B
A
C
D
B
A
E
C
如图,已知AC=AE,要使△ACD≌△AEB,需要添加的一个条件是__________。
已知一组边一组角
找夹这个角的另一边
找夹这条边的另一角
找边的对角
AB=AD
∠C=∠E
∠ADC=∠ABE
(SAS)
(ASA)
(AAS)
A
C
D
B
E
如图,已知 ,要使△ACD≌△AEB,需要添加的一个条件是__________。
找任一角
已知一组边及其对角
(AAS)
∠C=∠E
或者
∠ADC=∠ABE
A
C
D
B
E
添加AC=AE或者AB=AD可以吗?
要防止出现“SSA”的错误!
DC=BE
AC=AE
E
D
B
C
O
A
已知:如图,BE和DC交于点O,
∠B=∠D,BE=DC
求证:BC=DE
变式训练2
知识小结
通过这节课的复习,我们进一步理解和掌握了全等三角形的判定及其基本图形,这个内容在整个初中几何教材中有着举足轻重的地位,它是一个基本的几何工具,很多的几何问题需要用它来解决。例如在证明两条线段相等或两个角相等时,利用全等三角形就是我们通常考虑的首选方法。这个内容在中考考标中的要求层次也是最高的,固涉及试题所占的比分也是较高的,因此请同学们务必要熟练掌握!
布置作业
课本 P79 1、2、4、5
数学就像一场战役
懂得运筹帷幄
才能决胜千里
结束语
谢 谢
复习题
知识回顾
一、全等三角形概念:
能够 的三角形是全等三角形.
二、全等三角形性质:
全等三角形对应边 .
全等三角形对应角 .
完全重合
相等
相等
知识回顾
三、三角形全等的条件(判定):
1、两边及其 对应相等的两个三角形全等。
简称“ ”
2、两角和它们的 对应相等的两个三角形全
等。简称“ ”
3、两角和其中一角的 对应相等的两个三角形
全等。简称“ ”
4、三边 的两个三角形全等。简称“ ”
5、两个直角三角形的斜边和一条 对应相等
的两个直角三角形全等。简称“ ”
对应相等
SSS
夹角
SAS
夹边
ASA
对边
AAS
直角边
HL
全等三角形
定义
能够完全重合的三角形
性质
全等三角形对应边相等
全等三角形对应角相等
判定
SAS
ASA
AAS
SSS
HL
注意:AAA,SSA不能判断三角形全等
知识框架
(直角三角形)
已知:如图BE=CF,∠B=∠DEF,补充条件
求证:ΔABC≌ΔDEF
∠ACB= ∠DFE
AB=DE
AB=DE、AC=DF
A
B
C
D
E
F
D
E
F
A
B
C
∠ A = ∠ D
(1)若要以“SAS”为依据,还缺条件 _ _
(2)若要以“ASA”为依据,还缺条件_ _
(4)若要以“SSS” 为依据,还缺条件__ __
(3)若要以“AAS”为依据,还缺条件_ __
平
移
型
(5)若∠B=∠DEF=90°要以“HL”为依据,还缺
条件__
AC=DF
变式训练
已知:如图,E、F在AC上,AD∥CB且AD=CB,
AE=CF.
求证:∠D=∠B.
在ΔADF与ΔCBE中
AD= CB
∠A=∠C
AF=CE
∴ ΔADF≌ΔCBE (SAS)
∴ ∠D=∠B
证明:
∵ AD∥CB
∴∠A =∠ C
∵ AE=CF
∴ AE-FE=CF-FE
即AF=CE
旋转型
已知:如图∠CAE=∠BAD,∠C=∠E,AC=AE,△ABC与△ADE全等吗?为什么?
A
B
C
E
D
旋转型
∵ ∠CAE=∠BAD
∴ ∠CAE+∠BAE=∠BAD+∠BAE
即∠BAC=∠DAE
在△ABC和△ADE中,
∴△ABC≌ △ADE
AC=AE
∠BAC=∠DAE
∠C=∠E
(ASA)
△ABC≌ △ADE
理由:
已知:如图AB=AC,∠B=∠C,∠BAC=∠DAE,
求证:AD=AE
D
A
B
E
C
变式训练
轴对称型
D
A
C
B
A
D
B
C
O
隐含条件—对顶角 ∠AOD=∠BOC
轴对称型
如图,已知AD=BC,∠D=∠C.
求证: ∠A= ∠B.
证明:在△AOD和△BOC中
∠AOD=∠BOC
∠D=∠C
AD=BC
∴ △AOD ≌ △BOC(AAS)
∴ ∠A= ∠B
变式训练1
A
D
B
C
O
如图,已知AD=BC, . 求证: ∠A= ∠B.
隐含条件—公共边 DC=DC
分析:已知两边
→找第三边 ( SSS )
证明:连结DC
在△ADC和△BCD中
AD=BC
AC=BD
DC=CD
∴ △ADC ≌ △BCD(SSS)
∴ ∠A= ∠B
AC=BD
∠D=∠C
C
B
D
A
如图,已知AB=AD,要使△ABC≌△ADC,需要添加的一个条件是__________.
找夹角
找第三边
已知两组边
∠BAC=∠DAC(SAS)
BC=DC (SSS)
隐含条件—公共边 AC=AC
轴对称型
找直角
∠B=∠D=90°(HL)
如图∠B=∠D ,∠1=∠2,AB = AD
求证:ΔABE≌ΔADC
在ΔABE与ΔADC中
∠B=∠D
AB = AD
∠ BAE=∠ DAC
∴ ΔABE≌ΔADC (ASA)
A
C
D
B
E
1
2
举一反三
D
C
B
A
证明:
∵∠1= ∠ 2
∴∠ 1+ ∠CAE=∠ 2+∠ CAE
即∠BAE=∠DAC
隐含条件—公共角
D
B
A
C
D
B
A
E
C
如图,已知AC=AE,要使△ACD≌△AEB,需要添加的一个条件是__________。
已知一组边一组角
找夹这个角的另一边
找夹这条边的另一角
找边的对角
AB=AD
∠C=∠E
∠ADC=∠ABE
(SAS)
(ASA)
(AAS)
A
C
D
B
E
如图,已知 ,要使△ACD≌△AEB,需要添加的一个条件是__________。
找任一角
已知一组边及其对角
(AAS)
∠C=∠E
或者
∠ADC=∠ABE
A
C
D
B
E
添加AC=AE或者AB=AD可以吗?
要防止出现“SSA”的错误!
DC=BE
AC=AE
E
D
B
C
O
A
已知:如图,BE和DC交于点O,
∠B=∠D,BE=DC
求证:BC=DE
变式训练2
知识小结
通过这节课的复习,我们进一步理解和掌握了全等三角形的判定及其基本图形,这个内容在整个初中几何教材中有着举足轻重的地位,它是一个基本的几何工具,很多的几何问题需要用它来解决。例如在证明两条线段相等或两个角相等时,利用全等三角形就是我们通常考虑的首选方法。这个内容在中考考标中的要求层次也是最高的,固涉及试题所占的比分也是较高的,因此请同学们务必要熟练掌握!
布置作业
课本 P79 1、2、4、5
数学就像一场战役
懂得运筹帷幄
才能决胜千里
结束语
谢 谢
