人教版七年级上册数学4.3.1 角课件(共49张PPT)
文档属性
| 名称 | 人教版七年级上册数学4.3.1 角课件(共49张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-26 11:25:01 | ||
图片预览









文档简介
(共49张PPT)
角(二)
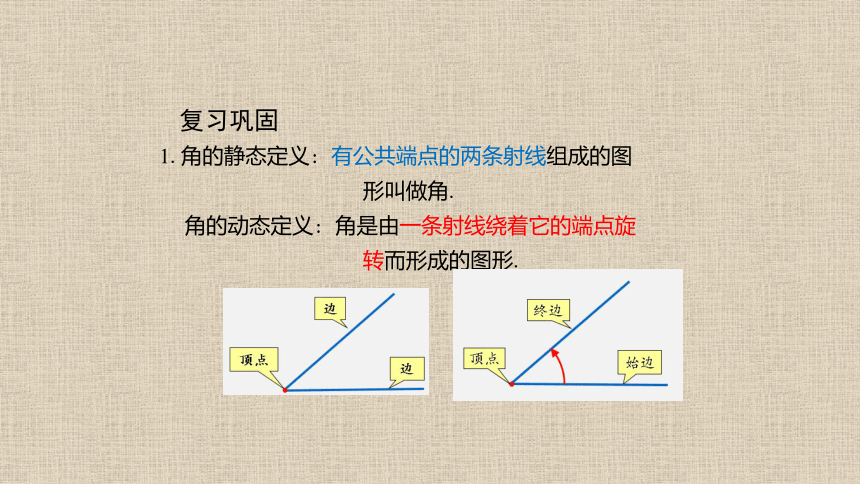
1.角的静态定义: 有公共端点的两条射线组成的图
形叫做角.
角的动态定义: 角是由一条射线绕着它的端点旋
转而形成的图形.
复习巩固
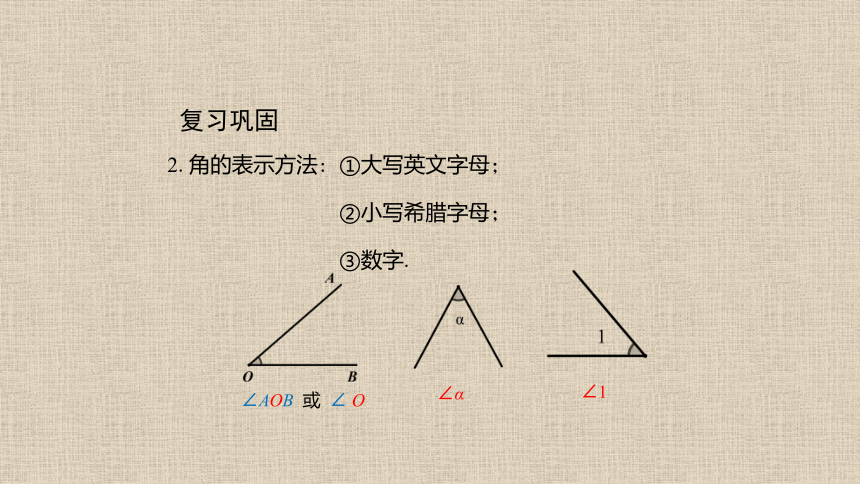
2.角的表示方法: ①大写英文字母;
②小写希腊字母;
③数字.
∠AOB 或 ∠ O
∠α
∠1
复习巩固
3. 角的换算:
1周角=360 , 1平角=180 ,
1 =60 , 1 =60 .
复习巩固
(1)48 39 20 +67 31 45 ;
解: 48 39 20 +67 31 45
=(48+67) +(39+31) +(20+45)
=115 +70 +65
=115 +1 +10 + 1 +5
=116 11 5 ;
同单位直接相加
每满60进1
例1 计算:
例题讲解
(2)75 18 -37 30 ;
解: 75 18 -37 30
=74 78 -37 30
=(74- 37) +(78-30)
=37 48 ;
同单位直接相减
借1 作60
例1 计算:
例题讲解
(3)21 17 30 ×5;
解: 21 17 30 ×5
=(21 +17 + 30 )×5
=21 ×5+17 ×5+30 ×5
=105 +85 +150
=105 +1 +25 +2 +30
=106 27 30 ;
乘法分配律
化为和
每满60进1
例1 计算:
例题讲解
(4)360 ÷7(精确到分)
解: 360 ÷7
=51 +3 ÷7
=51 +180 ÷7
≈51 +25.7
≈51 26 .
精确到分,要先取到小数点后1位,然后再四舍五入.
例1 计算:
例题讲解
法1:
(4)360 ÷7(精确到分)
360 ÷7
≈51.43
=51 +(0.43×60)
=51 +25.8
≈51 26 .
四舍五入,精确到分.
法2:
例1 计算:
例题讲解
1.和差运算,先把度、分、秒分别求和或作差,
然后根据满60进1,或借1作60,计算得到最后
的结果.
小结:
2.倍分运算,先把度、分、秒同时乘以倍数或除
以份数,再根据题目的要求,计算得到最后的
结果.
思考:根据学习线段的经验,接下来将要学习角的什么内容?
角的大小比较和角的运算.
学习新知
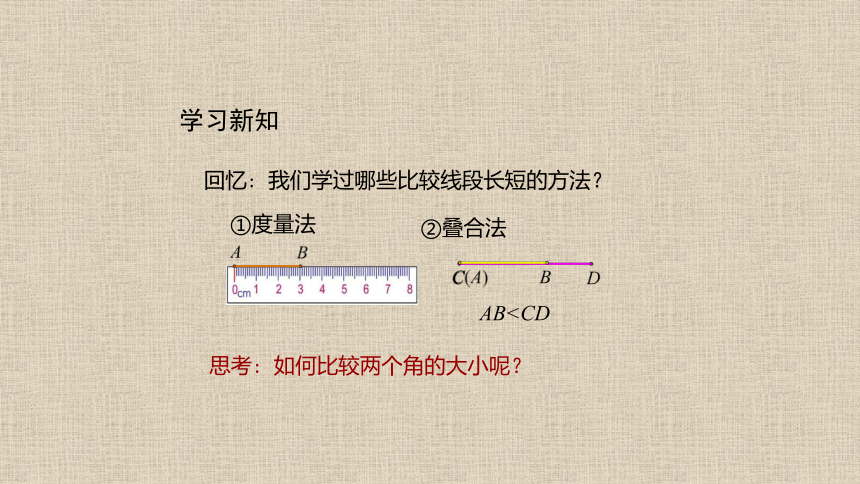
回忆: 我们学过哪些比较线段长短的方法?
①度量法
思考: 如何比较两个角的大小呢?
②叠合法
AB学习新知
如何比较∠AOB与∠A O B 的大小呢?
方法1(度量法):用量角器量出∠AOB与∠A O B 的度数,就可以比较它们的大小了.
图中∠AOB=51 ,∠A O B =56 ,
所以∠AOB<∠A O B .
1.角的大小比较
51
56
学习新知
还有什么方法比较∠AOB与∠A O B 的大小呢?
方法2(叠合法):将两个角的一边重合在一起,两个角的另一边落在第一边的同一侧,观察这两边的位置,就可以确定两个角的大小了.
1.角的大小比较
学习新知
固定∠AOB的位置,让∠A O B 的边O A 与OA重合,
O B 与OB在OA的同一侧,
①若O B 在∠AOB内部,则∠A O B <∠AOB;
1.角的大小比较
学习新知
固定∠AOB的位置,让∠A O B 的边O A 与OA重合,
O B 与OB在OA的同一侧,
②若O B 与OB重合,则∠A O B =∠AOB;
学习新知
1.角的大小比较
固定∠AOB的位置,让∠A O B 的边O A 与OA重合,
O B 与OB在OA的同一侧,
③若O B 在∠AOB外部,则∠A O B >∠AOB;
学习新知
1.角的大小比较
两个角的三种大小关系:小于,等于或大于.
学习新知
∠ABC=50
∠DEF=50
∠ABC=∠DEF
判断下图中∠ABC与∠DEF的大小关系.
度量法
学习新知
角的大小与角的两边张开的大小有关;
与角的边画出的长短无关.
叠合法
判断下图中∠ABC与∠DEF的大小关系.
∠ABC=∠DEF
学习新知
E(B)
例2 如图,用“<、= 或>”填空.
(1)∠AOD____∠AOC;
>
例题讲解
例2 如图,用“<、= 或>”填空.
(1)∠AOD____∠AOC;
(2)∠AOB____∠BOC ;
>
例题讲解
>
例2 如图,用“<、= 或>”填空.
(1)∠AOD____∠AOC;
(2)∠AOB____∠BOC ;
(3)∠COD____∠BOC ;
>
例题讲解
>
<
例2 如图,用“<、= 或>”填空.
(1)∠AOD____∠AOC;
(2)∠AOB____∠BOC ;
(3)∠COD____∠BOC ;
(4)∠AOC+∠BOD____∠AOB.
>
例题讲解
>
<
<
观察: 图中共有几个角?
图中有∠AOB,∠BOC和∠AOC ,
共3个角.
思考:能用等式表示它们之间满足的数量关系吗?
学习新知
∠AOC是∠AOB与∠BOC的和,
记作∠AOC=∠AOB+∠BOC;
∠AOB是∠AOC与∠BOC的差,
记作∠AOB=∠AOC-∠BOC;
类似地,∠BOC=∠AOC-∠AOB.
2.角的和差
学习新知
例3 如图,填空:
(1)∠AOC+∠COD=______;
∠AOD
例题讲解
例3 如图,填空:
(1)∠AOC+∠COD=______;
(2)∠BOD+∠COD+∠AOC=_______;
∠AOD
例题讲解
∠AOB
例3 如图,填空:
(3)∠COD =∠AOD-_______
=______-∠BOD
=∠AOB-_______-_______;
例题讲解
∠AOC
例3 如图,填空:
(3)∠COD =∠AOD-_______
=______-∠BOD
=∠AOB-_______-_______;
例题讲解
∠AOC
∠BOC
例3 如图,填空:
(3)∠COD =∠AOD-_______
=______-∠BOD
=∠AOB-_______-_______;
例题讲解
∠AOC
∠BOC
∠AOC
∠BOD
例3 如图,填空:
(4)∠AOD=_______+_______
=_______-_______.
例题讲解
∠AOC
∠COD
例3 如图,填空:
(4)∠AOD=_______+_______
=_______-_______.
例题讲解
∠AOC
∠COD
∠AOB
∠BOD
例4(1)一副三角尺中包含哪些度数的角?
一副三角尺中含有30 ,45 ,60 ,90 的角.
30
90
60
45
90
45
例题讲解
例4(2)用一副三角尺可以画出哪些大于0度小于180度的角?
这些角有什么共同点?
用一个三角尺能画出30 ,45 ,60 ,90 的角.
例题讲解
45 +30 =75
45 +60 =105
用一副三角尺可以拼出以下图形
例题讲解
90 + 30 =120
90 + 45 =135
用一副三角尺可以拼出以下图形
例题讲解
90 +60 =150
45 -30 =15
用一副三角尺可以拼出以下图形
15
例题讲解
例4(2)用一副三角尺可以画出哪些大于0度小于180度的角?这些角有什么共同点?
一副三角尺可以画出15 ,30 ,45 ,60 ,75 ,90 ,105 ,120 ,135 ,150 ,165 .
这些角的度数都是15的倍数.
15
例题讲解
例5 已知射线OA,若从点O再引两条射线OB,OC,
使∠AOB=80 ,∠BOC=30 ,求∠AOC的度数.
分析:根据题意,射线OC可能在∠AOB外部或内部,
例题讲解
解:根据题意,射线OC可能在∠AOB外部或内部,
(1) 如图1,当OC在∠AOB外部时,
因为∠AOC=∠AOB+∠BOC ,
∠AOB=80 ,∠BOC=30 ,
所以∠AOC= 80 +30 =110 ;
例题讲解
例5 已知射线OA,若从点O再引两条射线OB,OC,
使∠AOB=80 ,∠BOC=30 ,求∠AOC的度数.
(2) 如图2,当OC在∠AOB内部时,
因为 ∠AOC=∠AOB-∠BOC ,
∠AOB=80 ,∠BOC=30 ,
所以∠AOC= 80 -30 =50 .
答: ∠AOC的度数为110 或50 .
例题讲解
例5 已知射线OA,若从点O再引两条射线OB,OC,
使∠AOB=80 ,∠BOC=30 ,求∠AOC的度数.
1.度量法:
用量角器量出∠AOB与∠A O B 的度数,就可以
比较它们的大小了.
比如∠AOB=51 ,∠A O B =56 ,
所以∠AOB<∠A O B .
51
56
课堂小结
一、角的大小的比较
2.叠合法:
将两个角的一边重合在一起,两个角的另一边落在第一边的同一侧,观察这两边的位置,就可以确定两个角的大小了.
一、角的大小的比较
课堂小结
如图,∠AOC是∠AOB与∠BOC的和,
记作∠AOC=∠AOB+∠BOC;
∠AOB是∠AOC与∠BOC的差,
记作∠AOB=∠AOC-∠BOC.
两个角的和或差,仍然是一个角.
二、角的和或差
课堂小结
数学思想方法:
在本节课内容的学习过程中,通过类比线段长短的比较,学习了角的大小比较,这体现了我们在数学学习中经常用到的类比的数学思想;在没有给定图形时,我们运用分类讨论的思想画出了题目所包含的全部图形.
课堂小结
已知,如图,从O点引四条射线OA,OB,OC,
OD,若∠AOB, ∠BOC, ∠COD, ∠DOA
的度数之比为1﹕2﹕3﹕4.
求∠BOC的度数.
课后拓展
x
2x
3x
4x
已知,如图,从O点引四条射线OA,OB,OC,
OD,若∠AOB, ∠BOC, ∠COD, ∠DOA
的度数之比为1﹕2﹕3﹕4.
求∠BOC的度数.
课后拓展
x
2x
3x
4x
分析:∠AOB+∠BOC+∠COD+∠DOA=360 ,
根据角的比为1﹕2﹕3﹕4 ,
设 ∠AOB=x ,
可得 ∠BOC=2x ,∠COD=3x ,∠DOA=4x ,
所以 x+2x+3x+4x=360.
解:设∠AOB=x ,
根据∠AOB,∠BOC,∠COD,∠DOA度数之比
为1﹕2﹕3﹕4 ,
可得 ∠BOC=2x ,∠COD=3x ,∠DOA=4x ,
因为 ∠AOB+∠BOC+∠COD+∠DOA=360 (周角的定义),
所以 x+2x+3x+4x=360,
解得 x=36.
所以 ∠BOC=2x =72 .
课后拓展
x
2x
3x
4x
角(二)
1.角的静态定义: 有公共端点的两条射线组成的图
形叫做角.
角的动态定义: 角是由一条射线绕着它的端点旋
转而形成的图形.
复习巩固
2.角的表示方法: ①大写英文字母;
②小写希腊字母;
③数字.
∠AOB 或 ∠ O
∠α
∠1
复习巩固
3. 角的换算:
1周角=360 , 1平角=180 ,
1 =60 , 1 =60 .
复习巩固
(1)48 39 20 +67 31 45 ;
解: 48 39 20 +67 31 45
=(48+67) +(39+31) +(20+45)
=115 +70 +65
=115 +1 +10 + 1 +5
=116 11 5 ;
同单位直接相加
每满60进1
例1 计算:
例题讲解
(2)75 18 -37 30 ;
解: 75 18 -37 30
=74 78 -37 30
=(74- 37) +(78-30)
=37 48 ;
同单位直接相减
借1 作60
例1 计算:
例题讲解
(3)21 17 30 ×5;
解: 21 17 30 ×5
=(21 +17 + 30 )×5
=21 ×5+17 ×5+30 ×5
=105 +85 +150
=105 +1 +25 +2 +30
=106 27 30 ;
乘法分配律
化为和
每满60进1
例1 计算:
例题讲解
(4)360 ÷7(精确到分)
解: 360 ÷7
=51 +3 ÷7
=51 +180 ÷7
≈51 +25.7
≈51 26 .
精确到分,要先取到小数点后1位,然后再四舍五入.
例1 计算:
例题讲解
法1:
(4)360 ÷7(精确到分)
360 ÷7
≈51.43
=51 +(0.43×60)
=51 +25.8
≈51 26 .
四舍五入,精确到分.
法2:
例1 计算:
例题讲解
1.和差运算,先把度、分、秒分别求和或作差,
然后根据满60进1,或借1作60,计算得到最后
的结果.
小结:
2.倍分运算,先把度、分、秒同时乘以倍数或除
以份数,再根据题目的要求,计算得到最后的
结果.
思考:根据学习线段的经验,接下来将要学习角的什么内容?
角的大小比较和角的运算.
学习新知
回忆: 我们学过哪些比较线段长短的方法?
①度量法
思考: 如何比较两个角的大小呢?
②叠合法
AB
如何比较∠AOB与∠A O B 的大小呢?
方法1(度量法):用量角器量出∠AOB与∠A O B 的度数,就可以比较它们的大小了.
图中∠AOB=51 ,∠A O B =56 ,
所以∠AOB<∠A O B .
1.角的大小比较
51
56
学习新知
还有什么方法比较∠AOB与∠A O B 的大小呢?
方法2(叠合法):将两个角的一边重合在一起,两个角的另一边落在第一边的同一侧,观察这两边的位置,就可以确定两个角的大小了.
1.角的大小比较
学习新知
固定∠AOB的位置,让∠A O B 的边O A 与OA重合,
O B 与OB在OA的同一侧,
①若O B 在∠AOB内部,则∠A O B <∠AOB;
1.角的大小比较
学习新知
固定∠AOB的位置,让∠A O B 的边O A 与OA重合,
O B 与OB在OA的同一侧,
②若O B 与OB重合,则∠A O B =∠AOB;
学习新知
1.角的大小比较
固定∠AOB的位置,让∠A O B 的边O A 与OA重合,
O B 与OB在OA的同一侧,
③若O B 在∠AOB外部,则∠A O B >∠AOB;
学习新知
1.角的大小比较
两个角的三种大小关系:小于,等于或大于.
学习新知
∠ABC=50
∠DEF=50
∠ABC=∠DEF
判断下图中∠ABC与∠DEF的大小关系.
度量法
学习新知
角的大小与角的两边张开的大小有关;
与角的边画出的长短无关.
叠合法
判断下图中∠ABC与∠DEF的大小关系.
∠ABC=∠DEF
学习新知
E(B)
例2 如图,用“<、= 或>”填空.
(1)∠AOD____∠AOC;
>
例题讲解
例2 如图,用“<、= 或>”填空.
(1)∠AOD____∠AOC;
(2)∠AOB____∠BOC ;
>
例题讲解
>
例2 如图,用“<、= 或>”填空.
(1)∠AOD____∠AOC;
(2)∠AOB____∠BOC ;
(3)∠COD____∠BOC ;
>
例题讲解
>
<
例2 如图,用“<、= 或>”填空.
(1)∠AOD____∠AOC;
(2)∠AOB____∠BOC ;
(3)∠COD____∠BOC ;
(4)∠AOC+∠BOD____∠AOB.
>
例题讲解
>
<
<
观察: 图中共有几个角?
图中有∠AOB,∠BOC和∠AOC ,
共3个角.
思考:能用等式表示它们之间满足的数量关系吗?
学习新知
∠AOC是∠AOB与∠BOC的和,
记作∠AOC=∠AOB+∠BOC;
∠AOB是∠AOC与∠BOC的差,
记作∠AOB=∠AOC-∠BOC;
类似地,∠BOC=∠AOC-∠AOB.
2.角的和差
学习新知
例3 如图,填空:
(1)∠AOC+∠COD=______;
∠AOD
例题讲解
例3 如图,填空:
(1)∠AOC+∠COD=______;
(2)∠BOD+∠COD+∠AOC=_______;
∠AOD
例题讲解
∠AOB
例3 如图,填空:
(3)∠COD =∠AOD-_______
=______-∠BOD
=∠AOB-_______-_______;
例题讲解
∠AOC
例3 如图,填空:
(3)∠COD =∠AOD-_______
=______-∠BOD
=∠AOB-_______-_______;
例题讲解
∠AOC
∠BOC
例3 如图,填空:
(3)∠COD =∠AOD-_______
=______-∠BOD
=∠AOB-_______-_______;
例题讲解
∠AOC
∠BOC
∠AOC
∠BOD
例3 如图,填空:
(4)∠AOD=_______+_______
=_______-_______.
例题讲解
∠AOC
∠COD
例3 如图,填空:
(4)∠AOD=_______+_______
=_______-_______.
例题讲解
∠AOC
∠COD
∠AOB
∠BOD
例4(1)一副三角尺中包含哪些度数的角?
一副三角尺中含有30 ,45 ,60 ,90 的角.
30
90
60
45
90
45
例题讲解
例4(2)用一副三角尺可以画出哪些大于0度小于180度的角?
这些角有什么共同点?
用一个三角尺能画出30 ,45 ,60 ,90 的角.
例题讲解
45 +30 =75
45 +60 =105
用一副三角尺可以拼出以下图形
例题讲解
90 + 30 =120
90 + 45 =135
用一副三角尺可以拼出以下图形
例题讲解
90 +60 =150
45 -30 =15
用一副三角尺可以拼出以下图形
15
例题讲解
例4(2)用一副三角尺可以画出哪些大于0度小于180度的角?这些角有什么共同点?
一副三角尺可以画出15 ,30 ,45 ,60 ,75 ,90 ,105 ,120 ,135 ,150 ,165 .
这些角的度数都是15的倍数.
15
例题讲解
例5 已知射线OA,若从点O再引两条射线OB,OC,
使∠AOB=80 ,∠BOC=30 ,求∠AOC的度数.
分析:根据题意,射线OC可能在∠AOB外部或内部,
例题讲解
解:根据题意,射线OC可能在∠AOB外部或内部,
(1) 如图1,当OC在∠AOB外部时,
因为∠AOC=∠AOB+∠BOC ,
∠AOB=80 ,∠BOC=30 ,
所以∠AOC= 80 +30 =110 ;
例题讲解
例5 已知射线OA,若从点O再引两条射线OB,OC,
使∠AOB=80 ,∠BOC=30 ,求∠AOC的度数.
(2) 如图2,当OC在∠AOB内部时,
因为 ∠AOC=∠AOB-∠BOC ,
∠AOB=80 ,∠BOC=30 ,
所以∠AOC= 80 -30 =50 .
答: ∠AOC的度数为110 或50 .
例题讲解
例5 已知射线OA,若从点O再引两条射线OB,OC,
使∠AOB=80 ,∠BOC=30 ,求∠AOC的度数.
1.度量法:
用量角器量出∠AOB与∠A O B 的度数,就可以
比较它们的大小了.
比如∠AOB=51 ,∠A O B =56 ,
所以∠AOB<∠A O B .
51
56
课堂小结
一、角的大小的比较
2.叠合法:
将两个角的一边重合在一起,两个角的另一边落在第一边的同一侧,观察这两边的位置,就可以确定两个角的大小了.
一、角的大小的比较
课堂小结
如图,∠AOC是∠AOB与∠BOC的和,
记作∠AOC=∠AOB+∠BOC;
∠AOB是∠AOC与∠BOC的差,
记作∠AOB=∠AOC-∠BOC.
两个角的和或差,仍然是一个角.
二、角的和或差
课堂小结
数学思想方法:
在本节课内容的学习过程中,通过类比线段长短的比较,学习了角的大小比较,这体现了我们在数学学习中经常用到的类比的数学思想;在没有给定图形时,我们运用分类讨论的思想画出了题目所包含的全部图形.
课堂小结
已知,如图,从O点引四条射线OA,OB,OC,
OD,若∠AOB, ∠BOC, ∠COD, ∠DOA
的度数之比为1﹕2﹕3﹕4.
求∠BOC的度数.
课后拓展
x
2x
3x
4x
已知,如图,从O点引四条射线OA,OB,OC,
OD,若∠AOB, ∠BOC, ∠COD, ∠DOA
的度数之比为1﹕2﹕3﹕4.
求∠BOC的度数.
课后拓展
x
2x
3x
4x
分析:∠AOB+∠BOC+∠COD+∠DOA=360 ,
根据角的比为1﹕2﹕3﹕4 ,
设 ∠AOB=x ,
可得 ∠BOC=2x ,∠COD=3x ,∠DOA=4x ,
所以 x+2x+3x+4x=360.
解:设∠AOB=x ,
根据∠AOB,∠BOC,∠COD,∠DOA度数之比
为1﹕2﹕3﹕4 ,
可得 ∠BOC=2x ,∠COD=3x ,∠DOA=4x ,
因为 ∠AOB+∠BOC+∠COD+∠DOA=360 (周角的定义),
所以 x+2x+3x+4x=360,
解得 x=36.
所以 ∠BOC=2x =72 .
课后拓展
x
2x
3x
4x
