小学数学北师大版五年级下4.3长方体的体积 课件(共25张PPT)
文档属性
| 名称 | 小学数学北师大版五年级下4.3长方体的体积 课件(共25张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-27 06:30:19 | ||
图片预览



文档简介
(共25张PPT)
第3课时 长方体的体积
四 长方体(二)
一、复习引入
我们以前学习过长方形、正方形的面积公式,谁来说一说怎么计算长方形和正方形的面积呢?
一、复习引入
长方形的面积=长×宽
正方形的面积=边长×边长
长方形的面积与长和宽有关。我们这学期学习了长方体和正方体,怎样求它们的体积呢?长方体的体积可能与什么有关呢?
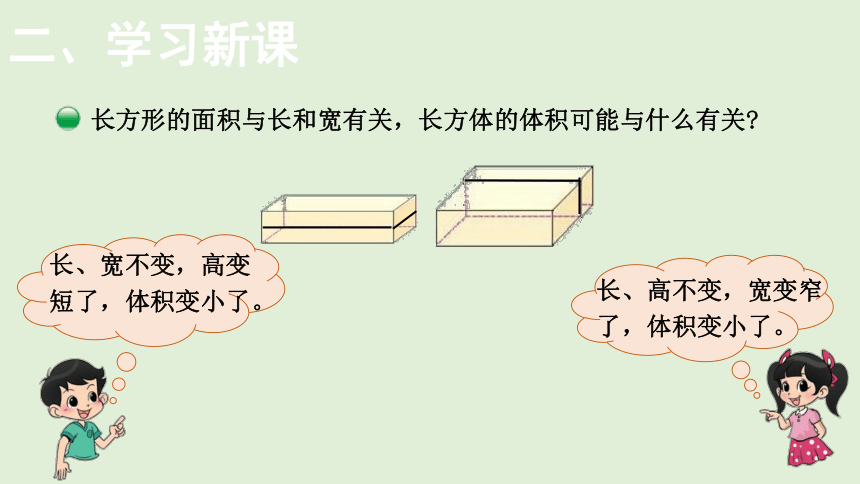
二、学习新课
长方形的面积与长和宽有关,长方体的体积可能与什么有关
长、宽不变,高变短了,体积变小了。
长、高不变,宽变窄了,体积变小了。
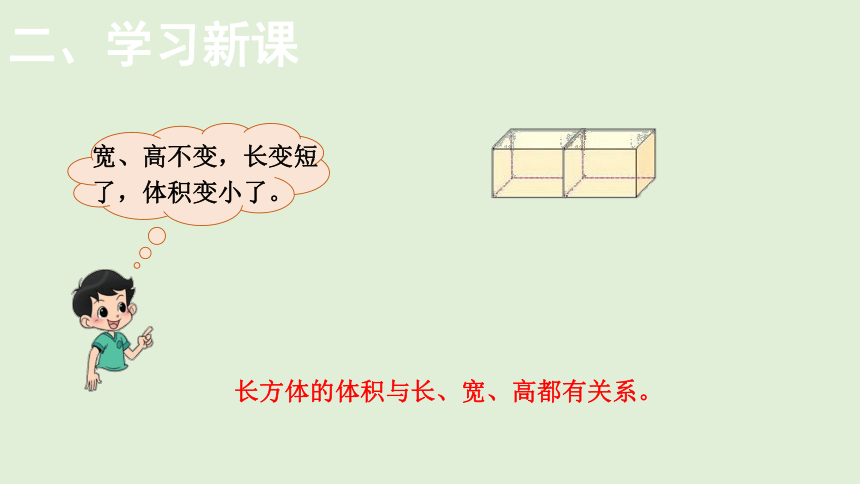
二、学习新课
宽、高不变,长变短了,体积变小了。
长方体的体积与长、宽、高都有关系。
二、学习新课
猜一猜,长方体的体积与长、宽、高有什么关系?
用一些相同的小正方体(棱长为1 cm)摆出3个不同的长方体,记录它们的长、宽、高,完成下表,验证你的猜想。
长/cm 宽/cm 高/cm 小正方体数量/个 体积/cm3
第1个长方体
第2个长方体
第3个长方体
二、学习新课
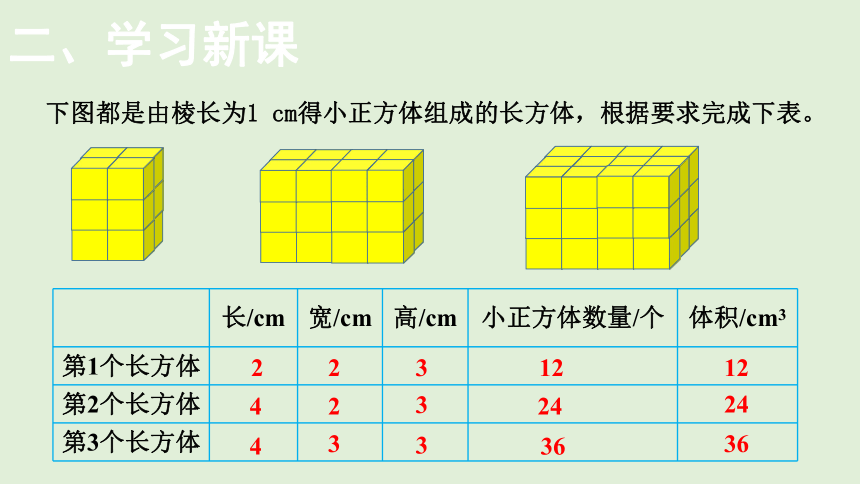
下图都是由棱长为1 cm得小正方体组成的长方体,根据要求完成下表。
长/cm 宽/cm 高/cm 小正方体数量/个 体积/cm3
第1个长方体
第2个长方体
第3个长方体
2
12
2
3
12
4
2
3
24
24
4
3
3
36
36
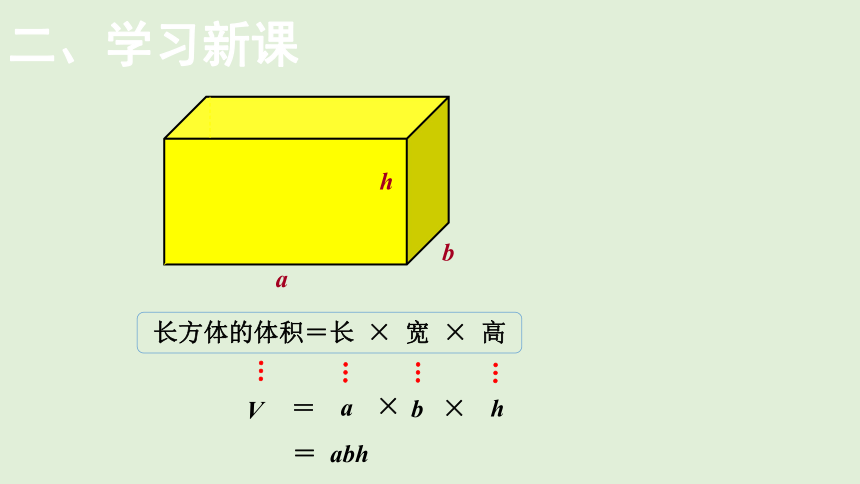
二、学习新课
h
a
b
长方体的体积=长 × 宽 × 高
…
…
…
…
=
×
×
= abh
a
b
h
V
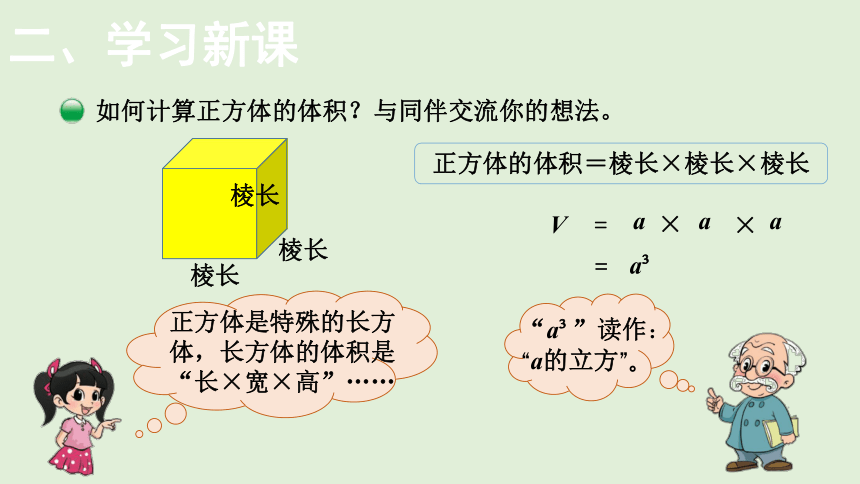
二、学习新课
如何计算正方体的体积?与同伴交流你的想法。
正方体的体积=棱长×棱长×棱长
=
×
×
=
V
a
a
a
a
棱长
棱长
棱长
正方体是特殊的长方体,长方体的体积是“长×宽×高”……
“a ”读作:“a的立方”。
二、学习新课
先算一算下列各图形的体积,再读一读,想一想。(单位:dm)
5×3×4=60 (dm3)
6×2×2=24 (dm3)
3×3×3=27 (dm3)
阴影部分的面积是上面各个图形底面的面积。
二、学习新课
长方体或正方体底面的面积叫底面积。
底面
底面
二、学习新课
长方体的体积=长×宽×高
V = Sh
h
a
b
底面积
正方体的体积=棱长×棱长×棱长
V = Sh
a
底面积
a
a
二、学习新课
二、学习新课
长方体(或正方体)的体积=底面积×高
底面
底面
V = Sh
二、学习新课
长方体 底面积 10 25 9
高/cm 8 6 7
体积/cm3 105 37.8
填一填。
80
150
15
4.2
三、巩固反馈
1.与同伴交流,我们是如何得到长方体、正方体的体积公式的?
略
三、巩固反馈
2.我说你做。
略
三、巩固反馈
3.用体积是1 cm3的小正方体摆成如下的图形,它们的体积各是多少?
3×2×2
=6×2
=12(cm3)
5×3×3
=15×3
=45(cm3)
2×2×2
=4×2
=8(cm3)
3×2×3
=6×3
=18(cm3)
三、巩固反馈
4.一块长方体形状的大理石,体积为30 m3,底面是面积为6 m2的
长方形,这块大理石的高是多少米?
30÷6=5(m)
答:这块大理石的高是5 m 。
三、巩固反馈
5.一个长方体水池,底面长12 dm,宽6 dm。如果要向这个池子里
注入2 dm高的水,需要多少升水?
12×6×2
=72×2
=144(dm3)
=144(升)
答:需要144升水。
三、巩固反馈
6.牙膏盒长15 cm,宽和高都是3 cm,现有一纸箱,内侧的尺寸
如图(单位:cm)。这个纸箱中最多能放多少盒牙膏?与
同伴交流,说一说你是怎样想的?
长可以摆(60÷15)盒,宽可以摆(30÷3)盒,高可以摆(30÷3)盒。
(60÷15)×(30÷3)×(30÷3)=400(盒)
答:这个纸箱中最多能放400盒牙膏。
7.将一个长8 cm、宽5 cm、高3 cm的长方体截成一个体积最大的正方体,这个正方体的体积是多少?结合下边的图想一想,再算一算。(单位:cm)
3×3×3=27(cm3)
答:这个正方体的体积是27 cm3。
三、巩固反馈
8.冷藏车厢的内部长3 m、宽2.2 m、高2 m,车厢内部的体积是
多少?
3×2.2×2=13.2(m3)
答:车厢内部的体积是13.2 m3 。
三、巩固反馈
9.实践活动。
⑴寻找生活中两个长方体形状的物体,先估一估它们的体积,再进行测量与计算。
⑵设计一个长方体盒子,使它能装下1000块长方体橡皮。
略
三、巩固反馈
四、课堂小结
1.长方体的体积=长 × 宽 × 高,用字母表示为
V=abh
2.正方体的体积=棱长×棱长×棱长,用字母表示为
V=a
3.长方体(正方体)的体积=底面积×高,用字母表
示为V=Sh
第3课时 长方体的体积
四 长方体(二)
一、复习引入
我们以前学习过长方形、正方形的面积公式,谁来说一说怎么计算长方形和正方形的面积呢?
一、复习引入
长方形的面积=长×宽
正方形的面积=边长×边长
长方形的面积与长和宽有关。我们这学期学习了长方体和正方体,怎样求它们的体积呢?长方体的体积可能与什么有关呢?
二、学习新课
长方形的面积与长和宽有关,长方体的体积可能与什么有关
长、宽不变,高变短了,体积变小了。
长、高不变,宽变窄了,体积变小了。
二、学习新课
宽、高不变,长变短了,体积变小了。
长方体的体积与长、宽、高都有关系。
二、学习新课
猜一猜,长方体的体积与长、宽、高有什么关系?
用一些相同的小正方体(棱长为1 cm)摆出3个不同的长方体,记录它们的长、宽、高,完成下表,验证你的猜想。
长/cm 宽/cm 高/cm 小正方体数量/个 体积/cm3
第1个长方体
第2个长方体
第3个长方体
二、学习新课
下图都是由棱长为1 cm得小正方体组成的长方体,根据要求完成下表。
长/cm 宽/cm 高/cm 小正方体数量/个 体积/cm3
第1个长方体
第2个长方体
第3个长方体
2
12
2
3
12
4
2
3
24
24
4
3
3
36
36
二、学习新课
h
a
b
长方体的体积=长 × 宽 × 高
…
…
…
…
=
×
×
= abh
a
b
h
V
二、学习新课
如何计算正方体的体积?与同伴交流你的想法。
正方体的体积=棱长×棱长×棱长
=
×
×
=
V
a
a
a
a
棱长
棱长
棱长
正方体是特殊的长方体,长方体的体积是“长×宽×高”……
“a ”读作:“a的立方”。
二、学习新课
先算一算下列各图形的体积,再读一读,想一想。(单位:dm)
5×3×4=60 (dm3)
6×2×2=24 (dm3)
3×3×3=27 (dm3)
阴影部分的面积是上面各个图形底面的面积。
二、学习新课
长方体或正方体底面的面积叫底面积。
底面
底面
二、学习新课
长方体的体积=长×宽×高
V = Sh
h
a
b
底面积
正方体的体积=棱长×棱长×棱长
V = Sh
a
底面积
a
a
二、学习新课
二、学习新课
长方体(或正方体)的体积=底面积×高
底面
底面
V = Sh
二、学习新课
长方体 底面积 10 25 9
高/cm 8 6 7
体积/cm3 105 37.8
填一填。
80
150
15
4.2
三、巩固反馈
1.与同伴交流,我们是如何得到长方体、正方体的体积公式的?
略
三、巩固反馈
2.我说你做。
略
三、巩固反馈
3.用体积是1 cm3的小正方体摆成如下的图形,它们的体积各是多少?
3×2×2
=6×2
=12(cm3)
5×3×3
=15×3
=45(cm3)
2×2×2
=4×2
=8(cm3)
3×2×3
=6×3
=18(cm3)
三、巩固反馈
4.一块长方体形状的大理石,体积为30 m3,底面是面积为6 m2的
长方形,这块大理石的高是多少米?
30÷6=5(m)
答:这块大理石的高是5 m 。
三、巩固反馈
5.一个长方体水池,底面长12 dm,宽6 dm。如果要向这个池子里
注入2 dm高的水,需要多少升水?
12×6×2
=72×2
=144(dm3)
=144(升)
答:需要144升水。
三、巩固反馈
6.牙膏盒长15 cm,宽和高都是3 cm,现有一纸箱,内侧的尺寸
如图(单位:cm)。这个纸箱中最多能放多少盒牙膏?与
同伴交流,说一说你是怎样想的?
长可以摆(60÷15)盒,宽可以摆(30÷3)盒,高可以摆(30÷3)盒。
(60÷15)×(30÷3)×(30÷3)=400(盒)
答:这个纸箱中最多能放400盒牙膏。
7.将一个长8 cm、宽5 cm、高3 cm的长方体截成一个体积最大的正方体,这个正方体的体积是多少?结合下边的图想一想,再算一算。(单位:cm)
3×3×3=27(cm3)
答:这个正方体的体积是27 cm3。
三、巩固反馈
8.冷藏车厢的内部长3 m、宽2.2 m、高2 m,车厢内部的体积是
多少?
3×2.2×2=13.2(m3)
答:车厢内部的体积是13.2 m3 。
三、巩固反馈
9.实践活动。
⑴寻找生活中两个长方体形状的物体,先估一估它们的体积,再进行测量与计算。
⑵设计一个长方体盒子,使它能装下1000块长方体橡皮。
略
三、巩固反馈
四、课堂小结
1.长方体的体积=长 × 宽 × 高,用字母表示为
V=abh
2.正方体的体积=棱长×棱长×棱长,用字母表示为
V=a
3.长方体(正方体)的体积=底面积×高,用字母表
示为V=Sh
