人教版七年级上册数学 第四章几何图形初步 小结复习(一)(共24张ppt)
文档属性
| 名称 | 人教版七年级上册数学 第四章几何图形初步 小结复习(一)(共24张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 367.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-26 20:51:11 | ||
图片预览




文档简介
(共24张PPT)
小结复习(一)
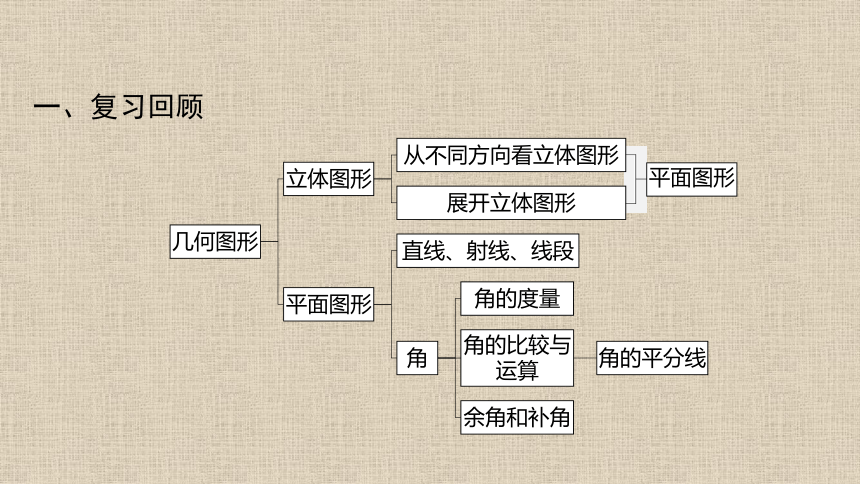
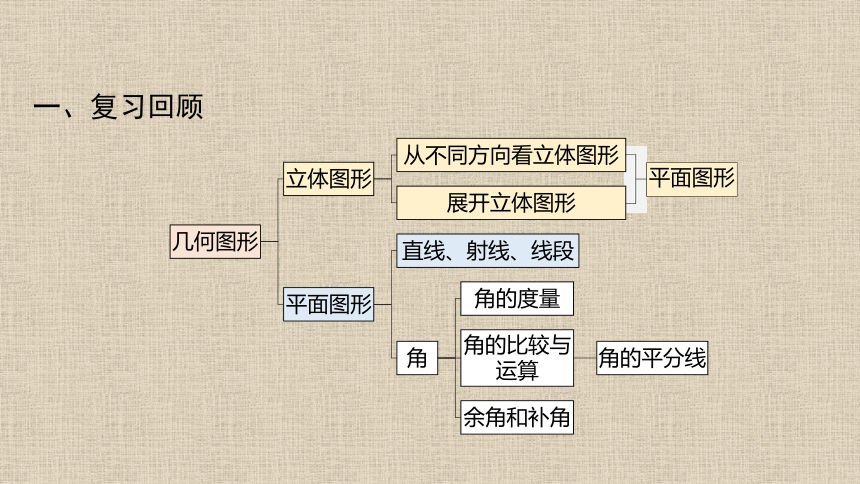
一、复习回顾
平面图形
一、复习回顾
平面图形
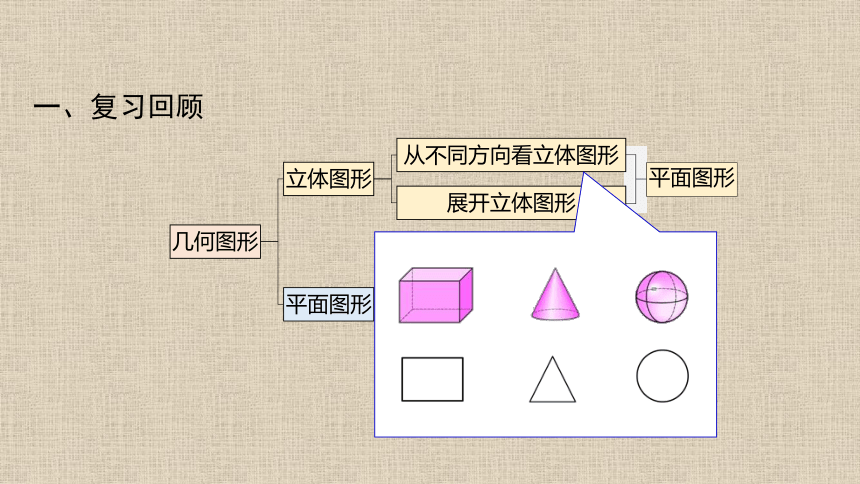
有些几何图形(如长方体、圆锥、圆柱、球等)的各部分不都在同一个平面内,它们是立体图形.
1. 立体图形
一、复习回顾
有些几何图形(如线段、角、三角形、长方形、圆等)的各部分都在同一个平面内,它们是平面图形.
2. 平面图形
一、复习回顾
平面图形
一、复习回顾
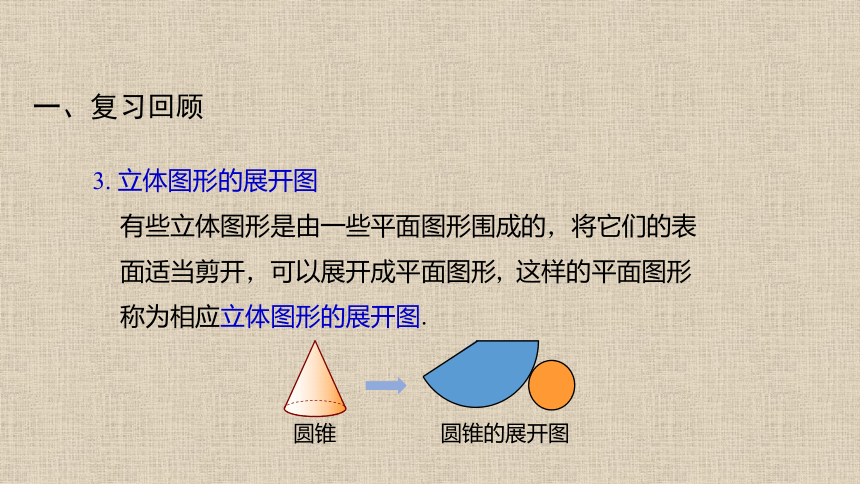
有些立体图形是由一些平面图形围成的,将它们的表面适当剪开,可以展开成平面图形, 这样的平面图形称为相应立体图形的展开图.
3. 立体图形的展开图
圆锥
圆锥的展开图
一、复习回顾
一、复习回顾
平面图形
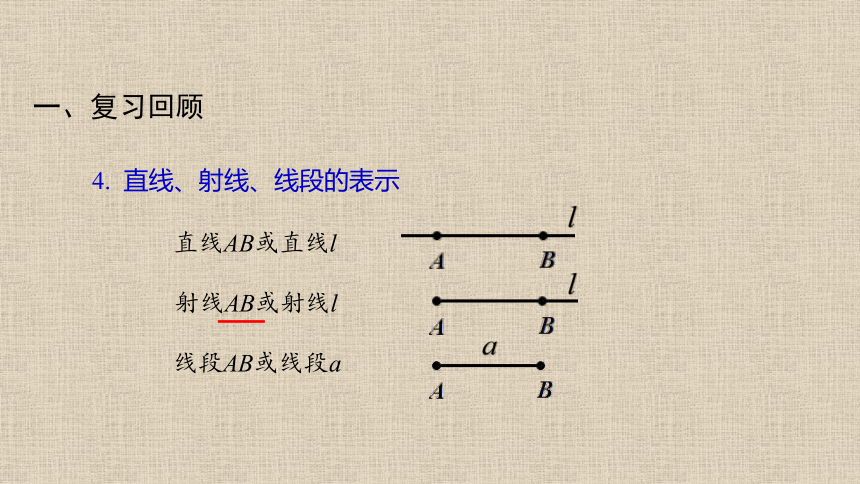
4. 直线、射线、线段的表示
一、复习回顾
直线AB或直线l
射线AB或射线l
线段AB或线段a
l
l
a
5. 线段的比较
刻度尺
一、复习回顾
AB>CD
AB=CD
AB6. 线段的和差
AC=AB+BC
AD=AB-BD
AB=AM+BM;
AM=AB-BM;
练习
BM=AB-AM.
一、复习回顾
所以AM=BM = AB.
因为点M是线段AB的中点,
因为AM=BM = AB,
所以点M是线段AB的中点.
7. 线段的中点
一、复习回顾
如图,把一条线段分成两条相等线段的点,叫做这条线段的中点.
例1 左下图是一块带有圆形空洞和长方形空洞的小木板,则下列物体中最有可能既可以堵住圆形空洞,又可以堵住长方形空洞的是( ).
二、典型例题
分析:
二、典型例题
例1 左下图是一块带有圆形空洞和长方形空洞的小木板,则下列物体中最有可能既可以堵住圆形空洞,又可以堵住长方形空洞的是( ).
二、典型例题
B
例2 (1)根据下列描述画出对应图形.
①点 A在直线l外;
二、典型例题
点和直线的位置关系
点B在直线l上;
交点
两条直线相交
二、典型例题
例2 (1)根据下列描述画出对应图形.
②直线 AB与直线CD相交于点 A;
例2 (2)如图,点A,B,C在同一条直线上,用恰当的语句描述点 A,B,C的位置关系.
点C在线段AB上;
或点B在线段AC的延长线上;
或点A在线段CB的反向延长线上.
二、典型例题
例3 (1)如图,建筑工人在砌墙时会在两个墙脚的位置分别插一根木桩,然后在木桩的相同高度处拉一条绳子,定出一条直的参照线,这样砌出的墙就是直的. 其道理是____________________.
两点确定一条直线
直线的基本事实
二、典型例题
例3 (2)如图,从A地到B地有不同的路线可以到达,其中____是最短的,理由是____________________.
线段的基本事实
两点之间,线段最短
③
二、典型例题
例4 如图,点C在线段AB上, AB=6,点M、点N分别是线段AC、BC的中点,求MN的长度.
分析:
点M是线段AC的中点
点N是线段BC的中点
二、典型例题
解:因为点M、点N分别是线段AC、BC的中点,
所以 , .
从而可得:
.
又因为AB=6,
所以 MN=3.
二、典型例题
例4 如图,点C在线段AB上, AB=6,点M、点N分别是线段AC、BC的中点,求MN的长度.
例4 如图,点C在线段AB上, AB=6,点M、点N分别是线段AC、BC的中点,求MN的长度.
直线AB
(2)点C在线段AB的反向延长线上
(3)点C在线段AB的延长线上
(1)点C在线段AB上
二、典型例题
1. 立体图形与平面图形的关系.
2. 直线、射线、线段:
(1)图形语言、文字语言和符号语言的相互转化;
(2)应用数学知识解释生活中的现象;
(3)简单的几何推理.
三、课堂小结
小结复习(一)
一、复习回顾
平面图形
一、复习回顾
平面图形
有些几何图形(如长方体、圆锥、圆柱、球等)的各部分不都在同一个平面内,它们是立体图形.
1. 立体图形
一、复习回顾
有些几何图形(如线段、角、三角形、长方形、圆等)的各部分都在同一个平面内,它们是平面图形.
2. 平面图形
一、复习回顾
平面图形
一、复习回顾
有些立体图形是由一些平面图形围成的,将它们的表面适当剪开,可以展开成平面图形, 这样的平面图形称为相应立体图形的展开图.
3. 立体图形的展开图
圆锥
圆锥的展开图
一、复习回顾
一、复习回顾
平面图形
4. 直线、射线、线段的表示
一、复习回顾
直线AB或直线l
射线AB或射线l
线段AB或线段a
l
l
a
5. 线段的比较
刻度尺
一、复习回顾
AB>CD
AB=CD
AB
AC=AB+BC
AD=AB-BD
AB=AM+BM;
AM=AB-BM;
练习
BM=AB-AM.
一、复习回顾
所以AM=BM = AB.
因为点M是线段AB的中点,
因为AM=BM = AB,
所以点M是线段AB的中点.
7. 线段的中点
一、复习回顾
如图,把一条线段分成两条相等线段的点,叫做这条线段的中点.
例1 左下图是一块带有圆形空洞和长方形空洞的小木板,则下列物体中最有可能既可以堵住圆形空洞,又可以堵住长方形空洞的是( ).
二、典型例题
分析:
二、典型例题
例1 左下图是一块带有圆形空洞和长方形空洞的小木板,则下列物体中最有可能既可以堵住圆形空洞,又可以堵住长方形空洞的是( ).
二、典型例题
B
例2 (1)根据下列描述画出对应图形.
①点 A在直线l外;
二、典型例题
点和直线的位置关系
点B在直线l上;
交点
两条直线相交
二、典型例题
例2 (1)根据下列描述画出对应图形.
②直线 AB与直线CD相交于点 A;
例2 (2)如图,点A,B,C在同一条直线上,用恰当的语句描述点 A,B,C的位置关系.
点C在线段AB上;
或点B在线段AC的延长线上;
或点A在线段CB的反向延长线上.
二、典型例题
例3 (1)如图,建筑工人在砌墙时会在两个墙脚的位置分别插一根木桩,然后在木桩的相同高度处拉一条绳子,定出一条直的参照线,这样砌出的墙就是直的. 其道理是____________________.
两点确定一条直线
直线的基本事实
二、典型例题
例3 (2)如图,从A地到B地有不同的路线可以到达,其中____是最短的,理由是____________________.
线段的基本事实
两点之间,线段最短
③
二、典型例题
例4 如图,点C在线段AB上, AB=6,点M、点N分别是线段AC、BC的中点,求MN的长度.
分析:
点M是线段AC的中点
点N是线段BC的中点
二、典型例题
解:因为点M、点N分别是线段AC、BC的中点,
所以 , .
从而可得:
.
又因为AB=6,
所以 MN=3.
二、典型例题
例4 如图,点C在线段AB上, AB=6,点M、点N分别是线段AC、BC的中点,求MN的长度.
例4 如图,点C在线段AB上, AB=6,点M、点N分别是线段AC、BC的中点,求MN的长度.
直线AB
(2)点C在线段AB的反向延长线上
(3)点C在线段AB的延长线上
(1)点C在线段AB上
二、典型例题
1. 立体图形与平面图形的关系.
2. 直线、射线、线段:
(1)图形语言、文字语言和符号语言的相互转化;
(2)应用数学知识解释生活中的现象;
(3)简单的几何推理.
三、课堂小结
