人教版七年级上册数学 第四章几何图形初步小结复习(二)(共23张ppt)
文档属性
| 名称 | 人教版七年级上册数学 第四章几何图形初步小结复习(二)(共23张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 321.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-26 00:00:00 | ||
图片预览




文档简介
(共23张PPT)
小结复习(二)
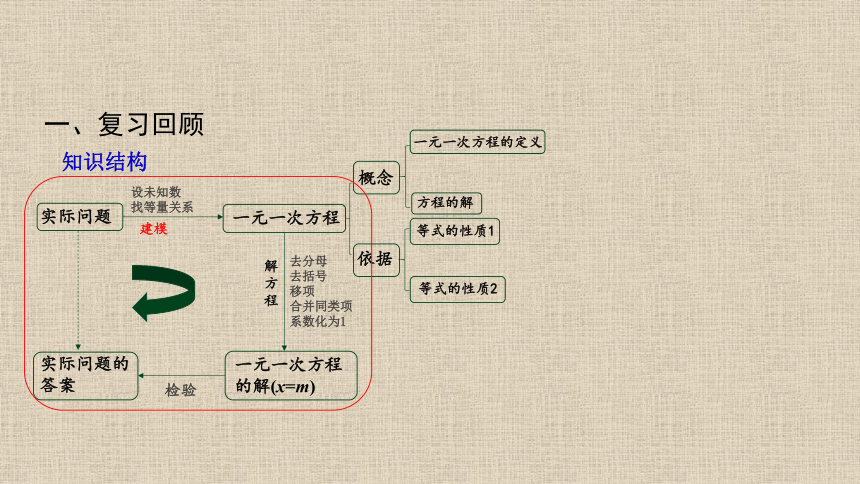
知识结构
一、复习回顾
概念
依据
方程的解
等式的性质1
等式的性质2
去分母
去括号
移项
合并同类项
系数化为1
设未知数
找等量关系
一元一次方程的定义
一元一次方程
的解(x=m)
实际问题的答案
检验
实际问题
一元一次方程
建模
解方程
二、典型例题
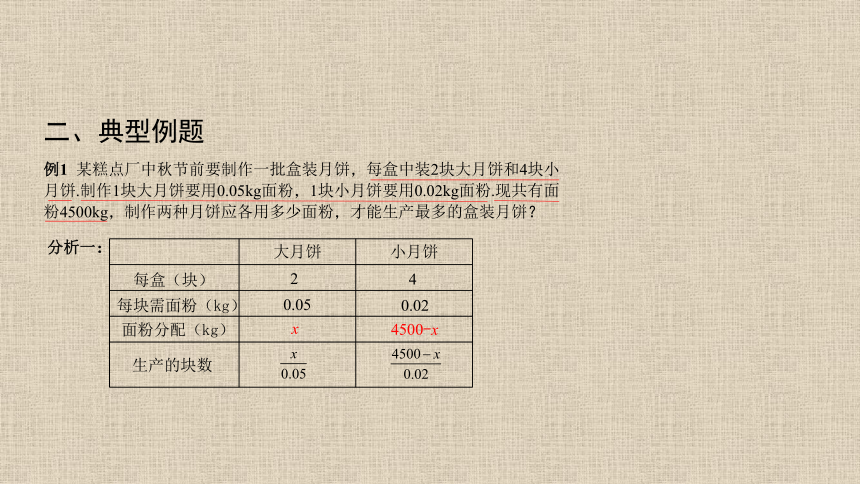
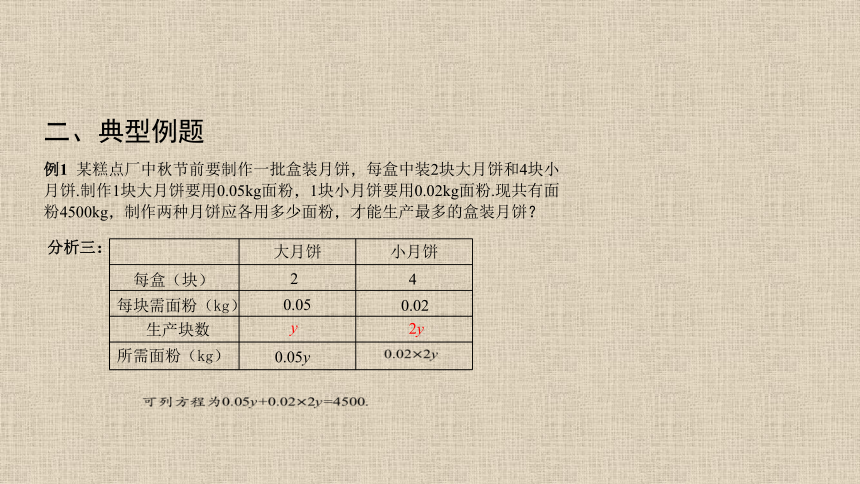
例1 某糕点厂中秋节前要制作一批盒装月饼,每盒中装2块大月饼和4块小月饼.制作1块大月饼要用0.05kg面粉,1块小月饼要用0.02kg面粉.现共有面粉4500kg,制作两种月饼应各用多少面粉,才能生产最多的盒装月饼?
二、典型例题
大月饼 小月饼
分析一:
每盒(块)
2
4
0.05
0.02
每块需面粉(kg)
面粉分配(kg)
x
4500-x
生产的块数
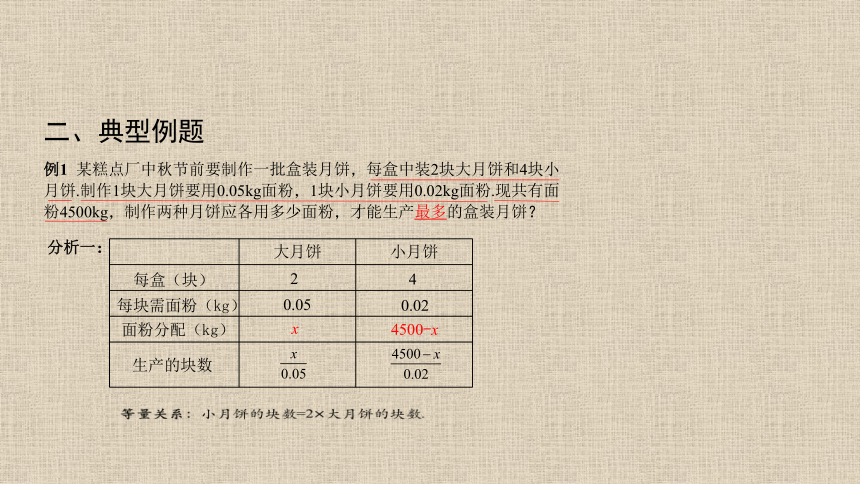
例1 某糕点厂中秋节前要制作一批盒装月饼,每盒中装2块大月饼和4块小月饼.制作1块大月饼要用0.05kg面粉,1块小月饼要用0.02kg面粉.现共有面粉4500kg,制作两种月饼应各用多少面粉,才能生产最多的盒装月饼?
二、典型例题
大月饼 小月饼
分析一:
每盒(块)
2
4
0.05
0.02
每块需面粉(kg)
面粉分配(kg)
x
4500-x
生产的块数
等量关系:小月饼的块数=2大月饼的块数.
例1 某糕点厂中秋节前要制作一批盒装月饼,每盒中装2块大月饼和4块小月饼.制作1块大月饼要用0.05kg面粉,1块小月饼要用0.02kg面粉.现共有面粉4500kg,制作两种月饼应各用多少面粉,才能生产最多的盒装月饼?
二、典型例题
解:设用xkg面粉生产大月饼,则用(4500-x)kg面粉生产小月饼.
解方程得
4500-x=2000.
检验: x=2500是原方程的解且符合实际意义.
答:用2500kg面粉生产大月饼,用2000kg面粉生产小月饼,能生产最多的盒装月饼.
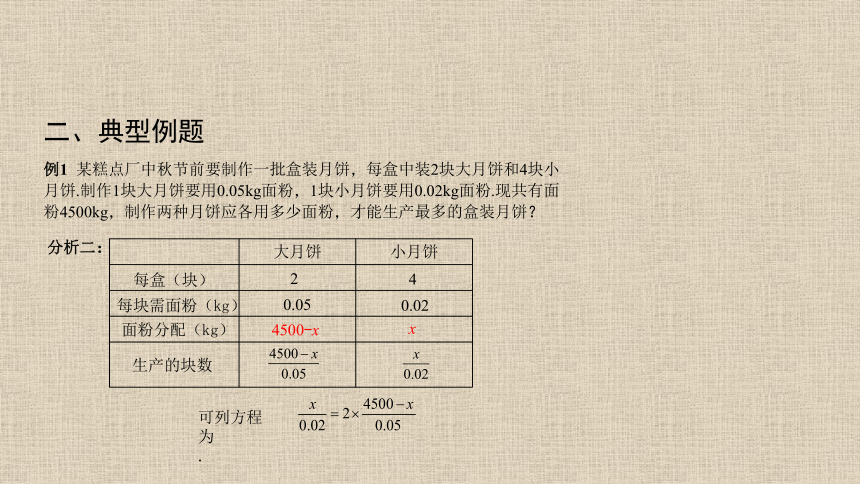
例1 某糕点厂中秋节前要制作一批盒装月饼,每盒中装2块大月饼和4块小月饼.制作1块大月饼要用0.05kg面粉,1块小月饼要用0.02kg面粉.现共有面粉4500kg,制作两种月饼应各用多少面粉,才能生产最多的盒装月饼?
x=2500.
二、典型例题
大月饼 小月饼
每盒(块)
2
4
0.05
0.02
每块需面粉(kg)
面粉分配(kg)
x
4500-x
生产的块数
分析二:
可列方程为 .
例1 某糕点厂中秋节前要制作一批盒装月饼,每盒中装2块大月饼和4块小月饼.制作1块大月饼要用0.05kg面粉,1块小月饼要用0.02kg面粉.现共有面粉4500kg,制作两种月饼应各用多少面粉,才能生产最多的盒装月饼?
二、典型例题
大月饼 小月饼
每盒(块)
2
4
0.05
0.02
每块需面粉(kg)
生产块数
2y
y
所需面粉(kg)
分析三:
可列方程为0.05y+0.022y=4500.
0.05y
0.022y
例1 某糕点厂中秋节前要制作一批盒装月饼,每盒中装2块大月饼和4块小月饼.制作1块大月饼要用0.05kg面粉,1块小月饼要用0.02kg面粉.现共有面粉4500kg,制作两种月饼应各用多少面粉,才能生产最多的盒装月饼?
二、典型例题
解:设生产y块大月饼,则生产2y块小月饼.
0.05y+0.022y=4500.
0.09y=4500.
y=50000.
0.05y=2500.
0.022y=2000.
答:用2500kg面粉生产大月饼,用2000kg面粉生产小月饼,能生产最多的盒装月饼.
二、典型例题
例2 为了备战学校体育节的乒乓球比赛活动,某班计划买5副乒乓球拍和若干盒乒乓球(多于5盒),该班体育委员发现在学校附近有甲、乙两家商店都在出售相同品牌的乒乓球拍和乒乓球,乒乓球拍每副售价100元,乒乓球每盒售价25元,经过体育委员的洽谈,甲商店给出每买一副乒乓球拍送一盒乒乓球的优惠;乙商店给出乒乓球拍和乒乓球全部九折的优惠.
乒乓球拍 乒乓球
数量 5副 若干(超过5盒)
单价
100元
25元
分析:某班计划购买
二、典型例题
例2 为了备战学校体育节的乒乓球比赛活动,某班计划买5副乒乓球拍和若干盒乒乓球(多于5盒),该班体育委员发现在学校附近有甲、乙两家商店都在出售相同品牌的乒乓球拍和乒乓球,乒乓球拍每副售价100元,乒乓球每盒售价25元,经过体育委员的洽谈,甲商店给出每买一副乒乓球拍送一盒乒乓球的优惠;乙商店给出乒乓球拍和乒乓球全部九折的优惠.
分析:商店优惠方式
甲商店:一副乒乓球拍送一盒乒乓球;
乙商店:乒乓球拍和乒乓球全部九折.
二、典型例题
(1)若这个班计划购买6盒乒乓球,则在甲商店付款_____元,
在乙商店付款_____元;
解:在甲商店付款5副乒乓球拍的价钱+(6-5)盒乒乓球的价钱
在乙商店付款5副乒乓球拍的价钱+6盒乒乓球的价钱)0.9
=5100+25=525(元),
= (5100+625)0.9=585 (元).
525
585
乒乓球拍 乒乓球
数量 5副
甲商店:一副乒乓球拍送一盒乒乓球;
乙商店:乒乓球拍和乒乓球全部九折.
分析:某班计划购买
商店优惠方式
100元
25元
6盒
单价
二、典型例题
(2)这个班购买多少盒乒乓球时,在甲、乙两商店付款相同?并求出此时需付款多少元?
在甲商店付款= 5副乒乓球拍的价钱+(x -5)盒乒乓球的价钱
在乙商店付款= (5副乒乓球拍的价钱+ x盒乒乓球的价钱)0.9
=5100+25(x-5) ,
= (5100+25x)0.9.
等量关系:在甲商店付款数目=在乙商店付款数目.
乒乓球拍 乒乓球
数量 5副
单价
100元
25元
甲商店:一副乒乓球拍送一盒乒乓球;
乙商店:乒乓球拍和乒乓球全部九折.
分析:某班计划购买
商店优惠方式
x盒
二、典型例题
解:设购买x 盒乒乓球时,在甲、乙两商店付款相同.
解方程,得
x=30.
(检验:x=30是原方程的解,且符合实际情况.)
答:购买30盒乒乓球时,在甲、乙两商店付款相同.
此时需要付款1125元.
5100+25(x-5)=(5100+25x)0.9 .
(2)这个班购买多少盒乒乓球时,在甲、乙两商店付款相同?并求出此时需付款多少元?
5100+25(30-5)=1125(元)
二、典型例题
(3)若这个班购买乒乓球的数量暂时未定,选择哪家商店购买更合算?
同学们能给出建议吗?
分析:
在甲商店付款=5100+25(x-5) =375+25x,
在乙商店付款= (5100+25x)0.9=450+22.5x.
若甲商店付款-乙商店付款>0,则选择在乙商店购买;
若甲商店付款-乙商店付款=0,则选择甲、乙商店均可;
若甲商店付款-乙商店付款<0,则选择在甲商店购买.
通过作差比较大小.
二、典型例题
(3)若这个班购买乒乓球的数量暂时未定,选择哪家商店购买更合算?
同学们能给出建议吗?
分析:
在甲商店付款数-在乙商店付款数= 375+25x-(450+22.5x),
= 375+25x-450-22.5x,
= 2.5x-75.
当x=30时, 2.5x-75=0,在甲商店付款数=在乙商店付款数;
当x>30时, 2.5x-75>0,在甲商店付款数>在乙商店付款数;
当x<30时, 2.5x-75<0, 在甲商店付款数<在乙商店付款数.
二、典型例题
(3)若这个班购买乒乓球的数量暂时未定,选择哪家商店购买更合算?
同学们能给出建议吗?
当购买少于30盒乒乓球时,选择在甲商店购买;
当购买多于30盒乒乓球时,选择在乙商店购买;
当购买30盒乒乓球时,选择甲、乙商店均可.
答:
二、典型例题
分析:
由(1)若购买6盒乒乓球,在甲商店付款525元,在乙商店付款585元,
因为525<585,所以当购买5副乒乓球拍和6盒乒乓球时选择甲商店.
思考:你能否通过比较甲、乙两家商店“购买6盒乒乓球”的付款数来决定当“购买少于30盒乒乓球”时选择在哪家商店购买;同样地,能否通过比较甲、乙两家商店“购买31盒乒乓球”的付款数来决定当“购买多于30盒乒乓球”时选择在哪家商店购买?
二、典型例题
购买5副乒乓球拍和31盒乒乓球时甲商店付款:
5副乒乓球拍的价钱+(31-5)盒乒乓球的价钱
=5100+2625=1150(元).
或 购买5副乒乓球拍的价钱和乒乓球30盒时的价钱+1盒乒乓球的价钱
=1125+25=1150 (元).
分析:
二、典型例题
购买5副乒乓球拍和31盒乒乓球时乙商店付款:
分析:
(5副乒乓球拍的价钱+31盒乒乓球的价钱)0.9
=(5100+3125) 0.9=1147.5(元).
或 5副乒乓球拍的价钱购买乒乓球30盒时的价钱+1盒乒乓球的价钱0.9
=1125+250.9=1147.5 (元).
因为1147.5<1150,所以当购买31盒乒乓球时选择乙商店.
二、典型例题
乒乓球拍 乒乓球
数量 5副
单价
100元
25元
甲商店:一副乒乓球拍送一盒乒乓球;
乙商店:乒乓球拍和乒乓球全部九折.
商店优惠方式
x盒
分析:某班计划购买
甲商店优惠=5盒乒乓球的价格=125元
乙商店优惠= 原价-0.9原价= 0.1原价
三、课堂小结
设未知数
找等量关系
一元一次方程
的解(x=m)
实际问题的答案
检验
实际问题
一元一次方程
建模
解方程
三、课堂小结
设未知数
找等量关系
一元一次方程
的解(x=m)
实际问题的答案
检验
实际问题
一元一次方程
建模
解方程
小结复习(二)
知识结构
一、复习回顾
概念
依据
方程的解
等式的性质1
等式的性质2
去分母
去括号
移项
合并同类项
系数化为1
设未知数
找等量关系
一元一次方程的定义
一元一次方程
的解(x=m)
实际问题的答案
检验
实际问题
一元一次方程
建模
解方程
二、典型例题
例1 某糕点厂中秋节前要制作一批盒装月饼,每盒中装2块大月饼和4块小月饼.制作1块大月饼要用0.05kg面粉,1块小月饼要用0.02kg面粉.现共有面粉4500kg,制作两种月饼应各用多少面粉,才能生产最多的盒装月饼?
二、典型例题
大月饼 小月饼
分析一:
每盒(块)
2
4
0.05
0.02
每块需面粉(kg)
面粉分配(kg)
x
4500-x
生产的块数
例1 某糕点厂中秋节前要制作一批盒装月饼,每盒中装2块大月饼和4块小月饼.制作1块大月饼要用0.05kg面粉,1块小月饼要用0.02kg面粉.现共有面粉4500kg,制作两种月饼应各用多少面粉,才能生产最多的盒装月饼?
二、典型例题
大月饼 小月饼
分析一:
每盒(块)
2
4
0.05
0.02
每块需面粉(kg)
面粉分配(kg)
x
4500-x
生产的块数
等量关系:小月饼的块数=2大月饼的块数.
例1 某糕点厂中秋节前要制作一批盒装月饼,每盒中装2块大月饼和4块小月饼.制作1块大月饼要用0.05kg面粉,1块小月饼要用0.02kg面粉.现共有面粉4500kg,制作两种月饼应各用多少面粉,才能生产最多的盒装月饼?
二、典型例题
解:设用xkg面粉生产大月饼,则用(4500-x)kg面粉生产小月饼.
解方程得
4500-x=2000.
检验: x=2500是原方程的解且符合实际意义.
答:用2500kg面粉生产大月饼,用2000kg面粉生产小月饼,能生产最多的盒装月饼.
例1 某糕点厂中秋节前要制作一批盒装月饼,每盒中装2块大月饼和4块小月饼.制作1块大月饼要用0.05kg面粉,1块小月饼要用0.02kg面粉.现共有面粉4500kg,制作两种月饼应各用多少面粉,才能生产最多的盒装月饼?
x=2500.
二、典型例题
大月饼 小月饼
每盒(块)
2
4
0.05
0.02
每块需面粉(kg)
面粉分配(kg)
x
4500-x
生产的块数
分析二:
可列方程为 .
例1 某糕点厂中秋节前要制作一批盒装月饼,每盒中装2块大月饼和4块小月饼.制作1块大月饼要用0.05kg面粉,1块小月饼要用0.02kg面粉.现共有面粉4500kg,制作两种月饼应各用多少面粉,才能生产最多的盒装月饼?
二、典型例题
大月饼 小月饼
每盒(块)
2
4
0.05
0.02
每块需面粉(kg)
生产块数
2y
y
所需面粉(kg)
分析三:
可列方程为0.05y+0.022y=4500.
0.05y
0.022y
例1 某糕点厂中秋节前要制作一批盒装月饼,每盒中装2块大月饼和4块小月饼.制作1块大月饼要用0.05kg面粉,1块小月饼要用0.02kg面粉.现共有面粉4500kg,制作两种月饼应各用多少面粉,才能生产最多的盒装月饼?
二、典型例题
解:设生产y块大月饼,则生产2y块小月饼.
0.05y+0.022y=4500.
0.09y=4500.
y=50000.
0.05y=2500.
0.022y=2000.
答:用2500kg面粉生产大月饼,用2000kg面粉生产小月饼,能生产最多的盒装月饼.
二、典型例题
例2 为了备战学校体育节的乒乓球比赛活动,某班计划买5副乒乓球拍和若干盒乒乓球(多于5盒),该班体育委员发现在学校附近有甲、乙两家商店都在出售相同品牌的乒乓球拍和乒乓球,乒乓球拍每副售价100元,乒乓球每盒售价25元,经过体育委员的洽谈,甲商店给出每买一副乒乓球拍送一盒乒乓球的优惠;乙商店给出乒乓球拍和乒乓球全部九折的优惠.
乒乓球拍 乒乓球
数量 5副 若干(超过5盒)
单价
100元
25元
分析:某班计划购买
二、典型例题
例2 为了备战学校体育节的乒乓球比赛活动,某班计划买5副乒乓球拍和若干盒乒乓球(多于5盒),该班体育委员发现在学校附近有甲、乙两家商店都在出售相同品牌的乒乓球拍和乒乓球,乒乓球拍每副售价100元,乒乓球每盒售价25元,经过体育委员的洽谈,甲商店给出每买一副乒乓球拍送一盒乒乓球的优惠;乙商店给出乒乓球拍和乒乓球全部九折的优惠.
分析:商店优惠方式
甲商店:一副乒乓球拍送一盒乒乓球;
乙商店:乒乓球拍和乒乓球全部九折.
二、典型例题
(1)若这个班计划购买6盒乒乓球,则在甲商店付款_____元,
在乙商店付款_____元;
解:在甲商店付款5副乒乓球拍的价钱+(6-5)盒乒乓球的价钱
在乙商店付款5副乒乓球拍的价钱+6盒乒乓球的价钱)0.9
=5100+25=525(元),
= (5100+625)0.9=585 (元).
525
585
乒乓球拍 乒乓球
数量 5副
甲商店:一副乒乓球拍送一盒乒乓球;
乙商店:乒乓球拍和乒乓球全部九折.
分析:某班计划购买
商店优惠方式
100元
25元
6盒
单价
二、典型例题
(2)这个班购买多少盒乒乓球时,在甲、乙两商店付款相同?并求出此时需付款多少元?
在甲商店付款= 5副乒乓球拍的价钱+(x -5)盒乒乓球的价钱
在乙商店付款= (5副乒乓球拍的价钱+ x盒乒乓球的价钱)0.9
=5100+25(x-5) ,
= (5100+25x)0.9.
等量关系:在甲商店付款数目=在乙商店付款数目.
乒乓球拍 乒乓球
数量 5副
单价
100元
25元
甲商店:一副乒乓球拍送一盒乒乓球;
乙商店:乒乓球拍和乒乓球全部九折.
分析:某班计划购买
商店优惠方式
x盒
二、典型例题
解:设购买x 盒乒乓球时,在甲、乙两商店付款相同.
解方程,得
x=30.
(检验:x=30是原方程的解,且符合实际情况.)
答:购买30盒乒乓球时,在甲、乙两商店付款相同.
此时需要付款1125元.
5100+25(x-5)=(5100+25x)0.9 .
(2)这个班购买多少盒乒乓球时,在甲、乙两商店付款相同?并求出此时需付款多少元?
5100+25(30-5)=1125(元)
二、典型例题
(3)若这个班购买乒乓球的数量暂时未定,选择哪家商店购买更合算?
同学们能给出建议吗?
分析:
在甲商店付款=5100+25(x-5) =375+25x,
在乙商店付款= (5100+25x)0.9=450+22.5x.
若甲商店付款-乙商店付款>0,则选择在乙商店购买;
若甲商店付款-乙商店付款=0,则选择甲、乙商店均可;
若甲商店付款-乙商店付款<0,则选择在甲商店购买.
通过作差比较大小.
二、典型例题
(3)若这个班购买乒乓球的数量暂时未定,选择哪家商店购买更合算?
同学们能给出建议吗?
分析:
在甲商店付款数-在乙商店付款数= 375+25x-(450+22.5x),
= 375+25x-450-22.5x,
= 2.5x-75.
当x=30时, 2.5x-75=0,在甲商店付款数=在乙商店付款数;
当x>30时, 2.5x-75>0,在甲商店付款数>在乙商店付款数;
当x<30时, 2.5x-75<0, 在甲商店付款数<在乙商店付款数.
二、典型例题
(3)若这个班购买乒乓球的数量暂时未定,选择哪家商店购买更合算?
同学们能给出建议吗?
当购买少于30盒乒乓球时,选择在甲商店购买;
当购买多于30盒乒乓球时,选择在乙商店购买;
当购买30盒乒乓球时,选择甲、乙商店均可.
答:
二、典型例题
分析:
由(1)若购买6盒乒乓球,在甲商店付款525元,在乙商店付款585元,
因为525<585,所以当购买5副乒乓球拍和6盒乒乓球时选择甲商店.
思考:你能否通过比较甲、乙两家商店“购买6盒乒乓球”的付款数来决定当“购买少于30盒乒乓球”时选择在哪家商店购买;同样地,能否通过比较甲、乙两家商店“购买31盒乒乓球”的付款数来决定当“购买多于30盒乒乓球”时选择在哪家商店购买?
二、典型例题
购买5副乒乓球拍和31盒乒乓球时甲商店付款:
5副乒乓球拍的价钱+(31-5)盒乒乓球的价钱
=5100+2625=1150(元).
或 购买5副乒乓球拍的价钱和乒乓球30盒时的价钱+1盒乒乓球的价钱
=1125+25=1150 (元).
分析:
二、典型例题
购买5副乒乓球拍和31盒乒乓球时乙商店付款:
分析:
(5副乒乓球拍的价钱+31盒乒乓球的价钱)0.9
=(5100+3125) 0.9=1147.5(元).
或 5副乒乓球拍的价钱购买乒乓球30盒时的价钱+1盒乒乓球的价钱0.9
=1125+250.9=1147.5 (元).
因为1147.5<1150,所以当购买31盒乒乓球时选择乙商店.
二、典型例题
乒乓球拍 乒乓球
数量 5副
单价
100元
25元
甲商店:一副乒乓球拍送一盒乒乓球;
乙商店:乒乓球拍和乒乓球全部九折.
商店优惠方式
x盒
分析:某班计划购买
甲商店优惠=5盒乒乓球的价格=125元
乙商店优惠= 原价-0.9原价= 0.1原价
三、课堂小结
设未知数
找等量关系
一元一次方程
的解(x=m)
实际问题的答案
检验
实际问题
一元一次方程
建模
解方程
三、课堂小结
设未知数
找等量关系
一元一次方程
的解(x=m)
实际问题的答案
检验
实际问题
一元一次方程
建模
解方程
