人教版八年级数学上册乘法公式 期末复习训练 (word版含解析)
文档属性
| 名称 | 人教版八年级数学上册乘法公式 期末复习训练 (word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 178.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-27 07:36:11 | ||
图片预览




文档简介
2021-2022学年人教版八年级数学上册《乘法公式》期末综合知识点分类训练(附答案)
一.完全平方公式
1.已知a+b=5,ab=3,则a2+b2的值是 .
2.若x﹣y=3,xy=1,则x2+y2= .
3.已知a+b=5,ab=3,则a2+b2= .
4.我国宋朝数学家杨辉在他的著作《详解九章算法》中提出“杨辉三角”(如图),此图揭示了(a+b)n(n为非负整数)展开式的项数及各项系数的有关规律.
例如:(a+b)0=1,它只有一项,系数为1;系数和为1;
(a+b)1=a+b,它有两项,系数分别为1,1,系数和为2;
(a+b)2=a2+2ab+b2,它有三项,系数分别为1,2,1,系数和为4;
(a+b)3=a3+3a2b+3ab2+b3,它有四项,系数分别为1,3,3,1,系数和为8;…,
则(a+b)n的展开式共有 项,系数和为 .
5.已知(2028﹣a)2+(2027﹣a)2=1,则(2028﹣a) (2027﹣a)= .
6.已知a+b=5,ab=3,则a﹣b= .
7.若(a+b)2=16,(a﹣b)2=14,则代数式a2+b2的值为 .
8.定义=ad﹣bc,上述记号就叫做2阶行列式.若=6,x= .
9.如果x2﹣4x+1=0,那么= .
10.已知实数m,n满足m+n=6,mn=﹣3.
(1)求(m﹣2)(n﹣2)的值;
(2)求m2+n2的值.
11.已知a+b=3,ab=2,求a2+b2,(a﹣b)2的值.
12.已知:x+y=6,xy=4,求下列各式的值
(1)x2+y2
(2)(x﹣y)2.
13.已知:(x+y)2=6,(x﹣y)2=2,试求:
(1)x2+y2的值;
(2)xy的值.
14.已知a+b=3,ab=﹣4,求a2﹣ab+b2的值.
15.已知x+=4,求x﹣的值.
16.下表为杨辉三角系数表的一部分,它的作用是指导读者按规律写出形如:
(a+b)n(n为正整数)展开式的系数,请你仔细观察下表中的规律,填出(a+b)4展开式中所缺的系数.
(a+b)=a+b
(a+b)2=a2+2ab+b2
(a+b)3=a3+3a2b+3ab2+b3
(a+b)4=a4+ a3b+ a2b2+ ab3+b4.
17.我国宋代数学家杨辉写了一本书《详解九章算术》.书中记载了一个用数字排成的三角形我们叫作杨辉三角形
(a+b)0=1…1
(a+b)1=a+b…1 1
(a+b)2=a2+2ab+b2…1 2 1
(a+b)3=a3+3a2b+3ab2+b3…1 3 3 1
(a+b)4=a4+4a3b+6a2b2+4ab3+b4… 1 4 6 4 1
(1)请写出第五行的数字 ;
(2)第n行杨辉三角形数字与(a+b)n的展开结果关系如上图所示,请写出(a+b)5的展开结果;
(3)已知(a﹣b)1=a﹣b,(a﹣b)2=a2﹣2ab+b2,(a﹣b)3=a3﹣3a2b+3ab2﹣b3(a﹣b)4=a4﹣4a3b+6a2b2﹣4ab3+b4.请写出(a﹣b)5的展开结果.
二.完全平方公式的几何背景
18.如图,两个正方形边长分别为a,b,如果a+b=10,ab=18,则阴影部分的面积为 .
19.用4块完全相同的长方形拼成正方形(如图),用不同的方法,计算图中阴影部分的面积,可得到1个关于a,b的等式为 .
20.利用一个a×a的正方形,4个b×b的正方形,4个a×b的长方形,可拼成一个无缝隙且不重叠的大正方形,则这个大正方形的边长是 .
21.请认真观察图形,解答下列问题:
(1)根据图中条件,用两种方法表示两个阴影图形的面积的和(只需表示,不必化简);并由此得到怎样的等量关系?请用等式表示;
(2)如果图中的a,b(a>b)满足a2+b2=53,ab=14,
求:①a+b的值; ②a﹣b的值.
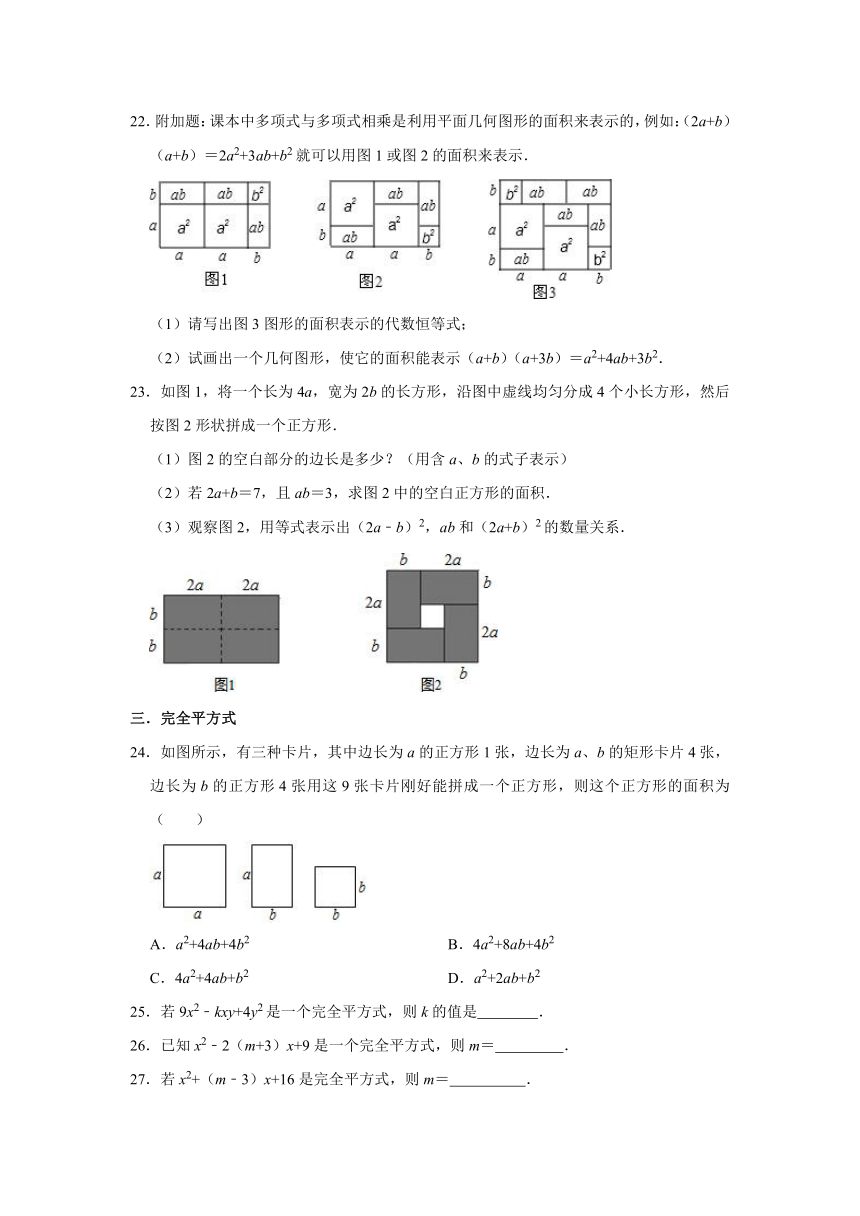
22.附加题:课本中多项式与多项式相乘是利用平面几何图形的面积来表示的,例如:(2a+b)(a+b)=2a2+3ab+b2就可以用图1或图2的面积来表示.
(1)请写出图3图形的面积表示的代数恒等式;
(2)试画出一个几何图形,使它的面积能表示(a+b)(a+3b)=a2+4ab+3b2.
23.如图1,将一个长为4a,宽为2b的长方形,沿图中虚线均匀分成4个小长方形,然后按图2形状拼成一个正方形.
(1)图2的空白部分的边长是多少?(用含a、b的式子表示)
(2)若2a+b=7,且ab=3,求图2中的空白正方形的面积.
(3)观察图2,用等式表示出(2a﹣b)2,ab和(2a+b)2的数量关系.
三.完全平方式
24.如图所示,有三种卡片,其中边长为a的正方形1张,边长为a、b的矩形卡片4张,边长为b的正方形4张用这9张卡片刚好能拼成一个正方形,则这个正方形的面积为( )
A.a2+4ab+4b2 B.4a2+8ab+4b2
C.4a2+4ab+b2 D.a2+2ab+b2
25.若9x2﹣kxy+4y2是一个完全平方式,则k的值是 .
26.已知x2﹣2(m+3)x+9是一个完全平方式,则m= .
27.若x2+(m﹣3)x+16是完全平方式,则m= .
28.已知x2+mx+9是完全平方式,则常数m等于 .
四.平方差公式
29.计算并观察、探究下列式子
①(x﹣1)(x+1)=
②(x﹣1)(x2+x+1)=
③(x﹣1)(x3+x2+x+1)=x4﹣1
④(x﹣1)(x4+x3+x2+x+1)=x5﹣1
⑤(x﹣1)(x5+x4+x3+x2+x+1)=x6﹣1
…
由以上规律
(1)填空:(x﹣1)(xn+xn﹣1+…+x+1)= .
(2)求:22022+22021+22020+…+22+2+1 的值.
五.平方差公式的几何背景
30.乘法公式的探究及应用.
(1)如图1,可以求出阴影部分的面积是 (写成两数平方差的形式);
(2)如图2,若将阴影部分裁剪下来,重新拼成一个长方形,它的宽是 ,长是 ,面积是 .(写成多项式乘法的形式)
(3)比较左、右两图的阴影部分面积,可以得到乘法公式 .(用式子表达)
(4)运用你所得到的公式,计算下列各题:
①10.3×9.7
②(2m+n﹣p)(2m﹣n+p)
31.如图1所示,边长为a的正方形中有一个边长为b的小正方形,如图2所示是由图1中阴影部分拼成的一个长方形.
(1)设图1中阴影部分面积为S1,图2中阴影部分面积为S2.请直接用含a,b的代数式表示S1,S2;
(2)请写出上述过程所揭示的乘法公式;
(3)试利用这个公式计算:(2+1)(22+1)(24+1)(28+1)+1.
参考答案
一.完全平方公式
1.解:∵a+b=5,
∴a2+2ab+b2=25,
将ab=3,代入得:a2+b2+6=25,
∴a2+b2=19.
2.解:因为x﹣y=3,xy=1,
则x2+y2=(x﹣y)2+2xy=9+2=11,
故答案为:11
3.解:把知a+b=5两边平方,
可得:a2+2ab+b2=25,
把ab=3代入得:a2+b2=25﹣6=19,
故答案为:19.
4.解:展开式共有n+1项,系数和为2n.
故答案为:n+1,2n.
5.解:∵(2028﹣a)2+(2027﹣a)2=1,
∴(2028﹣a)2﹣2(2028﹣a)(2027﹣a)+(2027﹣a)2=1﹣2(2028﹣a)(2027﹣a),
即(2028﹣a﹣2027+a)2=1﹣2(2028﹣a)(2027﹣a),
整理得﹣2(2028﹣a)(2027﹣a)=0,
∴(2028﹣a)(2027﹣a)=0.
6.解:∵(a﹣b)2=(a+b)2﹣4ab,
∴(a﹣b)2=25﹣4×3=13.
∴a﹣b=±.
故答案为:±.
7.解:(a+b)2=a2+2ab+b2=16①,(a﹣b)2=a2﹣2ab+b2=14②,
①+②得:2(a2+b2)=30,
则a2+b2=15.
故答案为:15
8.解:根据题意得:(x+1)2﹣(1﹣x)(x﹣1)=6,
去括号得:x2+2x+1+x2﹣2x+1=6,
整理得:2x2=4,
解得:x=±.
故答案为:±
9.解:把x2﹣4x+1=0方程两边都除以x得,x+=4,
两边平方得,x2++2=16,
所以,x2+=14,
===.
故答案为:.
10.解:(1)因为m+n=6,mn=﹣3,
所以(m﹣2)(n﹣2)=mn﹣2m﹣2n+4=mn﹣2(m+n)+4=﹣3﹣2×6+4=﹣11.
(2)m2+n2=(m+n)2﹣2mn=62﹣2×(﹣3)=36+6=42.
11.解:∵a+b=3,
∴a2+2ab+b2=9,
∵ab=2,
∴a2+b2=9﹣2×2=5;
∴(a﹣b)2=a2﹣2ab+b2=5﹣2×2=1.
12.解:(1)∵x2+y2=(x+y)2﹣2xy,
∴当x+y=6,xy=4,x2+y2=(x+y)2﹣2xy=62﹣2×4=28;
(2)∵(x﹣y)2=(x+y)2﹣4xy,
∴当x+y=6,xy=4,(x﹣y)2=(x+y)2﹣4xy=62﹣4×4=20.
13.解:(1)∵(x+y)2+(x﹣y)2=x2+2xy+y2+x2﹣2xy+y2=2(x2+y2),
则x2+y2=[(x+y)2+(x﹣y)2]=×(6+2)=4;
(2)∵(x+y)2﹣(x﹣y)2=x2+2xy+y2﹣x2+2xy﹣y2=4xy,
∴xy=[(x+y)2﹣(x﹣y)2]=×(6﹣2)=1.
14.解:a2﹣ab+b2
=a2+b2﹣ab
=(a+b)2﹣2ab﹣ab
=(a+b)2﹣3ab
当a+b=3,ab=﹣4时,
原式=32﹣3×(﹣4)
=9+12
=21.
15.解:∵,
∴,
∴x2+=14,
∵(x﹣)2=x2+﹣2=12,
∴x﹣=.
16.解:(a+b)4=a4+4a3b+6a2b2+4ab3+b4.
故答案为:4,6,4.
17.解:(1)根据题意可推出第五行的数字为:1、5、10、10、5、1,
(2)(a+b)5=(a+b)3(a+b)2
=a5+5a4b+10a3b2+10a2b3+5ab4+b5,
(3)(a﹣b)5=(a﹣b)3(a﹣b)2
=(a3﹣3a2b+3ab2﹣b3)(a2﹣2ab+b2)
=a5﹣5a4b+10a3b2﹣10a2b3+5ab4﹣b5.
故答案为1、5、10、10、5、1.
二.完全平方公式的几何背景(共6小题)
18.解:S阴影=a2﹣(a﹣b)b=a2﹣ab+b2=(a2﹣ab+b2)=[(a+b)2﹣3ab],
又∵a+b=10,ab=18,
∴S阴影=[(a+b)2﹣3ab]=[(10)2﹣3×18]=23,
故答案为23.
19.解:S阴影=4S长方形=4ab①,
S阴影=S大正方形﹣S空白小正方形=(a+b)2﹣(b﹣a)2②,
由①②得:(a+b)2﹣(a﹣b)2=4ab.
故答案为:(a+b)2﹣(a﹣b)2=4ab.
20.解:一个边长为a的正方形的面积是a2,
4个边长为b的正方形的面积是4b2,
4个边长为a×b的长方形的面积是4ab,
∵a2+4ab+4b2=(a+2b)2,
∴拼成的正方形的边长最长可以为(a+2b),
故答案为:a+2b.
21.解:(1)两个阴影图形的面积和可表示为:
a2+b2或 (a+b)2﹣2ab;
由此得到怎样的等量关系:a2+b2=(a+b)2﹣2ab;
(2)∵a,b(a>b)满足a2+b2=53,ab=14,
∴①(a+b)2=a2+b2+2ab
=53+2×14=81
∴a+b=±9,
又∵a>0,b>0,∴a+b=9.
②(a﹣b)2=a2+b2﹣2ab
=53﹣2×14
=25,
∴a﹣b=±5
又∵a>b>0,
∴a﹣b=5.
22.解:(1)由题意,可得:(a+a+b)(b+a+b)=ab+a2+b2+a2+ab+ab+b2+ab+ab,
整理,得:(2a+b)(a+2b)=2a2+5ab+2b2.
(2)由(a+b)(a+3b)=a2+4ab+3b2可知,图形的两个边长为a+b和a+3b;里边的小图形有八个,一个面积为a2,4个面积为ab,3个面积为b2.
23.解:(1)图2的空白部分的边长是2a﹣b
(2)由图21﹣2可知,小正方形的面积=大正方形的面积﹣4个小长方形的面积,
∵大正方形的边长=2a+b=7,∴大正方形的面积=(2a+b)2=49,
又∵4个小长方形的面积之和=大长方形的面积=4a×2b=8ab=8×3=24,
∴小正方形的面积=(2a﹣b)2=49﹣24=25
(3)由图2可以看出,大正方形面积=空白部分的正方形的面积+四个小长方形的面积
即:(2a+b)2﹣(2a﹣b)2=8ab.
三.完全平方式
24.解:由题意,得a2+4ab+4b2
故选:A.
25.解:中间一项为加上或减去3x和2y积的2倍.
故k=±12.
26.解:∵x2﹣2(m+3)x+9是一个完全平方式,
∴m+3=±3,
解得:m=﹣6或m=0,
故答案为:﹣6或0
27.解:∵x2+(m﹣3)x+16是完全平方式,
∴m﹣3=±8,
解得:m=11或m=﹣5,
故答案为:11或﹣5
28.解:x2+mx+9=x2+mx+32,
∵x2+mx+9是完全平方式,
∴mx=±2 x 3,
解得:m=±6,
故答案为:±6.
四.平方差公式
29.解:①(x﹣1)(x+1)=x2﹣1;
②(x﹣1)(x2+x+1)=x3﹣1;
③(x﹣1)(x3+x2+x+1)=x4﹣1;
④(x﹣1)(x4+x3+x2+x+1)=x5﹣1;
⑤(x﹣1)(x5+x4+x3+x2+x+1)=x6﹣1;
…
由以上规律
(1)(x﹣1)(xn+xn﹣1+…+x+1)=xn+1﹣1;
(2)原式=(2﹣1)×(22022+22021+22020+…+22+2+1)=22023﹣1,
则22022+22021+22020+…+22+2+1=22023﹣1.
故答案为:①x2﹣1;②x3﹣1;(1)xn+1﹣1
五.平方差公式的几何背景
30.解:(1)利用正方形的面积公式可知:阴影部分的面积=a2﹣b2;
故答案为:a2﹣b2;
(2)由图可知矩形的宽是a﹣b,长是a+b,所以面积是(a+b)(a﹣b);
故答案为:a﹣b,a+b,(a+b)(a﹣b);
(3)(a+b)(a﹣b)=a2﹣b2(等式两边交换位置也可);
故答案为:(a+b)(a﹣b)=a2﹣b2;
(4)①解:原式=(10+0.3)×(10﹣0.3)
=102﹣0.32
=100﹣0.09
=99.91;
②解:原式=[2m+(n﹣p)] [2m﹣(n﹣p)]
=(2m)2﹣(n﹣p)2
=4m2﹣n2+2np﹣p2.
31.解:(1),S2=(a+b)(a﹣b);
(2)(a+b)(a﹣b)=a2﹣b2;
(3)原式=(2﹣1)(2+1)(22+1)(24+1)(28+1)+1
=(22﹣1)(22+1)(24+1)(28+1)+1
=(24﹣1)(24+1)(28+1)+1
=(28﹣1)(28+1)+1
=(216﹣1)+1
=216.
一.完全平方公式
1.已知a+b=5,ab=3,则a2+b2的值是 .
2.若x﹣y=3,xy=1,则x2+y2= .
3.已知a+b=5,ab=3,则a2+b2= .
4.我国宋朝数学家杨辉在他的著作《详解九章算法》中提出“杨辉三角”(如图),此图揭示了(a+b)n(n为非负整数)展开式的项数及各项系数的有关规律.
例如:(a+b)0=1,它只有一项,系数为1;系数和为1;
(a+b)1=a+b,它有两项,系数分别为1,1,系数和为2;
(a+b)2=a2+2ab+b2,它有三项,系数分别为1,2,1,系数和为4;
(a+b)3=a3+3a2b+3ab2+b3,它有四项,系数分别为1,3,3,1,系数和为8;…,
则(a+b)n的展开式共有 项,系数和为 .
5.已知(2028﹣a)2+(2027﹣a)2=1,则(2028﹣a) (2027﹣a)= .
6.已知a+b=5,ab=3,则a﹣b= .
7.若(a+b)2=16,(a﹣b)2=14,则代数式a2+b2的值为 .
8.定义=ad﹣bc,上述记号就叫做2阶行列式.若=6,x= .
9.如果x2﹣4x+1=0,那么= .
10.已知实数m,n满足m+n=6,mn=﹣3.
(1)求(m﹣2)(n﹣2)的值;
(2)求m2+n2的值.
11.已知a+b=3,ab=2,求a2+b2,(a﹣b)2的值.
12.已知:x+y=6,xy=4,求下列各式的值
(1)x2+y2
(2)(x﹣y)2.
13.已知:(x+y)2=6,(x﹣y)2=2,试求:
(1)x2+y2的值;
(2)xy的值.
14.已知a+b=3,ab=﹣4,求a2﹣ab+b2的值.
15.已知x+=4,求x﹣的值.
16.下表为杨辉三角系数表的一部分,它的作用是指导读者按规律写出形如:
(a+b)n(n为正整数)展开式的系数,请你仔细观察下表中的规律,填出(a+b)4展开式中所缺的系数.
(a+b)=a+b
(a+b)2=a2+2ab+b2
(a+b)3=a3+3a2b+3ab2+b3
(a+b)4=a4+ a3b+ a2b2+ ab3+b4.
17.我国宋代数学家杨辉写了一本书《详解九章算术》.书中记载了一个用数字排成的三角形我们叫作杨辉三角形
(a+b)0=1…1
(a+b)1=a+b…1 1
(a+b)2=a2+2ab+b2…1 2 1
(a+b)3=a3+3a2b+3ab2+b3…1 3 3 1
(a+b)4=a4+4a3b+6a2b2+4ab3+b4… 1 4 6 4 1
(1)请写出第五行的数字 ;
(2)第n行杨辉三角形数字与(a+b)n的展开结果关系如上图所示,请写出(a+b)5的展开结果;
(3)已知(a﹣b)1=a﹣b,(a﹣b)2=a2﹣2ab+b2,(a﹣b)3=a3﹣3a2b+3ab2﹣b3(a﹣b)4=a4﹣4a3b+6a2b2﹣4ab3+b4.请写出(a﹣b)5的展开结果.
二.完全平方公式的几何背景
18.如图,两个正方形边长分别为a,b,如果a+b=10,ab=18,则阴影部分的面积为 .
19.用4块完全相同的长方形拼成正方形(如图),用不同的方法,计算图中阴影部分的面积,可得到1个关于a,b的等式为 .
20.利用一个a×a的正方形,4个b×b的正方形,4个a×b的长方形,可拼成一个无缝隙且不重叠的大正方形,则这个大正方形的边长是 .
21.请认真观察图形,解答下列问题:
(1)根据图中条件,用两种方法表示两个阴影图形的面积的和(只需表示,不必化简);并由此得到怎样的等量关系?请用等式表示;
(2)如果图中的a,b(a>b)满足a2+b2=53,ab=14,
求:①a+b的值; ②a﹣b的值.
22.附加题:课本中多项式与多项式相乘是利用平面几何图形的面积来表示的,例如:(2a+b)(a+b)=2a2+3ab+b2就可以用图1或图2的面积来表示.
(1)请写出图3图形的面积表示的代数恒等式;
(2)试画出一个几何图形,使它的面积能表示(a+b)(a+3b)=a2+4ab+3b2.
23.如图1,将一个长为4a,宽为2b的长方形,沿图中虚线均匀分成4个小长方形,然后按图2形状拼成一个正方形.
(1)图2的空白部分的边长是多少?(用含a、b的式子表示)
(2)若2a+b=7,且ab=3,求图2中的空白正方形的面积.
(3)观察图2,用等式表示出(2a﹣b)2,ab和(2a+b)2的数量关系.
三.完全平方式
24.如图所示,有三种卡片,其中边长为a的正方形1张,边长为a、b的矩形卡片4张,边长为b的正方形4张用这9张卡片刚好能拼成一个正方形,则这个正方形的面积为( )
A.a2+4ab+4b2 B.4a2+8ab+4b2
C.4a2+4ab+b2 D.a2+2ab+b2
25.若9x2﹣kxy+4y2是一个完全平方式,则k的值是 .
26.已知x2﹣2(m+3)x+9是一个完全平方式,则m= .
27.若x2+(m﹣3)x+16是完全平方式,则m= .
28.已知x2+mx+9是完全平方式,则常数m等于 .
四.平方差公式
29.计算并观察、探究下列式子
①(x﹣1)(x+1)=
②(x﹣1)(x2+x+1)=
③(x﹣1)(x3+x2+x+1)=x4﹣1
④(x﹣1)(x4+x3+x2+x+1)=x5﹣1
⑤(x﹣1)(x5+x4+x3+x2+x+1)=x6﹣1
…
由以上规律
(1)填空:(x﹣1)(xn+xn﹣1+…+x+1)= .
(2)求:22022+22021+22020+…+22+2+1 的值.
五.平方差公式的几何背景
30.乘法公式的探究及应用.
(1)如图1,可以求出阴影部分的面积是 (写成两数平方差的形式);
(2)如图2,若将阴影部分裁剪下来,重新拼成一个长方形,它的宽是 ,长是 ,面积是 .(写成多项式乘法的形式)
(3)比较左、右两图的阴影部分面积,可以得到乘法公式 .(用式子表达)
(4)运用你所得到的公式,计算下列各题:
①10.3×9.7
②(2m+n﹣p)(2m﹣n+p)
31.如图1所示,边长为a的正方形中有一个边长为b的小正方形,如图2所示是由图1中阴影部分拼成的一个长方形.
(1)设图1中阴影部分面积为S1,图2中阴影部分面积为S2.请直接用含a,b的代数式表示S1,S2;
(2)请写出上述过程所揭示的乘法公式;
(3)试利用这个公式计算:(2+1)(22+1)(24+1)(28+1)+1.
参考答案
一.完全平方公式
1.解:∵a+b=5,
∴a2+2ab+b2=25,
将ab=3,代入得:a2+b2+6=25,
∴a2+b2=19.
2.解:因为x﹣y=3,xy=1,
则x2+y2=(x﹣y)2+2xy=9+2=11,
故答案为:11
3.解:把知a+b=5两边平方,
可得:a2+2ab+b2=25,
把ab=3代入得:a2+b2=25﹣6=19,
故答案为:19.
4.解:展开式共有n+1项,系数和为2n.
故答案为:n+1,2n.
5.解:∵(2028﹣a)2+(2027﹣a)2=1,
∴(2028﹣a)2﹣2(2028﹣a)(2027﹣a)+(2027﹣a)2=1﹣2(2028﹣a)(2027﹣a),
即(2028﹣a﹣2027+a)2=1﹣2(2028﹣a)(2027﹣a),
整理得﹣2(2028﹣a)(2027﹣a)=0,
∴(2028﹣a)(2027﹣a)=0.
6.解:∵(a﹣b)2=(a+b)2﹣4ab,
∴(a﹣b)2=25﹣4×3=13.
∴a﹣b=±.
故答案为:±.
7.解:(a+b)2=a2+2ab+b2=16①,(a﹣b)2=a2﹣2ab+b2=14②,
①+②得:2(a2+b2)=30,
则a2+b2=15.
故答案为:15
8.解:根据题意得:(x+1)2﹣(1﹣x)(x﹣1)=6,
去括号得:x2+2x+1+x2﹣2x+1=6,
整理得:2x2=4,
解得:x=±.
故答案为:±
9.解:把x2﹣4x+1=0方程两边都除以x得,x+=4,
两边平方得,x2++2=16,
所以,x2+=14,
===.
故答案为:.
10.解:(1)因为m+n=6,mn=﹣3,
所以(m﹣2)(n﹣2)=mn﹣2m﹣2n+4=mn﹣2(m+n)+4=﹣3﹣2×6+4=﹣11.
(2)m2+n2=(m+n)2﹣2mn=62﹣2×(﹣3)=36+6=42.
11.解:∵a+b=3,
∴a2+2ab+b2=9,
∵ab=2,
∴a2+b2=9﹣2×2=5;
∴(a﹣b)2=a2﹣2ab+b2=5﹣2×2=1.
12.解:(1)∵x2+y2=(x+y)2﹣2xy,
∴当x+y=6,xy=4,x2+y2=(x+y)2﹣2xy=62﹣2×4=28;
(2)∵(x﹣y)2=(x+y)2﹣4xy,
∴当x+y=6,xy=4,(x﹣y)2=(x+y)2﹣4xy=62﹣4×4=20.
13.解:(1)∵(x+y)2+(x﹣y)2=x2+2xy+y2+x2﹣2xy+y2=2(x2+y2),
则x2+y2=[(x+y)2+(x﹣y)2]=×(6+2)=4;
(2)∵(x+y)2﹣(x﹣y)2=x2+2xy+y2﹣x2+2xy﹣y2=4xy,
∴xy=[(x+y)2﹣(x﹣y)2]=×(6﹣2)=1.
14.解:a2﹣ab+b2
=a2+b2﹣ab
=(a+b)2﹣2ab﹣ab
=(a+b)2﹣3ab
当a+b=3,ab=﹣4时,
原式=32﹣3×(﹣4)
=9+12
=21.
15.解:∵,
∴,
∴x2+=14,
∵(x﹣)2=x2+﹣2=12,
∴x﹣=.
16.解:(a+b)4=a4+4a3b+6a2b2+4ab3+b4.
故答案为:4,6,4.
17.解:(1)根据题意可推出第五行的数字为:1、5、10、10、5、1,
(2)(a+b)5=(a+b)3(a+b)2
=a5+5a4b+10a3b2+10a2b3+5ab4+b5,
(3)(a﹣b)5=(a﹣b)3(a﹣b)2
=(a3﹣3a2b+3ab2﹣b3)(a2﹣2ab+b2)
=a5﹣5a4b+10a3b2﹣10a2b3+5ab4﹣b5.
故答案为1、5、10、10、5、1.
二.完全平方公式的几何背景(共6小题)
18.解:S阴影=a2﹣(a﹣b)b=a2﹣ab+b2=(a2﹣ab+b2)=[(a+b)2﹣3ab],
又∵a+b=10,ab=18,
∴S阴影=[(a+b)2﹣3ab]=[(10)2﹣3×18]=23,
故答案为23.
19.解:S阴影=4S长方形=4ab①,
S阴影=S大正方形﹣S空白小正方形=(a+b)2﹣(b﹣a)2②,
由①②得:(a+b)2﹣(a﹣b)2=4ab.
故答案为:(a+b)2﹣(a﹣b)2=4ab.
20.解:一个边长为a的正方形的面积是a2,
4个边长为b的正方形的面积是4b2,
4个边长为a×b的长方形的面积是4ab,
∵a2+4ab+4b2=(a+2b)2,
∴拼成的正方形的边长最长可以为(a+2b),
故答案为:a+2b.
21.解:(1)两个阴影图形的面积和可表示为:
a2+b2或 (a+b)2﹣2ab;
由此得到怎样的等量关系:a2+b2=(a+b)2﹣2ab;
(2)∵a,b(a>b)满足a2+b2=53,ab=14,
∴①(a+b)2=a2+b2+2ab
=53+2×14=81
∴a+b=±9,
又∵a>0,b>0,∴a+b=9.
②(a﹣b)2=a2+b2﹣2ab
=53﹣2×14
=25,
∴a﹣b=±5
又∵a>b>0,
∴a﹣b=5.
22.解:(1)由题意,可得:(a+a+b)(b+a+b)=ab+a2+b2+a2+ab+ab+b2+ab+ab,
整理,得:(2a+b)(a+2b)=2a2+5ab+2b2.
(2)由(a+b)(a+3b)=a2+4ab+3b2可知,图形的两个边长为a+b和a+3b;里边的小图形有八个,一个面积为a2,4个面积为ab,3个面积为b2.
23.解:(1)图2的空白部分的边长是2a﹣b
(2)由图21﹣2可知,小正方形的面积=大正方形的面积﹣4个小长方形的面积,
∵大正方形的边长=2a+b=7,∴大正方形的面积=(2a+b)2=49,
又∵4个小长方形的面积之和=大长方形的面积=4a×2b=8ab=8×3=24,
∴小正方形的面积=(2a﹣b)2=49﹣24=25
(3)由图2可以看出,大正方形面积=空白部分的正方形的面积+四个小长方形的面积
即:(2a+b)2﹣(2a﹣b)2=8ab.
三.完全平方式
24.解:由题意,得a2+4ab+4b2
故选:A.
25.解:中间一项为加上或减去3x和2y积的2倍.
故k=±12.
26.解:∵x2﹣2(m+3)x+9是一个完全平方式,
∴m+3=±3,
解得:m=﹣6或m=0,
故答案为:﹣6或0
27.解:∵x2+(m﹣3)x+16是完全平方式,
∴m﹣3=±8,
解得:m=11或m=﹣5,
故答案为:11或﹣5
28.解:x2+mx+9=x2+mx+32,
∵x2+mx+9是完全平方式,
∴mx=±2 x 3,
解得:m=±6,
故答案为:±6.
四.平方差公式
29.解:①(x﹣1)(x+1)=x2﹣1;
②(x﹣1)(x2+x+1)=x3﹣1;
③(x﹣1)(x3+x2+x+1)=x4﹣1;
④(x﹣1)(x4+x3+x2+x+1)=x5﹣1;
⑤(x﹣1)(x5+x4+x3+x2+x+1)=x6﹣1;
…
由以上规律
(1)(x﹣1)(xn+xn﹣1+…+x+1)=xn+1﹣1;
(2)原式=(2﹣1)×(22022+22021+22020+…+22+2+1)=22023﹣1,
则22022+22021+22020+…+22+2+1=22023﹣1.
故答案为:①x2﹣1;②x3﹣1;(1)xn+1﹣1
五.平方差公式的几何背景
30.解:(1)利用正方形的面积公式可知:阴影部分的面积=a2﹣b2;
故答案为:a2﹣b2;
(2)由图可知矩形的宽是a﹣b,长是a+b,所以面积是(a+b)(a﹣b);
故答案为:a﹣b,a+b,(a+b)(a﹣b);
(3)(a+b)(a﹣b)=a2﹣b2(等式两边交换位置也可);
故答案为:(a+b)(a﹣b)=a2﹣b2;
(4)①解:原式=(10+0.3)×(10﹣0.3)
=102﹣0.32
=100﹣0.09
=99.91;
②解:原式=[2m+(n﹣p)] [2m﹣(n﹣p)]
=(2m)2﹣(n﹣p)2
=4m2﹣n2+2np﹣p2.
31.解:(1),S2=(a+b)(a﹣b);
(2)(a+b)(a﹣b)=a2﹣b2;
(3)原式=(2﹣1)(2+1)(22+1)(24+1)(28+1)+1
=(22﹣1)(22+1)(24+1)(28+1)+1
=(24﹣1)(24+1)(28+1)+1
=(28﹣1)(28+1)+1
=(216﹣1)+1
=216.
