人教版九年级数学下册 26-2 实际问题与反比例函数2 (共17张ppt)
文档属性
| 名称 | 人教版九年级数学下册 26-2 实际问题与反比例函数2 (共17张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-26 21:09:51 | ||
图片预览






文档简介
(共17张PPT)
第二十六章 反比例函数
26.2 实际问题与反比例函数
第二课时
学习目标
1.经历利用反比例函数知识解决物理问题的过程,认识到数学知识
可以解决跨学科问题。(重点)
2.通过分析实际问题中变量之间的关系,建立反比例函数模型,
进而解决问题,从而体会建模思想的应用。(难点)
新课导入
复习引入
1.当功W一定时,力F与物体在力的方向上通过的位移s成反比例关系,
可以写成________(W是常数)
2.当压力F一定时,压强P与受力面积S之间成反比例关系,
可以写成__________(F是常数)
3.在某一电路中,保持电压U不变,电流I与电阻R成反比例关系,
可以写成_______(U是常数)
4.当物体的质量m一定时,物体的密度ρ关于体积V的函数
解析式是________(m是常数)
新知探究
(一)反比例函数在物理中的应用
例1:小伟欲用撬棍撬动一块大石头,已知阻力和阻力臂
分别为1200N和0.5m
(1)动力F与动力臂 有怎样的函数关系?
(2)当动力臂为1.5m时,撬动石头至少需要多大的力?
若想使动力F不超过题(2)中所用力的一半,
则动力臂至少要加多长?
新知探究
(一)反比例函数在物理中的应用
解: (1)根据“杠杆原理”,得:
∴F关于 的函数关系式为
(2)当 时,
∴当动力臂为1.5m时,撬动石头至少需要400N的力。
新知探究
(一)反比例函数在物理中的应用
(3)当 时,代入 中,
得:
∴
∴若想用力不超过200N,则动力臂至少要加长1.5m
新知探究
(一)反比例函数在物理中的应用
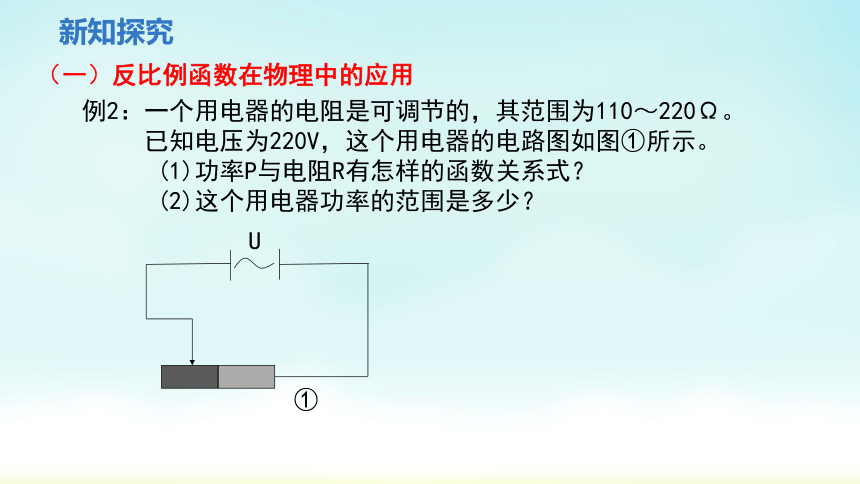
例2:一个用电器的电阻是可调节的,其范围为110~220Ω。
已知电压为220V,这个用电器的电路图如图①所示。
(1)功率P与电阻R有怎样的函数关系式?
(2)这个用电器功率的范围是多少?
U
①
新知探究
(一)反比例函数在物理中的应用
解:(1)根据电学知识,当U=220时,得:
(2)根据反比例函数的性质可知,电阻越大,功率越小。
当电阻最小R=110时,代入 得:
当电阻最大R=220时,代入 得:
∴用电器的功率范围为220~440W
新知探究
(二)与反比例函数有关的分段函数问题
例3:某药品研究所开发一种抗菌新药,经多年动物实验,
首次用于临床人体实验,测得承认服药后血液中药物浓度
y(微克/毫升)与服药时间x(小时)之间函数关系如图②
所示(当4≤x≤10)时,y与x成反比例)
(1)根据图像分别求出血液中药物浓度上升和
下降阶段y与x之间的函数关系式。
(2)问血液中药物浓度不低于4微克/毫升的持续时间为多少小时?
y(微克/毫升)
8
O
4
x
10
新知探究
(二)与反比例函数有关的分段函数问题
y(微克/毫升)
8
O
4
x
10
解:(1)根据图像可知:
血液中药物浓度上升时为正比例函数,
下降时为反比例函数,
∴设当0≤x≤4时,y=kx, 当4≤x≤10时,
将(4,8)代入y=kx中得:8=4k
k=2
∴当0≤x≤4时,y=2x
将(4,8)代入 中,得:m=32
∴当4≤x≤10时,
新知探究
(二)与反比例函数有关的分段函数问题
y(微克/毫升)
8
O
4
x
10
(2)当y=4时,代入y=2x中得:x=2
当y=4时代入 中得: x=8
8-2=6
∴血液中浓度不低于4微克/毫升的持续
时间为6小时。
课堂小结
归纳总结:
1.在利用反比例函数解决与其他学科有关的实际问题时,
一定要注意 中,k为常数,且k≠0这一条件,
要结合学科知识,深入探究问题。
2.分段函数要注重取值范围,根据图像求出解析式,
从而解决实际问题。
课堂训练
1.已知电流I(单位:A)、电压U(单位:V)、电阻R(单位:Ω)
之间的关系为,当电压为定值时,I关于R的函数图像是( )
C
A
B
C
D
I
I
I
I
O
O
R
O
R
O
R
R
课堂训练
2.已知力F所做的功是15焦,则力F与物体在力的方向上
通过的距离s的图像大致是下图中的的( )
F
F
F
F
O
O
O
O
s
s
s
s
A
D
C
B
B
课堂训练
3.小明欲用撬棍撬动一块大石头,已知阻力和阻力臂不变,
分别为1200牛顿和0.5米,则动力F与动力臂L的
函数关系式是__________
课堂训练
4 .有一个可以改变体积的密闭容器内装有一定质量的二氧化碳,
当改变容积的体积时,气体的密度也会随之改变,密度ρ(单位:kg/m3)
是体积V(单位:m3)的反比例函数,它的图像如图③所示,当V=2m3时,
气体的密度是____________kg/m3
ρ(kg/m3)
V(m3)
2
O
4
③
4
课堂训练
5.如图④,制作某金属工具时,先将材料煅烧6min,使温度升到800℃,
在停止煅烧进行锻造,8min时温度降为600℃,煅烧时温度T与时间x
成一次函数关系;锻造时温度T与时间x成反比例函数关系,
该材料初始温度是32℃
(1)分别求出材料煅烧和锻造时T与x的函数解析式。
(2)根据工艺要求,当材料温度低于480℃时,须停止操作,
那么锻造的操作时间有多长?
T(℃)
800
600
32
x(min)
O
6
8
④
第二十六章 反比例函数
26.2 实际问题与反比例函数
第二课时
学习目标
1.经历利用反比例函数知识解决物理问题的过程,认识到数学知识
可以解决跨学科问题。(重点)
2.通过分析实际问题中变量之间的关系,建立反比例函数模型,
进而解决问题,从而体会建模思想的应用。(难点)
新课导入
复习引入
1.当功W一定时,力F与物体在力的方向上通过的位移s成反比例关系,
可以写成________(W是常数)
2.当压力F一定时,压强P与受力面积S之间成反比例关系,
可以写成__________(F是常数)
3.在某一电路中,保持电压U不变,电流I与电阻R成反比例关系,
可以写成_______(U是常数)
4.当物体的质量m一定时,物体的密度ρ关于体积V的函数
解析式是________(m是常数)
新知探究
(一)反比例函数在物理中的应用
例1:小伟欲用撬棍撬动一块大石头,已知阻力和阻力臂
分别为1200N和0.5m
(1)动力F与动力臂 有怎样的函数关系?
(2)当动力臂为1.5m时,撬动石头至少需要多大的力?
若想使动力F不超过题(2)中所用力的一半,
则动力臂至少要加多长?
新知探究
(一)反比例函数在物理中的应用
解: (1)根据“杠杆原理”,得:
∴F关于 的函数关系式为
(2)当 时,
∴当动力臂为1.5m时,撬动石头至少需要400N的力。
新知探究
(一)反比例函数在物理中的应用
(3)当 时,代入 中,
得:
∴
∴若想用力不超过200N,则动力臂至少要加长1.5m
新知探究
(一)反比例函数在物理中的应用
例2:一个用电器的电阻是可调节的,其范围为110~220Ω。
已知电压为220V,这个用电器的电路图如图①所示。
(1)功率P与电阻R有怎样的函数关系式?
(2)这个用电器功率的范围是多少?
U
①
新知探究
(一)反比例函数在物理中的应用
解:(1)根据电学知识,当U=220时,得:
(2)根据反比例函数的性质可知,电阻越大,功率越小。
当电阻最小R=110时,代入 得:
当电阻最大R=220时,代入 得:
∴用电器的功率范围为220~440W
新知探究
(二)与反比例函数有关的分段函数问题
例3:某药品研究所开发一种抗菌新药,经多年动物实验,
首次用于临床人体实验,测得承认服药后血液中药物浓度
y(微克/毫升)与服药时间x(小时)之间函数关系如图②
所示(当4≤x≤10)时,y与x成反比例)
(1)根据图像分别求出血液中药物浓度上升和
下降阶段y与x之间的函数关系式。
(2)问血液中药物浓度不低于4微克/毫升的持续时间为多少小时?
y(微克/毫升)
8
O
4
x
10
新知探究
(二)与反比例函数有关的分段函数问题
y(微克/毫升)
8
O
4
x
10
解:(1)根据图像可知:
血液中药物浓度上升时为正比例函数,
下降时为反比例函数,
∴设当0≤x≤4时,y=kx, 当4≤x≤10时,
将(4,8)代入y=kx中得:8=4k
k=2
∴当0≤x≤4时,y=2x
将(4,8)代入 中,得:m=32
∴当4≤x≤10时,
新知探究
(二)与反比例函数有关的分段函数问题
y(微克/毫升)
8
O
4
x
10
(2)当y=4时,代入y=2x中得:x=2
当y=4时代入 中得: x=8
8-2=6
∴血液中浓度不低于4微克/毫升的持续
时间为6小时。
课堂小结
归纳总结:
1.在利用反比例函数解决与其他学科有关的实际问题时,
一定要注意 中,k为常数,且k≠0这一条件,
要结合学科知识,深入探究问题。
2.分段函数要注重取值范围,根据图像求出解析式,
从而解决实际问题。
课堂训练
1.已知电流I(单位:A)、电压U(单位:V)、电阻R(单位:Ω)
之间的关系为,当电压为定值时,I关于R的函数图像是( )
C
A
B
C
D
I
I
I
I
O
O
R
O
R
O
R
R
课堂训练
2.已知力F所做的功是15焦,则力F与物体在力的方向上
通过的距离s的图像大致是下图中的的( )
F
F
F
F
O
O
O
O
s
s
s
s
A
D
C
B
B
课堂训练
3.小明欲用撬棍撬动一块大石头,已知阻力和阻力臂不变,
分别为1200牛顿和0.5米,则动力F与动力臂L的
函数关系式是__________
课堂训练
4 .有一个可以改变体积的密闭容器内装有一定质量的二氧化碳,
当改变容积的体积时,气体的密度也会随之改变,密度ρ(单位:kg/m3)
是体积V(单位:m3)的反比例函数,它的图像如图③所示,当V=2m3时,
气体的密度是____________kg/m3
ρ(kg/m3)
V(m3)
2
O
4
③
4
课堂训练
5.如图④,制作某金属工具时,先将材料煅烧6min,使温度升到800℃,
在停止煅烧进行锻造,8min时温度降为600℃,煅烧时温度T与时间x
成一次函数关系;锻造时温度T与时间x成反比例函数关系,
该材料初始温度是32℃
(1)分别求出材料煅烧和锻造时T与x的函数解析式。
(2)根据工艺要求,当材料温度低于480℃时,须停止操作,
那么锻造的操作时间有多长?
T(℃)
800
600
32
x(min)
O
6
8
④
