人教版九年级数学下册 27-2-1 相似三角形的判定1 (共20张ppt)
文档属性
| 名称 | 人教版九年级数学下册 27-2-1 相似三角形的判定1 (共20张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-26 21:16:39 | ||
图片预览




文档简介
(共20张PPT)
第二十七章 相似
27.2.1相似三角形的判定
第一课时
学习目标
1.理解相似三角形的概念。
2.掌握平行线分线段成比例定理,并能用其进行简单的计算和证明。
3.掌握基本定理的推导过程,并能利用其判定三角形相似。
新课导入
1.两个多边形相似要满足什么条件?
2.类比相似多边形的概念说明三角形相似需满足的条件?
3.三角形全等的判定方法有哪些?
4.类比三角形全等的判定方法,三角形相似的判定有没有简单
的方法呢?
复习提问:
新知探究
4.性质:相似三角形的三个角分别_________,三条边_________.
(一)相似三角形的概念
1.概念:三个角分别______,三条边________的两个三角形相似.
2.记法:△ABC与△A1B1C1相似,记作:____________
3.相似比:相似三角形_________________.
相等
成比例
△ABC∽△A1B1C1
对应边的比
相等
成比例
新知探究
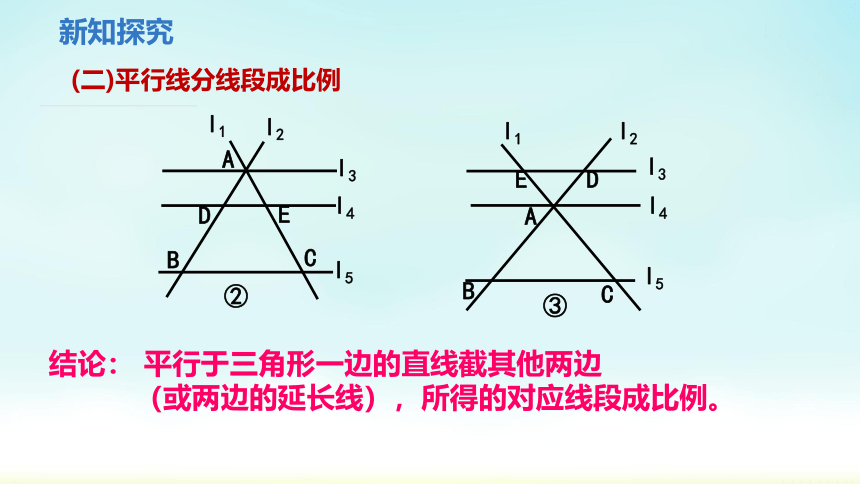
(二)平行线分线段成比例
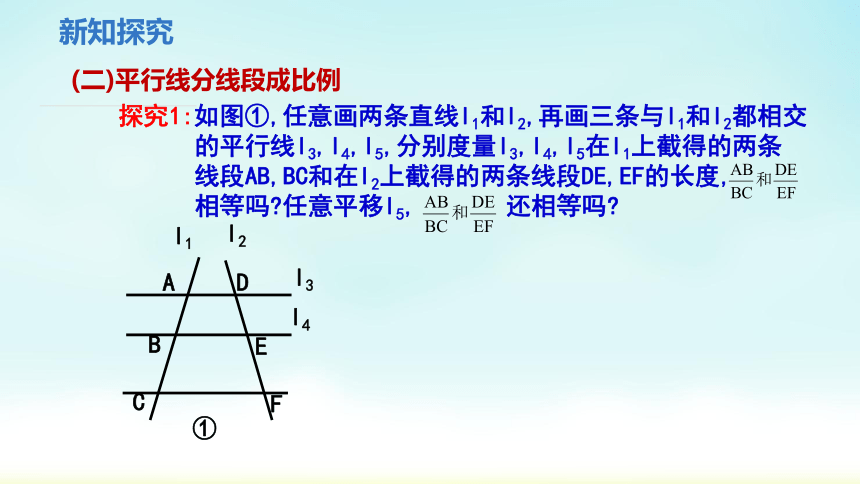
探究1:如图①,任意画两条直线l1和l2,再画三条与l1和l2都相交
的平行线l3,l4,l5,分别度量l3,l4,l5在l1上截得的两条
线段AB,BC和在l2上截得的两条线段DE,EF的长度,
相等吗 任意平移l5, 还相等吗
l1
l2
l3
l4
A
C
B
D
E
F
①
新知探究
(二)平行线分线段成比例
l1
l2
l3
l4
A
C
B
D
E
F
①
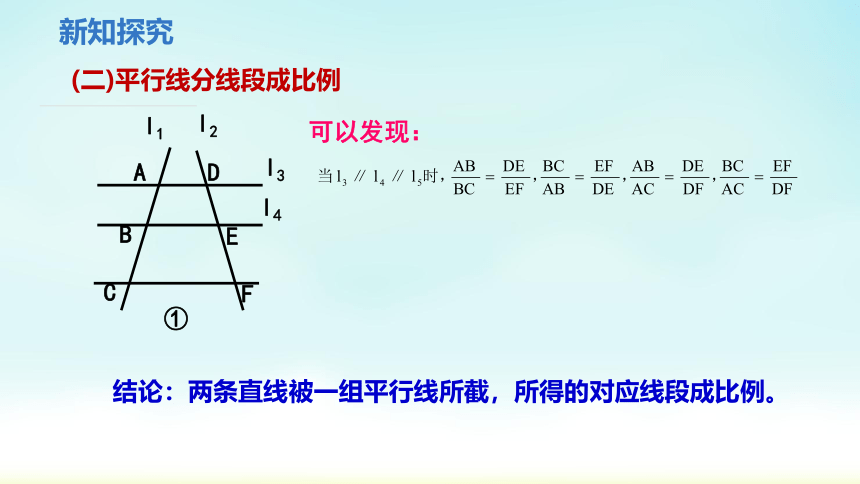
可以发现:
结论:两条直线被一组平行线所截,所得的对应线段成比例。
新知探究
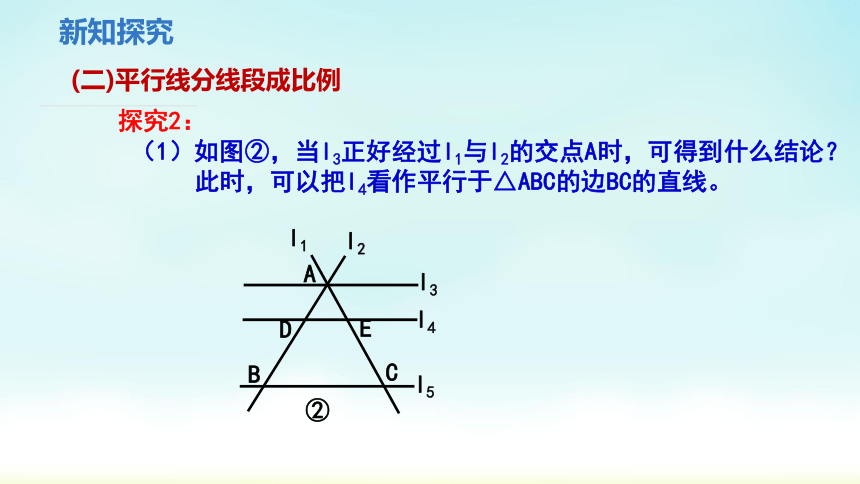
探究2:
(1)如图②,当l3正好经过l1与l2的交点A时,可得到什么结论?
此时,可以把l4看作平行于△ABC的边BC的直线。
(二)平行线分线段成比例
A
E
D
B
C
l1
l2
l3
l4
l5
②
新知探究
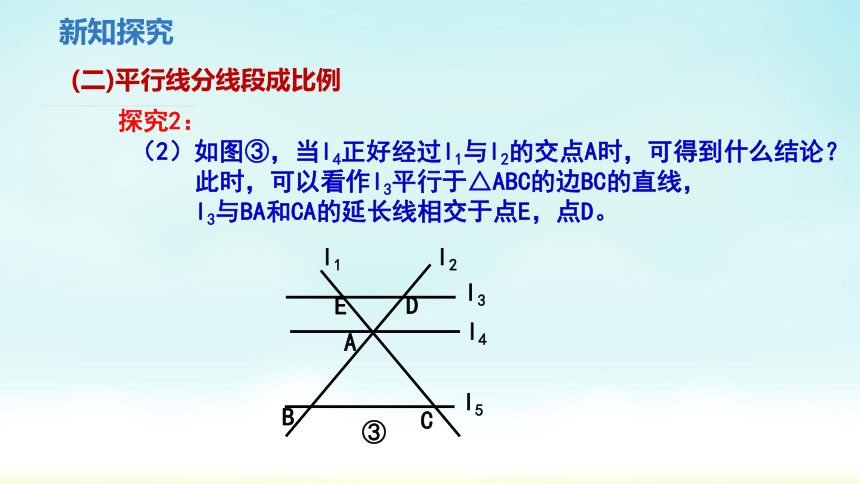
探究2:
(2)如图③,当l4正好经过l1与l2的交点A时,可得到什么结论?
此时,可以看作l3平行于△ABC的边BC的直线,
l3与BA和CA的延长线相交于点E,点D。
(二)平行线分线段成比例
C
A
l1
l2
l3
l4
③
E
D
B
l5
新知探究
(二)平行线分线段成比例
结论: 平行于三角形一边的直线截其他两边
(或两边的延长线),所得的对应线段成比例。
C
A
l1
l2
l3
l4
③
E
D
B
l5
A
E
D
B
C
l1
l2
l3
l4
l5
②
新知探究
(二)平行线分线段成比例
例1:如图④,若AE∥CF∥DG,AB∶BC∶CD=1∶2∶3,BG=30cm,
求BE和FG的长.
E
A
B
C
F
D
G
④
解:
新知探究
(三) 三角形相似的判定定理
探究3:
如图⑤,在△ABC中,DE∥BC,且DE分别交AB,AC于点D,E,
△ADE与△ABC是否相似
⑤
A
D
E
B
C
新知探究
(三) 三角形相似的判定定理
F
A
D
E
B
C
⑥
证明:
新知探究
结论:
平行于三角形一边的直线和其他两边相交,所构成的三角形
与原三角形相似.
(三) 三角形相似的判定定理
A
D
E
B
C
⑥
F
新知探究
(三) 三角形相似的判定定理
例2:如图⑦,DE∥BC,且DB=AE,若AB=5,AC=10,
(1)求AE的长.
(2)求 得值.
A
D
E
B
C
⑦
解:
新知探究
(三) 三角形相似的判定定理
例2:如图⑦,DE∥BC,且DB=AE,若AB=5,AC=10,
(1)求AE的长.
(2)求 得值.
A
D
E
B
C
⑦
解:
课堂小结
(一)相似三角形的概念
1.概念:三个角分别相等,三条边成比例的两个三角形相似.
2.记法:△ABC与△A1B1C1相似,记作:△ABC∽△A1B1C1
3.相似比:相似三角形对应边的比.
4.性质:相似三角形的三个角分别相等,三条边成比例.
(二)平行线分线段成比例
1.两条直线被一组平行线所截,所得的对应线段成比例。
2.平行于三角形一边的直线截其他两边(或两边的延长线),
所得的对应线段成比例。
(三) 三角形相似的判定定理
平行于三角形一边的直线和其他两边相交,所构成的三角形
与原三角形相似.
课堂训练
1.如图⑧,DE∥BC,则下面比例式不成立的是( )
B
⑧
A
D
E
B
C
A
B
D
C
E
F
⑨
2.如图⑨,已知AB∥CD∥EF,那么下列结论正确的是( )
A
课堂训练
3.如图⑩,已知AD与BC相交于点O,AB∥CD,则( )
A.△AOB∽△COD B.△AOB∽△DOC
C. △ABO∽△CDO D.△ABO∽△DOC
B
⑩
B
A
O
D
C
课堂训练
C
4.如图 ,在 ABCD中,点E在边AD上,射线CE,BA交于点F,
下列等式成立的是( )
F
C
B
D
E
A
课堂训练
5.如图 ,DE∥BC,DF∥AC,AD=4cm,BD=8cm,DE=5cm,求线段BF的长.
A
D
E
B
F
C
第二十七章 相似
27.2.1相似三角形的判定
第一课时
学习目标
1.理解相似三角形的概念。
2.掌握平行线分线段成比例定理,并能用其进行简单的计算和证明。
3.掌握基本定理的推导过程,并能利用其判定三角形相似。
新课导入
1.两个多边形相似要满足什么条件?
2.类比相似多边形的概念说明三角形相似需满足的条件?
3.三角形全等的判定方法有哪些?
4.类比三角形全等的判定方法,三角形相似的判定有没有简单
的方法呢?
复习提问:
新知探究
4.性质:相似三角形的三个角分别_________,三条边_________.
(一)相似三角形的概念
1.概念:三个角分别______,三条边________的两个三角形相似.
2.记法:△ABC与△A1B1C1相似,记作:____________
3.相似比:相似三角形_________________.
相等
成比例
△ABC∽△A1B1C1
对应边的比
相等
成比例
新知探究
(二)平行线分线段成比例
探究1:如图①,任意画两条直线l1和l2,再画三条与l1和l2都相交
的平行线l3,l4,l5,分别度量l3,l4,l5在l1上截得的两条
线段AB,BC和在l2上截得的两条线段DE,EF的长度,
相等吗 任意平移l5, 还相等吗
l1
l2
l3
l4
A
C
B
D
E
F
①
新知探究
(二)平行线分线段成比例
l1
l2
l3
l4
A
C
B
D
E
F
①
可以发现:
结论:两条直线被一组平行线所截,所得的对应线段成比例。
新知探究
探究2:
(1)如图②,当l3正好经过l1与l2的交点A时,可得到什么结论?
此时,可以把l4看作平行于△ABC的边BC的直线。
(二)平行线分线段成比例
A
E
D
B
C
l1
l2
l3
l4
l5
②
新知探究
探究2:
(2)如图③,当l4正好经过l1与l2的交点A时,可得到什么结论?
此时,可以看作l3平行于△ABC的边BC的直线,
l3与BA和CA的延长线相交于点E,点D。
(二)平行线分线段成比例
C
A
l1
l2
l3
l4
③
E
D
B
l5
新知探究
(二)平行线分线段成比例
结论: 平行于三角形一边的直线截其他两边
(或两边的延长线),所得的对应线段成比例。
C
A
l1
l2
l3
l4
③
E
D
B
l5
A
E
D
B
C
l1
l2
l3
l4
l5
②
新知探究
(二)平行线分线段成比例
例1:如图④,若AE∥CF∥DG,AB∶BC∶CD=1∶2∶3,BG=30cm,
求BE和FG的长.
E
A
B
C
F
D
G
④
解:
新知探究
(三) 三角形相似的判定定理
探究3:
如图⑤,在△ABC中,DE∥BC,且DE分别交AB,AC于点D,E,
△ADE与△ABC是否相似
⑤
A
D
E
B
C
新知探究
(三) 三角形相似的判定定理
F
A
D
E
B
C
⑥
证明:
新知探究
结论:
平行于三角形一边的直线和其他两边相交,所构成的三角形
与原三角形相似.
(三) 三角形相似的判定定理
A
D
E
B
C
⑥
F
新知探究
(三) 三角形相似的判定定理
例2:如图⑦,DE∥BC,且DB=AE,若AB=5,AC=10,
(1)求AE的长.
(2)求 得值.
A
D
E
B
C
⑦
解:
新知探究
(三) 三角形相似的判定定理
例2:如图⑦,DE∥BC,且DB=AE,若AB=5,AC=10,
(1)求AE的长.
(2)求 得值.
A
D
E
B
C
⑦
解:
课堂小结
(一)相似三角形的概念
1.概念:三个角分别相等,三条边成比例的两个三角形相似.
2.记法:△ABC与△A1B1C1相似,记作:△ABC∽△A1B1C1
3.相似比:相似三角形对应边的比.
4.性质:相似三角形的三个角分别相等,三条边成比例.
(二)平行线分线段成比例
1.两条直线被一组平行线所截,所得的对应线段成比例。
2.平行于三角形一边的直线截其他两边(或两边的延长线),
所得的对应线段成比例。
(三) 三角形相似的判定定理
平行于三角形一边的直线和其他两边相交,所构成的三角形
与原三角形相似.
课堂训练
1.如图⑧,DE∥BC,则下面比例式不成立的是( )
B
⑧
A
D
E
B
C
A
B
D
C
E
F
⑨
2.如图⑨,已知AB∥CD∥EF,那么下列结论正确的是( )
A
课堂训练
3.如图⑩,已知AD与BC相交于点O,AB∥CD,则( )
A.△AOB∽△COD B.△AOB∽△DOC
C. △ABO∽△CDO D.△ABO∽△DOC
B
⑩
B
A
O
D
C
课堂训练
C
4.如图 ,在 ABCD中,点E在边AD上,射线CE,BA交于点F,
下列等式成立的是( )
F
C
B
D
E
A
课堂训练
5.如图 ,DE∥BC,DF∥AC,AD=4cm,BD=8cm,DE=5cm,求线段BF的长.
A
D
E
B
F
C
