人教版九年级数学下册 27-3-2 平面直角坐标系的位似 课件(共14张PPT)
文档属性
| 名称 | 人教版九年级数学下册 27-3-2 平面直角坐标系的位似 课件(共14张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-26 21:19:56 | ||
图片预览





文档简介
(共14张PPT)
第二十七章 相似
27.3 位似
第2课时
学习目标
1.让学生理解掌握位似图形在平面直角坐标系上的应用,
即会根据相似比,求位似图形的顶点,以及根据位似图形
对应点的坐标,求位似图形的相似比和在平面直角坐标系
中作出位似图形.
2.了解四种变化(平移,轴对称,旋转和位似)的异同,并能在
复杂的图形中找出这些变换.
新课导入
复习提问:
1.A(x,y)关于x轴对称的点的坐标是什么
2.A(x,y)关于y轴对称的点的坐标是什么
3.A(x,y)关于原点对称的点的坐标是什么
新知探究
( 一 )探究新知,得出结论
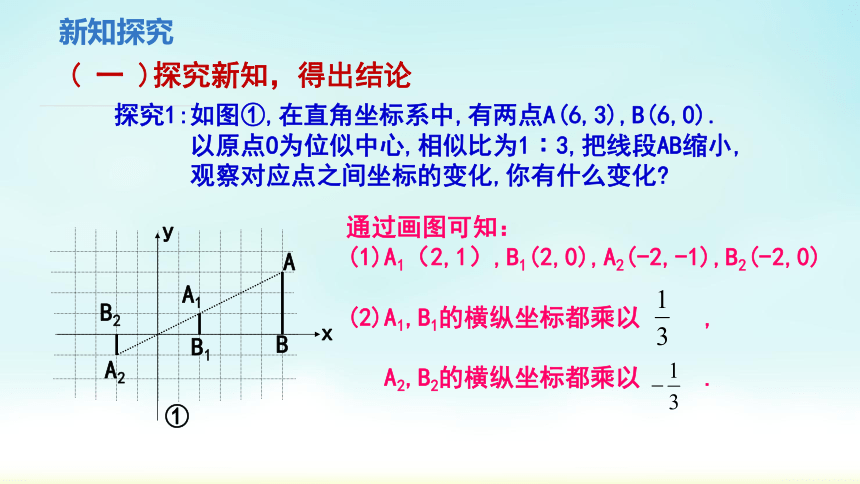
探究1:如图①,在直角坐标系中,有两点A(6,3),B(6,0).
以原点O为位似中心,相似比为1∶3,把线段AB缩小,
观察对应点之间坐标的变化,你有什么变化
①
A
B1
B2
A2
A1
B
y
x
通过画图可知:
(1)A1(2,1),B1(2,0),A2(-2,-1),B2(-2,0)
(2)A1,B1的横纵坐标都乘以 ,
A2,B2的横纵坐标都乘以 .
新知探究
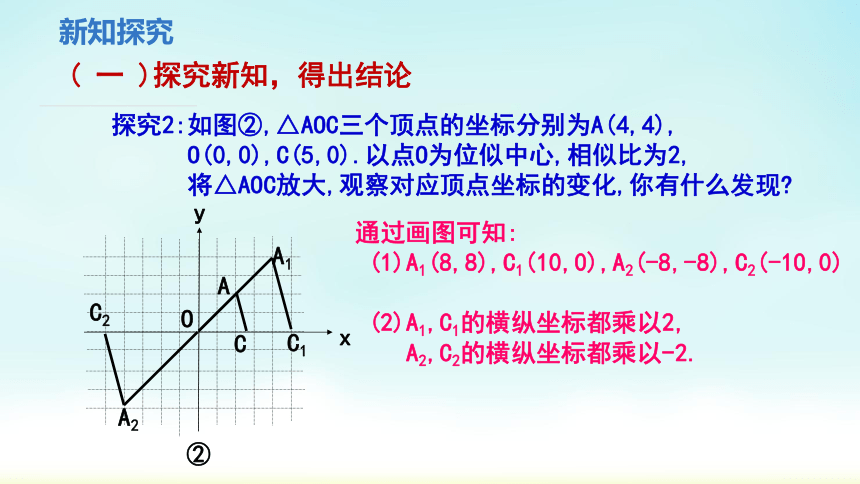
探究2:如图②,△AOC三个顶点的坐标分别为A(4,4),
O(0,0),C(5,0).以点O为位似中心,相似比为2,
将△AOC放大,观察对应顶点坐标的变化,你有什么发现
( 一 )探究新知,得出结论
A
A1
C
O
C1
C2
A2
y
x
②
通过画图可知:
(1)A1(8,8),C1(10,0),A2(-8,-8),C2(-10,0)
(2)A1,C1的横纵坐标都乘以2,
A2,C2的横纵坐标都乘以-2.
新知探究
结论:
一般地,在平面直角坐标系中,如果以原点为位似中心,
画出一个与原图形位似的图形,使它与原图形的相似比
为k,那么与原图形上的点(x,y)对应的位似图形上
的点的坐标为(kx,ky)或(-kx,-ky).
( 一 )探究新知,得出结论
新知探究
(二) 例题解析
例:如图③,△ABO三个顶点的坐标分别为A(-2,4),B(-2,0),
O(0,0).以原点O为位似中心,画出一个三角形,使它与
△ABO的相似比为3∶2.
③
O
A
B1
A1
B
x
y
新知探究
(二) 例题解析
思考:还有其他的画法吗?
④
B2
A2
O
B
A
x
y
课堂小结
结论:
一般地,在平面直角坐标系中,如果以原点为位似中心,
画出一个与原图形位似的图形,使它与原图形的相似比
为k,那么与原图形上的点(x,y)对应的位似图形上
的点的坐标为(kx,ky)或(-kx,-ky).
课堂训练
1.某个图形上各店的横纵坐标都变成原来的 ,连接各点
所得的图形与原图形相比( )
A.完全没有变化 B.扩大成原来的2倍
C.面积缩小为原来的 D.关于纵轴成轴对称
C
课堂训练
2.在平面直角坐标系中,已知点E(-4,2),F(-2,-2),以原点O为位似中心,
相似比为 ,把△EFO缩小,则点E的对应点E1的坐标为( )
A.(-2,1) B.(-8,4)
C.(-8,4)或(8,-4) D.(-2,1)或(2,-1)
D
课堂训练
3.如图⑤,线段AB两个端点的坐标分别为A(6,6),B(8,2),
以原点O为位似中心,在第一象限内,将线段AB缩小为原来的
后得到线段CD,则端点C的坐标为( )
A.(3,3) B.(4,3) C.(3,1) D.(4,1)
A
A
B
C
D
O
x
y
⑤
课堂训练
4.如图⑥,原点O是△ABC和△A1B1C1的位似中心,
点A(1,0),与点A1(-2,0)是对应点,△ABC的面积为 ,
则△A1B1C1的面积为( )
6
A
B
C
O
y
x
⑥
课堂训练
5.如图⑦,在△ABC中,A,B两个顶点在x轴的上方,点C的坐标为(-1,0),
以点C为位似中心,在x轴的下方作△ABC的位似图形,并把△ABC的
各边长放大到原来的2倍,记所得的图形为△A1B1C1,设点B的对应点
B1的横坐标为a,,则点B的横坐标为( )
D
y
x
A
B
A1
B1
C
O
⑦
第二十七章 相似
27.3 位似
第2课时
学习目标
1.让学生理解掌握位似图形在平面直角坐标系上的应用,
即会根据相似比,求位似图形的顶点,以及根据位似图形
对应点的坐标,求位似图形的相似比和在平面直角坐标系
中作出位似图形.
2.了解四种变化(平移,轴对称,旋转和位似)的异同,并能在
复杂的图形中找出这些变换.
新课导入
复习提问:
1.A(x,y)关于x轴对称的点的坐标是什么
2.A(x,y)关于y轴对称的点的坐标是什么
3.A(x,y)关于原点对称的点的坐标是什么
新知探究
( 一 )探究新知,得出结论
探究1:如图①,在直角坐标系中,有两点A(6,3),B(6,0).
以原点O为位似中心,相似比为1∶3,把线段AB缩小,
观察对应点之间坐标的变化,你有什么变化
①
A
B1
B2
A2
A1
B
y
x
通过画图可知:
(1)A1(2,1),B1(2,0),A2(-2,-1),B2(-2,0)
(2)A1,B1的横纵坐标都乘以 ,
A2,B2的横纵坐标都乘以 .
新知探究
探究2:如图②,△AOC三个顶点的坐标分别为A(4,4),
O(0,0),C(5,0).以点O为位似中心,相似比为2,
将△AOC放大,观察对应顶点坐标的变化,你有什么发现
( 一 )探究新知,得出结论
A
A1
C
O
C1
C2
A2
y
x
②
通过画图可知:
(1)A1(8,8),C1(10,0),A2(-8,-8),C2(-10,0)
(2)A1,C1的横纵坐标都乘以2,
A2,C2的横纵坐标都乘以-2.
新知探究
结论:
一般地,在平面直角坐标系中,如果以原点为位似中心,
画出一个与原图形位似的图形,使它与原图形的相似比
为k,那么与原图形上的点(x,y)对应的位似图形上
的点的坐标为(kx,ky)或(-kx,-ky).
( 一 )探究新知,得出结论
新知探究
(二) 例题解析
例:如图③,△ABO三个顶点的坐标分别为A(-2,4),B(-2,0),
O(0,0).以原点O为位似中心,画出一个三角形,使它与
△ABO的相似比为3∶2.
③
O
A
B1
A1
B
x
y
新知探究
(二) 例题解析
思考:还有其他的画法吗?
④
B2
A2
O
B
A
x
y
课堂小结
结论:
一般地,在平面直角坐标系中,如果以原点为位似中心,
画出一个与原图形位似的图形,使它与原图形的相似比
为k,那么与原图形上的点(x,y)对应的位似图形上
的点的坐标为(kx,ky)或(-kx,-ky).
课堂训练
1.某个图形上各店的横纵坐标都变成原来的 ,连接各点
所得的图形与原图形相比( )
A.完全没有变化 B.扩大成原来的2倍
C.面积缩小为原来的 D.关于纵轴成轴对称
C
课堂训练
2.在平面直角坐标系中,已知点E(-4,2),F(-2,-2),以原点O为位似中心,
相似比为 ,把△EFO缩小,则点E的对应点E1的坐标为( )
A.(-2,1) B.(-8,4)
C.(-8,4)或(8,-4) D.(-2,1)或(2,-1)
D
课堂训练
3.如图⑤,线段AB两个端点的坐标分别为A(6,6),B(8,2),
以原点O为位似中心,在第一象限内,将线段AB缩小为原来的
后得到线段CD,则端点C的坐标为( )
A.(3,3) B.(4,3) C.(3,1) D.(4,1)
A
A
B
C
D
O
x
y
⑤
课堂训练
4.如图⑥,原点O是△ABC和△A1B1C1的位似中心,
点A(1,0),与点A1(-2,0)是对应点,△ABC的面积为 ,
则△A1B1C1的面积为( )
6
A
B
C
O
y
x
⑥
课堂训练
5.如图⑦,在△ABC中,A,B两个顶点在x轴的上方,点C的坐标为(-1,0),
以点C为位似中心,在x轴的下方作△ABC的位似图形,并把△ABC的
各边长放大到原来的2倍,记所得的图形为△A1B1C1,设点B的对应点
B1的横坐标为a,,则点B的横坐标为( )
D
y
x
A
B
A1
B1
C
O
⑦
