人教版九年级数学下册 28-1-3 特殊角的锐角三角函数 (共13张ppt)
文档属性
| 名称 | 人教版九年级数学下册 28-1-3 特殊角的锐角三角函数 (共13张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-26 00:00:00 | ||
图片预览





文档简介
(共13张PPT)
第二十八章 锐角函数
28.1锐角三角函数
第3课时:特殊角的三角函数值
学习目标
能通过推理得30°,45°,60°角的锐角三角函数值,进一步体会三角
函数的意义。
2.会计算含有30°,45°,60°角的三角函数值。(重点)
3.能根据特殊角的三角函数值,说出相应锐角的大小。(难点)
4.经历探索30°,45°,60°角的三角函数值的过程,发展同学们
的推理能力和计算能力。
新课导入
复习提问:
1. 正弦,余弦,正切的定义分别是什么
2. 30°角的直角三角形的三边之比是什么
3. 45°角的直角三角形的三边之比是什么
新知探究
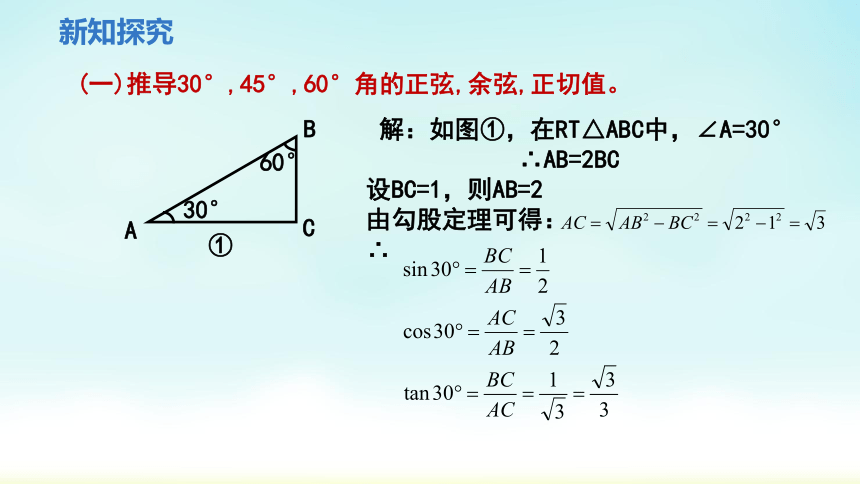
(一)推导30°,45°,60°角的正弦,余弦,正切值。
B
A
60°
C
30°
①
解:如图①,在RT△ABC中,∠A=30°
∴AB=2BC
设BC=1,则AB=2
由勾股定理可得:
∴
新知探究
(一)推导30°,45°,60°角的正弦,余弦,正切值。
B
A
60°
C
30°
①
解:如图①,在RT△ABC中,∠A=30°
∴AB=2BC
设BC=1,则AB=2
由勾股定理可得:
∴
新知探究
(一)推导30°,45°,60°角的正弦,余弦,正切值。
B
45°
C
A
②
解: 如图②,
在RT△ABC中,∠A=45°,则AC=BC
设AC=BC=1
由勾股定理可得:
∴
新知探究
总结:特殊角的三角函数值
30° 45°
60°
sinA
cosA
tanA
新知探究
(二)例题解析,新知应用
例3:求下列各式的值。
(1)
(2)
解:(1)
(2)
新知探究
(二)例题解析,新知应用
例4: (1)如图③,在RT△ABC中,∠C=90°,
求∠A的度数.
B
③
C
A
解:(1)在图③中
新知探究
(二)例题解析,新知应用
例4: (2)如图④,AO是圆锥的高,OB是底面半径, ,
求α的度数.
O
A
α
B
④
解:(1)在图④中,
课堂小结
1.特殊角的三角函数值
30° 45°
60°
sinA
cosA
tanA
2.根据函数值确定角的度数.
课堂训练
1.如果α是等边三角形的一个内角,那么cosα的值为( )
A B C D 1
A
2.如果在△ABC中, ,则下列最确切的结论是( )
A △ABC是直角三角形 B △ABC是等腰三角形
C △ABC是等腰直角三角形 D △ABC是锐角三角形
C
课堂训练
3.在△ABC中,∠A,∠B都是锐角,且 ,则△ABC的形状是( )
A 直角三角形 B 钝角三角形 C 锐角三角形 D 不能确定
B
4. 的值是( )
5. 已知α是锐角,且 ,则α=( )
45°
第二十八章 锐角函数
28.1锐角三角函数
第3课时:特殊角的三角函数值
学习目标
能通过推理得30°,45°,60°角的锐角三角函数值,进一步体会三角
函数的意义。
2.会计算含有30°,45°,60°角的三角函数值。(重点)
3.能根据特殊角的三角函数值,说出相应锐角的大小。(难点)
4.经历探索30°,45°,60°角的三角函数值的过程,发展同学们
的推理能力和计算能力。
新课导入
复习提问:
1. 正弦,余弦,正切的定义分别是什么
2. 30°角的直角三角形的三边之比是什么
3. 45°角的直角三角形的三边之比是什么
新知探究
(一)推导30°,45°,60°角的正弦,余弦,正切值。
B
A
60°
C
30°
①
解:如图①,在RT△ABC中,∠A=30°
∴AB=2BC
设BC=1,则AB=2
由勾股定理可得:
∴
新知探究
(一)推导30°,45°,60°角的正弦,余弦,正切值。
B
A
60°
C
30°
①
解:如图①,在RT△ABC中,∠A=30°
∴AB=2BC
设BC=1,则AB=2
由勾股定理可得:
∴
新知探究
(一)推导30°,45°,60°角的正弦,余弦,正切值。
B
45°
C
A
②
解: 如图②,
在RT△ABC中,∠A=45°,则AC=BC
设AC=BC=1
由勾股定理可得:
∴
新知探究
总结:特殊角的三角函数值
30° 45°
60°
sinA
cosA
tanA
新知探究
(二)例题解析,新知应用
例3:求下列各式的值。
(1)
(2)
解:(1)
(2)
新知探究
(二)例题解析,新知应用
例4: (1)如图③,在RT△ABC中,∠C=90°,
求∠A的度数.
B
③
C
A
解:(1)在图③中
新知探究
(二)例题解析,新知应用
例4: (2)如图④,AO是圆锥的高,OB是底面半径, ,
求α的度数.
O
A
α
B
④
解:(1)在图④中,
课堂小结
1.特殊角的三角函数值
30° 45°
60°
sinA
cosA
tanA
2.根据函数值确定角的度数.
课堂训练
1.如果α是等边三角形的一个内角,那么cosα的值为( )
A B C D 1
A
2.如果在△ABC中, ,则下列最确切的结论是( )
A △ABC是直角三角形 B △ABC是等腰三角形
C △ABC是等腰直角三角形 D △ABC是锐角三角形
C
课堂训练
3.在△ABC中,∠A,∠B都是锐角,且 ,则△ABC的形状是( )
A 直角三角形 B 钝角三角形 C 锐角三角形 D 不能确定
B
4. 的值是( )
5. 已知α是锐角,且 ,则α=( )
45°
