人教版九年级数学下册 28-2-1 解直角三角形 (共18张ppt)
文档属性
| 名称 | 人教版九年级数学下册 28-2-1 解直角三角形 (共18张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-26 21:23:33 | ||
图片预览





文档简介
(共18张PPT)
第二十八章 锐角三角函数
28.2.1解直角三角形
学习目标
1. 使学生理解直角三角形中五个元素的关系,会运用勾股定理,
直角三角形的两个锐角互余及锐角三角函数解直角三角形.
通过综合运用勾股定理,直角三角形的两个锐角互余及锐角三角函数
解直角三角形,逐步培养学生分析问题,解决问题的能力.
3. 渗透数形结合的数学思想,培养学生良好的学习习惯.
新课导入
复习提问:
1.正弦,余弦,正切的定义分别是什么
2.一个三角形有几个元素
3.在RT△ABC中,∠C=90°,那么a,b,c,∠A,∠B之间有什么的等量关系
A
c
b
B
a
C
①
(1)三边之间的关系: (勾股定理)
(2)两锐角之间的关系:∠A+∠B=90°
(3)边角之间的关系:
新课导入
复习提问:
4.解直角三角形定义:
5.分析直角三角形五个元素之间的关系,为什么已知的两个条件中
至少有一条是边呢 思考如果仅仅已知两个锐角,可以解直角三
角形吗
由直角三角形的已知元素,求出其余未知元素的过程,叫做解直角三角形.
新知探究
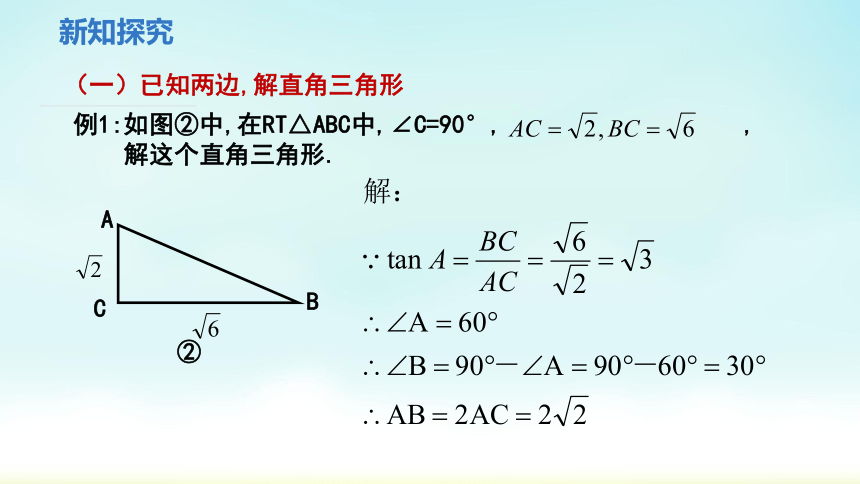
(一)已知两边,解直角三角形
B
A
C
②
例1:如图②中,在RT△ABC中,∠C=90°, ,
解这个直角三角形.
新知探究
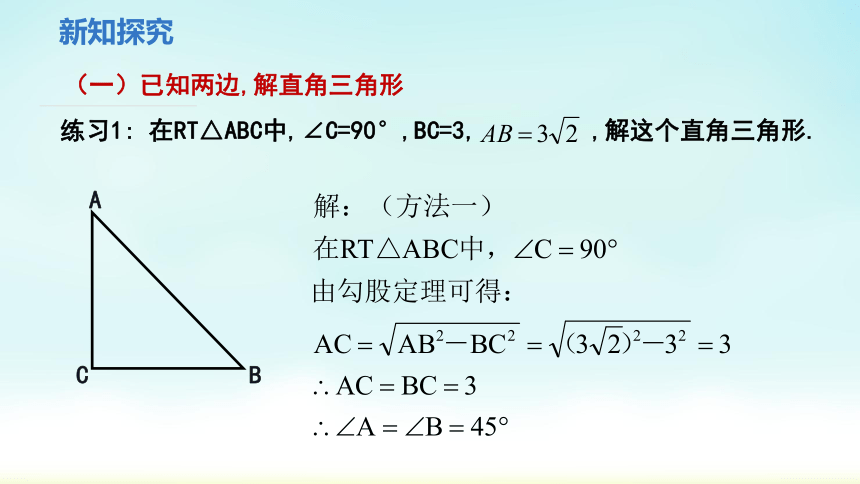
(一)已知两边,解直角三角形
练习1: 在RT△ABC中,∠C=90°,BC=3, ,解这个直角三角形.
C
A
B
新知探究
(一)已知两边,解直角三角形
练习1: 在RT△ABC中,∠C=90°,BC=3, ,解这个直角三角形.
C
A
B
思考:含有其他方法吗
新知探究
总结:(一)已知两边,解直角三角形
已知类型 已知条件
解法步骤
两边 斜边和一直角边(如c,a) ①
②
③∠B=90°-∠A
两直角边(如a,b) ①
②
③∠B=90°-∠A
新知探究
(二)已知一边和一锐角,解直角三角形
例2:如图③,在RT△ABC中,∠C=90°,∠B=35°,b=20 ,
解这个直角三角形(结果保留小数点后一位)。
A
c
b=20
B
35°
a
C
③
新知探究
(二)已知一边和一锐角,解直角三角形
练习2:如图④中,在RT△ABC中,∠C=90°,AC=10,∠A=30°,
解这个直角三角形.
A
B
C
④
新知探究
(二)已知一边和一锐角,解直角三角形
练习2:如图④中,在RT△ABC中,∠C=90°,AC=10,∠A=30°,
解这个直角三角形.
A
B
C
④
思考:含有其他方法吗
新知探究
总结:(二)已知一边和一锐角,解直角三角形
已知类型 已知条件
解法步骤
一边和一锐角 斜边和一锐角(如c,∠A) ①∠B=90°-∠A
②
③
一直角边和一锐角(如a,∠A) ①∠B=90°-∠A
②
③
课堂小结
A
c
b
B
a
C
①
(1)三边之间的关系: (勾股定理)
(3)边角之间的关系:
(2)两锐角之间的关系:∠A+∠B=90°
1.直角三角形的五个元素关系:
课堂小结
(一)已知两边,解直角三角形
已知类型 已知条件
解法步骤
两边 斜边和一直角边(如c,a) ①
②
③∠B=90°-∠A
两直角边(如a,b) ①
②
③∠B=90°-∠A
课堂小结
(二)已知一边和一锐角,解直角三角形
已知类型 已知条件
解法步骤
一边和一锐角 斜边和一锐角(如c,∠A) ①∠B=90°-∠A
②
③
一直角边和一锐角(如a,∠A) ①∠B=90°-∠A
②
③
课堂训练
1.在△ABC中,∠C=90°,AC=6,BC=8,那么sinA=( )
2.在△ABC中,∠C=90°, ,则cosA的值是( )
A B C D
B
课堂训练
A
B
C
⑤
A
m
C
α
B
⑥
A
4.如图⑥中,小明为了测量其所在位置A点到河对岸B点之间的距离,
沿着与AB垂直的方向走了m米,到达点C,测得∠ACB=α,那么AB等于( )
A B C D
B
3.如图⑤中,已知RT△ABC中,∠C=90°,AC=4, ,
则BC的长为( )
A 2 B 8 C D
课堂训练
6.如图⑧中,菱形ABCD中,DE⊥AB于点E, ,BE=4,则
DE的值为( )
5.如图⑦中,已知在RT△ABC中,斜边BC上的高AD=3,
则AC等于( )
A
B
D
C
⑦
D
C
A
E
B
⑧
8
第二十八章 锐角三角函数
28.2.1解直角三角形
学习目标
1. 使学生理解直角三角形中五个元素的关系,会运用勾股定理,
直角三角形的两个锐角互余及锐角三角函数解直角三角形.
通过综合运用勾股定理,直角三角形的两个锐角互余及锐角三角函数
解直角三角形,逐步培养学生分析问题,解决问题的能力.
3. 渗透数形结合的数学思想,培养学生良好的学习习惯.
新课导入
复习提问:
1.正弦,余弦,正切的定义分别是什么
2.一个三角形有几个元素
3.在RT△ABC中,∠C=90°,那么a,b,c,∠A,∠B之间有什么的等量关系
A
c
b
B
a
C
①
(1)三边之间的关系: (勾股定理)
(2)两锐角之间的关系:∠A+∠B=90°
(3)边角之间的关系:
新课导入
复习提问:
4.解直角三角形定义:
5.分析直角三角形五个元素之间的关系,为什么已知的两个条件中
至少有一条是边呢 思考如果仅仅已知两个锐角,可以解直角三
角形吗
由直角三角形的已知元素,求出其余未知元素的过程,叫做解直角三角形.
新知探究
(一)已知两边,解直角三角形
B
A
C
②
例1:如图②中,在RT△ABC中,∠C=90°, ,
解这个直角三角形.
新知探究
(一)已知两边,解直角三角形
练习1: 在RT△ABC中,∠C=90°,BC=3, ,解这个直角三角形.
C
A
B
新知探究
(一)已知两边,解直角三角形
练习1: 在RT△ABC中,∠C=90°,BC=3, ,解这个直角三角形.
C
A
B
思考:含有其他方法吗
新知探究
总结:(一)已知两边,解直角三角形
已知类型 已知条件
解法步骤
两边 斜边和一直角边(如c,a) ①
②
③∠B=90°-∠A
两直角边(如a,b) ①
②
③∠B=90°-∠A
新知探究
(二)已知一边和一锐角,解直角三角形
例2:如图③,在RT△ABC中,∠C=90°,∠B=35°,b=20 ,
解这个直角三角形(结果保留小数点后一位)。
A
c
b=20
B
35°
a
C
③
新知探究
(二)已知一边和一锐角,解直角三角形
练习2:如图④中,在RT△ABC中,∠C=90°,AC=10,∠A=30°,
解这个直角三角形.
A
B
C
④
新知探究
(二)已知一边和一锐角,解直角三角形
练习2:如图④中,在RT△ABC中,∠C=90°,AC=10,∠A=30°,
解这个直角三角形.
A
B
C
④
思考:含有其他方法吗
新知探究
总结:(二)已知一边和一锐角,解直角三角形
已知类型 已知条件
解法步骤
一边和一锐角 斜边和一锐角(如c,∠A) ①∠B=90°-∠A
②
③
一直角边和一锐角(如a,∠A) ①∠B=90°-∠A
②
③
课堂小结
A
c
b
B
a
C
①
(1)三边之间的关系: (勾股定理)
(3)边角之间的关系:
(2)两锐角之间的关系:∠A+∠B=90°
1.直角三角形的五个元素关系:
课堂小结
(一)已知两边,解直角三角形
已知类型 已知条件
解法步骤
两边 斜边和一直角边(如c,a) ①
②
③∠B=90°-∠A
两直角边(如a,b) ①
②
③∠B=90°-∠A
课堂小结
(二)已知一边和一锐角,解直角三角形
已知类型 已知条件
解法步骤
一边和一锐角 斜边和一锐角(如c,∠A) ①∠B=90°-∠A
②
③
一直角边和一锐角(如a,∠A) ①∠B=90°-∠A
②
③
课堂训练
1.在△ABC中,∠C=90°,AC=6,BC=8,那么sinA=( )
2.在△ABC中,∠C=90°, ,则cosA的值是( )
A B C D
B
课堂训练
A
B
C
⑤
A
m
C
α
B
⑥
A
4.如图⑥中,小明为了测量其所在位置A点到河对岸B点之间的距离,
沿着与AB垂直的方向走了m米,到达点C,测得∠ACB=α,那么AB等于( )
A B C D
B
3.如图⑤中,已知RT△ABC中,∠C=90°,AC=4, ,
则BC的长为( )
A 2 B 8 C D
课堂训练
6.如图⑧中,菱形ABCD中,DE⊥AB于点E, ,BE=4,则
DE的值为( )
5.如图⑦中,已知在RT△ABC中,斜边BC上的高AD=3,
则AC等于( )
A
B
D
C
⑦
D
C
A
E
B
⑧
8
