人教版九年级数学下册 28.2.2 第1课时 与视角有关的应用题 课件(18张ppt)
文档属性
| 名称 | 人教版九年级数学下册 28.2.2 第1课时 与视角有关的应用题 课件(18张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-27 07:47:03 | ||
图片预览



文档简介
(共18张PPT)
第二十八章 锐角三角函数
28.2.2应用举例
第一课时:与视角有关的实际应用
学习目标
1.理解仰角,俯角的概念,把实际问题抽象成几何图形,解决问题。
2.能利用锐角三角函数的知识解决实际问题。
新课导入
复习提问:
1.直角三角形三边之间的关系是什么?
2.直角三角形两锐角的关系是什么?
3.直角三角形边与角之间的关系是什么?
4.仰角,俯角分别是什么
新知探究
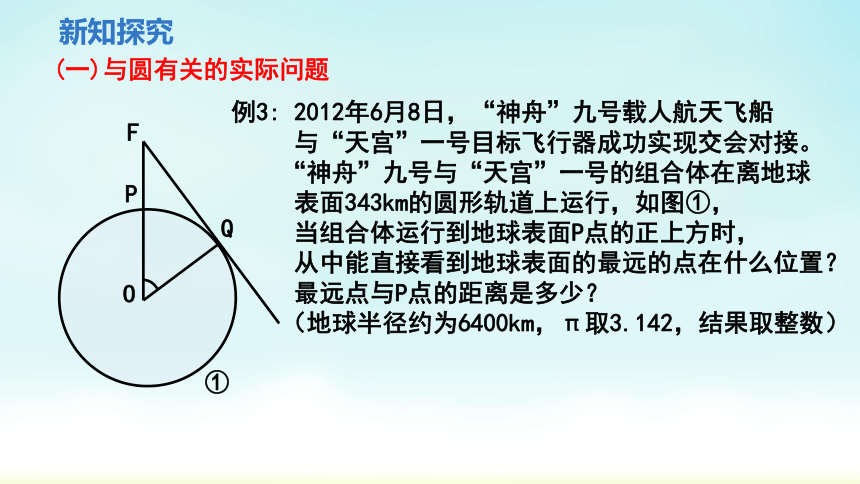
例3: 2012年6月8日,“神舟”九号载人航天飞船
与“天宫”一号目标飞行器成功实现交会对接。
“神舟”九号与“天宫”一号的组合体在离地球
表面343km的圆形轨道上运行,如图①,
当组合体运行到地球表面P点的正上方时,
从中能直接看到地球表面的最远的点在什么位置?
最远点与P点的距离是多少?
(地球半径约为6400km,π取3.142,结果取整数)
F
P
Q
O
①
(一)与圆有关的实际问题
新知探究
(一)与圆有关的实际问题
F
P
Q
O
①
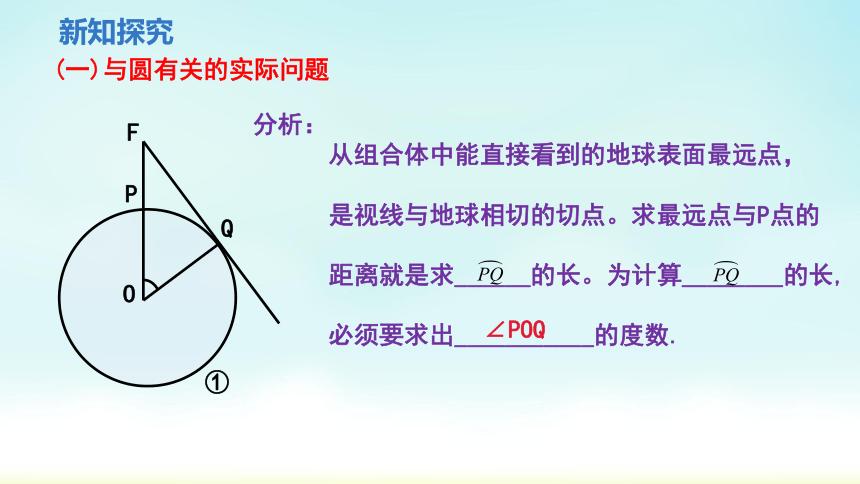
分析:
从组合体中能直接看到的地球表面最远点,
是视线与地球相切的切点。求最远点与P点的
距离就是求______的长。为计算________的长,
必须要求出___________的度数.
∠POQ
新知探究
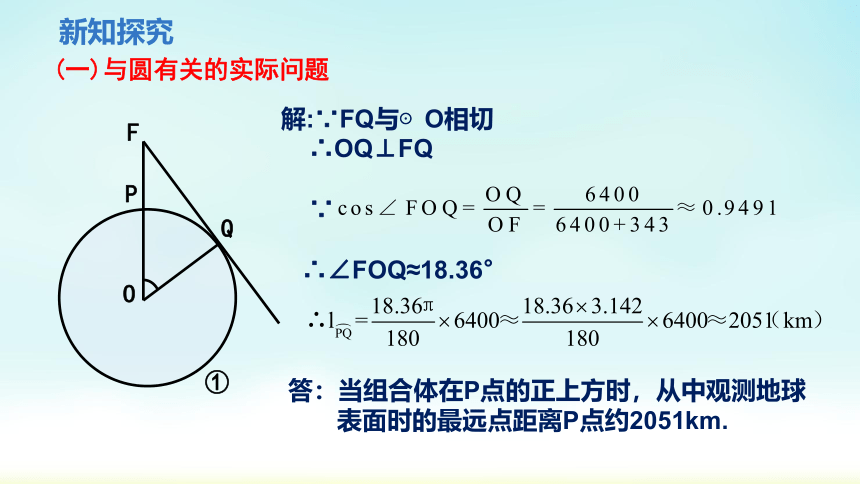
解:∵FQ与⊙O相切
∴OQ⊥FQ
∵
∴∠FOQ≈18.36°
答:当组合体在P点的正上方时,从中观测地球
表面时的最远点距离P点约2051km.
F
P
Q
O
①
(一)与圆有关的实际问题
新知探究
(二)与视角有关的实际问题
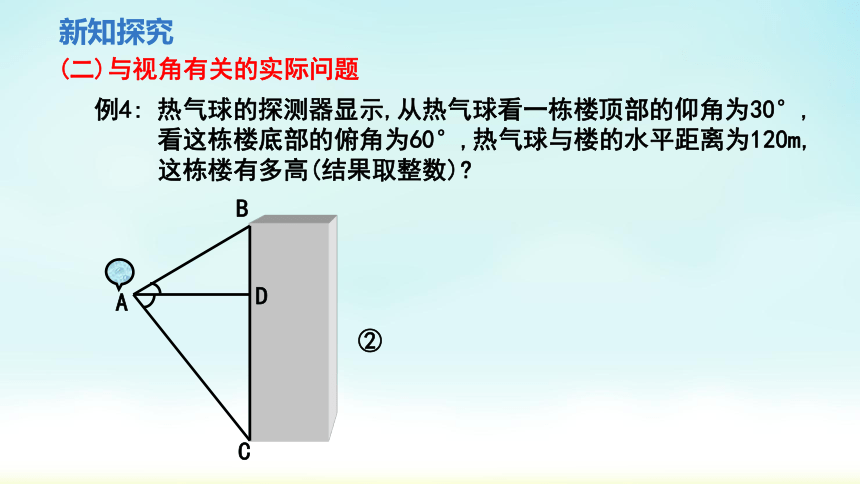
例4: 热气球的探测器显示,从热气球看一栋楼顶部的仰角为30°,
看这栋楼底部的俯角为60°,热气球与楼的水平距离为120m,
这栋楼有多高(结果取整数)
A
B
D
C
②
新知探究
A
B
D
C
②
(二)与视角有关的实际问题
分析:
1.视线与水平线所成的角中,视线在水平线
上方的是仰角,视线在水平线下方的是俯角
(如图③)。所以在图②中,∠BAD为仰角,
∠CAD为俯角,由此可知∠BAD=30°,∠CAD=60°.
视线
铅
垂线
仰角
水平线
俯角
视线
③
2.要求CB就要求出BD和CD的长。在RT△ABD中利用
tan∠BAD求出BD,在RT△ACD中利用tan∠CAD
求出CD即可。
新知探究
A
B
D
C
②
(二)与视角有关的实际问题
解:如图②,∠BAD=30°,∠CAD=60°,AD=120°
答:这栋楼的高约为277米.
新知探究
(二)与视角有关的实际问题
例4: 如图③,某人为了测量小山顶上的塔ED的高,他在山下
的点A处测得塔尖点D的仰角为45°,再沿AC方向前进60m,
到达山脚的点B处,测得塔尖点D的仰角为60°,塔底点E的
仰角为30°,求塔ED的高度(结果保留根号)
1
A
B
D
E
C
③
2
新知探究
1
A
B
D
E
C
③
2
(二)与视角有关的实际问题
解:
思考:你能在图中通过设其他边长
求出塔高DE吗?请比较各种
方法,总结怎样设未知数会
使运算比较简单。
课堂小结
解决有关仰角,俯角的实际问题的方法:
① 仰角和俯角是指视线与水平线的夹角,上仰下俯。
② 解答有关仰角俯角的问题关键是弄清仰角和俯角的
定义,根据题意画出几何图形,将实际问题中的数量
关系归结到直角三角形中来求解。
③ 若有两个或两个以上的三角形,不能直接解出的,
可以考虑分别由两个三角形找出含有相同未知元素
的关系式,运用方程知识求解。
课堂训练
D
45°
C
A
D
B
30°
④
1.如图④,从热气球C处测得地面A,B两点的俯角分别为30°,45°,
如果此时热气球C处的高度CD为100米,点A, D,B在同一直线上,
则A,B两点的距离是( )
A.200米 B. C. D.
课堂训练
D
2. 如图⑤,某同学用一个有30°角的直角三角板估测他们学校
的旗杆AB的高度.他将30°角的直角边水平放在1.5米高的支架
CD上,三角板的斜边与旗杆的顶点在同一直线上,他又量得DB
的距离为10米,则旗杆AB的高度为( )
A. B. C. D.
30°
A
C
E
D
B
⑤
课堂训练
3.如图⑥,某飞机在空中A处探测到地平面目标B,此时从飞机上看
目标B的俯角α=30°,飞行高度AC=1200m,则飞机到目标B的距离
AB为( )
A.1200m B.2400m C. D.
B
A
α
C
B
⑥
课堂训练
4.如图⑦,创新小组要测量公园内一棵树的高度AB,其中一名小组
成员站在距离树10m的点E处,测得树顶A的仰角为60°,已知测角仪
的架高CE=1.5m,在这棵树的高度为___________米.(保留根号)
⑦
60°
C
A
E
B
D
课堂训练
5.如图⑧,某人站在楼顶观测对面笔直的旗杆AB,测得旗杆顶的
仰角∠ECA=30°,CE=BD=8m,旗杆底部的俯角∠ECB=45°,
那么旗杆AB的高度是( )
A. B. C. D.
A
E
C
B
D
⑧
D
课堂训练
A
6.某水库大坝横断面如图⑨所示,其中CD,AB分别表示水库上下底面
的水平线,∠ABC=120°,BC的长是50m,则水库大坝的高度h为( )
A. B.25m C. D.
A
B
C
D
⑨
120°
h
第二十八章 锐角三角函数
28.2.2应用举例
第一课时:与视角有关的实际应用
学习目标
1.理解仰角,俯角的概念,把实际问题抽象成几何图形,解决问题。
2.能利用锐角三角函数的知识解决实际问题。
新课导入
复习提问:
1.直角三角形三边之间的关系是什么?
2.直角三角形两锐角的关系是什么?
3.直角三角形边与角之间的关系是什么?
4.仰角,俯角分别是什么
新知探究
例3: 2012年6月8日,“神舟”九号载人航天飞船
与“天宫”一号目标飞行器成功实现交会对接。
“神舟”九号与“天宫”一号的组合体在离地球
表面343km的圆形轨道上运行,如图①,
当组合体运行到地球表面P点的正上方时,
从中能直接看到地球表面的最远的点在什么位置?
最远点与P点的距离是多少?
(地球半径约为6400km,π取3.142,结果取整数)
F
P
Q
O
①
(一)与圆有关的实际问题
新知探究
(一)与圆有关的实际问题
F
P
Q
O
①
分析:
从组合体中能直接看到的地球表面最远点,
是视线与地球相切的切点。求最远点与P点的
距离就是求______的长。为计算________的长,
必须要求出___________的度数.
∠POQ
新知探究
解:∵FQ与⊙O相切
∴OQ⊥FQ
∵
∴∠FOQ≈18.36°
答:当组合体在P点的正上方时,从中观测地球
表面时的最远点距离P点约2051km.
F
P
Q
O
①
(一)与圆有关的实际问题
新知探究
(二)与视角有关的实际问题
例4: 热气球的探测器显示,从热气球看一栋楼顶部的仰角为30°,
看这栋楼底部的俯角为60°,热气球与楼的水平距离为120m,
这栋楼有多高(结果取整数)
A
B
D
C
②
新知探究
A
B
D
C
②
(二)与视角有关的实际问题
分析:
1.视线与水平线所成的角中,视线在水平线
上方的是仰角,视线在水平线下方的是俯角
(如图③)。所以在图②中,∠BAD为仰角,
∠CAD为俯角,由此可知∠BAD=30°,∠CAD=60°.
视线
铅
垂线
仰角
水平线
俯角
视线
③
2.要求CB就要求出BD和CD的长。在RT△ABD中利用
tan∠BAD求出BD,在RT△ACD中利用tan∠CAD
求出CD即可。
新知探究
A
B
D
C
②
(二)与视角有关的实际问题
解:如图②,∠BAD=30°,∠CAD=60°,AD=120°
答:这栋楼的高约为277米.
新知探究
(二)与视角有关的实际问题
例4: 如图③,某人为了测量小山顶上的塔ED的高,他在山下
的点A处测得塔尖点D的仰角为45°,再沿AC方向前进60m,
到达山脚的点B处,测得塔尖点D的仰角为60°,塔底点E的
仰角为30°,求塔ED的高度(结果保留根号)
1
A
B
D
E
C
③
2
新知探究
1
A
B
D
E
C
③
2
(二)与视角有关的实际问题
解:
思考:你能在图中通过设其他边长
求出塔高DE吗?请比较各种
方法,总结怎样设未知数会
使运算比较简单。
课堂小结
解决有关仰角,俯角的实际问题的方法:
① 仰角和俯角是指视线与水平线的夹角,上仰下俯。
② 解答有关仰角俯角的问题关键是弄清仰角和俯角的
定义,根据题意画出几何图形,将实际问题中的数量
关系归结到直角三角形中来求解。
③ 若有两个或两个以上的三角形,不能直接解出的,
可以考虑分别由两个三角形找出含有相同未知元素
的关系式,运用方程知识求解。
课堂训练
D
45°
C
A
D
B
30°
④
1.如图④,从热气球C处测得地面A,B两点的俯角分别为30°,45°,
如果此时热气球C处的高度CD为100米,点A, D,B在同一直线上,
则A,B两点的距离是( )
A.200米 B. C. D.
课堂训练
D
2. 如图⑤,某同学用一个有30°角的直角三角板估测他们学校
的旗杆AB的高度.他将30°角的直角边水平放在1.5米高的支架
CD上,三角板的斜边与旗杆的顶点在同一直线上,他又量得DB
的距离为10米,则旗杆AB的高度为( )
A. B. C. D.
30°
A
C
E
D
B
⑤
课堂训练
3.如图⑥,某飞机在空中A处探测到地平面目标B,此时从飞机上看
目标B的俯角α=30°,飞行高度AC=1200m,则飞机到目标B的距离
AB为( )
A.1200m B.2400m C. D.
B
A
α
C
B
⑥
课堂训练
4.如图⑦,创新小组要测量公园内一棵树的高度AB,其中一名小组
成员站在距离树10m的点E处,测得树顶A的仰角为60°,已知测角仪
的架高CE=1.5m,在这棵树的高度为___________米.(保留根号)
⑦
60°
C
A
E
B
D
课堂训练
5.如图⑧,某人站在楼顶观测对面笔直的旗杆AB,测得旗杆顶的
仰角∠ECA=30°,CE=BD=8m,旗杆底部的俯角∠ECB=45°,
那么旗杆AB的高度是( )
A. B. C. D.
A
E
C
B
D
⑧
D
课堂训练
A
6.某水库大坝横断面如图⑨所示,其中CD,AB分别表示水库上下底面
的水平线,∠ABC=120°,BC的长是50m,则水库大坝的高度h为( )
A. B.25m C. D.
A
B
C
D
⑨
120°
h
