2021-2022学年北师大版八年级数学上册第五章二元一次方程组期末复习提升训练1(Word版,附答案解析)
文档属性
| 名称 | 2021-2022学年北师大版八年级数学上册第五章二元一次方程组期末复习提升训练1(Word版,附答案解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 200.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-26 00:00:00 | ||
图片预览



文档简介
2021-2022学年北师大版八年级数学上册《第5章二元一次方程组》
期末复习提升训练1(附答案)
1.下列四个方程组中,是二元一次方程组的有( )个.
(1),(2)(3)(4).
A.4 B.3 C.2 D.1
2.若是关于x、y的方程组的一个解,则的a+b值为( )
A.0 B.﹣1 C.1 D.﹣2
3.关于x,y的二元一次方程组中,m与方程组的解中的x或y相等,则m的值为( )
A.3或 B.2或﹣ C.3或 D.2或﹣
4.若x2m+ny与x5ym﹣n是同类项,则m,n的值是( )
A.m=2、n=3 B.m=2、n=1 C.m=2、n=0 D.m=1、n=2
5.如果直线y=3x+6与y=2x﹣4交点坐标为(a,b),则是下列哪个方程组的解( )
A. B.
C. D.
6.端午节前夕,某超市用1680元购进A、B两种商品共60件,其中A型商品每件24元,B型商品每件36元.设购买A型商品x件、B型商品y件,依题意列方程组正确的是( )
A. B.
C. D.
7.一个两位数,十位上的数与个位上的数的和是7,若十位上的数与个位上的数对换,得到的两位数与原来的两位数的差是9,则现在的两位数是( )
A.43 B.34 C.25 D.52
8.等腰三角形的周长为15,其中一边长为3,则该等腰三角形的底边长为( )
A.3 B.4 C.5 D.6
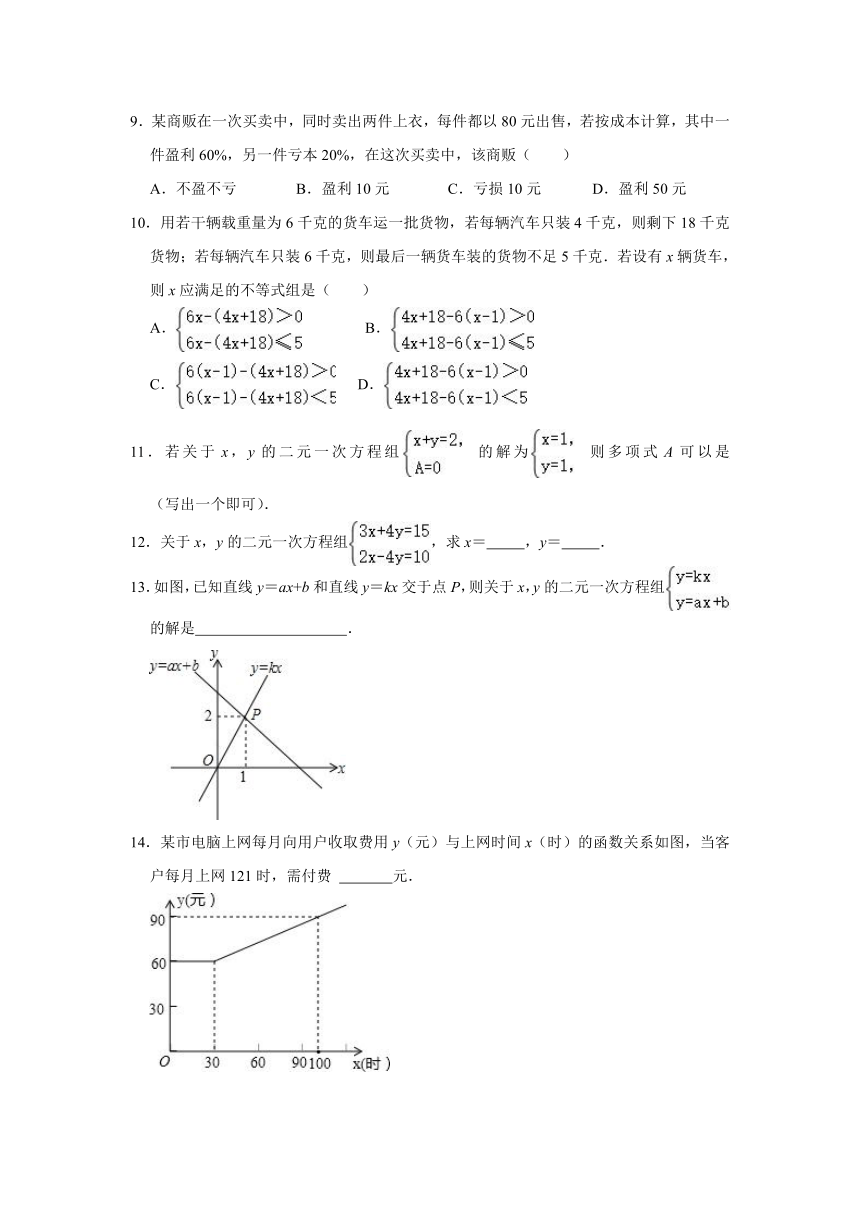
9.某商贩在一次买卖中,同时卖出两件上衣,每件都以80元出售,若按成本计算,其中一件盈利60%,另一件亏本20%,在这次买卖中,该商贩( )
A.不盈不亏 B.盈利10元 C.亏损10元 D.盈利50元
10.用若干辆载重量为6千克的货车运一批货物,若每辆汽车只装4千克,则剩下18千克货物;若每辆汽车只装6千克,则最后一辆货车装的货物不足5千克.若设有x辆货车,则x应满足的不等式组是( )
A. B.
C. D.
11.若关于x,y的二元一次方程组的解为则多项式A可以是 (写出一个即可).
12.关于x,y的二元一次方程组,求x= ,y= .
13.如图,已知直线y=ax+b和直线y=kx交于点P,则关于x,y的二元一次方程组的解是 .
14.某市电脑上网每月向用户收取费用y(元)与上网时间x(时)的函数关系如图,当客户每月上网121时,需付费 元.
15.一个两位数,两个数位上的数字一个是另一个的2倍,若把此两位数的两个数字对调,所得新数比原数大27,则此两位数是 .
16.“双11”促销活动中,小芳的妈妈计划用100元在唯品会购买价格分别为8元和12元的两种商品,则可供小芳妈妈选择的购买方案有 种.
17.已知是方程组的解,则m+n= .
18.已知直线y=x﹣1与y=﹣x+5的交点坐标是(4,1),则方程组的解是 .
19.已知方程组与方程组的解相同,求a、b的值.
20.某市火车站北广场将于2021年底投入使用,计划在广场内种植A,B两种花木共6600棵,若A花木数量是B花木数量的2倍少600棵.
(1)A,B两种花木的数量分别是多少棵?
(2)如果园林处安排13人同时种植这两种花木,每人每天能种植A花木60棵或B花木40棵,应分别安排多少人种植A花木和B花木,才能确保同时完成各自的任务?
21.解方程组.
22.根据下列条件,分别确定一次函数的解析式:
(1)图象过P(﹣1,﹣2),Q(﹣3,4);
(2)直线y=kx+b与直线y=﹣2x+3平行,且过点(4,6).
23.请用两种方法解答下面的应用题:
在一个房间里有四条腿的椅子和三条腿的凳子共16个,如果椅子腿和凳子腿数加起来共有60个,有几个椅子和几个凳子?
24.一辆汽车从A地驶往B地,前路段为普通公路,其余路段为高速公路.已知汽车在普通公路上行驶的速度为60km/h,在高速公路上行驶的速度为100km/h,汽车从A地到B地一共行驶了2.2h.
请你根据以上信息,就该汽车行驶的“路程”或“时间”,提出一个用二元一次方程组解决的问题,并写出解答过程.
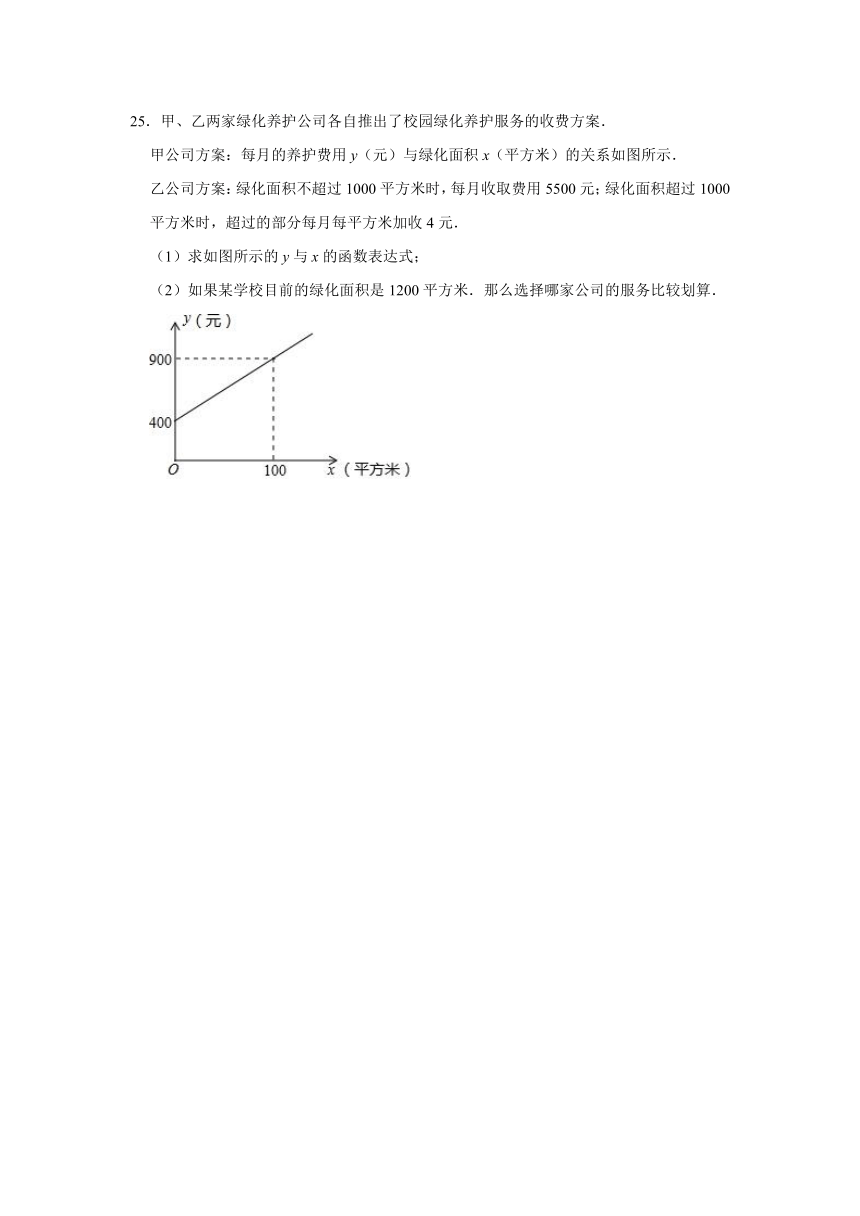
25.甲、乙两家绿化养护公司各自推出了校园绿化养护服务的收费方案.
甲公司方案:每月的养护费用y(元)与绿化面积x(平方米)的关系如图所示.
乙公司方案:绿化面积不超过1000平方米时,每月收取费用5500元;绿化面积超过1000平方米时,超过的部分每月每平方米加收4元.
(1)求如图所示的y与x的函数表达式;
(2)如果某学校目前的绿化面积是1200平方米.那么选择哪家公司的服务比较划算.
参考答案
1.解:(1)是二元二次方程组;
(2)是二元二次方程组;
(3)是分式,不是二元一次方程组;
(4)是二元一次方程组;
故选:D.
2.解:把代入方程组得:,
①+②得:a+b=﹣1,
故选:B.
3.解:若m=x,方程组变形为,
解得:,此时m=x=2;
若m=y,方程组变形为,
解得:,此时m=y=﹣,
则m的值为2或﹣,
故选:D.
4.解:∵x2m+ny与x5ym﹣n是同类项,
∴,
①+②得:3m=6,即m=2,
把m=2代入②得:n=1,
故选:B.
5.解:∵直线y=3x+6与y=2x﹣4交点坐标为(a,b),
∴解为的方程组是,
即,
故选:A.
6.解:设购买A型商品x件、B型商品y件,依题意列方程组:
.
故选:B.
7.解:设原来的两位数个位上的数是x,十位上的数是y,
根据题意得,10x+y﹣(10y+x)=9,
解得:x=4,y=3,
答案为43,
故选:A.
8.解:若腰长为3,则底边长为:15﹣3﹣3=9,
∵3+3<9,
∴不能组成三角形,舍去;
若底边长为3,则腰长为:=6;
∴该等腰三角形的底边长为:3;
故选:A.
9.解:设盈利60%的衣服的成本为x元,则x×(1+60%)=80,
解得x=50,
设亏损20%的衣服的成本为y元,y×(1﹣20%)=80,
解得y=100元,
∴总成本为100+50=150元,
∴2×80﹣150=10,
∴这次买卖中他是盈利10元.
故选:B.
10.解:设有x辆货车,
每辆汽车只装4千克,则剩下18千克货物,
所以,货物总重为(4x+18)千克,
每辆汽车只装6千克,则最后一辆货车装的货物不足5千克,
根据等量关系,可得到不等式为:
4x+18﹣6(x﹣1)<5和4x+18﹣6(x﹣1)>0.
故选:D.
11.解:∵关于x,y的二元一次方程组的解为,
而1﹣1=0,
∴多项式A可以是答案不唯一,如x﹣y.
故答案为:答案不唯一,如x﹣y.
12.解:,
①+②,得5x=25,解得x=5,
把x=5代入①,得15+4y=15,解得y=0,
所以方程组的解为.
故答案为:5;0.
13.解:∵直线y=ax+b和直线y=kx交点P的坐标为(1,2),
∴关于x,y的二元一次方程组的解为.
故答案为.
14.解:设后段的解析式为y=kx+b,由图象过点(30,60),(100,90)得,解之得,
所以函数解析式为y=,当x=121时y=99,即此时需付费99元.
15.解:设十位数字为x,个位数字为y,由题意得:
,
解得:,
原两位数是36,
即:原两位数是36.
故答案是:36.
16.解:设可以购买8元的商品x件,12元的商品y件,
依题意,得:8x+12y=100,
∴x=.
∵x,y均为非负整数,
∴或或或,
∴共有4种购买方案.
故答案为:4.
17.解:把代入方程组,得,解得,
m+n=﹣+=﹣2.
故答案为:﹣2.
18.解:∵直线y=x﹣1与y=﹣x+5的交点坐标是(4,1),
∴方程组的解为.
故答案为:.
19.解:联立得:,
①+②得:8x=8,即x=1,
把x=1代入②得:y=2,
把x=1,y=2代入得:,
解得:a=﹣6,b=﹣2.
20.解:(1)设A,B两种花木的数量分别是x棵、y棵,
,
解得,,
即A,B两种花木的数量分别是4200棵、2400棵;
(2)设安排种植A花木的m人,则种植B花木的(13﹣m)人,
,
解得m=7,
检验:当m=7时,60m≠0,40(13﹣m)≠0,
故原分式方程的解是m=7,
∴13﹣m=6,
答:安排种植A花木的7人,种植B花木的6人,可以确保同时完成各自的任务.
21.解:,
③﹣①得x﹣2y=﹣1④,
由②④组成方程组得,解得,
把代入①得3+2+z=6,
解得z=1,
所以原方程组的解 .
22.解:(1)设直线解析式为y=kx+b,
∵图象过P(﹣1,﹣2),Q(﹣3,4),
∴,
解得,
故一次函数解析式为y=﹣3x﹣5;
(2)∵直线y=kx+b与直线y=﹣2x+3平行,
∴k=﹣2,
∵直线过点(4,6),
∴﹣2×4+b=6,
解得b=14,
故直线解析式为y=﹣2x+14.
23.解:方法一:设房间里有x个椅子,y个凳子,
根据题意得:,
解得:.
答:房间里有12个椅子,4个凳子;
方法二:设房间里有x个椅子,(16﹣x)个凳子,
根据题意得:4x+3(16﹣x)=60,
解得:x=12,
∴16﹣x=4,
答:房间里有12个椅子,4个凳子;
24.方式1:问题:普通公路和高速公路各为多少千米?
解:设普通公路长为x(km),高速公路长为y(km).
根据题意,得,
解得,
答:普通公路长为60km,高速公路长为120km.
方式2:问题:汽车在普通公路和高速公路上各行驶了多少小时?
解:设汽车在普通公路上行驶了x(h),高速公路上行驶了y(h).
根据题意,得,
解得,
答:汽车在普通公路上行驶了1h,高速公路上行驶了1.2h.
方式3:问题:普通公路和两地公路总长各为多少千米?
解:设普通公路长xkm,两地公路总长ykm.
根据题意,得,
解得,
答:普通公路长60km,两地公路总长180km.
方式4:问题:普通公路有多少千米,汽车在普通公路上行驶了多少小时?
解:设普通公路长x(km),汽车在普通公路上行驶了y(h).
根据题意,得,
解得,
答:普通公路长60km,汽车在普通公路上行驶了1h.
25.解:(1)设y与x的关系式为y=kx+b(k≠0),
根据题意得:,
解得:,
∴y与x的关系式为y=5x+400.
(2)当x=1200时,甲公司方案所需费用为5×1200+400=6400(元),
乙公司方案所需费用为5500+(1200﹣1000)×4=6300(元),
∵6400>6300,
∴选择乙公司的服务比较划算.
期末复习提升训练1(附答案)
1.下列四个方程组中,是二元一次方程组的有( )个.
(1),(2)(3)(4).
A.4 B.3 C.2 D.1
2.若是关于x、y的方程组的一个解,则的a+b值为( )
A.0 B.﹣1 C.1 D.﹣2
3.关于x,y的二元一次方程组中,m与方程组的解中的x或y相等,则m的值为( )
A.3或 B.2或﹣ C.3或 D.2或﹣
4.若x2m+ny与x5ym﹣n是同类项,则m,n的值是( )
A.m=2、n=3 B.m=2、n=1 C.m=2、n=0 D.m=1、n=2
5.如果直线y=3x+6与y=2x﹣4交点坐标为(a,b),则是下列哪个方程组的解( )
A. B.
C. D.
6.端午节前夕,某超市用1680元购进A、B两种商品共60件,其中A型商品每件24元,B型商品每件36元.设购买A型商品x件、B型商品y件,依题意列方程组正确的是( )
A. B.
C. D.
7.一个两位数,十位上的数与个位上的数的和是7,若十位上的数与个位上的数对换,得到的两位数与原来的两位数的差是9,则现在的两位数是( )
A.43 B.34 C.25 D.52
8.等腰三角形的周长为15,其中一边长为3,则该等腰三角形的底边长为( )
A.3 B.4 C.5 D.6
9.某商贩在一次买卖中,同时卖出两件上衣,每件都以80元出售,若按成本计算,其中一件盈利60%,另一件亏本20%,在这次买卖中,该商贩( )
A.不盈不亏 B.盈利10元 C.亏损10元 D.盈利50元
10.用若干辆载重量为6千克的货车运一批货物,若每辆汽车只装4千克,则剩下18千克货物;若每辆汽车只装6千克,则最后一辆货车装的货物不足5千克.若设有x辆货车,则x应满足的不等式组是( )
A. B.
C. D.
11.若关于x,y的二元一次方程组的解为则多项式A可以是 (写出一个即可).
12.关于x,y的二元一次方程组,求x= ,y= .
13.如图,已知直线y=ax+b和直线y=kx交于点P,则关于x,y的二元一次方程组的解是 .
14.某市电脑上网每月向用户收取费用y(元)与上网时间x(时)的函数关系如图,当客户每月上网121时,需付费 元.
15.一个两位数,两个数位上的数字一个是另一个的2倍,若把此两位数的两个数字对调,所得新数比原数大27,则此两位数是 .
16.“双11”促销活动中,小芳的妈妈计划用100元在唯品会购买价格分别为8元和12元的两种商品,则可供小芳妈妈选择的购买方案有 种.
17.已知是方程组的解,则m+n= .
18.已知直线y=x﹣1与y=﹣x+5的交点坐标是(4,1),则方程组的解是 .
19.已知方程组与方程组的解相同,求a、b的值.
20.某市火车站北广场将于2021年底投入使用,计划在广场内种植A,B两种花木共6600棵,若A花木数量是B花木数量的2倍少600棵.
(1)A,B两种花木的数量分别是多少棵?
(2)如果园林处安排13人同时种植这两种花木,每人每天能种植A花木60棵或B花木40棵,应分别安排多少人种植A花木和B花木,才能确保同时完成各自的任务?
21.解方程组.
22.根据下列条件,分别确定一次函数的解析式:
(1)图象过P(﹣1,﹣2),Q(﹣3,4);
(2)直线y=kx+b与直线y=﹣2x+3平行,且过点(4,6).
23.请用两种方法解答下面的应用题:
在一个房间里有四条腿的椅子和三条腿的凳子共16个,如果椅子腿和凳子腿数加起来共有60个,有几个椅子和几个凳子?
24.一辆汽车从A地驶往B地,前路段为普通公路,其余路段为高速公路.已知汽车在普通公路上行驶的速度为60km/h,在高速公路上行驶的速度为100km/h,汽车从A地到B地一共行驶了2.2h.
请你根据以上信息,就该汽车行驶的“路程”或“时间”,提出一个用二元一次方程组解决的问题,并写出解答过程.
25.甲、乙两家绿化养护公司各自推出了校园绿化养护服务的收费方案.
甲公司方案:每月的养护费用y(元)与绿化面积x(平方米)的关系如图所示.
乙公司方案:绿化面积不超过1000平方米时,每月收取费用5500元;绿化面积超过1000平方米时,超过的部分每月每平方米加收4元.
(1)求如图所示的y与x的函数表达式;
(2)如果某学校目前的绿化面积是1200平方米.那么选择哪家公司的服务比较划算.
参考答案
1.解:(1)是二元二次方程组;
(2)是二元二次方程组;
(3)是分式,不是二元一次方程组;
(4)是二元一次方程组;
故选:D.
2.解:把代入方程组得:,
①+②得:a+b=﹣1,
故选:B.
3.解:若m=x,方程组变形为,
解得:,此时m=x=2;
若m=y,方程组变形为,
解得:,此时m=y=﹣,
则m的值为2或﹣,
故选:D.
4.解:∵x2m+ny与x5ym﹣n是同类项,
∴,
①+②得:3m=6,即m=2,
把m=2代入②得:n=1,
故选:B.
5.解:∵直线y=3x+6与y=2x﹣4交点坐标为(a,b),
∴解为的方程组是,
即,
故选:A.
6.解:设购买A型商品x件、B型商品y件,依题意列方程组:
.
故选:B.
7.解:设原来的两位数个位上的数是x,十位上的数是y,
根据题意得,10x+y﹣(10y+x)=9,
解得:x=4,y=3,
答案为43,
故选:A.
8.解:若腰长为3,则底边长为:15﹣3﹣3=9,
∵3+3<9,
∴不能组成三角形,舍去;
若底边长为3,则腰长为:=6;
∴该等腰三角形的底边长为:3;
故选:A.
9.解:设盈利60%的衣服的成本为x元,则x×(1+60%)=80,
解得x=50,
设亏损20%的衣服的成本为y元,y×(1﹣20%)=80,
解得y=100元,
∴总成本为100+50=150元,
∴2×80﹣150=10,
∴这次买卖中他是盈利10元.
故选:B.
10.解:设有x辆货车,
每辆汽车只装4千克,则剩下18千克货物,
所以,货物总重为(4x+18)千克,
每辆汽车只装6千克,则最后一辆货车装的货物不足5千克,
根据等量关系,可得到不等式为:
4x+18﹣6(x﹣1)<5和4x+18﹣6(x﹣1)>0.
故选:D.
11.解:∵关于x,y的二元一次方程组的解为,
而1﹣1=0,
∴多项式A可以是答案不唯一,如x﹣y.
故答案为:答案不唯一,如x﹣y.
12.解:,
①+②,得5x=25,解得x=5,
把x=5代入①,得15+4y=15,解得y=0,
所以方程组的解为.
故答案为:5;0.
13.解:∵直线y=ax+b和直线y=kx交点P的坐标为(1,2),
∴关于x,y的二元一次方程组的解为.
故答案为.
14.解:设后段的解析式为y=kx+b,由图象过点(30,60),(100,90)得,解之得,
所以函数解析式为y=,当x=121时y=99,即此时需付费99元.
15.解:设十位数字为x,个位数字为y,由题意得:
,
解得:,
原两位数是36,
即:原两位数是36.
故答案是:36.
16.解:设可以购买8元的商品x件,12元的商品y件,
依题意,得:8x+12y=100,
∴x=.
∵x,y均为非负整数,
∴或或或,
∴共有4种购买方案.
故答案为:4.
17.解:把代入方程组,得,解得,
m+n=﹣+=﹣2.
故答案为:﹣2.
18.解:∵直线y=x﹣1与y=﹣x+5的交点坐标是(4,1),
∴方程组的解为.
故答案为:.
19.解:联立得:,
①+②得:8x=8,即x=1,
把x=1代入②得:y=2,
把x=1,y=2代入得:,
解得:a=﹣6,b=﹣2.
20.解:(1)设A,B两种花木的数量分别是x棵、y棵,
,
解得,,
即A,B两种花木的数量分别是4200棵、2400棵;
(2)设安排种植A花木的m人,则种植B花木的(13﹣m)人,
,
解得m=7,
检验:当m=7时,60m≠0,40(13﹣m)≠0,
故原分式方程的解是m=7,
∴13﹣m=6,
答:安排种植A花木的7人,种植B花木的6人,可以确保同时完成各自的任务.
21.解:,
③﹣①得x﹣2y=﹣1④,
由②④组成方程组得,解得,
把代入①得3+2+z=6,
解得z=1,
所以原方程组的解 .
22.解:(1)设直线解析式为y=kx+b,
∵图象过P(﹣1,﹣2),Q(﹣3,4),
∴,
解得,
故一次函数解析式为y=﹣3x﹣5;
(2)∵直线y=kx+b与直线y=﹣2x+3平行,
∴k=﹣2,
∵直线过点(4,6),
∴﹣2×4+b=6,
解得b=14,
故直线解析式为y=﹣2x+14.
23.解:方法一:设房间里有x个椅子,y个凳子,
根据题意得:,
解得:.
答:房间里有12个椅子,4个凳子;
方法二:设房间里有x个椅子,(16﹣x)个凳子,
根据题意得:4x+3(16﹣x)=60,
解得:x=12,
∴16﹣x=4,
答:房间里有12个椅子,4个凳子;
24.方式1:问题:普通公路和高速公路各为多少千米?
解:设普通公路长为x(km),高速公路长为y(km).
根据题意,得,
解得,
答:普通公路长为60km,高速公路长为120km.
方式2:问题:汽车在普通公路和高速公路上各行驶了多少小时?
解:设汽车在普通公路上行驶了x(h),高速公路上行驶了y(h).
根据题意,得,
解得,
答:汽车在普通公路上行驶了1h,高速公路上行驶了1.2h.
方式3:问题:普通公路和两地公路总长各为多少千米?
解:设普通公路长xkm,两地公路总长ykm.
根据题意,得,
解得,
答:普通公路长60km,两地公路总长180km.
方式4:问题:普通公路有多少千米,汽车在普通公路上行驶了多少小时?
解:设普通公路长x(km),汽车在普通公路上行驶了y(h).
根据题意,得,
解得,
答:普通公路长60km,汽车在普通公路上行驶了1h.
25.解:(1)设y与x的关系式为y=kx+b(k≠0),
根据题意得:,
解得:,
∴y与x的关系式为y=5x+400.
(2)当x=1200时,甲公司方案所需费用为5×1200+400=6400(元),
乙公司方案所需费用为5500+(1200﹣1000)×4=6300(元),
∵6400>6300,
∴选择乙公司的服务比较划算.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
