2021-2022学年人教版(五四制)九年级数学上册期末复习试题(word版含解析)
文档属性
| 名称 | 2021-2022学年人教版(五四制)九年级数学上册期末复习试题(word版含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 320.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-27 00:00:00 | ||
图片预览




文档简介
2021-2022学年人教五四新版九年级上册数学期末复习试题
一.选择题(共10小题,满分30分,每小题3分)
1.已知二次函数y=x2﹣6x+8,当0<x≤m时,﹣1≤y≤8,则m的值是( )
A.3 B.4 C.6 D.7
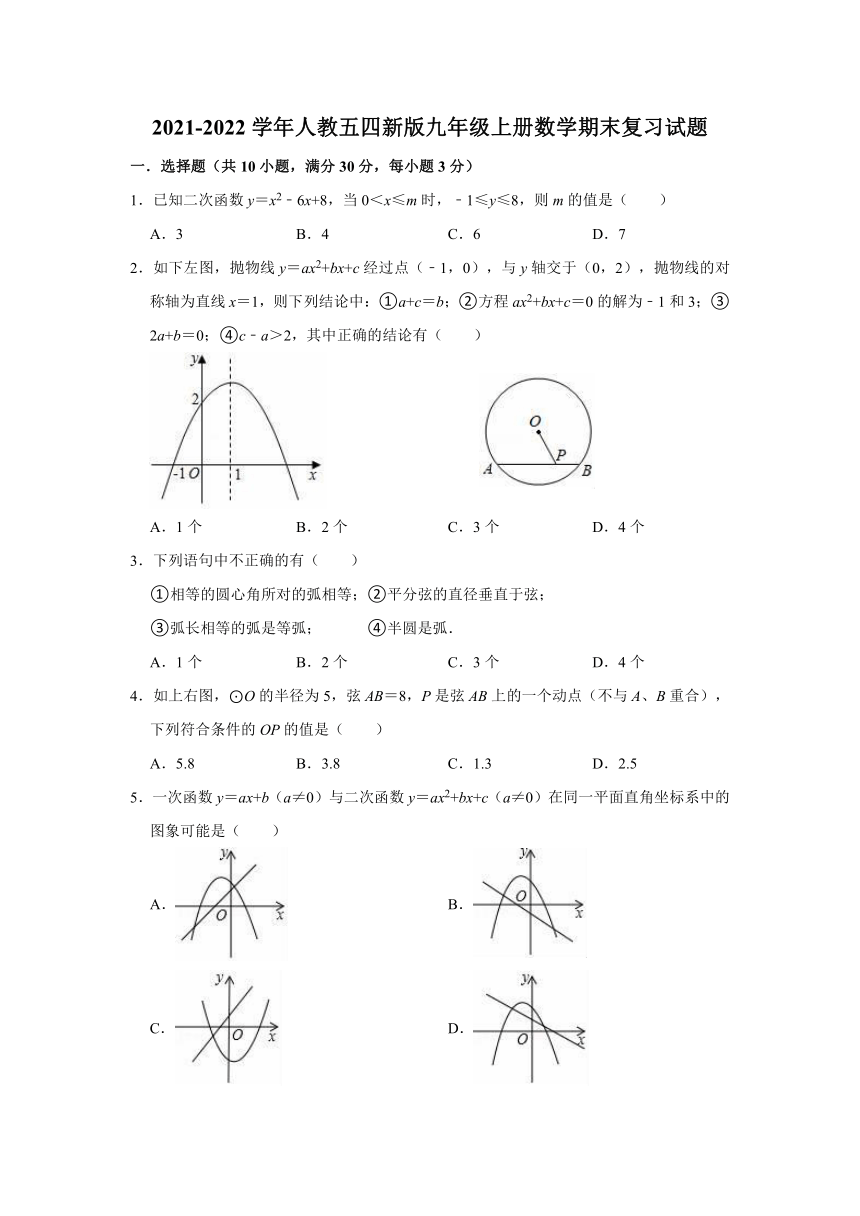
2.如下左图,抛物线y=ax2+bx+c经过点(﹣1,0),与y轴交于(0,2),抛物线的对称轴为直线x=1,则下列结论中:①a+c=b;②方程ax2+bx+c=0的解为﹣1和3;③2a+b=0;④c﹣a>2,其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
3.下列语句中不正确的有( )
①相等的圆心角所对的弧相等;②平分弦的直径垂直于弦;
③弧长相等的弧是等弧; ④半圆是弧.
A.1个 B.2个 C.3个 D.4个
4.如上右图,⊙O的半径为5,弦AB=8,P是弦AB上的一个动点(不与A、B重合),下列符合条件的OP的值是( )
A.5.8 B.3.8 C.1.3 D.2.5
5.一次函数y=ax+b(a≠0)与二次函数y=ax2+bx+c(a≠0)在同一平面直角坐标系中的图象可能是( )
A. B.
C. D.
6.在Rt△ACB中,∠C=90°,,则sinB的值为( )
A. B. C. D.
7.抛物线y=x2﹣4x+4与x轴的公共点的坐标是( )
A.(2,0),(,0) B.(2,0)
C.(0,2) D.(﹣2,0)
8.如下左图,等腰三角形ABC的底边BC长为4,面积是16,腰AC的垂直平分线EF分别交AC,AB边于E,F点.若点D为BC边的中点,点M为线段EF上一动点,则△CDM周长的最小值为( )
A.6 B.8 C.10 D.12
9.如上中图,圆锥的底面半径为6,母线长为10,则圆锥的侧面积是( )
A.36π B.60π C.96π D.100π
10.如上右图,将半径为2cm的圆形纸片翻折,使得、恰好都经过圆心O,折痕为AB、BC,则阴影部分的面积为( )
A.πcm2 B.πcm2 C.πcm2 D.πcm2
二.填空题(共10小题,满分30分,每小题3分)
11.已知y=(m﹣2)x|m|+2是y关于x的二次函数,那么m的值为 .
12.将抛物线y=2x2向左平移2个单位,所得抛物线的对称轴是直线 .
13.如图是二次函数y=ax2+bx+c的部分图象,由图象可知方程ax2+bx+c=0的解是 , .
14.已知⊙O的半径是6cm,点O到同一平面内直线l的距离为5cm,则直线l与⊙O的位置关系是 .
15.如下左图,四边形ABCD是⊙O的外切四边形,且AB=10,CD=15,则四边形ABCD的周长为 .
16.已知二次函数y=ax2+bx+c(a,b,c为整数且a≠0),对一切实数x恒有x≤y≤2x2+,则其解析式为 .
17.在Rt△ABC中,∠C=90°,AC=6,BC=8,则sinA的值为 .
18.用一块等边三角形的硬纸片(如上右图1)做一个底面为等边三角形且高相等的无盖的盒子(边缝忽略不计,如上右图2),在△ABC的每个顶点处各需剪掉一个四边形,其中四边形AMDN中,∠MDN的度数为 .
19.等腰△ABC中,AB=AC=8cm,BC=6cm,则内切圆的半径为 .
20.如下左图,半圆的圆心与坐标原点重合,半圆的半径1,直线l的解析式为y=x+t.若直线l与半圆只有一个交点,则t的取值范围是 .
三.解答题(共8小题,满分60分)
21.(4分)计算:tan60°﹣2cos30°+sin45°.
22.(6分)如上右图,正方形网格中有一段弧,弧上三点A,B,C均在格点上.
(1)直接写出圆心P的坐标,并直接写出cos∠CAP的值.
(2)求的长度.
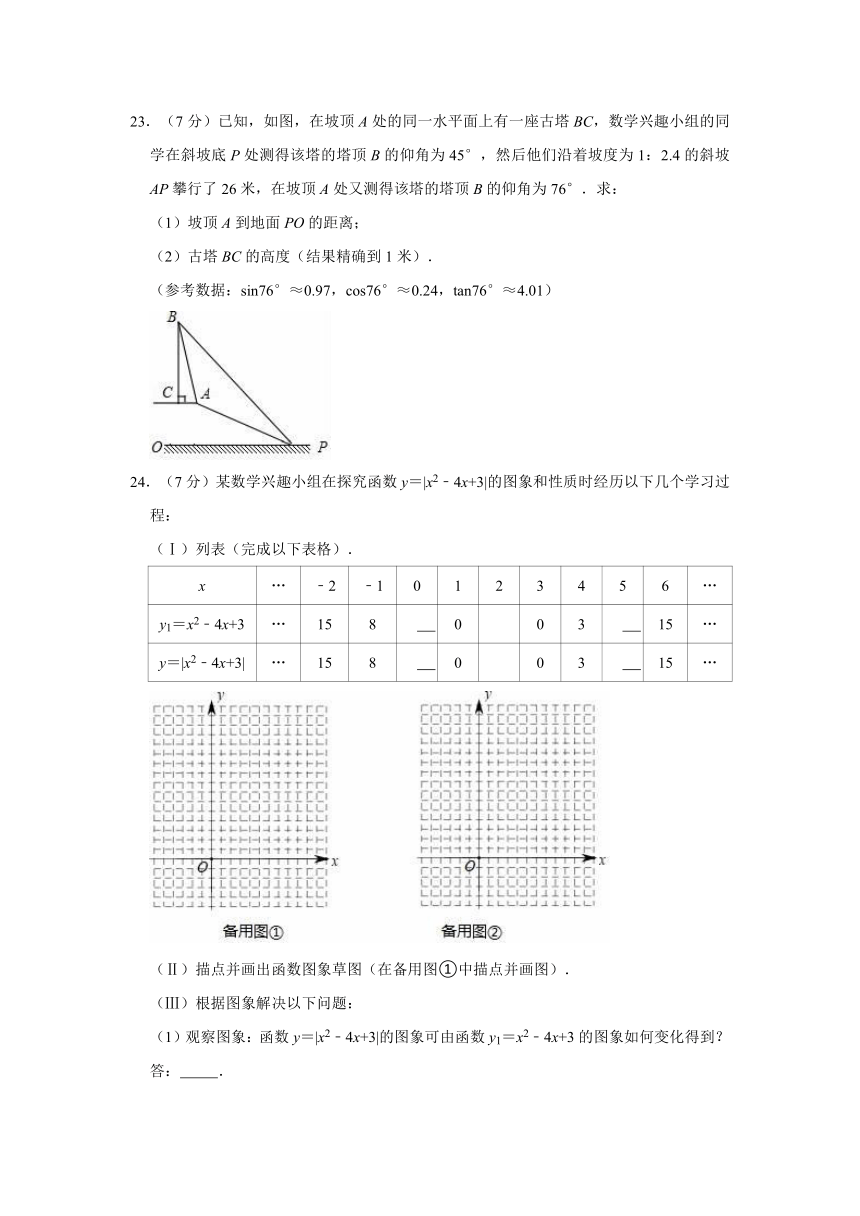
23.(7分)已知,如图,在坡顶A处的同一水平面上有一座古塔BC,数学兴趣小组的同学在斜坡底P处测得该塔的塔顶B的仰角为45°,然后他们沿着坡度为1:2.4的斜坡AP攀行了26米,在坡顶A处又测得该塔的塔顶B的仰角为76°.求:
(1)坡顶A到地面PO的距离;
(2)古塔BC的高度(结果精确到1米).
(参考数据:sin76°≈0.97,cos76°≈0.24,tan76°≈4.01)
24.(7分)某数学兴趣小组在探究函数y=|x2﹣4x+3|的图象和性质时经历以下几个学习过程:
(Ⅰ)列表(完成以下表格).
x … ﹣2 ﹣1 0 1 2 3 4 5 6 …
y1=x2﹣4x+3 … 15 8 0 0 3 15 …
y=|x2﹣4x+3| … 15 8 0 0 3 15 …
(Ⅱ)描点并画出函数图象草图(在备用图①中描点并画图).
(Ⅲ)根据图象解决以下问题:
(1)观察图象:函数y=|x2﹣4x+3|的图象可由函数y1=x2﹣4x+3的图象如何变化得到?
答: .
(2)数学小组探究发现直线y=8与函数y=|x2﹣4x+3|的图象交于点E,F,E(﹣1,8),F(5,8),则不等式|x2﹣4x+3|>8的解集是 .
(3)设函数y=|x2﹣4x+3|的图象与x轴交于A,B两点(B位于A的右侧),与y轴交于点C.
①求直线BC的解析式;
②探究应用:将直线BC沿y轴平移m个单位长度后与函数y=|x2﹣4x+3|的图象恰好有3个交点,求此时m的值.
25.(9分)某游乐场的圆形喷水池中心O有一雕塑OA,从A点向四周喷水,喷出的水柱为抛物线,且形状相同.如图,以水平方向为x轴,点O为原点建立直角坐标系,点A在y轴上,x轴上的点C,D为水柱的落水点,水柱所在抛物线(第一象限部分)的函数表达式为y=﹣(x﹣5)2+6.
(1)求雕塑高OA.
(2)求落水点C,D之间的距离.
(3)若需要在OD上的点E处竖立雕塑EF,OE=10m,EF=1.8m,EF⊥OD.问:顶部F是否会碰到水柱?请通过计算说明.
26.(9分)已知关于x的一元二次方程x2﹣(2k+4)x+k2+4k+3=0.
(1)求证:不论k取何值,此一元二次方程总有两个不相等的实数根;
(2)若此一元二次方程的两根是Rt△ABC两直角边AB、AC的长,斜边BC的长为10,求k的值.
27.(8分)如图,⊙O是△ABC的外接圆,∠ACB=90°.D是⊙O上一点,连接CD,与AB交于点F,过点A作⊙O的切线交DC延长线于点E,已知AC=EC.
(1)求证:AD=AE;
(2)若AE=2,EF=2,求⊙O的直径.
28.(10分)如图,抛物线y=ax2+bx+c经过点C(0,3),与x轴交于点A(﹣1,0)和点B(点B在点A的右边),且OB=OC.
(1)求抛物线的解析式和顶点坐标;
(2)点D、E在直线x=1上的两个动点,且DE=1,点D在点E的上方,求四边形ACDE的周长的最小值.
(3)点P为抛物线上一点,连接CP,直线CP把四边形CBPA的面积分为3:5两部分,求点P的坐标.
参考答案与试题解析
一.选择题(共10小题,满分30分,每小题3分)
1.解:∵二次函数y=x2﹣6x+8=(x﹣3)2﹣1,
∴该函数的对称轴是直线x=3,函数图象开口向上,当x=3时取得最小值﹣1,
∵当0<x≤m时,﹣1≤y≤8,当x=0时,y=8,当x=6时,y=8,
∴m=6,
故选:C.
2.解:①∵抛物线y=ax2+bx+c经过点(﹣1,0),
∴a﹣b+c=0,
∴a+c=b,故本选项正确;
②由对称轴为x=1,一个交点为(﹣1,0),
∴另一个交点为(3,0),
∴方程ax2+bx+c=0的解为﹣1和3,故本选项正确;
③由对称轴为x=1,
∴﹣=1,
∴b=﹣2a,则2a+b=0,故本选项正确;
④∵抛物线y=ax2+bx+c与y轴交于(0,2),
∴c=2,
∵a<0,
∴c﹣a>2,故本选项正确;
故选:D.
3.解:①在同圆或等圆中,相等的圆心角所对的弧相等,故错误;
②平分弦(弦不是直径)的直径垂直于弦,故错误;
③在同圆或等圆中弧长相等的弧是等弧,故错误;
④半圆是弧,故正确;
故选:C.
4.解:过O点作OH⊥AB于H,连接OA,如图,则AH=BH=AB=4,
在Rt△OAH中,OH===3,
所以OP的范围为3≤O<5.
故选:B.
5.解:A、∵二次函数图象开口向下,对称轴在y轴左侧,
∴a<0,b<0,
∴一次函数图象应该过第二、三、四象限,A错误;
B、∵二次函数图象开口向下,对称轴在y轴左侧,
∴a<0,b<0,
∴一次函数图象应该过第二、三、四象限,B正确;
C、∵二次函数图象开口向上,对称轴在y轴右侧,
∴a>0,b<0,
∴一次函数图象应该过第一、三、四象限,C错误;
D、∵二次函数图象开口向下,对称轴在y轴左侧,
∴a<0,b<0,
∴一次函数图象应该过第二、三、四象限,D错误.
故选:B.
6.解:设Rt△ACB中,∠C=90°,∠A、∠B、∠C的对边分别为a、b、c,
由于tanA==2,
可设a=2k,b=k,由勾股定理得,
c==5k,
∴sinB==,
故选:A.
7.解:∵抛物线y=x2﹣4x+4=(x﹣2)2,
∴当y=0时,x=2,
即抛物线y=x2﹣4x+4与x轴的公共点的坐标是(2,0),
故选:B.
8.解:连接AD,
∵△ABC是等腰三角形,点D是BC边的中点,
∴AD⊥BC,
∴S△ABC=BC AD=×4×AD=16,解得AD=8,
∵EF是线段AC的垂直平分线,
∴点C关于直线EF的对称点为点A,
∴AD的长为CM+MD的最小值,
∴△CDM的周长最短=CM+MD+CD=AD+BC=8+×4=8+2=10.
故选:C.
9.解:底面周长是:2×6π=12π,
则圆锥的侧面积是:×12π×10=60π.
故选:B.
10.解:作OD⊥AB于点D,连接AO,BO,CO,如图所示:
∵OD=AO
∴∠OAD=30°,
∴∠AOB=2∠AOD=120°,
同理∠BOC=120°,
∴∠AOC=120°,
∴阴影部分的面积=S扇形BOC=×⊙O面积=×π×22=π(cm2);
故选:C.
二.填空题(共10小题,满分30分,每小题3分)
11.解:∵y=(m﹣2)x|m|+2是y关于x的二次函数,
∴|m|=2,且m﹣2≠0,
解得:m=﹣2.
故答案为:﹣2.
12.解:抛物线y=2x2向左平移2个单位,所得抛物线解析式为:y=2(x+2)2,则其对称轴是直线x=﹣2.
故答案是:x=﹣2.
13.解:由图象可知对称轴x=2,与x轴的一个交点横坐标是5,它到直线x=2的距离是3个单位长度,所以另外一个交点横坐标是﹣1.
所以x1=﹣1,x2=5.
故答案是:x1=﹣1,x2=5.
14.解:设圆的半径为r,点O到直线l的距离为d,
∵d=5,r=6,
∴d<r,
∴直线l与圆相交.
故答案为:相交.
15.解:∵四边形ABCD是⊙O的外切四边形,
∴AE=AH,BE=BF,CF=CG,DH=DG,
∴AD+BC=AB+CD=25,
∴四边形ABCD的周长=AD+BC+AB+CD=25+25=50,
故答案为:50.
16.解:y=ax2+bx+c,对一切实数x恒有x≤y≤2x2+,
∴对一切实数x恒有x≤ax2+bx+c≤2x2+,
∴当x=0时,0≤c≤,
∵c为整数,
∴c=0,
∴x≤ax2+bx≤2x2+,
当ax2+bx≥x时,可得ax2+(b﹣1)x≥0,
∴,
解得b=1,
∴ax2+x≤2x2+,
∴(2﹣a)x2﹣x+≥0,
∴当a=2时,﹣x+≥0不是对于一切x成立,故不符合题意;
当a≠2时,,
解得a≤1,
又∵a>0且为整数,
∴a=1,
∴二次函数的解析式为y=x2+x,
故答案为:y=x2+x.
17.解:∵∠C=90°,AC=6,BC=8,
∴AB==10,
∴sinA===;
故答案为:.
18.解:四边形ANDM角的度数之和为360°,
∵△ABC为等边三角形,
∴∠A=60°,
因为要做一个底面为等边三角形且高相等的无盖的盒子,
所以∠AMD=∠AND=90°,
所以∠MDN=120°.
故填120°.
19.解:如图,设三角形的内切圆为⊙O,切点分别为D、E、F,
过AD⊥BC与D,
设OE=OD=OF=rcm,
∵△ABC是等腰三角形,
∴可以确定A、O、D三点在同一直线上,D是BC的中点,
∴BD=3cm,而AB=8cm,
∴AD==,
根据切线长定理得AE=AF,BD=BE,CD=CF,
∴AE=AF=(AB+AC﹣BC)÷2=5,
∵AB是内切圆的切线,
∴∠AEO=90°=∠ADB,而∠A公共,
∴△ADB∽△AEO,
∴OE:BD=AE:AD
设OE=r,
∴r:3=5:,
∴r=cm.
故答案为: cm.
20.解:若直线与半圆只有一个交点,则有两种情况:直线和半圆相切于点C或从直线过点A开始到直线过点B结束(不包括直线过点A).
直线y=x+t与x轴所形成的锐角是45°.
当直线和半圆相切于点C时,则OC垂直于直线,∠COD=45°.
又OC=1,则CD=OD=,即点C(﹣,),
把点C的坐标代入直线解析式,得
t=y﹣x=,
当直线过点A时,把点A(﹣1,0)代入直线解析式,得t=y﹣x=1.
当直线过点B时,把点B(1,0)代入直线解析式,得t=y﹣x=﹣1.
即当t=或﹣1≤t<1时,直线和圆只有一个公共点;
故答案为t=或﹣1≤t<1.
三.解答题(共8小题,满分60分)
21.解:原式=﹣2×+
=﹣+
=.
22.解:(1)如图所示:圆心P的坐标为:(﹣2,1),
∵AP=PC=,AC=2,
∴AP2+PC2=AC2,
∴△APC是等腰直角三角形,
∴∠CAP=45°,
∴cos∠CAP=;
(2)的长度为:=π.
23.解:(1)过点A作AH⊥PO,垂足为点H,
∵斜坡AP的坡度为1:2.4,
∴=,
设AH=5k,则PH=12k,由勾股定理,得AP=13k,
∴13k=26,
解得k=2,
∴AH=10,
答:坡顶A到地面PO的距离为10米.
(2)延长BC交PO于点D,
∵BC⊥AC,AC∥PO,
∴BD⊥PO,
∴四边形AHDC是矩形,CD=AH=10,AC=DH,
∵∠BPD=45°,
∴PD=BD,
设BC=x,则x+10=24+DH,
∴AC=DH=x﹣14,
在Rt△ABC中,tan76°=,即≈4.01.
解得x≈19.
答:古塔BC的高度约为19米.
24.I解:(Ⅰ)列表(完成表格)
x … ﹣2 ﹣1 0 1 2 3 4 5 6 …
y1=x2﹣4x+3 … 15 8 3 0 ﹣1 0 3 8 15 …
y=|x2﹣4x+3| … 15 8 3 0 1 0 3 8 15 …
(Ⅱ)描点并画图.
(Ⅲ)(1)y=|x2﹣4x+3|的图象可由函数y1=x2﹣4x+3将x轴下方图象关于x轴对称,x轴上方图象不变得到;
故答案为x轴下方图象关于x轴对称,x轴上方图象不变;
(2)结合图象,|x2﹣4x+3|>8时,y=|x2﹣4x+3|图象在y=8的上方,
∴解集是x>5或x<﹣1;
故答案为x>5或x<﹣1
(3)①令x=0,则y=|x2﹣4x+3|=3,
令y=0,则y=|x2﹣4x+3|=0,解得x=1或3,
∴A(1,0),B(3,0),C(0,3),
∴设直线BC的解析式为y=kx+b(k≠0),
则
∴
∴y=﹣x+3;
②直线BC过(0,3),(2,1)和(3,0)三个点,如图所示,
此时,直线BC与y=|x2﹣4x+3|的图象只有3个交点,
∴m=0.
设直线BC向上平移后的直线为y=﹣x+3+m,
∵平移后的直线与函数y=|x2﹣4x+3|的图象恰好有3个交点,
∴直线BC只能向上平移,且直线y=﹣x+3+m和y=﹣x2+4x﹣3有且只有一个交点,
则只有一个解,
于是,消去y得x2﹣5x+6+m=0有两个相等的实数根,
∴△=1﹣4m=0,
∴m=.
综上所述,m=0或m=时将直线BC沿y轴平移m个单位长度后与函数y=|x2﹣4x+3|的图象恰好有3个交点.
25.解:(1)当x=0时,y=﹣×(0﹣5)2+6=,
∴点A的坐标为(0,),
∴雕塑高m.
(2)当y=0时,﹣(x﹣5)2+6=0,
解得:x1=﹣1(舍去),x2=11,
∴点D的坐标为(11,0),
∴OD=11m.
∵从A点向四周喷水,喷出的水柱为抛物线,且形状相同,
∴OC=OD=11m,
∴CD=OC+OD=22m.
(3)当x=10时,y=﹣×(10﹣5)2+6=,
∴点(10,)在抛物线y=﹣(x﹣5)2+6上.
又∵≈1.83>1.8,
∴顶部F不会碰到水柱.
26.(1)证明:∵Δ=[﹣(2k+4)]2﹣4(k2+4k+3)
=4>0,
∴不论k取何值,此一元二次方程总有两个不相等的实数根;
(2)解:x2﹣(2k+4)x+k2+4k+3=0,
(x﹣k﹣1)(x﹣k﹣3)=0,
∴x1=k+1>0,x2=k+3>0,
∴Rt△ABC两直角边的长为k+1和k+3,斜边BC的长为10,
∴(k+1)2+(k+3)2=102,
解得k1=﹣9(舍去),k2=5,
∴k的值为5.
27.(1)证明:∵∠ACB=90°.
∴AB是⊙O的直径,
∵EA是⊙O的切线,
∴BA⊥EA,
∴∠EAC+∠CAB=90°,
∵∠B+∠CAB=90°,
∴∠EAC=∠B,
∵AC=EC,
∴∠EAC=∠E,
∴∠E=∠B,
∵∠B=∠D,
∴∠E=∠D,
∴AD=AE;
(2)解:∵∠EAF=90°,AE=2,EF=2,
∴AF==2,
由(1)知:AD=AE=2,
∵∠B=∠E,∠ACB=∠EAF=90°,
∴△ACB∽△FAE,
∴=,
∴AB=AC,
如图,过点A作AG⊥CD于点G,
设AC=EC=t,则CF=2﹣t,
∵tan∠E==,
sin∠E===,
∴AG=,
∴FG==,
∴EG=EC+CG,
∴CG=CF﹣FG=2﹣t﹣=﹣t,
∵AC2=AG2+CG2,
∴t2=()2+(﹣t)2,
解得t=,
∴AB=AC=t=3.
∴⊙O的直径是3.
28.解:(1)∵点C(0,3),OB=OC,
∴B(3,0),
把A、B、C三点坐标代入y=ax2+bx+c,得
,
解得,,
∴抛物线的解析式为:y=﹣x2+2x+3,
∵y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴顶点坐标为(1,4);
(2)把C向下移1个单位得点C′,再作C′关于抛物线的对称轴的对称点C″,连接AC″,与对称轴交于点E,再在对称轴上E点上方取点D,使得DE=1,连接CD,则CD=C′E=C″E,
∵C(0,3),
∴C′(0,2),
∵对称轴是直线x=1,
∴C″(2,2),
∵A(﹣1,0),
∴AC=,
AC″=,
AE+DE+CD+AC=AE+1+C″E+=1++AE+C″E=1++AC″=1+的值最小,
∴四边形ACDE的周长的最小值为1+;
(3)如图,设直线CP交x轴于点E,
直线CP把四边形CBPA的面积分为3:5两部分,
又∵S△PCB:S△PCA=EB×(yC﹣yP):AE×(yC﹣yP)=BE:AE,
则BE:AE=3:5或5:3,
则AE=2.5或1.5,
即点E的坐标为(1.5,0)或(0.5,0),
将点E的坐标代入直线CP的表达式:y=kx+3,
解得:k=﹣6或﹣2,
故直线CP的表达式为:y=﹣2x+3或y=﹣6x+3,
联立方程组或,
解得:x=4或8(不合题意值已舍去),
故点P的坐标为(4,﹣5)或(8,﹣45)
一.选择题(共10小题,满分30分,每小题3分)
1.已知二次函数y=x2﹣6x+8,当0<x≤m时,﹣1≤y≤8,则m的值是( )
A.3 B.4 C.6 D.7
2.如下左图,抛物线y=ax2+bx+c经过点(﹣1,0),与y轴交于(0,2),抛物线的对称轴为直线x=1,则下列结论中:①a+c=b;②方程ax2+bx+c=0的解为﹣1和3;③2a+b=0;④c﹣a>2,其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
3.下列语句中不正确的有( )
①相等的圆心角所对的弧相等;②平分弦的直径垂直于弦;
③弧长相等的弧是等弧; ④半圆是弧.
A.1个 B.2个 C.3个 D.4个
4.如上右图,⊙O的半径为5,弦AB=8,P是弦AB上的一个动点(不与A、B重合),下列符合条件的OP的值是( )
A.5.8 B.3.8 C.1.3 D.2.5
5.一次函数y=ax+b(a≠0)与二次函数y=ax2+bx+c(a≠0)在同一平面直角坐标系中的图象可能是( )
A. B.
C. D.
6.在Rt△ACB中,∠C=90°,,则sinB的值为( )
A. B. C. D.
7.抛物线y=x2﹣4x+4与x轴的公共点的坐标是( )
A.(2,0),(,0) B.(2,0)
C.(0,2) D.(﹣2,0)
8.如下左图,等腰三角形ABC的底边BC长为4,面积是16,腰AC的垂直平分线EF分别交AC,AB边于E,F点.若点D为BC边的中点,点M为线段EF上一动点,则△CDM周长的最小值为( )
A.6 B.8 C.10 D.12
9.如上中图,圆锥的底面半径为6,母线长为10,则圆锥的侧面积是( )
A.36π B.60π C.96π D.100π
10.如上右图,将半径为2cm的圆形纸片翻折,使得、恰好都经过圆心O,折痕为AB、BC,则阴影部分的面积为( )
A.πcm2 B.πcm2 C.πcm2 D.πcm2
二.填空题(共10小题,满分30分,每小题3分)
11.已知y=(m﹣2)x|m|+2是y关于x的二次函数,那么m的值为 .
12.将抛物线y=2x2向左平移2个单位,所得抛物线的对称轴是直线 .
13.如图是二次函数y=ax2+bx+c的部分图象,由图象可知方程ax2+bx+c=0的解是 , .
14.已知⊙O的半径是6cm,点O到同一平面内直线l的距离为5cm,则直线l与⊙O的位置关系是 .
15.如下左图,四边形ABCD是⊙O的外切四边形,且AB=10,CD=15,则四边形ABCD的周长为 .
16.已知二次函数y=ax2+bx+c(a,b,c为整数且a≠0),对一切实数x恒有x≤y≤2x2+,则其解析式为 .
17.在Rt△ABC中,∠C=90°,AC=6,BC=8,则sinA的值为 .
18.用一块等边三角形的硬纸片(如上右图1)做一个底面为等边三角形且高相等的无盖的盒子(边缝忽略不计,如上右图2),在△ABC的每个顶点处各需剪掉一个四边形,其中四边形AMDN中,∠MDN的度数为 .
19.等腰△ABC中,AB=AC=8cm,BC=6cm,则内切圆的半径为 .
20.如下左图,半圆的圆心与坐标原点重合,半圆的半径1,直线l的解析式为y=x+t.若直线l与半圆只有一个交点,则t的取值范围是 .
三.解答题(共8小题,满分60分)
21.(4分)计算:tan60°﹣2cos30°+sin45°.
22.(6分)如上右图,正方形网格中有一段弧,弧上三点A,B,C均在格点上.
(1)直接写出圆心P的坐标,并直接写出cos∠CAP的值.
(2)求的长度.
23.(7分)已知,如图,在坡顶A处的同一水平面上有一座古塔BC,数学兴趣小组的同学在斜坡底P处测得该塔的塔顶B的仰角为45°,然后他们沿着坡度为1:2.4的斜坡AP攀行了26米,在坡顶A处又测得该塔的塔顶B的仰角为76°.求:
(1)坡顶A到地面PO的距离;
(2)古塔BC的高度(结果精确到1米).
(参考数据:sin76°≈0.97,cos76°≈0.24,tan76°≈4.01)
24.(7分)某数学兴趣小组在探究函数y=|x2﹣4x+3|的图象和性质时经历以下几个学习过程:
(Ⅰ)列表(完成以下表格).
x … ﹣2 ﹣1 0 1 2 3 4 5 6 …
y1=x2﹣4x+3 … 15 8 0 0 3 15 …
y=|x2﹣4x+3| … 15 8 0 0 3 15 …
(Ⅱ)描点并画出函数图象草图(在备用图①中描点并画图).
(Ⅲ)根据图象解决以下问题:
(1)观察图象:函数y=|x2﹣4x+3|的图象可由函数y1=x2﹣4x+3的图象如何变化得到?
答: .
(2)数学小组探究发现直线y=8与函数y=|x2﹣4x+3|的图象交于点E,F,E(﹣1,8),F(5,8),则不等式|x2﹣4x+3|>8的解集是 .
(3)设函数y=|x2﹣4x+3|的图象与x轴交于A,B两点(B位于A的右侧),与y轴交于点C.
①求直线BC的解析式;
②探究应用:将直线BC沿y轴平移m个单位长度后与函数y=|x2﹣4x+3|的图象恰好有3个交点,求此时m的值.
25.(9分)某游乐场的圆形喷水池中心O有一雕塑OA,从A点向四周喷水,喷出的水柱为抛物线,且形状相同.如图,以水平方向为x轴,点O为原点建立直角坐标系,点A在y轴上,x轴上的点C,D为水柱的落水点,水柱所在抛物线(第一象限部分)的函数表达式为y=﹣(x﹣5)2+6.
(1)求雕塑高OA.
(2)求落水点C,D之间的距离.
(3)若需要在OD上的点E处竖立雕塑EF,OE=10m,EF=1.8m,EF⊥OD.问:顶部F是否会碰到水柱?请通过计算说明.
26.(9分)已知关于x的一元二次方程x2﹣(2k+4)x+k2+4k+3=0.
(1)求证:不论k取何值,此一元二次方程总有两个不相等的实数根;
(2)若此一元二次方程的两根是Rt△ABC两直角边AB、AC的长,斜边BC的长为10,求k的值.
27.(8分)如图,⊙O是△ABC的外接圆,∠ACB=90°.D是⊙O上一点,连接CD,与AB交于点F,过点A作⊙O的切线交DC延长线于点E,已知AC=EC.
(1)求证:AD=AE;
(2)若AE=2,EF=2,求⊙O的直径.
28.(10分)如图,抛物线y=ax2+bx+c经过点C(0,3),与x轴交于点A(﹣1,0)和点B(点B在点A的右边),且OB=OC.
(1)求抛物线的解析式和顶点坐标;
(2)点D、E在直线x=1上的两个动点,且DE=1,点D在点E的上方,求四边形ACDE的周长的最小值.
(3)点P为抛物线上一点,连接CP,直线CP把四边形CBPA的面积分为3:5两部分,求点P的坐标.
参考答案与试题解析
一.选择题(共10小题,满分30分,每小题3分)
1.解:∵二次函数y=x2﹣6x+8=(x﹣3)2﹣1,
∴该函数的对称轴是直线x=3,函数图象开口向上,当x=3时取得最小值﹣1,
∵当0<x≤m时,﹣1≤y≤8,当x=0时,y=8,当x=6时,y=8,
∴m=6,
故选:C.
2.解:①∵抛物线y=ax2+bx+c经过点(﹣1,0),
∴a﹣b+c=0,
∴a+c=b,故本选项正确;
②由对称轴为x=1,一个交点为(﹣1,0),
∴另一个交点为(3,0),
∴方程ax2+bx+c=0的解为﹣1和3,故本选项正确;
③由对称轴为x=1,
∴﹣=1,
∴b=﹣2a,则2a+b=0,故本选项正确;
④∵抛物线y=ax2+bx+c与y轴交于(0,2),
∴c=2,
∵a<0,
∴c﹣a>2,故本选项正确;
故选:D.
3.解:①在同圆或等圆中,相等的圆心角所对的弧相等,故错误;
②平分弦(弦不是直径)的直径垂直于弦,故错误;
③在同圆或等圆中弧长相等的弧是等弧,故错误;
④半圆是弧,故正确;
故选:C.
4.解:过O点作OH⊥AB于H,连接OA,如图,则AH=BH=AB=4,
在Rt△OAH中,OH===3,
所以OP的范围为3≤O<5.
故选:B.
5.解:A、∵二次函数图象开口向下,对称轴在y轴左侧,
∴a<0,b<0,
∴一次函数图象应该过第二、三、四象限,A错误;
B、∵二次函数图象开口向下,对称轴在y轴左侧,
∴a<0,b<0,
∴一次函数图象应该过第二、三、四象限,B正确;
C、∵二次函数图象开口向上,对称轴在y轴右侧,
∴a>0,b<0,
∴一次函数图象应该过第一、三、四象限,C错误;
D、∵二次函数图象开口向下,对称轴在y轴左侧,
∴a<0,b<0,
∴一次函数图象应该过第二、三、四象限,D错误.
故选:B.
6.解:设Rt△ACB中,∠C=90°,∠A、∠B、∠C的对边分别为a、b、c,
由于tanA==2,
可设a=2k,b=k,由勾股定理得,
c==5k,
∴sinB==,
故选:A.
7.解:∵抛物线y=x2﹣4x+4=(x﹣2)2,
∴当y=0时,x=2,
即抛物线y=x2﹣4x+4与x轴的公共点的坐标是(2,0),
故选:B.
8.解:连接AD,
∵△ABC是等腰三角形,点D是BC边的中点,
∴AD⊥BC,
∴S△ABC=BC AD=×4×AD=16,解得AD=8,
∵EF是线段AC的垂直平分线,
∴点C关于直线EF的对称点为点A,
∴AD的长为CM+MD的最小值,
∴△CDM的周长最短=CM+MD+CD=AD+BC=8+×4=8+2=10.
故选:C.
9.解:底面周长是:2×6π=12π,
则圆锥的侧面积是:×12π×10=60π.
故选:B.
10.解:作OD⊥AB于点D,连接AO,BO,CO,如图所示:
∵OD=AO
∴∠OAD=30°,
∴∠AOB=2∠AOD=120°,
同理∠BOC=120°,
∴∠AOC=120°,
∴阴影部分的面积=S扇形BOC=×⊙O面积=×π×22=π(cm2);
故选:C.
二.填空题(共10小题,满分30分,每小题3分)
11.解:∵y=(m﹣2)x|m|+2是y关于x的二次函数,
∴|m|=2,且m﹣2≠0,
解得:m=﹣2.
故答案为:﹣2.
12.解:抛物线y=2x2向左平移2个单位,所得抛物线解析式为:y=2(x+2)2,则其对称轴是直线x=﹣2.
故答案是:x=﹣2.
13.解:由图象可知对称轴x=2,与x轴的一个交点横坐标是5,它到直线x=2的距离是3个单位长度,所以另外一个交点横坐标是﹣1.
所以x1=﹣1,x2=5.
故答案是:x1=﹣1,x2=5.
14.解:设圆的半径为r,点O到直线l的距离为d,
∵d=5,r=6,
∴d<r,
∴直线l与圆相交.
故答案为:相交.
15.解:∵四边形ABCD是⊙O的外切四边形,
∴AE=AH,BE=BF,CF=CG,DH=DG,
∴AD+BC=AB+CD=25,
∴四边形ABCD的周长=AD+BC+AB+CD=25+25=50,
故答案为:50.
16.解:y=ax2+bx+c,对一切实数x恒有x≤y≤2x2+,
∴对一切实数x恒有x≤ax2+bx+c≤2x2+,
∴当x=0时,0≤c≤,
∵c为整数,
∴c=0,
∴x≤ax2+bx≤2x2+,
当ax2+bx≥x时,可得ax2+(b﹣1)x≥0,
∴,
解得b=1,
∴ax2+x≤2x2+,
∴(2﹣a)x2﹣x+≥0,
∴当a=2时,﹣x+≥0不是对于一切x成立,故不符合题意;
当a≠2时,,
解得a≤1,
又∵a>0且为整数,
∴a=1,
∴二次函数的解析式为y=x2+x,
故答案为:y=x2+x.
17.解:∵∠C=90°,AC=6,BC=8,
∴AB==10,
∴sinA===;
故答案为:.
18.解:四边形ANDM角的度数之和为360°,
∵△ABC为等边三角形,
∴∠A=60°,
因为要做一个底面为等边三角形且高相等的无盖的盒子,
所以∠AMD=∠AND=90°,
所以∠MDN=120°.
故填120°.
19.解:如图,设三角形的内切圆为⊙O,切点分别为D、E、F,
过AD⊥BC与D,
设OE=OD=OF=rcm,
∵△ABC是等腰三角形,
∴可以确定A、O、D三点在同一直线上,D是BC的中点,
∴BD=3cm,而AB=8cm,
∴AD==,
根据切线长定理得AE=AF,BD=BE,CD=CF,
∴AE=AF=(AB+AC﹣BC)÷2=5,
∵AB是内切圆的切线,
∴∠AEO=90°=∠ADB,而∠A公共,
∴△ADB∽△AEO,
∴OE:BD=AE:AD
设OE=r,
∴r:3=5:,
∴r=cm.
故答案为: cm.
20.解:若直线与半圆只有一个交点,则有两种情况:直线和半圆相切于点C或从直线过点A开始到直线过点B结束(不包括直线过点A).
直线y=x+t与x轴所形成的锐角是45°.
当直线和半圆相切于点C时,则OC垂直于直线,∠COD=45°.
又OC=1,则CD=OD=,即点C(﹣,),
把点C的坐标代入直线解析式,得
t=y﹣x=,
当直线过点A时,把点A(﹣1,0)代入直线解析式,得t=y﹣x=1.
当直线过点B时,把点B(1,0)代入直线解析式,得t=y﹣x=﹣1.
即当t=或﹣1≤t<1时,直线和圆只有一个公共点;
故答案为t=或﹣1≤t<1.
三.解答题(共8小题,满分60分)
21.解:原式=﹣2×+
=﹣+
=.
22.解:(1)如图所示:圆心P的坐标为:(﹣2,1),
∵AP=PC=,AC=2,
∴AP2+PC2=AC2,
∴△APC是等腰直角三角形,
∴∠CAP=45°,
∴cos∠CAP=;
(2)的长度为:=π.
23.解:(1)过点A作AH⊥PO,垂足为点H,
∵斜坡AP的坡度为1:2.4,
∴=,
设AH=5k,则PH=12k,由勾股定理,得AP=13k,
∴13k=26,
解得k=2,
∴AH=10,
答:坡顶A到地面PO的距离为10米.
(2)延长BC交PO于点D,
∵BC⊥AC,AC∥PO,
∴BD⊥PO,
∴四边形AHDC是矩形,CD=AH=10,AC=DH,
∵∠BPD=45°,
∴PD=BD,
设BC=x,则x+10=24+DH,
∴AC=DH=x﹣14,
在Rt△ABC中,tan76°=,即≈4.01.
解得x≈19.
答:古塔BC的高度约为19米.
24.I解:(Ⅰ)列表(完成表格)
x … ﹣2 ﹣1 0 1 2 3 4 5 6 …
y1=x2﹣4x+3 … 15 8 3 0 ﹣1 0 3 8 15 …
y=|x2﹣4x+3| … 15 8 3 0 1 0 3 8 15 …
(Ⅱ)描点并画图.
(Ⅲ)(1)y=|x2﹣4x+3|的图象可由函数y1=x2﹣4x+3将x轴下方图象关于x轴对称,x轴上方图象不变得到;
故答案为x轴下方图象关于x轴对称,x轴上方图象不变;
(2)结合图象,|x2﹣4x+3|>8时,y=|x2﹣4x+3|图象在y=8的上方,
∴解集是x>5或x<﹣1;
故答案为x>5或x<﹣1
(3)①令x=0,则y=|x2﹣4x+3|=3,
令y=0,则y=|x2﹣4x+3|=0,解得x=1或3,
∴A(1,0),B(3,0),C(0,3),
∴设直线BC的解析式为y=kx+b(k≠0),
则
∴
∴y=﹣x+3;
②直线BC过(0,3),(2,1)和(3,0)三个点,如图所示,
此时,直线BC与y=|x2﹣4x+3|的图象只有3个交点,
∴m=0.
设直线BC向上平移后的直线为y=﹣x+3+m,
∵平移后的直线与函数y=|x2﹣4x+3|的图象恰好有3个交点,
∴直线BC只能向上平移,且直线y=﹣x+3+m和y=﹣x2+4x﹣3有且只有一个交点,
则只有一个解,
于是,消去y得x2﹣5x+6+m=0有两个相等的实数根,
∴△=1﹣4m=0,
∴m=.
综上所述,m=0或m=时将直线BC沿y轴平移m个单位长度后与函数y=|x2﹣4x+3|的图象恰好有3个交点.
25.解:(1)当x=0时,y=﹣×(0﹣5)2+6=,
∴点A的坐标为(0,),
∴雕塑高m.
(2)当y=0时,﹣(x﹣5)2+6=0,
解得:x1=﹣1(舍去),x2=11,
∴点D的坐标为(11,0),
∴OD=11m.
∵从A点向四周喷水,喷出的水柱为抛物线,且形状相同,
∴OC=OD=11m,
∴CD=OC+OD=22m.
(3)当x=10时,y=﹣×(10﹣5)2+6=,
∴点(10,)在抛物线y=﹣(x﹣5)2+6上.
又∵≈1.83>1.8,
∴顶部F不会碰到水柱.
26.(1)证明:∵Δ=[﹣(2k+4)]2﹣4(k2+4k+3)
=4>0,
∴不论k取何值,此一元二次方程总有两个不相等的实数根;
(2)解:x2﹣(2k+4)x+k2+4k+3=0,
(x﹣k﹣1)(x﹣k﹣3)=0,
∴x1=k+1>0,x2=k+3>0,
∴Rt△ABC两直角边的长为k+1和k+3,斜边BC的长为10,
∴(k+1)2+(k+3)2=102,
解得k1=﹣9(舍去),k2=5,
∴k的值为5.
27.(1)证明:∵∠ACB=90°.
∴AB是⊙O的直径,
∵EA是⊙O的切线,
∴BA⊥EA,
∴∠EAC+∠CAB=90°,
∵∠B+∠CAB=90°,
∴∠EAC=∠B,
∵AC=EC,
∴∠EAC=∠E,
∴∠E=∠B,
∵∠B=∠D,
∴∠E=∠D,
∴AD=AE;
(2)解:∵∠EAF=90°,AE=2,EF=2,
∴AF==2,
由(1)知:AD=AE=2,
∵∠B=∠E,∠ACB=∠EAF=90°,
∴△ACB∽△FAE,
∴=,
∴AB=AC,
如图,过点A作AG⊥CD于点G,
设AC=EC=t,则CF=2﹣t,
∵tan∠E==,
sin∠E===,
∴AG=,
∴FG==,
∴EG=EC+CG,
∴CG=CF﹣FG=2﹣t﹣=﹣t,
∵AC2=AG2+CG2,
∴t2=()2+(﹣t)2,
解得t=,
∴AB=AC=t=3.
∴⊙O的直径是3.
28.解:(1)∵点C(0,3),OB=OC,
∴B(3,0),
把A、B、C三点坐标代入y=ax2+bx+c,得
,
解得,,
∴抛物线的解析式为:y=﹣x2+2x+3,
∵y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴顶点坐标为(1,4);
(2)把C向下移1个单位得点C′,再作C′关于抛物线的对称轴的对称点C″,连接AC″,与对称轴交于点E,再在对称轴上E点上方取点D,使得DE=1,连接CD,则CD=C′E=C″E,
∵C(0,3),
∴C′(0,2),
∵对称轴是直线x=1,
∴C″(2,2),
∵A(﹣1,0),
∴AC=,
AC″=,
AE+DE+CD+AC=AE+1+C″E+=1++AE+C″E=1++AC″=1+的值最小,
∴四边形ACDE的周长的最小值为1+;
(3)如图,设直线CP交x轴于点E,
直线CP把四边形CBPA的面积分为3:5两部分,
又∵S△PCB:S△PCA=EB×(yC﹣yP):AE×(yC﹣yP)=BE:AE,
则BE:AE=3:5或5:3,
则AE=2.5或1.5,
即点E的坐标为(1.5,0)或(0.5,0),
将点E的坐标代入直线CP的表达式:y=kx+3,
解得:k=﹣6或﹣2,
故直线CP的表达式为:y=﹣2x+3或y=﹣6x+3,
联立方程组或,
解得:x=4或8(不合题意值已舍去),
故点P的坐标为(4,﹣5)或(8,﹣45)
同课章节目录
