华师大版九年级上册24.4.2梯形的中位线
文档属性
| 名称 | 华师大版九年级上册24.4.2梯形的中位线 |  | |
| 格式 | zip | ||
| 文件大小 | 86.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-10-29 13:46:30 | ||
图片预览





文档简介
课件25张PPT。梯形的中位线复习:
1.______叫做三角形的中位线;三角形的中位线有___条.
连结三角形两边中点的线段.
2.三角形的中位线性质是:_______
三角形的中位线平行于第三边,并且等于第三边的一半怎样将一张梯形硬纸片剪成两部分,使分成的两部分能拼成一个三角形?操作:
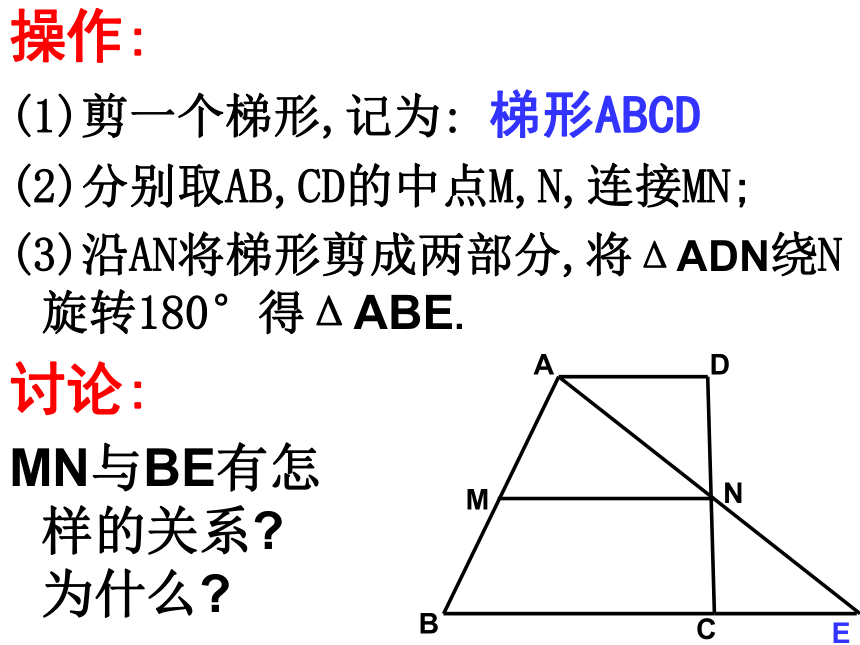
(1)剪一个梯形,记为: 梯形ABCD
(2)分别取AB,CD的中点M,N,连接MN;
(3)沿AN将梯形剪成两部分,将ΔADN绕N旋转180°得ΔABE.
讨论:
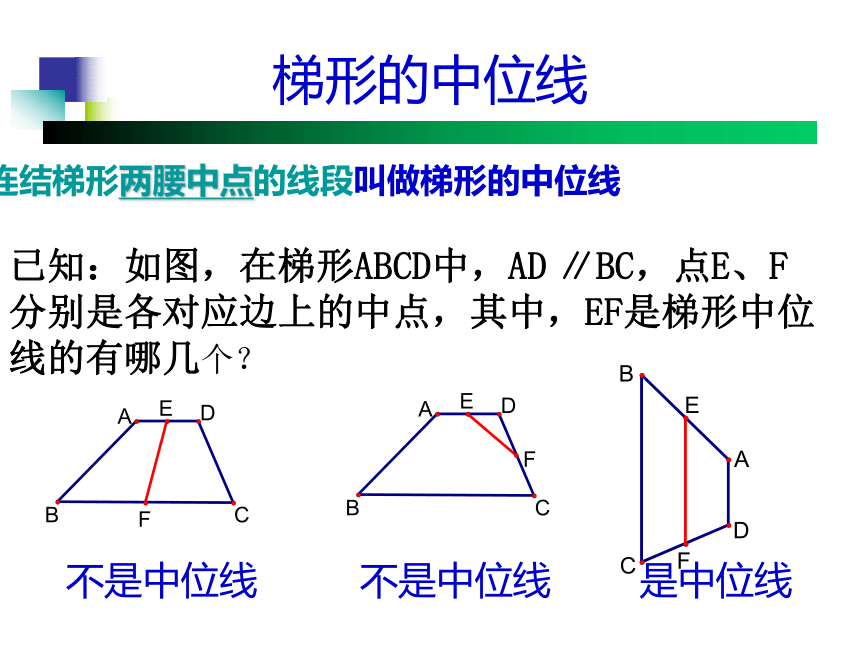
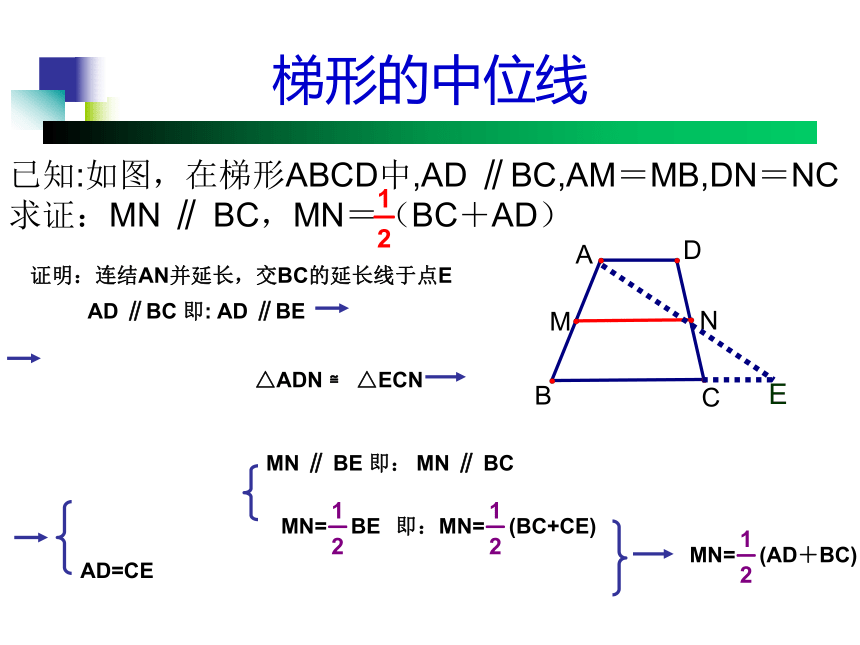
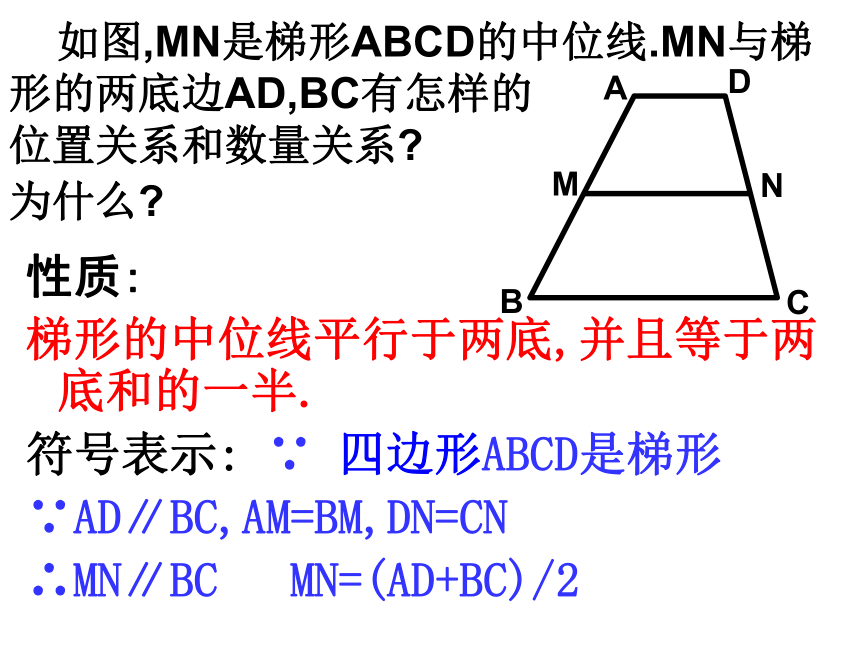
MN与BE有怎 样的关系? 为什么?MN1.梯形中位线的定义: 连结梯形两腰中点的线段叫做梯形的中位线.梯形有__条中位线,而三角形有__条.13梯形的中位线连结梯形两腰中点的线段叫做梯形的中位线已知:如图,在梯形ABCD中,AD ∥BC,点E、F分别是各对应边上的中点,其中,EF是梯形中位线的有哪几个?不是中位线不是中位线是中位线2、梯形中位线定理 梯形的中位线平行于两底,并且等于两底和的一半。问题:怎样证明呢?梯形的中位线MN ∥ BCMN ∥ BE 即:证明:连结AN并延长,交BC的延长线于点E即:MN= (BC+CE)已知:如图,在梯形ABCD中,AD ∥BC,AM=MB,DN=NC求证:MN ∥ BC,MN=(BC+AD) 如图,MN是梯形ABCD的中位线.MN与梯形的两底边AD,BC有怎样的 位置关系和数量关系? 为什么? 性质:
梯形的中位线平行于两底,并且等于两底和的一半.
符号表示: ∵ 四边形ABCD是梯形
∵AD∥BC,AM=BM,DN=CN
∴MN∥BC MN=(AD+BC)/2比较三角形中位线和梯形中位线: 把图中的CD向左平移直至D与点A重合,在这个过程中,上底AD变成一个点,下底BC变成ΔABH的一条边BH,梯形的中位线EF变成的ΔABH中位线EG.ABE3.公式:梯形的面积等于中位线与高之积.细心填一填 1.梯形的上底为6cm,中位线长10cm,则下底为: . 2.已知等腰梯形的中位线为7cm,腰为9cm,则等腰梯形的周长为: . 3.梯形的中位线长为15cm,一条对角线将其分1:2两部分,则梯形的两底分别为 . 4.已知一梯形的中位线为10cm,梯形的高为6cm,则梯形的面积为: . 5.已知一梯形的面积为24cm2,高为6cm,则中位线: . 有一个木匠想制作一个木梯,共需5根横木共200cm,其中最上端的横木长为20cm,求其它四根横木的长度。(每两根横木的距离相等) ??梯形的中位线 有一个木匠想制作一个木梯,共需5根横木共200cm,其中最上端的横木长为20cm,求其它四根横木的长度。(每两根横木的距离相等) ??例2.如图,在等腰梯形ABCD中,AD∥BC,
BC-AD=4cm,GH为梯形的中位线,
GH=6cm,AB=CD=4cm,求该梯形的面积.ABDCEF解:过A、D分别作梯形ABCD的高AE、DF.∴AE=BF,∠AEB=∠DFC=90°在Rt△ABE与Rt△DCF中∴ Rt△ABE≌Rt△DCF (HL)GHEF∴ BE=CF∴ BE=CF= (BC-AD)=2 ∴在Rt△ABE中,
AE= =2∴ 梯形ABCD的面积= GH×AE =6× =12 cm2 GH例3、如图,在直角梯形ABCD中,AD∥BC,∠B=90o,AC将梯形分成两个三角形,其中ΔACD是周长为18cm的等边三角形,求该梯形的中位线长。例4. 如图,梯形ABCD中,M,N分别是对角线BD,AC的中点 求证:MN∥BC,MN=(BC-AD)/2梯形的中位线2、已知:梯形上底为8,中位线为10,
高为6,下底= 面积= 一、填空:12601、如图,在梯形ABCD中,AD ∥ BC中位线EF分别交BD、AC于点M、N,若AD=4cm,BC=8cm,则EF= cm,EM= cm,MN= cm622例5、如图:在梯形ABCD中,AD∥BC,对角线AC⊥BD,
EF为梯形的中位线,∠DBC=30°,求证:EF=AC。BDAEFCOG对角线垂直时通常平移对角线≌∠∥△ 简要分析: 如图,等腰梯形ABCD的两条对角线互相垂直, EF为中位线, DH是梯形的高. 求证:EF=DH.思维拓展分析:过点D作AC的平行线,交BC的延长线于G.小结1.梯形的中位线概念.
2. 梯形中位线定理:
梯形的中位线平行于两底,并且等于两底和的一半 教学反思 梯形的中位线有何性质?梯形中位线与三角形中位线有何区别和联系?
1.______叫做三角形的中位线;三角形的中位线有___条.
连结三角形两边中点的线段.
2.三角形的中位线性质是:_______
三角形的中位线平行于第三边,并且等于第三边的一半怎样将一张梯形硬纸片剪成两部分,使分成的两部分能拼成一个三角形?操作:
(1)剪一个梯形,记为: 梯形ABCD
(2)分别取AB,CD的中点M,N,连接MN;
(3)沿AN将梯形剪成两部分,将ΔADN绕N旋转180°得ΔABE.
讨论:
MN与BE有怎 样的关系? 为什么?MN1.梯形中位线的定义: 连结梯形两腰中点的线段叫做梯形的中位线.梯形有__条中位线,而三角形有__条.13梯形的中位线连结梯形两腰中点的线段叫做梯形的中位线已知:如图,在梯形ABCD中,AD ∥BC,点E、F分别是各对应边上的中点,其中,EF是梯形中位线的有哪几个?不是中位线不是中位线是中位线2、梯形中位线定理 梯形的中位线平行于两底,并且等于两底和的一半。问题:怎样证明呢?梯形的中位线MN ∥ BCMN ∥ BE 即:证明:连结AN并延长,交BC的延长线于点E即:MN= (BC+CE)已知:如图,在梯形ABCD中,AD ∥BC,AM=MB,DN=NC求证:MN ∥ BC,MN=(BC+AD) 如图,MN是梯形ABCD的中位线.MN与梯形的两底边AD,BC有怎样的 位置关系和数量关系? 为什么? 性质:
梯形的中位线平行于两底,并且等于两底和的一半.
符号表示: ∵ 四边形ABCD是梯形
∵AD∥BC,AM=BM,DN=CN
∴MN∥BC MN=(AD+BC)/2比较三角形中位线和梯形中位线: 把图中的CD向左平移直至D与点A重合,在这个过程中,上底AD变成一个点,下底BC变成ΔABH的一条边BH,梯形的中位线EF变成的ΔABH中位线EG.ABE3.公式:梯形的面积等于中位线与高之积.细心填一填 1.梯形的上底为6cm,中位线长10cm,则下底为: . 2.已知等腰梯形的中位线为7cm,腰为9cm,则等腰梯形的周长为: . 3.梯形的中位线长为15cm,一条对角线将其分1:2两部分,则梯形的两底分别为 . 4.已知一梯形的中位线为10cm,梯形的高为6cm,则梯形的面积为: . 5.已知一梯形的面积为24cm2,高为6cm,则中位线: . 有一个木匠想制作一个木梯,共需5根横木共200cm,其中最上端的横木长为20cm,求其它四根横木的长度。(每两根横木的距离相等) ??梯形的中位线 有一个木匠想制作一个木梯,共需5根横木共200cm,其中最上端的横木长为20cm,求其它四根横木的长度。(每两根横木的距离相等) ??例2.如图,在等腰梯形ABCD中,AD∥BC,
BC-AD=4cm,GH为梯形的中位线,
GH=6cm,AB=CD=4cm,求该梯形的面积.ABDCEF解:过A、D分别作梯形ABCD的高AE、DF.∴AE=BF,∠AEB=∠DFC=90°在Rt△ABE与Rt△DCF中∴ Rt△ABE≌Rt△DCF (HL)GHEF∴ BE=CF∴ BE=CF= (BC-AD)=2 ∴在Rt△ABE中,
AE= =2∴ 梯形ABCD的面积= GH×AE =6× =12 cm2 GH例3、如图,在直角梯形ABCD中,AD∥BC,∠B=90o,AC将梯形分成两个三角形,其中ΔACD是周长为18cm的等边三角形,求该梯形的中位线长。例4. 如图,梯形ABCD中,M,N分别是对角线BD,AC的中点 求证:MN∥BC,MN=(BC-AD)/2梯形的中位线2、已知:梯形上底为8,中位线为10,
高为6,下底= 面积= 一、填空:12601、如图,在梯形ABCD中,AD ∥ BC中位线EF分别交BD、AC于点M、N,若AD=4cm,BC=8cm,则EF= cm,EM= cm,MN= cm622例5、如图:在梯形ABCD中,AD∥BC,对角线AC⊥BD,
EF为梯形的中位线,∠DBC=30°,求证:EF=AC。BDAEFCOG对角线垂直时通常平移对角线≌∠∥△ 简要分析: 如图,等腰梯形ABCD的两条对角线互相垂直, EF为中位线, DH是梯形的高. 求证:EF=DH.思维拓展分析:过点D作AC的平行线,交BC的延长线于G.小结1.梯形的中位线概念.
2. 梯形中位线定理:
梯形的中位线平行于两底,并且等于两底和的一半 教学反思 梯形的中位线有何性质?梯形中位线与三角形中位线有何区别和联系?
