人教版数学七年级上册1.2.4绝对值 课件(共16张PPT)
文档属性
| 名称 | 人教版数学七年级上册1.2.4绝对值 课件(共16张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 567.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-27 09:27:28 | ||
图片预览





文档简介
(共16张PPT)
1.2 有理数(第4课时) 1.2.4 绝对值
课件说明
本节课学习绝对值的意义.
学习目标:
了解绝对值的表示方法,理解绝对值的意义,会计算有理数的绝对值.
学习重点:
绝对值的代数意义和几何意义.
问题1:看图回答问题.
两辆汽车从同一处O出发,分别向东、西方向行驶10 km,到达A,B两处,它们的行驶路线相同吗?它们的行驶路程相同吗?
结论:它们的行驶路线不同,行驶路程相同.
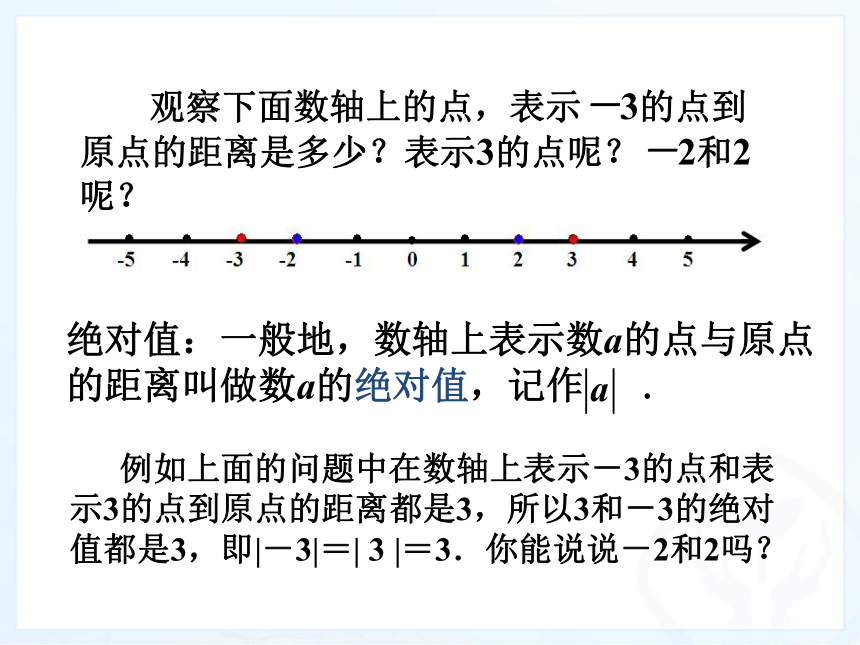
绝对值:一般地,数轴上表示数a的点与原点的距离叫做数a的绝对值,记作 .
观察下面数轴上的点,表示-3的点到原点的距离是多少?表示3的点呢?-2和2呢?
例如上面的问题中在数轴上表示-3的点和表示3的点到原点的距离都是3,所以3和-3的绝对值都是3,即|-3|=| 3 |=3.你能说说-2和2吗?
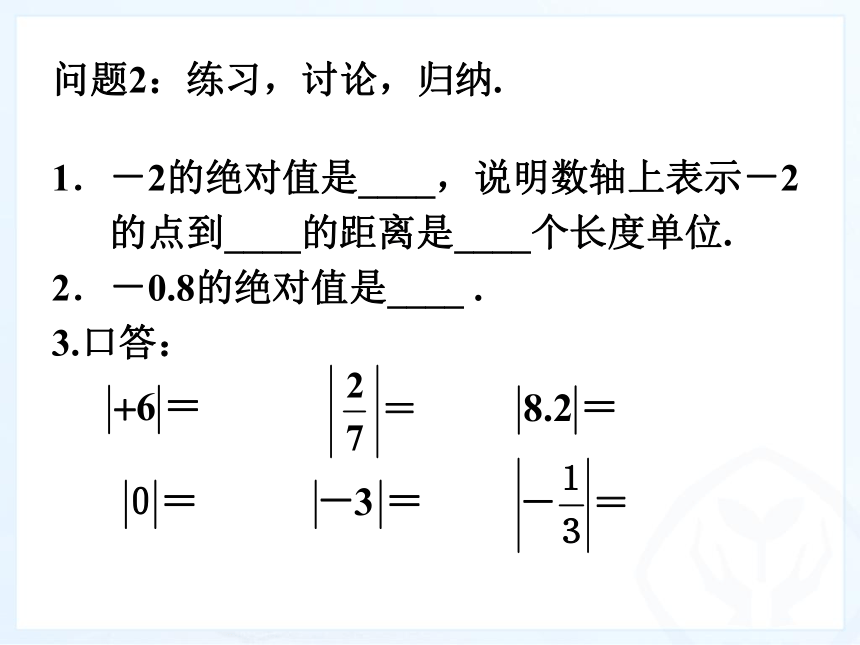
1.-2的绝对值是____,说明数轴上表示-2
的点到____的距离是____个长度单位.
2.-0.8的绝对值是____ .
3.口答:
问题2:练习,讨论,归纳.
教师引导,学生归纳:
(1)一个正数的绝对值是它本身;
(2)一个负数的绝对值是它的相反数;
(3)0的绝对值是0.
问题3:结合上面口答题结果,你能从中发现什么规律?
问题4:小组讨论下面3个问题:
(1)有没有绝对值等于-2的数?
(2)一个数的绝对值会是负数吗?为什么?
(3)不论有理数a取何值,它的绝对值总是什么数?
不论有理数a取何值,它的绝对值总是正数或0(非负数),即对任意有理数a,总有 ≥0
问题5:互为相反数的两个数的绝对值有什么关系?
学生观察讨论:一对相反数虽然分别在原点两边,但它们到原点的距离是相等的.
学生归纳结论:互为相反数的两个数的绝对值相等.
1.题目中涉及到14个不同的气温,你能把这
14个数用数轴上的点表示出来吗?
问题6:请同学们观察教科书第13页思考中的图,回答下面问题.
2.最低气温是多少?最高气温是多少?
3.你觉得两个有理数可以比较大小吗 ?应怎
样比较两个数的大小呢?
数学中规定:在数轴上表示有理数,它们从左到右的顺序,就是从小到大的顺序,即左边的数小于右边的数.
1.正数大于0,0大于负数,正数大于负数;
2.两个负数,绝对值大的反而小.
问题7:对于正数、0和负数这三类数,它们之间有什么大小关系?
请同学们小组讨论,利用数轴探究结论!
练习1. 判断并改错
(1)一个数的绝对值等于本身,则这个数一定是正数;
(2)一个数的绝对值等于它的相反数,则这个数一定
是负数;
(3)如果两个数的绝对值相等,那么这两个数一定相等;
(4)如果两个数不相等,那么这两个数的绝对值一定
不相等;
(5)有理数的绝对值一定是非负数;
(6)两个有理数比大小,绝对值大的反而小.
练习2 拓广探究:
问题8:说说你对绝对值的认识?有理数怎样比较大小?
师生共同归纳:
(1)一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0
(2)若a为有理数,则|a|≥0
(3)零作为一个特殊的数,有它特殊的属性:
绝对值最小的数、相反数是它本身、绝对值是它本身.
(4)有理数比较大小的方法:
方法1.数轴上表示的两个数,右边的总比左边的大;
方法2.正数大于0,0大于负数,正数大于负数;两个负数,绝对值大的反而小 .
教科书习题1.2第5,6,7,8题.
作业:
1.2 有理数(第4课时) 1.2.4 绝对值
课件说明
本节课学习绝对值的意义.
学习目标:
了解绝对值的表示方法,理解绝对值的意义,会计算有理数的绝对值.
学习重点:
绝对值的代数意义和几何意义.
问题1:看图回答问题.
两辆汽车从同一处O出发,分别向东、西方向行驶10 km,到达A,B两处,它们的行驶路线相同吗?它们的行驶路程相同吗?
结论:它们的行驶路线不同,行驶路程相同.
绝对值:一般地,数轴上表示数a的点与原点的距离叫做数a的绝对值,记作 .
观察下面数轴上的点,表示-3的点到原点的距离是多少?表示3的点呢?-2和2呢?
例如上面的问题中在数轴上表示-3的点和表示3的点到原点的距离都是3,所以3和-3的绝对值都是3,即|-3|=| 3 |=3.你能说说-2和2吗?
1.-2的绝对值是____,说明数轴上表示-2
的点到____的距离是____个长度单位.
2.-0.8的绝对值是____ .
3.口答:
问题2:练习,讨论,归纳.
教师引导,学生归纳:
(1)一个正数的绝对值是它本身;
(2)一个负数的绝对值是它的相反数;
(3)0的绝对值是0.
问题3:结合上面口答题结果,你能从中发现什么规律?
问题4:小组讨论下面3个问题:
(1)有没有绝对值等于-2的数?
(2)一个数的绝对值会是负数吗?为什么?
(3)不论有理数a取何值,它的绝对值总是什么数?
不论有理数a取何值,它的绝对值总是正数或0(非负数),即对任意有理数a,总有 ≥0
问题5:互为相反数的两个数的绝对值有什么关系?
学生观察讨论:一对相反数虽然分别在原点两边,但它们到原点的距离是相等的.
学生归纳结论:互为相反数的两个数的绝对值相等.
1.题目中涉及到14个不同的气温,你能把这
14个数用数轴上的点表示出来吗?
问题6:请同学们观察教科书第13页思考中的图,回答下面问题.
2.最低气温是多少?最高气温是多少?
3.你觉得两个有理数可以比较大小吗 ?应怎
样比较两个数的大小呢?
数学中规定:在数轴上表示有理数,它们从左到右的顺序,就是从小到大的顺序,即左边的数小于右边的数.
1.正数大于0,0大于负数,正数大于负数;
2.两个负数,绝对值大的反而小.
问题7:对于正数、0和负数这三类数,它们之间有什么大小关系?
请同学们小组讨论,利用数轴探究结论!
练习1. 判断并改错
(1)一个数的绝对值等于本身,则这个数一定是正数;
(2)一个数的绝对值等于它的相反数,则这个数一定
是负数;
(3)如果两个数的绝对值相等,那么这两个数一定相等;
(4)如果两个数不相等,那么这两个数的绝对值一定
不相等;
(5)有理数的绝对值一定是非负数;
(6)两个有理数比大小,绝对值大的反而小.
练习2 拓广探究:
问题8:说说你对绝对值的认识?有理数怎样比较大小?
师生共同归纳:
(1)一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0
(2)若a为有理数,则|a|≥0
(3)零作为一个特殊的数,有它特殊的属性:
绝对值最小的数、相反数是它本身、绝对值是它本身.
(4)有理数比较大小的方法:
方法1.数轴上表示的两个数,右边的总比左边的大;
方法2.正数大于0,0大于负数,正数大于负数;两个负数,绝对值大的反而小 .
教科书习题1.2第5,6,7,8题.
作业:
