人教版数学六年级下册 3.4 圆柱与圆锥 问题解决 课件(共26张PPT)
文档属性
| 名称 | 人教版数学六年级下册 3.4 圆柱与圆锥 问题解决 课件(共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 9.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-26 04:54:41 | ||
图片预览








文档简介
(共26张PPT)
2022年春人教版数学
六年级下册数学精品课件
问题解决(例7)
人教版 六年级下册
学习目标
使学生在解决问题的过程中体会转化的数学思想。
经历发现问题、 提出问题、分析问题和解决问题的完整过程,掌握问题解决的策略;
能熟练运用圆柱体积计算公式解决实际问题,能用公式计算不规则圆柱的体积或容积;
请你认真阅读,理解一下这道题说的是什么意思?
这个瓶子不是一个完整的圆柱,无法直接计算容积。
一个内直径是8cm的瓶子里,水的高度是7cm,把瓶盖拧紧倒置放平,无水部分是圆柱形,高度是18cm。这个瓶子的容积是多少?
18cm
7cm
能不能转化成圆柱呢?
请你仔细想一想,怎么能计算出瓶子的容积呢?
新课讲解
让我们一起来分析解答这道题吧。
瓶子里水的体积倒置后,体积没变。
水的体积加上18cm高圆柱的体积就是瓶子的容积。
也就是把瓶子的容积转化成两个圆柱的体积。
新课讲解
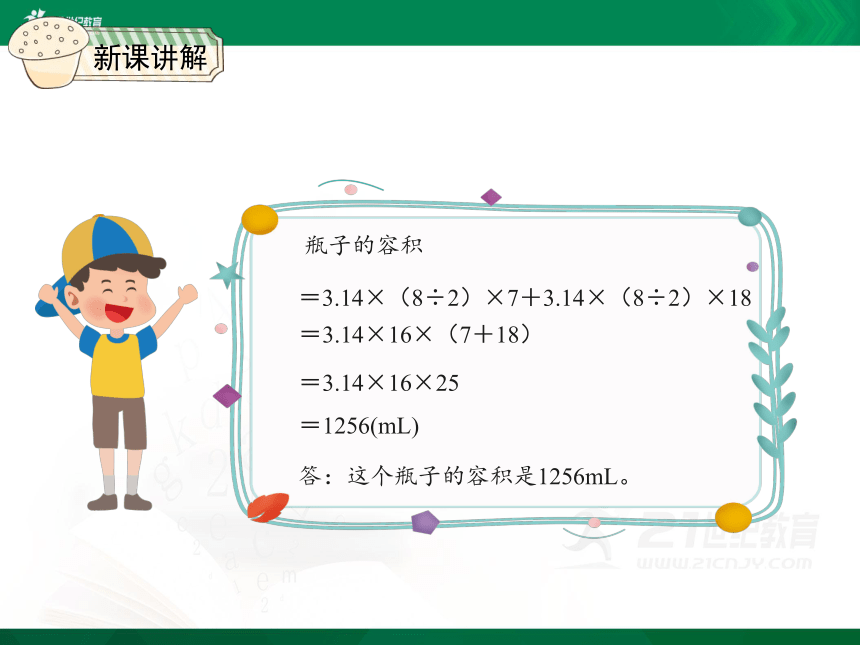
=3.14×(8÷2)×7+3.14×(8÷2)×18
瓶子的容积
=3.14×16×(7+18)
=3.14×16×25
=1256(mL)
答:这个瓶子的容积是1256mL。
新课讲解
让我们回顾反思一下吧!
我们利用了体积不变的特性,把不规则图形转化成规则图形来计算。
在五年级计算梨的体积也是用了转化的方法。
新课讲解
请你仔细想一想,小明喝了的水的体积该怎么计算呢?
无水部分高为10cm圆柱的体积就是小明喝了的水的体积。
一瓶装满的矿泉水,小明喝了一些,把瓶盖拧紧后倒置放平,无水部分高10cm,内径是6cm。小明喝了多少水?
10cm
知识运用
=3.14×9×10
=28.26×10
3.14×(6÷2)×10
2
=282.6(cm )
=282.6(mL)
答:小明喝了282.6mL的水。
知识运用
学校要在教学区和操场之间修一道围墙,原计划用土石35m 。后来多开了一个厚度为25cm的月亮门,减少了土石的用量。现在用了多少立方米的土石?
请你仔细想一想,要想知道现在用多少立方米的土石?就要先求什么?
知识运用
=35-3.14×1×0.25
=35-0.785
35-3.14×(2÷2)×0.25
2
=34.215(m )
答:现在用了34.215立方米的土石。
知识运用
知识运用
两个底面积相等的圆柱,一个高为4.5dm,体积是81dm。另一个高为3dm,它的体积是多少?
通过知道圆柱的高和体积可以求出什么?
=18 ×3
=54(dm )
81 ÷4.5 ×3
答:它的体积是54dm 。
知识运用
一个圆柱形玻璃容器的底面直径是10cm,把一块完全浸泡在这个容器的水中的铁块取出后,水面下降2cm。这块铁块的体积是多少?
请你想一想,如何求这块铁块的体积?
=3.14×5 ×2
=3.14×25×2
=78.5×2
3.14×(10÷2)×2
2
=157(cm )
答:这块铁块的体积是157cm 。
知识运用
右面这个长方形的长是20cm,宽是10cm。 分别以长和宽为轴旋转一周,得到两个圆柱体。它们的体积各是多少?
20cm
10cm
请你想一想,以长为轴旋转,得到的圆柱是什么样子?
=3.14×100×20
=314×20
=6280(cm )
3.14×10 ×20
答:以长为轴旋转一周,得到的圆柱的体积是6280cm 。
知识运用
请你想一想,以宽为轴旋转,得到的圆柱又是什么样子?
=3.14×400×10
=1256×10
=12560(cm )
3.14×20 ×10
答:以宽为轴旋转一周,得到的圆柱的 体积是12560cm 。
知识运用
下面4个图形的面积都是36dm (图中单位:dm)。用这些图形分别卷成圆柱,哪个圆柱的体积最小?哪个圆柱的体积最大?你有什么发现?
图1
图2
图3
图4
18
12
9
6
2
3
4
6
请你想一想,上面4个图形当以长为圆柱底面周长时,会卷成什么样的圆柱?请你动手试一试。
设π=3
图1
半径:18÷3÷2=3(dm)
图2
半径:12÷3÷2=2(dm)
图3
半径:9÷3÷2=1.5(dm)
图4
半径:6÷3÷2=1(dm)
体积:3×3 ×2=54(dm )
体积:3×2 ×3=36(dm )
体积:3×1.5 ×4=27(dm )
体积:3×1 ×6=18(dm )
答:图4圆柱的体积最小,图1圆柱的体积最大。
知识运用
我发现,上面4个图形。当以长作为圆柱底面周长时,长方形的长和宽的长度越接近,所卷成的圆柱的体积越小。
知识运用
下面4个图形的面积都是36dm (图中单位:dm)。用这些图形分别卷成圆柱,哪个圆柱的体积最小?哪个圆柱的体积最大?你有什么发现?
图1
图2
图3
图4
18
12
9
6
2
3
4
6
请你想一想,上面4个图形当以宽为圆柱底面周长时,会卷成什么样的圆柱?请你动手试一试。
图1
半径:2÷3÷2≈0.3(dm)
图2
半径:3÷3÷2=0.5(dm)
图3
半径:4÷3÷2≈0.7(dm)
图4
半径:6÷3÷2=1(dm)
体积:3×0.3 ×18=4.86(dm )
体积:3×0.5 ×12=9(dm )
体积:3×0.7 ×9=13.23(dm )
体积:3×1 ×6=18(dm )
答:图1圆柱的体积最小,图4圆柱的体积最大。
设π=3
知识运用
我发现,上面4个图形。当以宽作为圆柱底面周长时,长方形的长和宽的长度越接近,所卷成的圆柱的体积越大。
课堂游戏
地球被外星人占领,需要小朋友们一起来击败外星人,保卫地球。请你们解决下列的问题,并选择正确答案,选择正确则可发射炸弹击败外星人。小朋友们,保卫地球就靠你们啦!
击败外星人
一个圆柱形粮囤,从里面量得底面半径2m,高3m,如果每立方米玉米重750kg,这个粮囤能装多少吨玉米?
14.13
2826
28260
一个底面半径是20cm、高是30cm的圆柱形鱼缸里装有一些水,向鱼缸里放入一块鹅卵石(完全浸入水中),水面上升了1.5cm。这块鹅卵石的体积是多少立方厘米?
4239
1256
1884
如图,一个饮料瓶内饮料的高度是6cm,将这个饮料瓶的瓶盖拧紧倒置放平,空余部分的高度是10cm。已知这个饮料瓶的容积是672mL,则瓶内的饮料有多少毫升?
42
672
252
课堂小结
在计算不规则图形的体积时,我们可以把不规则图形变成规则图形进行计算。
https://www.21cnjy.com/help/help_extract.php
2022年春人教版数学
六年级下册数学精品课件
问题解决(例7)
人教版 六年级下册
学习目标
使学生在解决问题的过程中体会转化的数学思想。
经历发现问题、 提出问题、分析问题和解决问题的完整过程,掌握问题解决的策略;
能熟练运用圆柱体积计算公式解决实际问题,能用公式计算不规则圆柱的体积或容积;
请你认真阅读,理解一下这道题说的是什么意思?
这个瓶子不是一个完整的圆柱,无法直接计算容积。
一个内直径是8cm的瓶子里,水的高度是7cm,把瓶盖拧紧倒置放平,无水部分是圆柱形,高度是18cm。这个瓶子的容积是多少?
18cm
7cm
能不能转化成圆柱呢?
请你仔细想一想,怎么能计算出瓶子的容积呢?
新课讲解
让我们一起来分析解答这道题吧。
瓶子里水的体积倒置后,体积没变。
水的体积加上18cm高圆柱的体积就是瓶子的容积。
也就是把瓶子的容积转化成两个圆柱的体积。
新课讲解
=3.14×(8÷2)×7+3.14×(8÷2)×18
瓶子的容积
=3.14×16×(7+18)
=3.14×16×25
=1256(mL)
答:这个瓶子的容积是1256mL。
新课讲解
让我们回顾反思一下吧!
我们利用了体积不变的特性,把不规则图形转化成规则图形来计算。
在五年级计算梨的体积也是用了转化的方法。
新课讲解
请你仔细想一想,小明喝了的水的体积该怎么计算呢?
无水部分高为10cm圆柱的体积就是小明喝了的水的体积。
一瓶装满的矿泉水,小明喝了一些,把瓶盖拧紧后倒置放平,无水部分高10cm,内径是6cm。小明喝了多少水?
10cm
知识运用
=3.14×9×10
=28.26×10
3.14×(6÷2)×10
2
=282.6(cm )
=282.6(mL)
答:小明喝了282.6mL的水。
知识运用
学校要在教学区和操场之间修一道围墙,原计划用土石35m 。后来多开了一个厚度为25cm的月亮门,减少了土石的用量。现在用了多少立方米的土石?
请你仔细想一想,要想知道现在用多少立方米的土石?就要先求什么?
知识运用
=35-3.14×1×0.25
=35-0.785
35-3.14×(2÷2)×0.25
2
=34.215(m )
答:现在用了34.215立方米的土石。
知识运用
知识运用
两个底面积相等的圆柱,一个高为4.5dm,体积是81dm。另一个高为3dm,它的体积是多少?
通过知道圆柱的高和体积可以求出什么?
=18 ×3
=54(dm )
81 ÷4.5 ×3
答:它的体积是54dm 。
知识运用
一个圆柱形玻璃容器的底面直径是10cm,把一块完全浸泡在这个容器的水中的铁块取出后,水面下降2cm。这块铁块的体积是多少?
请你想一想,如何求这块铁块的体积?
=3.14×5 ×2
=3.14×25×2
=78.5×2
3.14×(10÷2)×2
2
=157(cm )
答:这块铁块的体积是157cm 。
知识运用
右面这个长方形的长是20cm,宽是10cm。 分别以长和宽为轴旋转一周,得到两个圆柱体。它们的体积各是多少?
20cm
10cm
请你想一想,以长为轴旋转,得到的圆柱是什么样子?
=3.14×100×20
=314×20
=6280(cm )
3.14×10 ×20
答:以长为轴旋转一周,得到的圆柱的体积是6280cm 。
知识运用
请你想一想,以宽为轴旋转,得到的圆柱又是什么样子?
=3.14×400×10
=1256×10
=12560(cm )
3.14×20 ×10
答:以宽为轴旋转一周,得到的圆柱的 体积是12560cm 。
知识运用
下面4个图形的面积都是36dm (图中单位:dm)。用这些图形分别卷成圆柱,哪个圆柱的体积最小?哪个圆柱的体积最大?你有什么发现?
图1
图2
图3
图4
18
12
9
6
2
3
4
6
请你想一想,上面4个图形当以长为圆柱底面周长时,会卷成什么样的圆柱?请你动手试一试。
设π=3
图1
半径:18÷3÷2=3(dm)
图2
半径:12÷3÷2=2(dm)
图3
半径:9÷3÷2=1.5(dm)
图4
半径:6÷3÷2=1(dm)
体积:3×3 ×2=54(dm )
体积:3×2 ×3=36(dm )
体积:3×1.5 ×4=27(dm )
体积:3×1 ×6=18(dm )
答:图4圆柱的体积最小,图1圆柱的体积最大。
知识运用
我发现,上面4个图形。当以长作为圆柱底面周长时,长方形的长和宽的长度越接近,所卷成的圆柱的体积越小。
知识运用
下面4个图形的面积都是36dm (图中单位:dm)。用这些图形分别卷成圆柱,哪个圆柱的体积最小?哪个圆柱的体积最大?你有什么发现?
图1
图2
图3
图4
18
12
9
6
2
3
4
6
请你想一想,上面4个图形当以宽为圆柱底面周长时,会卷成什么样的圆柱?请你动手试一试。
图1
半径:2÷3÷2≈0.3(dm)
图2
半径:3÷3÷2=0.5(dm)
图3
半径:4÷3÷2≈0.7(dm)
图4
半径:6÷3÷2=1(dm)
体积:3×0.3 ×18=4.86(dm )
体积:3×0.5 ×12=9(dm )
体积:3×0.7 ×9=13.23(dm )
体积:3×1 ×6=18(dm )
答:图1圆柱的体积最小,图4圆柱的体积最大。
设π=3
知识运用
我发现,上面4个图形。当以宽作为圆柱底面周长时,长方形的长和宽的长度越接近,所卷成的圆柱的体积越大。
课堂游戏
地球被外星人占领,需要小朋友们一起来击败外星人,保卫地球。请你们解决下列的问题,并选择正确答案,选择正确则可发射炸弹击败外星人。小朋友们,保卫地球就靠你们啦!
击败外星人
一个圆柱形粮囤,从里面量得底面半径2m,高3m,如果每立方米玉米重750kg,这个粮囤能装多少吨玉米?
14.13
2826
28260
一个底面半径是20cm、高是30cm的圆柱形鱼缸里装有一些水,向鱼缸里放入一块鹅卵石(完全浸入水中),水面上升了1.5cm。这块鹅卵石的体积是多少立方厘米?
4239
1256
1884
如图,一个饮料瓶内饮料的高度是6cm,将这个饮料瓶的瓶盖拧紧倒置放平,空余部分的高度是10cm。已知这个饮料瓶的容积是672mL,则瓶内的饮料有多少毫升?
42
672
252
课堂小结
在计算不规则图形的体积时,我们可以把不规则图形变成规则图形进行计算。
https://www.21cnjy.com/help/help_extract.php
