2021-2022学年人教版数学七年级下册5.1.1相交线课件(共17张PPT)
文档属性
| 名称 | 2021-2022学年人教版数学七年级下册5.1.1相交线课件(共17张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 849.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-27 00:00:00 | ||
图片预览





文档简介
(共17张PPT)
5.1.1 相交线
学习目标
1.通过画两条相交线观察,归纳并掌握邻补角和对顶角的概念,培养学生的观察、识图能力,使学生养成良好的学习习惯
2.通过度量各角推导对顶角性质并用理论说明,理解并会用这个性质进行简单的计算,培养学生形成合作、主动参与的意识
复习
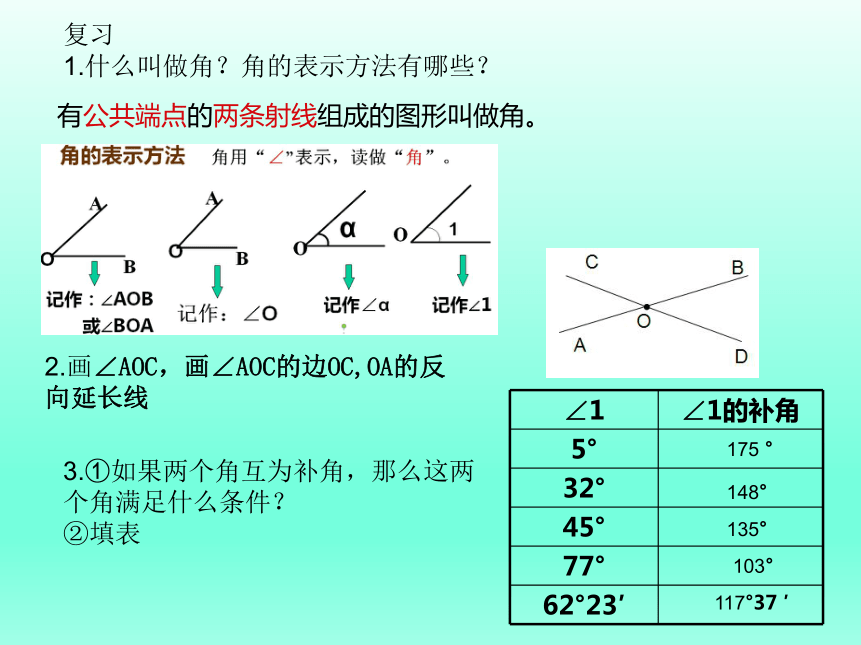
1.什么叫做角?角的表示方法有哪些?
∠1 ∠1的补角
5°
32°
45°
77°
62°23′
3.①如果两个角互为补角,那么这两个角满足什么条件?
②填表
有公共端点的两条射线组成的图形叫做角。
2.画∠AOC,画∠AOC的边OC,OA的反向延长线
175 °
148°
135°
103°
117°37 ′
任务一(主问题)探究:1.任意画两条相交的直线
形成四个角,∠1和∠2有什么特点?∠1和∠3呢?
归纳,什么是邻补角和对顶角
2.图中还有几对∠1和∠2位置关系的角?∠1和∠3呢?
3.分别量各角度数,∠1和∠2的度数有什么关系?∠1和∠3呢?再用理论说明?归纳对顶角的性质,试写出几何语言
4.图中具有这样等量关系的角有几对?
5.剪刀把手之间的角变化的过程中,这个关系还保持吗?为什么?
探究并归纳邻补角和对顶角的概念及推导对顶角性质
C
B
A
D
1
2
3
4
学法指导:
1.自学:仔细阅读探究要求,思考操作程序。
2.互学:组长主持第一环节:有序交流,自由表达,
组长主持第二环节:归纳小结,汇总意见.(通过探
究活动归纳)
3.展学:(1)1号汇报,2号补充,3号总结提升;并板书结论。
(2)声音洪亮,语言流畅,其他同学积极补充,质疑。
(10分钟后展示)
学程一
C
B
A
D
1
2
3
4
∠1+∠2=180 ∠1+∠4=180
∠3+∠2=180 ∠3+∠4=180
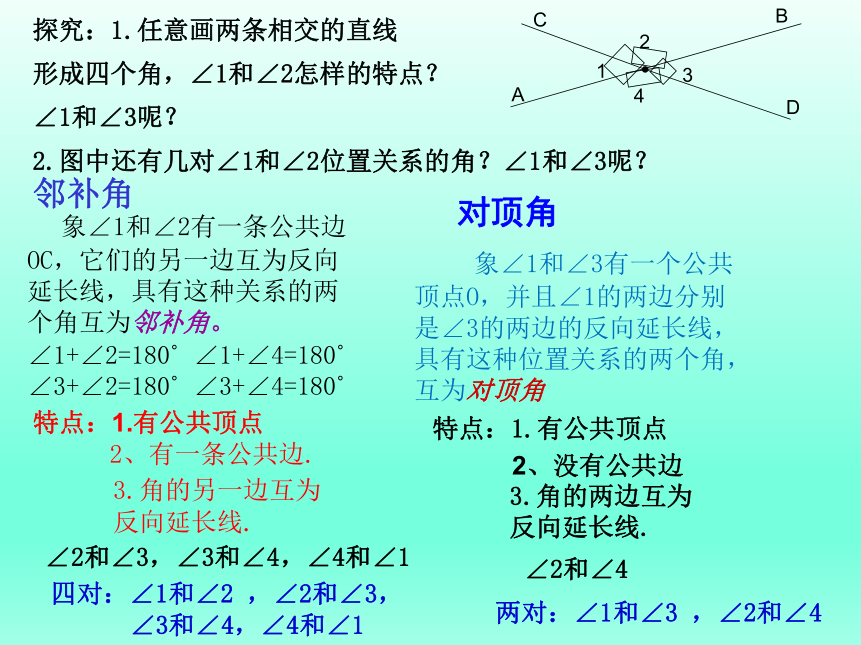
邻补角
象∠1和∠2有一条公共边
OC,它们的另一边互为反向
延长线,具有这种关系的两
个角互为邻补角。
特点:1.有公共顶点
2、有一条公共边.
3.角的另一边互为
反向延长线.
对顶角
象∠1和∠3有一个公共
顶点O,并且∠1的两边分别
是∠3的两边的反向延长线,
具有这种位置关系的两个角,
互为对顶角
特点:1.有公共顶点
2、没有公共边
3.角的两边互为
反向延长线.
探究:1.任意画两条相交的直线
形成四个角,∠1和∠2怎样的特点?
∠1和∠3呢?
2.图中还有几对∠1和∠2位置关系的角?∠1和∠3呢?
∠2和∠3,∠3和∠4,∠4和∠1
∠2和∠4
四对:∠1和∠2 ,∠2和∠3,
∠3和∠4,∠4和∠1
两对:∠1和∠3 ,∠2和∠4
∠2与∠3互补
∵∠1与∠2互补,
∴∠ 2 +∠1= 180°
,
∴∠1= ∠3.
(同角的补角相等)
∠ 2 +∠3=180°,
A
D
对顶角的性质:
对顶角相等
注意:如果∠α和∠β是对顶角,那么一定有∠α=∠β;
反之,如果有∠α=∠β,那么∠α与∠β一定是对顶角吗?
说明 ∵因为 ∴所以
(邻补角定义)
(不一定)
∠1= ∠3,∠2=∠4
3.分别量各角度数,∠1和∠2的度数有什么关系?∠1和∠3呢?再用理论说明?归纳对顶角的性质,试写出几何语言
4.图中具有这样等量关系的角有几对?
5.剪刀把手之间的角变化的过程中,这个关系还保持吗?为什么?
4.两对:∠1= ∠3,∠2=∠4
C
B
A
D
1
2
3
4
5.剪刀把手之间的角变化的过程中,这个关系保持不变
任务二
巩固邻补角和对顶角的概念
1、如图所示,∠1与∠2互为邻补角的是﹙ ﹚
2.下图中,∠1和∠2是对顶角的是﹙ ﹚
3.图所示,∠1和∠2是对顶角的是( )
D
B
C
学法指导:
1.自学:学生独立完成3道题;
2.展学:个体展示。 (2分钟后展示)
学程一
对顶角性质的应用
学法指导: 1.自学:仔细阅读题目,思考问题,理清解题思路。
2.互学:组长主持第一环节:有序交流,自由表达
组长主持第二环节:归纳小结,汇总意见.
3.展学:声音洪亮,语言流畅,其他同学积极补充,质疑。
(8分钟后展示)
1 如图,直线a、b相交,∠1=40°,求 ∠2、
∠3、∠4的度数.
2
)
1
)
(
3
4
(
1
1
)
a
b
(
3
4
(
变式1:若∠1+∠3 = 50°,则∠3= ,
∠2= .
变式2:若∠2是∠1的3倍,则∠3= .
2.已知:如图, ∠ 1=70°,OE平分 ∠ AOC,
求 ∠ EOC 和 ∠ BOC的度数.
1
A
B
C
D
E
O
学程二
1 如图,直线a、b相交,∠1=40°,求
∠2、∠3、∠4的度数.
解:由邻补角的定义可知
∠2=180°-∠1
=180°-40°=140°.
由对顶角相等可得
∠3=∠1=40°,∠4=∠2=140°.
2
)
1
)
(
3
4
(
1
1
)
a
b
(
3
4
(
解:设∠1=x°,则∠2=3x°.
变式2:若∠2是∠1的3倍,求∠3的度数.
根据邻补角的定义,得 x°+3x°=180°.
所以 x=45,
根据对顶角相等,可得
∠3=∠1=45°.
则∠1=45°.
变式1:若∠1+∠3 = 50°,则∠3= ,
∠2= .
25°
155°
a
b
)
(
1
3
4
2
)
(
1.平面上两条直线相交,有几对
对顶角?几对邻补角?
3.平面上n条直线交于一点,有几对对顶角?
有几对邻补角?
2.平面上三条直线交于一点,有几
对对顶角?有几对邻补角?
a
b
c
a
b
a
b
a
c
b
c
2对对顶角,4对邻补角
6对对顶角,12对邻补角
对顶角:n(n-1)
邻补角:2n(n-1)
1.下列各图中∠1、∠2是对顶角的是( )
2.下列各图中∠1、∠2是邻补角的是( )
3.已知互为邻补角的两个角的度数之比为3:2,求这两个角的度数。
4.如图所示,直线AB,CD相交于点O,∠AOC=34 ,∠DOE=56 ,求∠BOD,∠BOC,∠AOE的度数;
当堂检测
学法指导:
1.自学:学生独立完成5道题;
2.互学:校对答案,小组纠错 ;
3.展学:个体展示。 (6分钟后展示)
学程三
E
A
B
C
D
O
1.已知:如图, ∠ 1=70°,OE平分
∠ AOC,求 ∠ EOC和 ∠ BOC的度数.
1
A
B
C
D
E
O
2.如图,三条直线AB、CD、EF相交于点O,求∠1+∠3+∠5等于多少度?
角的名称 特征 性质 相同点 不同点
对
顶
角
邻
补
角
①两条直相交而成的角
②有一个公共顶点
③没有公共边
①两条直相交而成的角
②有一个公共顶点
③有一条公共边
对顶
角相
等
邻补
角互
补
都是两条
直线相交
而成的角,
都有一个
公共顶点,
他们都成
对出现
对顶角没有公
共边而邻补角
有一条公共边;
两条直线相交
时,一个角的
对顶有一个,
而一个角的邻
补角有两个
课堂小结
谈谈本节课你有什么收获?
作 业
小卷(必做、选做)
5.1.1 相交线
学习目标
1.通过画两条相交线观察,归纳并掌握邻补角和对顶角的概念,培养学生的观察、识图能力,使学生养成良好的学习习惯
2.通过度量各角推导对顶角性质并用理论说明,理解并会用这个性质进行简单的计算,培养学生形成合作、主动参与的意识
复习
1.什么叫做角?角的表示方法有哪些?
∠1 ∠1的补角
5°
32°
45°
77°
62°23′
3.①如果两个角互为补角,那么这两个角满足什么条件?
②填表
有公共端点的两条射线组成的图形叫做角。
2.画∠AOC,画∠AOC的边OC,OA的反向延长线
175 °
148°
135°
103°
117°37 ′
任务一(主问题)探究:1.任意画两条相交的直线
形成四个角,∠1和∠2有什么特点?∠1和∠3呢?
归纳,什么是邻补角和对顶角
2.图中还有几对∠1和∠2位置关系的角?∠1和∠3呢?
3.分别量各角度数,∠1和∠2的度数有什么关系?∠1和∠3呢?再用理论说明?归纳对顶角的性质,试写出几何语言
4.图中具有这样等量关系的角有几对?
5.剪刀把手之间的角变化的过程中,这个关系还保持吗?为什么?
探究并归纳邻补角和对顶角的概念及推导对顶角性质
C
B
A
D
1
2
3
4
学法指导:
1.自学:仔细阅读探究要求,思考操作程序。
2.互学:组长主持第一环节:有序交流,自由表达,
组长主持第二环节:归纳小结,汇总意见.(通过探
究活动归纳)
3.展学:(1)1号汇报,2号补充,3号总结提升;并板书结论。
(2)声音洪亮,语言流畅,其他同学积极补充,质疑。
(10分钟后展示)
学程一
C
B
A
D
1
2
3
4
∠1+∠2=180 ∠1+∠4=180
∠3+∠2=180 ∠3+∠4=180
邻补角
象∠1和∠2有一条公共边
OC,它们的另一边互为反向
延长线,具有这种关系的两
个角互为邻补角。
特点:1.有公共顶点
2、有一条公共边.
3.角的另一边互为
反向延长线.
对顶角
象∠1和∠3有一个公共
顶点O,并且∠1的两边分别
是∠3的两边的反向延长线,
具有这种位置关系的两个角,
互为对顶角
特点:1.有公共顶点
2、没有公共边
3.角的两边互为
反向延长线.
探究:1.任意画两条相交的直线
形成四个角,∠1和∠2怎样的特点?
∠1和∠3呢?
2.图中还有几对∠1和∠2位置关系的角?∠1和∠3呢?
∠2和∠3,∠3和∠4,∠4和∠1
∠2和∠4
四对:∠1和∠2 ,∠2和∠3,
∠3和∠4,∠4和∠1
两对:∠1和∠3 ,∠2和∠4
∠2与∠3互补
∵∠1与∠2互补,
∴∠ 2 +∠1= 180°
,
∴∠1= ∠3.
(同角的补角相等)
∠ 2 +∠3=180°,
A
D
对顶角的性质:
对顶角相等
注意:如果∠α和∠β是对顶角,那么一定有∠α=∠β;
反之,如果有∠α=∠β,那么∠α与∠β一定是对顶角吗?
说明 ∵因为 ∴所以
(邻补角定义)
(不一定)
∠1= ∠3,∠2=∠4
3.分别量各角度数,∠1和∠2的度数有什么关系?∠1和∠3呢?再用理论说明?归纳对顶角的性质,试写出几何语言
4.图中具有这样等量关系的角有几对?
5.剪刀把手之间的角变化的过程中,这个关系还保持吗?为什么?
4.两对:∠1= ∠3,∠2=∠4
C
B
A
D
1
2
3
4
5.剪刀把手之间的角变化的过程中,这个关系保持不变
任务二
巩固邻补角和对顶角的概念
1、如图所示,∠1与∠2互为邻补角的是﹙ ﹚
2.下图中,∠1和∠2是对顶角的是﹙ ﹚
3.图所示,∠1和∠2是对顶角的是( )
D
B
C
学法指导:
1.自学:学生独立完成3道题;
2.展学:个体展示。 (2分钟后展示)
学程一
对顶角性质的应用
学法指导: 1.自学:仔细阅读题目,思考问题,理清解题思路。
2.互学:组长主持第一环节:有序交流,自由表达
组长主持第二环节:归纳小结,汇总意见.
3.展学:声音洪亮,语言流畅,其他同学积极补充,质疑。
(8分钟后展示)
1 如图,直线a、b相交,∠1=40°,求 ∠2、
∠3、∠4的度数.
2
)
1
)
(
3
4
(
1
1
)
a
b
(
3
4
(
变式1:若∠1+∠3 = 50°,则∠3= ,
∠2= .
变式2:若∠2是∠1的3倍,则∠3= .
2.已知:如图, ∠ 1=70°,OE平分 ∠ AOC,
求 ∠ EOC 和 ∠ BOC的度数.
1
A
B
C
D
E
O
学程二
1 如图,直线a、b相交,∠1=40°,求
∠2、∠3、∠4的度数.
解:由邻补角的定义可知
∠2=180°-∠1
=180°-40°=140°.
由对顶角相等可得
∠3=∠1=40°,∠4=∠2=140°.
2
)
1
)
(
3
4
(
1
1
)
a
b
(
3
4
(
解:设∠1=x°,则∠2=3x°.
变式2:若∠2是∠1的3倍,求∠3的度数.
根据邻补角的定义,得 x°+3x°=180°.
所以 x=45,
根据对顶角相等,可得
∠3=∠1=45°.
则∠1=45°.
变式1:若∠1+∠3 = 50°,则∠3= ,
∠2= .
25°
155°
a
b
)
(
1
3
4
2
)
(
1.平面上两条直线相交,有几对
对顶角?几对邻补角?
3.平面上n条直线交于一点,有几对对顶角?
有几对邻补角?
2.平面上三条直线交于一点,有几
对对顶角?有几对邻补角?
a
b
c
a
b
a
b
a
c
b
c
2对对顶角,4对邻补角
6对对顶角,12对邻补角
对顶角:n(n-1)
邻补角:2n(n-1)
1.下列各图中∠1、∠2是对顶角的是( )
2.下列各图中∠1、∠2是邻补角的是( )
3.已知互为邻补角的两个角的度数之比为3:2,求这两个角的度数。
4.如图所示,直线AB,CD相交于点O,∠AOC=34 ,∠DOE=56 ,求∠BOD,∠BOC,∠AOE的度数;
当堂检测
学法指导:
1.自学:学生独立完成5道题;
2.互学:校对答案,小组纠错 ;
3.展学:个体展示。 (6分钟后展示)
学程三
E
A
B
C
D
O
1.已知:如图, ∠ 1=70°,OE平分
∠ AOC,求 ∠ EOC和 ∠ BOC的度数.
1
A
B
C
D
E
O
2.如图,三条直线AB、CD、EF相交于点O,求∠1+∠3+∠5等于多少度?
角的名称 特征 性质 相同点 不同点
对
顶
角
邻
补
角
①两条直相交而成的角
②有一个公共顶点
③没有公共边
①两条直相交而成的角
②有一个公共顶点
③有一条公共边
对顶
角相
等
邻补
角互
补
都是两条
直线相交
而成的角,
都有一个
公共顶点,
他们都成
对出现
对顶角没有公
共边而邻补角
有一条公共边;
两条直线相交
时,一个角的
对顶有一个,
而一个角的邻
补角有两个
课堂小结
谈谈本节课你有什么收获?
作 业
小卷(必做、选做)
