沪科版数学八年级上册 15.4 角的平分线 课件(共15张PPT)
文档属性
| 名称 | 沪科版数学八年级上册 15.4 角的平分线 课件(共15张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 132.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-27 10:16:17 | ||
图片预览






文档简介
(共15张PPT)
角的平分线
一条射线
把一个角
分成两个相等的角,
这条射线叫做这个角的平分线。
o
B
C
A
1
2
在半透明的纸上画∠BAC,对折,使角的两条边完全重合,然后用直尺画出折痕OD。
从上面试验可以看出,角是轴对称图形,对称轴是它的角平分线所在的直线。
B
C
A
D
不利用作图工具,请你将一张用纸片做的角分成两个相等的角。你有什么办法?
情景引入
如果前面活动中的纸片换成木板、钢板等没法折的角,又该怎么办呢?
用尺规作图的方法作出角的平分线。
探究
已知:如图,∠AOB。求作:∠AOB的平分线。
O
A
B
C
M
N
画法:
1.以O为圆心,适当长为半径作弧,交OA于M,交OB于N。
2.分别以M、N为圆心。大于1/2MN的长为半径作弧。两弧在∠AOB的内部交于C。
3.作射线OC。
射线OC即为所求。
B
A
.
C
E
D
过直线上一点作这条直线的垂线
画法:
1.以C为圆心,适当长为半径作弧,交AB于D,E。
2.分别以D,E为圆心。大于 1/2 DE的长为半径作弧。两弧交于F。
3.作直线FC,直线FC,即为所求。
F
A
D
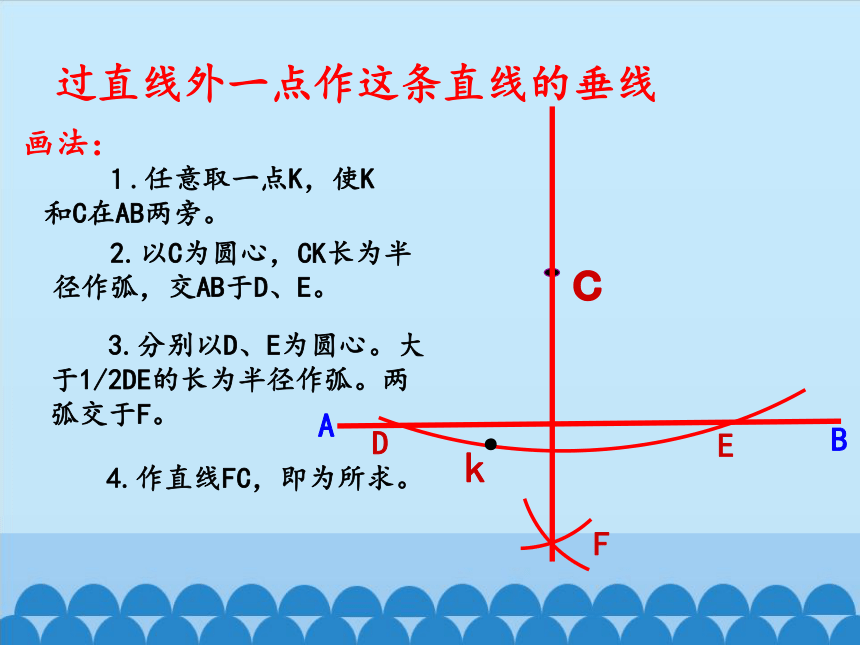
过直线外一点作这条直线的垂线
B
E
.
k
c
画法:
1.任意取一点K,使K和C在AB两旁。
3.分别以D、E为圆心。大于1/2DE的长为半径作弧。两弧交于F。
4.作直线FC,即为所求。
2.以C为圆心,CK长为半径作弧,交AB于D、E。
F
角平分线的性质
已知:如下图,OC是∠AOB的平分线,P是OC上任意一点,PD⊥OA,PE⊥OB,垂足分别为D,E。求证:PD=PE。
1
2
A
B
D
E
P
O
C
定理:角的平分线上的点到角的两边的距离相等。
∴PD=PE(全等三角形的对应边相等)。
证明:
∵ OC是∠AOB的平分线(已知),
∴∠1=∠2(角平分线的定义)。
∵PD⊥OA,PE⊥OB(已知),
∴∠PDO=∠PEO=90°(垂直的定义)。
在△PDO和△PEO中,
∠PDO=∠PEO (已证),
∠1=∠2(已证),
OP=OP(公共边),
∴△PDO≌△PEO (AAS)。
1
2
A
B
D
E
P
O
C
已知:如图,PD⊥OA,PE⊥OB,点D、E为垂足,PD=PE。求证:点P在∠AOB的平分线上。
O
C
B
1
A
2
P
D
E
证明:PD⊥OA,PE⊥OB,点D、E为垂足,
在Rt△PDO与Rt△PEO中
∴∠PDO=∠PEO=90°
PD=PE(已知)
{
OP=OP(公共边)
∴Rt△PDO≌△PDO
∴∠1=∠2即点P在∠AOB的平分线上。
反过来,到一个角的两边的距离相等的点是否一定在这个角的平分线上呢?
角平分线的判定定理:
角的内部到角两边的距离相等的点在这个角平分线上。
角平分线的性质定理和角平分线的判定定理是证明角相等、线段相等的新途径。
已知:如图,△ABC的角平分线BM、CN相交于点P。
求证:点P在∠BAC的角平分线上。
A
B
C
M
N
P
D
E
F
证明:
过点P作PD⊥AB于D,PE⊥BC于E,PF⊥AC于F,
∵BM是△ABC的角平分线,点P在BM上。
∴PD=PE(角平分线上的点到这个角的两边距离相等)
同理,PE=PF
∴PD=PF
∴AP平分∠BAC
已知:如图,△ABC的外角∠CBD和∠BCE的平分线相交于点F。求证:点F在∠DAE的平分线上。
C
D
A
B
F
E
O
Q
P
变式
1.画一个已知角的角平分线;
2.角平分线的性质:
角的平分线上的点到角的两边的距离相等。
3.角平分线的判定结论:
到角的两边的距离相等的点在角平分线上。
小结:
谢 谢
角的平分线
一条射线
把一个角
分成两个相等的角,
这条射线叫做这个角的平分线。
o
B
C
A
1
2
在半透明的纸上画∠BAC,对折,使角的两条边完全重合,然后用直尺画出折痕OD。
从上面试验可以看出,角是轴对称图形,对称轴是它的角平分线所在的直线。
B
C
A
D
不利用作图工具,请你将一张用纸片做的角分成两个相等的角。你有什么办法?
情景引入
如果前面活动中的纸片换成木板、钢板等没法折的角,又该怎么办呢?
用尺规作图的方法作出角的平分线。
探究
已知:如图,∠AOB。求作:∠AOB的平分线。
O
A
B
C
M
N
画法:
1.以O为圆心,适当长为半径作弧,交OA于M,交OB于N。
2.分别以M、N为圆心。大于1/2MN的长为半径作弧。两弧在∠AOB的内部交于C。
3.作射线OC。
射线OC即为所求。
B
A
.
C
E
D
过直线上一点作这条直线的垂线
画法:
1.以C为圆心,适当长为半径作弧,交AB于D,E。
2.分别以D,E为圆心。大于 1/2 DE的长为半径作弧。两弧交于F。
3.作直线FC,直线FC,即为所求。
F
A
D
过直线外一点作这条直线的垂线
B
E
.
k
c
画法:
1.任意取一点K,使K和C在AB两旁。
3.分别以D、E为圆心。大于1/2DE的长为半径作弧。两弧交于F。
4.作直线FC,即为所求。
2.以C为圆心,CK长为半径作弧,交AB于D、E。
F
角平分线的性质
已知:如下图,OC是∠AOB的平分线,P是OC上任意一点,PD⊥OA,PE⊥OB,垂足分别为D,E。求证:PD=PE。
1
2
A
B
D
E
P
O
C
定理:角的平分线上的点到角的两边的距离相等。
∴PD=PE(全等三角形的对应边相等)。
证明:
∵ OC是∠AOB的平分线(已知),
∴∠1=∠2(角平分线的定义)。
∵PD⊥OA,PE⊥OB(已知),
∴∠PDO=∠PEO=90°(垂直的定义)。
在△PDO和△PEO中,
∠PDO=∠PEO (已证),
∠1=∠2(已证),
OP=OP(公共边),
∴△PDO≌△PEO (AAS)。
1
2
A
B
D
E
P
O
C
已知:如图,PD⊥OA,PE⊥OB,点D、E为垂足,PD=PE。求证:点P在∠AOB的平分线上。
O
C
B
1
A
2
P
D
E
证明:PD⊥OA,PE⊥OB,点D、E为垂足,
在Rt△PDO与Rt△PEO中
∴∠PDO=∠PEO=90°
PD=PE(已知)
{
OP=OP(公共边)
∴Rt△PDO≌△PDO
∴∠1=∠2即点P在∠AOB的平分线上。
反过来,到一个角的两边的距离相等的点是否一定在这个角的平分线上呢?
角平分线的判定定理:
角的内部到角两边的距离相等的点在这个角平分线上。
角平分线的性质定理和角平分线的判定定理是证明角相等、线段相等的新途径。
已知:如图,△ABC的角平分线BM、CN相交于点P。
求证:点P在∠BAC的角平分线上。
A
B
C
M
N
P
D
E
F
证明:
过点P作PD⊥AB于D,PE⊥BC于E,PF⊥AC于F,
∵BM是△ABC的角平分线,点P在BM上。
∴PD=PE(角平分线上的点到这个角的两边距离相等)
同理,PE=PF
∴PD=PF
∴AP平分∠BAC
已知:如图,△ABC的外角∠CBD和∠BCE的平分线相交于点F。求证:点F在∠DAE的平分线上。
C
D
A
B
F
E
O
Q
P
变式
1.画一个已知角的角平分线;
2.角平分线的性质:
角的平分线上的点到角的两边的距离相等。
3.角平分线的判定结论:
到角的两边的距离相等的点在角平分线上。
小结:
谢 谢
