人教版 八年级数学上册13.3.1等腰三角形同步习题(word版含解析)
文档属性
| 名称 | 人教版 八年级数学上册13.3.1等腰三角形同步习题(word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 408.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-27 11:20:36 | ||
图片预览



文档简介
2021-2022学年初中数学八年级上册(人教版)
13.3.1等腰三角形-同步习题
时间:40分钟
一、单选题
1.如图,中,,D、E分别是两点,且,连接.则的度数为( )度·
A.45 B.52.5 C.67.5 D.75
2.如图,在中,于点D,则等于( )
A. B. C. D.
3.如图所示的正方形网格中,网格线的交点称为格点.已知、是两格点,若也是图中的格点, 则使得是以为一腰的等腰三角形时, 点的个数是( )
A.8 B.6 C.4 D.7
4.下列能断定△ABC为等腰三角形的是( )
A.∠A=40°,∠B=50° B.∠A=2∠B=70°
C.∠A=40°,∠B=70° D.AB=3,BC=6,周长为14
5.要使得△ABC是等腰三角形,则需要满足下列条件中的( )
A.∠A=50°,∠B=60° B.∠A=50°,∠B=100°
C.∠A+∠B=90° D.∠A+∠B=90°
二、填空题
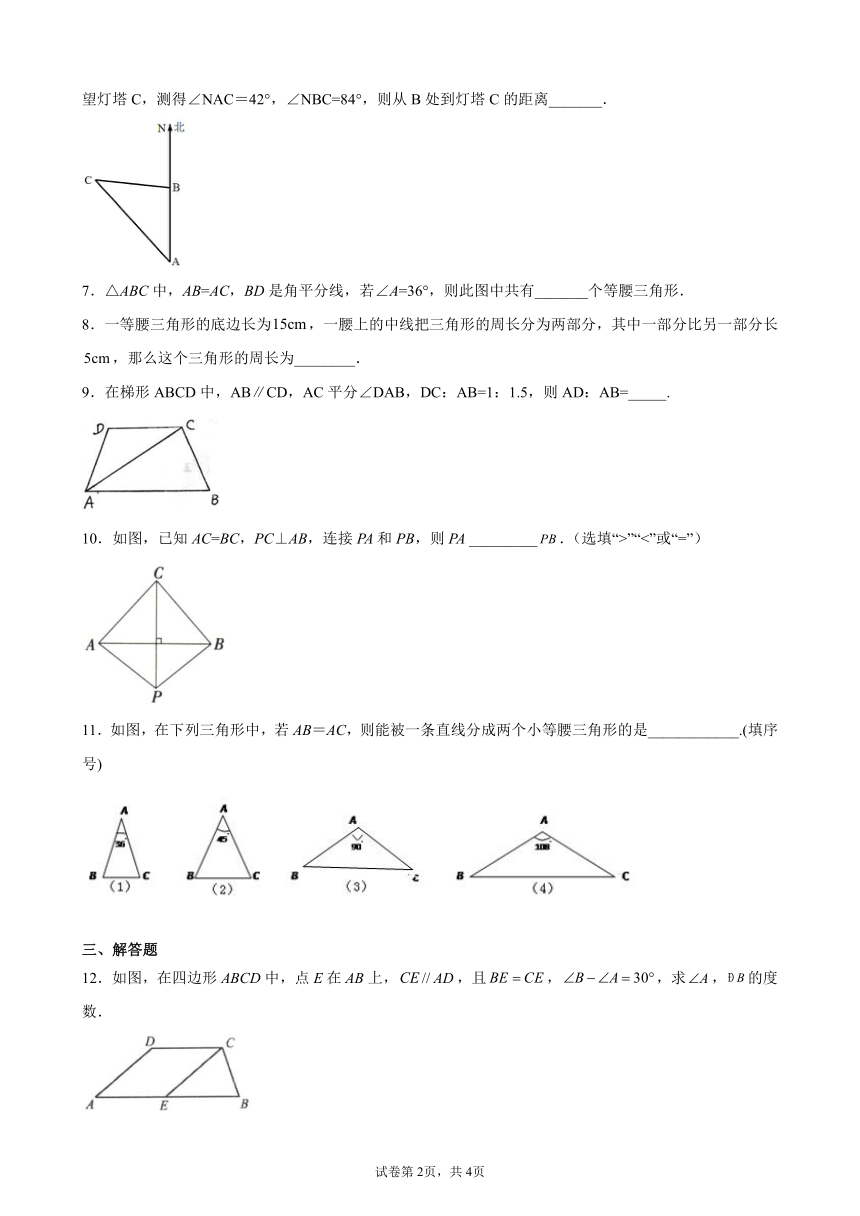
6.如图,上午8时,一条船从A处出发,以15海里/时的速度向正北航行,10时到达B处,从A、B望灯塔C,测得∠NAC=42°,∠NBC=84°,则从B处到灯塔C的距离_______.
7.△ABC中,AB=AC,BD是角平分线,若∠A=36°,则此图中共有_______个等腰三角形.
8.一等腰三角形的底边长为,一腰上的中线把三角形的周长分为两部分,其中一部分比另一部分长,那么这个三角形的周长为________.
9.在梯形ABCD中,AB∥CD,AC平分∠DAB,DC:AB=1:1.5,则AD:AB=_____.
10.如图,已知AC=BC,PC⊥AB,连接PA和PB,则PA _________.(选填“>”“<”或“=”)
11.如图,在下列三角形中,若AB=AC,则能被一条直线分成两个小等腰三角形的是____________.(填序号)
三、解答题
12.如图,在四边形ABCD中,点E在AB上,//,且,,求,的度数.
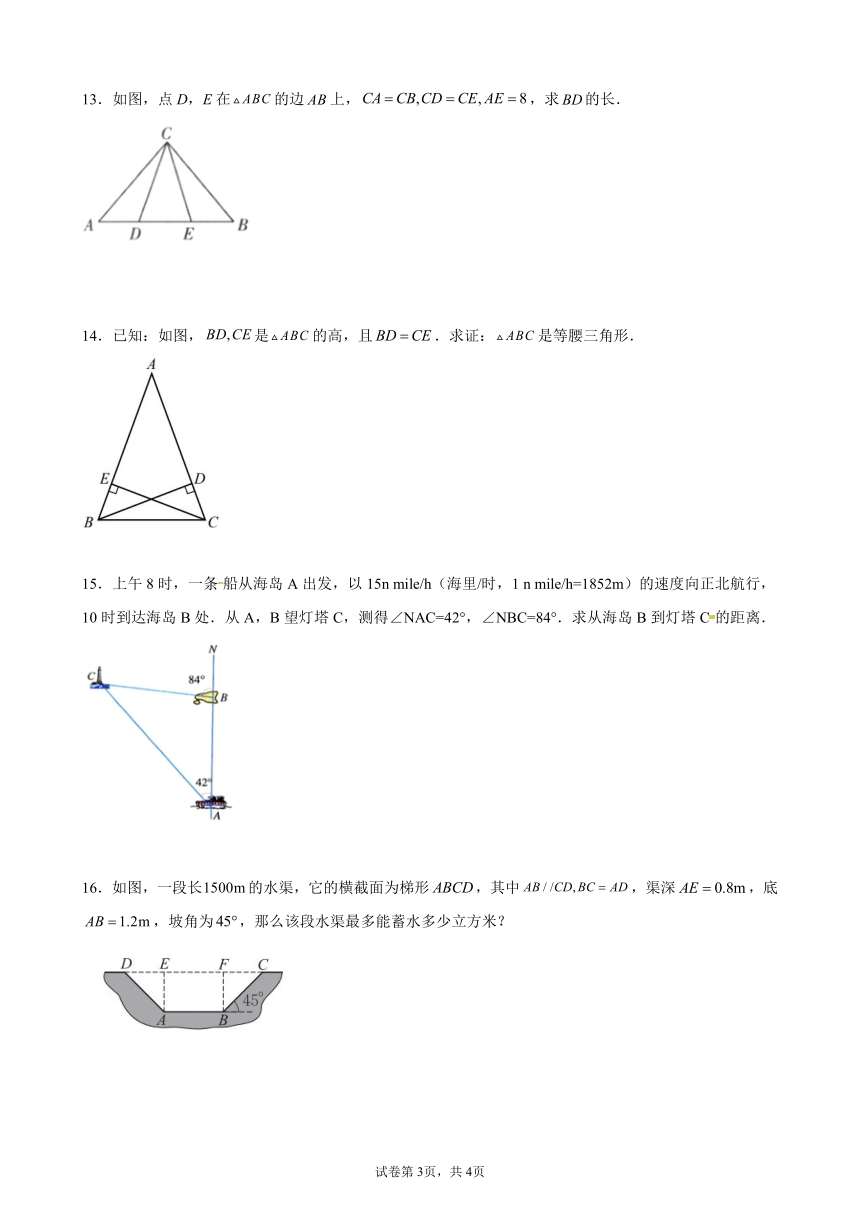
13.如图,点D,E在的边上,,求的长.
14.已知:如图,是的高,且.求证:是等腰三角形.
15.上午8时,一条船从海岛A出发,以15n mile/h(海里/时,1 n mile/h=1852m)的速度向正北航行,10时到达海岛B处.从A,B望灯塔C,测得∠NAC=42°,∠NBC=84°.求从海岛B到灯塔C的距离.
16.如图,一段长的水渠,它的横截面为梯形,其中,渠深,底,坡角为,那么该段水渠最多能蓄水多少立方米?
17.如图,在和中,为斜边,,、相交于点.
(1)请说明的理由;
(2)若,,求的长.
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.C
【解析】解:∵AB=AC,
∴∠ABC=∠C,
∵∠ABC+∠C+∠A=180°,∠A=30°,
∴∠ABC=∠C=75°,
∵BD=BC=DE,
∴∠BED=∠BDE,∠BCD=∠BDC=75°,
∴∠DBC=180°-∠BCD-∠BDC=30°,
∴∠DBE=45°,
∴ ,
故选C.
2.D
【解析】解:∵在中,,
∴是的平分线,
∵,
∴,
故选D.
3.C
【解析】解:如图,当AB为等腰△ABC其中的一条腰时,符合条件的C点有4个,
故选:C.
4.C
【解析】A. ∠C=180° 40° 50°=90°,没有相等的角,则不是等腰三角形,本选项错误;
B、∵∠A=2∠B=70°,
∴∠B=35°,
∴∠C=75°,没有相等的角,则不是等腰三角形,本选项错误;
C、∠C=180° 40° 70°=70°,有相等的角,则是等腰三角形,本选项正确;
D、∵AB=3,BC=6,周长为14,
∴AC=14 6 3=5,没有相等的边,则不是等腰三角形,本选项错误;
故选C.
5.D
【解析】解:A、∵∠A=50°,∠B=60°,
∴∠C=180°-∠A-∠B=70°,
所以∠A≠∠B≠∠C,
所以△ABC不是等腰三角形;
B、∵∠A=50°,∠B=100°,
∴∠C=180°-∠A-∠B=30°,
所以∠A≠∠B≠∠C,
所以△ABC不是等腰三角形;
C、∠A+∠B=90°不能判定△ABC是等腰三角形;
D、∠A+∠B=90°,
则2∠A+∠B=180°,
∵∠A+∠B+∠C=180°,
∴∠A=∠C,
所以△ABC是等腰三角形.
故选D.
6.30海里
【解析】根据题意得:AB=2×15=30(海里),
∵∠NAC=42°,∠NBC=84°,
∴∠C=∠NBC ∠NAC=42°,
∴∠C=∠NAC,
∴BC=AB=30海里.
即从海岛B到灯塔C的距离是30海里.
故答案为30海里.
7.3
【解析】解:∵AB=AC,∠A=36°,
∴∠ABC=∠ACB,
∵∠ABC=∠ACB==72°,BD是∠ABC的角的平分线,
∴∠ABD=∠DBC=∠ABC=36°=∠A,
∴AD=BD,BCE=36°,
∵∠DBC=36°,∠ACD=72°,∠BDC=180°-72°-36°=72°,
∴BD=BC,
∴△ABC,△ADB,△BDC都是等腰三角形,共3个.
故答案为:3.
8.或
【解析】解:如图,为等腰三角形,
设 则
当时,
解得:
当时,
解得:
故答案为:或
9.1:1.5
【解析】解:∵AB∥CD
∴∠DCA=∠CAB
∵AC平分∠DAB
∴∠CAB=∠CAD =∠DCA
∴AD = CD
∵DC∶AB=1∶1.5
∴AD∶AB=1∶1.5
10.=
【解析】解:∵AC=BC,PC⊥AB,
∴PC垂直平分AB(等腰三角形三线合一),
∴PA=PB(线段垂直平分线上的点到线段两端点的距离相等).
故答案为:=.
11.(1)(3)(4)
【解析】由题意知,要求“被一条直线分成两个小等腰三角形”,
(1)中分成的两个等腰三角形的角的度数分别为:36°,36°,108°和36°,72°72°;
(2)不能;
(3)直角三角形的斜边上的中线把它还分为了两个等腰三角形;
(4)中分成的为36°,72°,72°和36°,36°,108°.
故应填①③④.
12.,.
【解析】∵ ,
∴∠BEC=∠A,
在△ECB中,∵BE=CE,
∴∠B=∠BCE,
∵∠B+∠BCE+∠BEC=180°,即2∠B+∠A=180°,
联立∠B-∠A=30°,
解得∠A=40°,∠B=70°.
13.
【解析】解:如图,过C作,垂足为M.
∵,,且,
∴,
∴,
∴.
∵,
∴.
14.证明见解析
【解析】解: 是的高,
是等腰三角形.
15.从海岛B到灯塔C的距离是30海里
【解析】解:根据题意得:
AB=2×15=30(海里),
∵∠NAC=42°,∠NBC=84°,
∴∠C=∠NBC﹣∠NAC=42°,
∴∠C=∠NAC,
∴BC=AB=30海里.
答:从海岛B到灯塔C的距离是30海里
16..
【解析】解:∵,
∴梯形是一个等腰梯形
∵,,坡角为,
∴,,
∴
∴
∴该段水渠最多能蓄水为:.
17.(1)见解析;(2)CE=1.
【解析】(1)证明:在和中,
∵与是对顶角,
∴.
∵,,
∴≌(AAS).
∴.
(2)∵,,
∴,
∴ ,
∴.
答案第1页,共2页
答案第1页,共2页
13.3.1等腰三角形-同步习题
时间:40分钟
一、单选题
1.如图,中,,D、E分别是两点,且,连接.则的度数为( )度·
A.45 B.52.5 C.67.5 D.75
2.如图,在中,于点D,则等于( )
A. B. C. D.
3.如图所示的正方形网格中,网格线的交点称为格点.已知、是两格点,若也是图中的格点, 则使得是以为一腰的等腰三角形时, 点的个数是( )
A.8 B.6 C.4 D.7
4.下列能断定△ABC为等腰三角形的是( )
A.∠A=40°,∠B=50° B.∠A=2∠B=70°
C.∠A=40°,∠B=70° D.AB=3,BC=6,周长为14
5.要使得△ABC是等腰三角形,则需要满足下列条件中的( )
A.∠A=50°,∠B=60° B.∠A=50°,∠B=100°
C.∠A+∠B=90° D.∠A+∠B=90°
二、填空题
6.如图,上午8时,一条船从A处出发,以15海里/时的速度向正北航行,10时到达B处,从A、B望灯塔C,测得∠NAC=42°,∠NBC=84°,则从B处到灯塔C的距离_______.
7.△ABC中,AB=AC,BD是角平分线,若∠A=36°,则此图中共有_______个等腰三角形.
8.一等腰三角形的底边长为,一腰上的中线把三角形的周长分为两部分,其中一部分比另一部分长,那么这个三角形的周长为________.
9.在梯形ABCD中,AB∥CD,AC平分∠DAB,DC:AB=1:1.5,则AD:AB=_____.
10.如图,已知AC=BC,PC⊥AB,连接PA和PB,则PA _________.(选填“>”“<”或“=”)
11.如图,在下列三角形中,若AB=AC,则能被一条直线分成两个小等腰三角形的是____________.(填序号)
三、解答题
12.如图,在四边形ABCD中,点E在AB上,//,且,,求,的度数.
13.如图,点D,E在的边上,,求的长.
14.已知:如图,是的高,且.求证:是等腰三角形.
15.上午8时,一条船从海岛A出发,以15n mile/h(海里/时,1 n mile/h=1852m)的速度向正北航行,10时到达海岛B处.从A,B望灯塔C,测得∠NAC=42°,∠NBC=84°.求从海岛B到灯塔C的距离.
16.如图,一段长的水渠,它的横截面为梯形,其中,渠深,底,坡角为,那么该段水渠最多能蓄水多少立方米?
17.如图,在和中,为斜边,,、相交于点.
(1)请说明的理由;
(2)若,,求的长.
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.C
【解析】解:∵AB=AC,
∴∠ABC=∠C,
∵∠ABC+∠C+∠A=180°,∠A=30°,
∴∠ABC=∠C=75°,
∵BD=BC=DE,
∴∠BED=∠BDE,∠BCD=∠BDC=75°,
∴∠DBC=180°-∠BCD-∠BDC=30°,
∴∠DBE=45°,
∴ ,
故选C.
2.D
【解析】解:∵在中,,
∴是的平分线,
∵,
∴,
故选D.
3.C
【解析】解:如图,当AB为等腰△ABC其中的一条腰时,符合条件的C点有4个,
故选:C.
4.C
【解析】A. ∠C=180° 40° 50°=90°,没有相等的角,则不是等腰三角形,本选项错误;
B、∵∠A=2∠B=70°,
∴∠B=35°,
∴∠C=75°,没有相等的角,则不是等腰三角形,本选项错误;
C、∠C=180° 40° 70°=70°,有相等的角,则是等腰三角形,本选项正确;
D、∵AB=3,BC=6,周长为14,
∴AC=14 6 3=5,没有相等的边,则不是等腰三角形,本选项错误;
故选C.
5.D
【解析】解:A、∵∠A=50°,∠B=60°,
∴∠C=180°-∠A-∠B=70°,
所以∠A≠∠B≠∠C,
所以△ABC不是等腰三角形;
B、∵∠A=50°,∠B=100°,
∴∠C=180°-∠A-∠B=30°,
所以∠A≠∠B≠∠C,
所以△ABC不是等腰三角形;
C、∠A+∠B=90°不能判定△ABC是等腰三角形;
D、∠A+∠B=90°,
则2∠A+∠B=180°,
∵∠A+∠B+∠C=180°,
∴∠A=∠C,
所以△ABC是等腰三角形.
故选D.
6.30海里
【解析】根据题意得:AB=2×15=30(海里),
∵∠NAC=42°,∠NBC=84°,
∴∠C=∠NBC ∠NAC=42°,
∴∠C=∠NAC,
∴BC=AB=30海里.
即从海岛B到灯塔C的距离是30海里.
故答案为30海里.
7.3
【解析】解:∵AB=AC,∠A=36°,
∴∠ABC=∠ACB,
∵∠ABC=∠ACB==72°,BD是∠ABC的角的平分线,
∴∠ABD=∠DBC=∠ABC=36°=∠A,
∴AD=BD,BCE=36°,
∵∠DBC=36°,∠ACD=72°,∠BDC=180°-72°-36°=72°,
∴BD=BC,
∴△ABC,△ADB,△BDC都是等腰三角形,共3个.
故答案为:3.
8.或
【解析】解:如图,为等腰三角形,
设 则
当时,
解得:
当时,
解得:
故答案为:或
9.1:1.5
【解析】解:∵AB∥CD
∴∠DCA=∠CAB
∵AC平分∠DAB
∴∠CAB=∠CAD =∠DCA
∴AD = CD
∵DC∶AB=1∶1.5
∴AD∶AB=1∶1.5
10.=
【解析】解:∵AC=BC,PC⊥AB,
∴PC垂直平分AB(等腰三角形三线合一),
∴PA=PB(线段垂直平分线上的点到线段两端点的距离相等).
故答案为:=.
11.(1)(3)(4)
【解析】由题意知,要求“被一条直线分成两个小等腰三角形”,
(1)中分成的两个等腰三角形的角的度数分别为:36°,36°,108°和36°,72°72°;
(2)不能;
(3)直角三角形的斜边上的中线把它还分为了两个等腰三角形;
(4)中分成的为36°,72°,72°和36°,36°,108°.
故应填①③④.
12.,.
【解析】∵ ,
∴∠BEC=∠A,
在△ECB中,∵BE=CE,
∴∠B=∠BCE,
∵∠B+∠BCE+∠BEC=180°,即2∠B+∠A=180°,
联立∠B-∠A=30°,
解得∠A=40°,∠B=70°.
13.
【解析】解:如图,过C作,垂足为M.
∵,,且,
∴,
∴,
∴.
∵,
∴.
14.证明见解析
【解析】解: 是的高,
是等腰三角形.
15.从海岛B到灯塔C的距离是30海里
【解析】解:根据题意得:
AB=2×15=30(海里),
∵∠NAC=42°,∠NBC=84°,
∴∠C=∠NBC﹣∠NAC=42°,
∴∠C=∠NAC,
∴BC=AB=30海里.
答:从海岛B到灯塔C的距离是30海里
16..
【解析】解:∵,
∴梯形是一个等腰梯形
∵,,坡角为,
∴,,
∴
∴
∴该段水渠最多能蓄水为:.
17.(1)见解析;(2)CE=1.
【解析】(1)证明:在和中,
∵与是对顶角,
∴.
∵,,
∴≌(AAS).
∴.
(2)∵,,
∴,
∴ ,
∴.
答案第1页,共2页
答案第1页,共2页
