人教版八年级数学上册13.4课题学习最短路径问题同步习题(word版含解析)
文档属性
| 名称 | 人教版八年级数学上册13.4课题学习最短路径问题同步习题(word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 478.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-27 11:32:18 | ||
图片预览



文档简介
2021-2022学年初中数学八年级上册(人教版)
13.4课题学习最短路径问题-同步习题
时间:40分钟
一、单选题
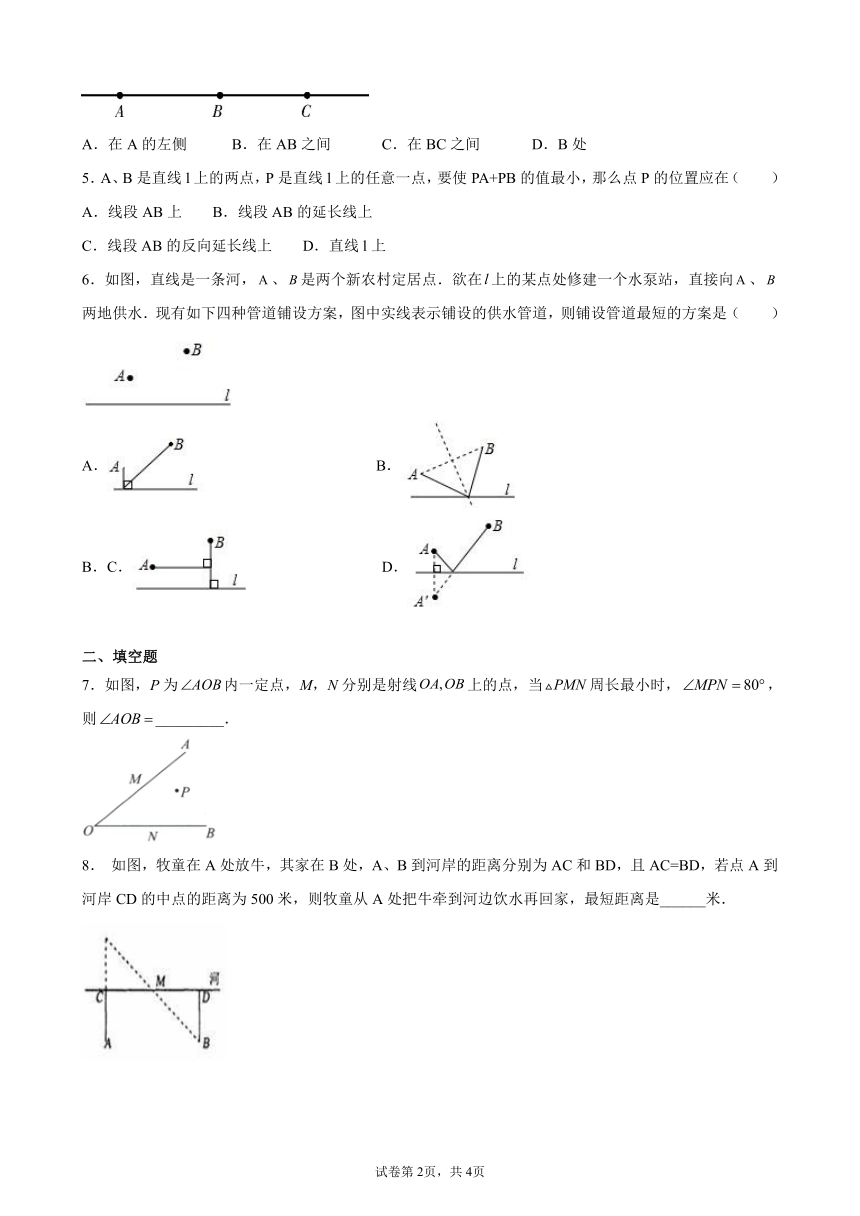
1.如图所示,直线l是一条河的河岸,P,Q是河同侧的水产的生产基地,现从河岸某点M处分别派出两辆水产车运送水产如下有四种运输方案,则运输路程合理且最短的是( )
A. B.
C. D.
2.如图,A是直线l外一点,点B,E,D,C在直线l上,且,D为垂足,如果量得,,,,则点A到直线l的距离为( )
A.11 cm B.7 cm C.6 cm D.5 cm
3.为解决村庄灌溉问题,政府投资由水库向A,B,C,D这四个村庄铺设管道,现已知这四个村庄与水库以及村与村之间的距离(单位:km)如图所示,则把水库的水输送到这四个村庄铺设管道的总长度最短应是( )
A.16km B.17km C.18km D.20km
4.A,B,C三个车站在东西方向笔直的一条公路上,现要建一个加油站使其到三个车站的距离和最小,则加油站应建在( )
A.在A的左侧 B.在AB之间 C.在BC之间 D.B处
5.A、B是直线l上的两点,P是直线l上的任意一点,要使PA+PB的值最小,那么点P的位置应在( )
A.线段AB上 B.线段AB的延长线上
C.线段AB的反向延长线上 D.直线l上
6.如图,直线是一条河,、是两个新农村定居点.欲在上的某点处修建一个水泵站,直接向、两地供水.现有如下四种管道铺设方案,图中实线表示铺设的供水管道,则铺设管道最短的方案是( )
B.
C. D.
二、填空题
7.如图,P为内一定点,M,N分别是射线上的点,当周长最小时,,则_________.
8. 如图,牧童在A处放牛,其家在B处,A、B到河岸的距离分别为AC和BD,且AC=BD,若点A到河岸CD的中点的距离为500米,则牧童从A处把牛牵到河边饮水再回家,最短距离是______米.
三、解答题
9.如图,在旷野上,一个人骑着马从A地到B地,半路上他必须让马先到河岸l的P点去饮水,然后再让马到河岸m的Q点再次饮水,最后到达B点,他应该如何选择马饮水地点P、Q,才能使所走路程最短?(假设河岸l、m为直线)
10.某班举行文艺晚会,桌子摆成两条直线(),桌面上摆满了橘子,桌面上摆满了糖果,坐在C处的小明先拿橘子再拿糖果,然后回到座位,请你帮他设计路线,使其行走的总路程最短.(保留作图痕迹)
11.如图,一只妈蚁要从正方体的一个顶点A沿表面爬行到顶点B,怎样爬行路线最短?如果要爬行到顶点C呢?说出你的理由.
12.如图所示,在一条河的两岸有两个村庄,现在要在河上建一座小桥,桥的方向与河岸垂直,设河的宽度不变,试问:桥建在何处,才能使从A到B的距离最短?保留作图痕迹并说明理由.
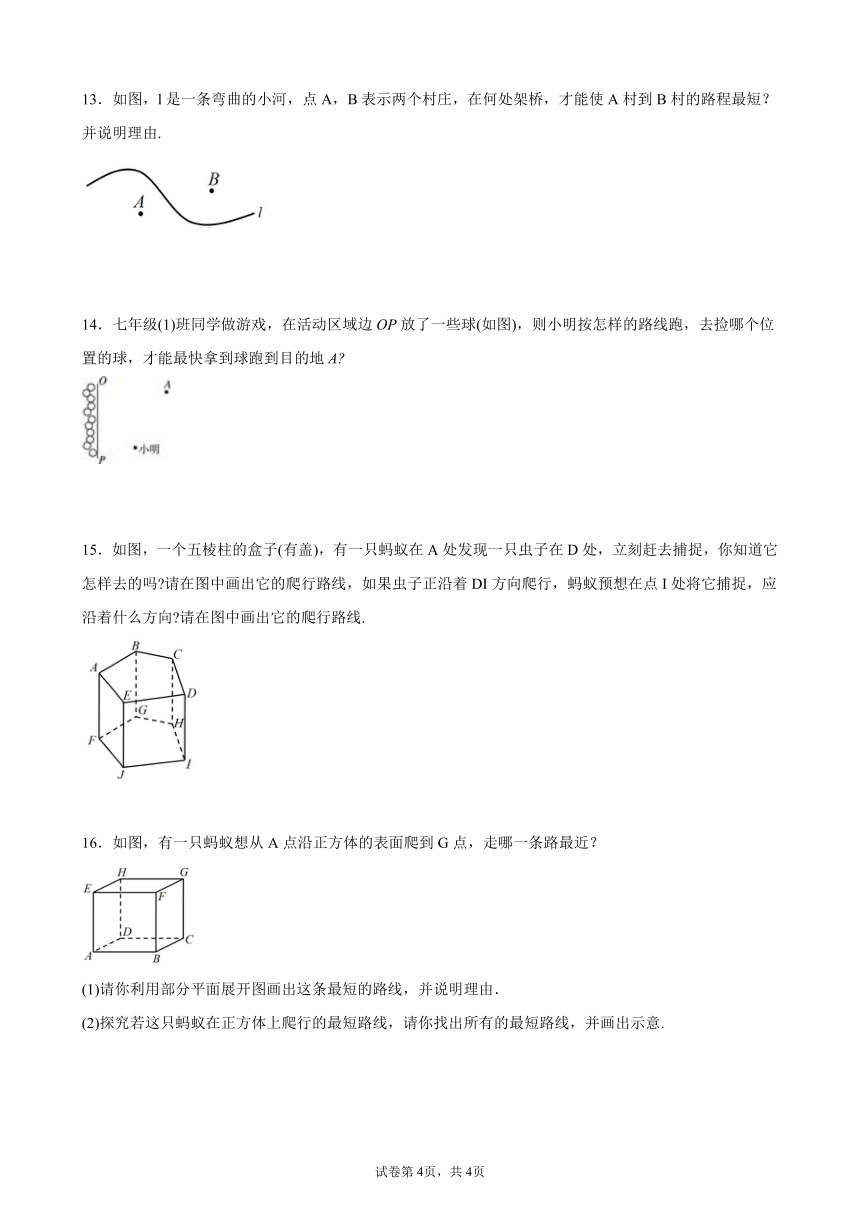
13.如图,l是一条弯曲的小河,点A,B表示两个村庄,在何处架桥,才能使A村到B村的路程最短?并说明理由.
14.七年级(1)班同学做游戏,在活动区域边OP放了一些球(如图),则小明按怎样的路线跑,去捡哪个位置的球,才能最快拿到球跑到目的地A
15.如图,一个五棱柱的盒子(有盖),有一只蚂蚁在A处发现一只虫子在D处,立刻赶去捕捉,你知道它怎样去的吗 请在图中画出它的爬行路线,如果虫子正沿着DI方向爬行,蚂蚁预想在点I处将它捕捉,应沿着什么方向 请在图中画出它的爬行路线.
16.如图,有一只蚂蚁想从A点沿正方体的表面爬到G点,走哪一条路最近?
(1)请你利用部分平面展开图画出这条最短的路线,并说明理由.
(2)探究若这只蚂蚁在正方体上爬行的最短路线,请你找出所有的最短路线,并画出示意.
试卷第2页,共2页
试卷第1页,共1页
参考答案
1.B
【解析】根据“将军饮马”模型求最短路线题型,作点P关于直线l的对称点,连接Q交直线l于点M,利用两点之间线段最短和线段垂直平分线的性质作图即可,
故选:B.
2.D
【解析】∵AD=5cm,∴点A到直线l的距离是5cm.
故选D.
3.A
【解析】最短总长度应该是:水库到A,再从A到B、D,然后从D到C,总长度为:4+5+3+4=16(km).
故选A.
4.D
【解析】设P、B的距离为xkm,
如图1:
路程之和为PA+PC+PB=(AC+x)km;
如图2:
路程之和为PA+PC+PB=(AC+x)km;
综上所述:路程之和为=(AC+x)km,
当x=0时,路程之和为AC的长度,则加油站应建在B处.
故选D
5.A
【解析】当P点在线段AB的延长线上,则PA+PB=PB+AB+PB=AB+2PB;
当P点在线段AB的反向延长线上,则PA+PB=PA+AB+PB=AB+2PA;
当P点在线段AB上,则PA+PB=AB,
所以当P点在线段AB上时PA+PB的值最小.
故选:A.
6.D
【解析】解:作点A关于直线l的对称点,然后连接与直线l交于一点,在这点修建水泵站,
根据轴对称的性质和连点之间线段最短的性质可以证明此事铺设的管道最短.
故选:D.
7.50°
【解析】如图,作P关于,的对称点,连接.则当M,N是与的交点时,的周长最小.
∵P,关于对称,,
∴,.
同理,,,
∴.
∵,∴,
∴,∴.
故答案为:
8.1000
【解析】
作出A的对称点A′,连接A′B与CD相交于M,则牧童从A处把牛牵到河边饮水再回家,最短距离是A′B的长.易得△A′CM≌△BDM,AC=BD,所以A′C=BD,则A′C /BD ="CM" /MD ,
所以CM=DM,M为CD的中点,
由于A到河岸CD的中点的距离为500米,
所以A′到M的距离为500米,
A′B=1000米.
故最短距离是1000米.
9.见解析
【解析】解:如图所示,分别作点A关于直线l的对称点,点B关于直线m的对称点,连接,分别交l,m于点P,Q,连接、,则路程最短.
.
10.见解析
【解析】如图所示,小明的行走路线为,此时所走的总路程为的长,总路程最短.
11.见解析
【解析】解:如图,
由于“两点之间,线段最短”,因此,小蚂蚁要从顶点A爬行到顶点B,只需沿线段爬行即可.
如果要爬行到顶点C,有三种情况.
若蚂蚁爬行经过面,可将这个正方体展开,在展开图上连接,与棱a(或b)交于点(或),小蚂蚁沿线段(或)爬行,路线最短.
类似地,蚂蚁经过面和爬行到顶点C,也分别有两条最短路线.
因此,蚂蚁爬行的最短路线有6条.
12.见解析
【解析】如图,作垂直于河岸,使等于河宽,连接,与河岸相交于P,作,交于点D,则且.连接,利用平行四边形的性质可知.根据“两点之间,线段最短”,可知最短,即从A到B,路径最短,故桥应建在处.
13.点P处架桥,才能使A村到B村的路程最短,见解析.
【解析】连结AB交l于点P.
在点P处架桥,才能使A村到B村的路程最短.
理由:两点之间线段最短.
14.见解析
【解析】如图,作小明关于活动区域边线OP的对称点A′,连接AA′交OP于点B,则小明行走的路线是小明→B→A,即在B处捡球,才能最快拿到球跑到目的地A.
15.第一问:如图沿线段AD爬行;第二问取线段EJ的中点M,连结AM和MI,此路线为蚂蚁爬行的路线.
【解析】解:第一问:如图沿线段AD爬行;
第二问取线段EJ的中点M,连结AM和MI,此路线为蚂蚁爬行的路线.
理由都是:两点之间线段最短.
16.如图①,(1)见解析,理由:两点之间线段最短;(2)见解析.
【解析】(1)如图①,理由:两点之间线段最短.
(2)如图②,这种最短路线有4条.
答案第1页,共2页
答案第1页,共2页
13.4课题学习最短路径问题-同步习题
时间:40分钟
一、单选题
1.如图所示,直线l是一条河的河岸,P,Q是河同侧的水产的生产基地,现从河岸某点M处分别派出两辆水产车运送水产如下有四种运输方案,则运输路程合理且最短的是( )
A. B.
C. D.
2.如图,A是直线l外一点,点B,E,D,C在直线l上,且,D为垂足,如果量得,,,,则点A到直线l的距离为( )
A.11 cm B.7 cm C.6 cm D.5 cm
3.为解决村庄灌溉问题,政府投资由水库向A,B,C,D这四个村庄铺设管道,现已知这四个村庄与水库以及村与村之间的距离(单位:km)如图所示,则把水库的水输送到这四个村庄铺设管道的总长度最短应是( )
A.16km B.17km C.18km D.20km
4.A,B,C三个车站在东西方向笔直的一条公路上,现要建一个加油站使其到三个车站的距离和最小,则加油站应建在( )
A.在A的左侧 B.在AB之间 C.在BC之间 D.B处
5.A、B是直线l上的两点,P是直线l上的任意一点,要使PA+PB的值最小,那么点P的位置应在( )
A.线段AB上 B.线段AB的延长线上
C.线段AB的反向延长线上 D.直线l上
6.如图,直线是一条河,、是两个新农村定居点.欲在上的某点处修建一个水泵站,直接向、两地供水.现有如下四种管道铺设方案,图中实线表示铺设的供水管道,则铺设管道最短的方案是( )
B.
C. D.
二、填空题
7.如图,P为内一定点,M,N分别是射线上的点,当周长最小时,,则_________.
8. 如图,牧童在A处放牛,其家在B处,A、B到河岸的距离分别为AC和BD,且AC=BD,若点A到河岸CD的中点的距离为500米,则牧童从A处把牛牵到河边饮水再回家,最短距离是______米.
三、解答题
9.如图,在旷野上,一个人骑着马从A地到B地,半路上他必须让马先到河岸l的P点去饮水,然后再让马到河岸m的Q点再次饮水,最后到达B点,他应该如何选择马饮水地点P、Q,才能使所走路程最短?(假设河岸l、m为直线)
10.某班举行文艺晚会,桌子摆成两条直线(),桌面上摆满了橘子,桌面上摆满了糖果,坐在C处的小明先拿橘子再拿糖果,然后回到座位,请你帮他设计路线,使其行走的总路程最短.(保留作图痕迹)
11.如图,一只妈蚁要从正方体的一个顶点A沿表面爬行到顶点B,怎样爬行路线最短?如果要爬行到顶点C呢?说出你的理由.
12.如图所示,在一条河的两岸有两个村庄,现在要在河上建一座小桥,桥的方向与河岸垂直,设河的宽度不变,试问:桥建在何处,才能使从A到B的距离最短?保留作图痕迹并说明理由.
13.如图,l是一条弯曲的小河,点A,B表示两个村庄,在何处架桥,才能使A村到B村的路程最短?并说明理由.
14.七年级(1)班同学做游戏,在活动区域边OP放了一些球(如图),则小明按怎样的路线跑,去捡哪个位置的球,才能最快拿到球跑到目的地A
15.如图,一个五棱柱的盒子(有盖),有一只蚂蚁在A处发现一只虫子在D处,立刻赶去捕捉,你知道它怎样去的吗 请在图中画出它的爬行路线,如果虫子正沿着DI方向爬行,蚂蚁预想在点I处将它捕捉,应沿着什么方向 请在图中画出它的爬行路线.
16.如图,有一只蚂蚁想从A点沿正方体的表面爬到G点,走哪一条路最近?
(1)请你利用部分平面展开图画出这条最短的路线,并说明理由.
(2)探究若这只蚂蚁在正方体上爬行的最短路线,请你找出所有的最短路线,并画出示意.
试卷第2页,共2页
试卷第1页,共1页
参考答案
1.B
【解析】根据“将军饮马”模型求最短路线题型,作点P关于直线l的对称点,连接Q交直线l于点M,利用两点之间线段最短和线段垂直平分线的性质作图即可,
故选:B.
2.D
【解析】∵AD=5cm,∴点A到直线l的距离是5cm.
故选D.
3.A
【解析】最短总长度应该是:水库到A,再从A到B、D,然后从D到C,总长度为:4+5+3+4=16(km).
故选A.
4.D
【解析】设P、B的距离为xkm,
如图1:
路程之和为PA+PC+PB=(AC+x)km;
如图2:
路程之和为PA+PC+PB=(AC+x)km;
综上所述:路程之和为=(AC+x)km,
当x=0时,路程之和为AC的长度,则加油站应建在B处.
故选D
5.A
【解析】当P点在线段AB的延长线上,则PA+PB=PB+AB+PB=AB+2PB;
当P点在线段AB的反向延长线上,则PA+PB=PA+AB+PB=AB+2PA;
当P点在线段AB上,则PA+PB=AB,
所以当P点在线段AB上时PA+PB的值最小.
故选:A.
6.D
【解析】解:作点A关于直线l的对称点,然后连接与直线l交于一点,在这点修建水泵站,
根据轴对称的性质和连点之间线段最短的性质可以证明此事铺设的管道最短.
故选:D.
7.50°
【解析】如图,作P关于,的对称点,连接.则当M,N是与的交点时,的周长最小.
∵P,关于对称,,
∴,.
同理,,,
∴.
∵,∴,
∴,∴.
故答案为:
8.1000
【解析】
作出A的对称点A′,连接A′B与CD相交于M,则牧童从A处把牛牵到河边饮水再回家,最短距离是A′B的长.易得△A′CM≌△BDM,AC=BD,所以A′C=BD,则A′C /BD ="CM" /MD ,
所以CM=DM,M为CD的中点,
由于A到河岸CD的中点的距离为500米,
所以A′到M的距离为500米,
A′B=1000米.
故最短距离是1000米.
9.见解析
【解析】解:如图所示,分别作点A关于直线l的对称点,点B关于直线m的对称点,连接,分别交l,m于点P,Q,连接、,则路程最短.
.
10.见解析
【解析】如图所示,小明的行走路线为,此时所走的总路程为的长,总路程最短.
11.见解析
【解析】解:如图,
由于“两点之间,线段最短”,因此,小蚂蚁要从顶点A爬行到顶点B,只需沿线段爬行即可.
如果要爬行到顶点C,有三种情况.
若蚂蚁爬行经过面,可将这个正方体展开,在展开图上连接,与棱a(或b)交于点(或),小蚂蚁沿线段(或)爬行,路线最短.
类似地,蚂蚁经过面和爬行到顶点C,也分别有两条最短路线.
因此,蚂蚁爬行的最短路线有6条.
12.见解析
【解析】如图,作垂直于河岸,使等于河宽,连接,与河岸相交于P,作,交于点D,则且.连接,利用平行四边形的性质可知.根据“两点之间,线段最短”,可知最短,即从A到B,路径最短,故桥应建在处.
13.点P处架桥,才能使A村到B村的路程最短,见解析.
【解析】连结AB交l于点P.
在点P处架桥,才能使A村到B村的路程最短.
理由:两点之间线段最短.
14.见解析
【解析】如图,作小明关于活动区域边线OP的对称点A′,连接AA′交OP于点B,则小明行走的路线是小明→B→A,即在B处捡球,才能最快拿到球跑到目的地A.
15.第一问:如图沿线段AD爬行;第二问取线段EJ的中点M,连结AM和MI,此路线为蚂蚁爬行的路线.
【解析】解:第一问:如图沿线段AD爬行;
第二问取线段EJ的中点M,连结AM和MI,此路线为蚂蚁爬行的路线.
理由都是:两点之间线段最短.
16.如图①,(1)见解析,理由:两点之间线段最短;(2)见解析.
【解析】(1)如图①,理由:两点之间线段最短.
(2)如图②,这种最短路线有4条.
答案第1页,共2页
答案第1页,共2页
