沪科版数学九年级上册 21.6 综合与实践 获取最大利润课件(共16张PPT)
文档属性
| 名称 | 沪科版数学九年级上册 21.6 综合与实践 获取最大利润课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 201.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-27 00:00:00 | ||
图片预览






文档简介
(共16张PPT)
获取最大利润
综合与实践
2.二次函数y=ax2+bx+c的图象是一条 ,它的对称轴
是 ,顶点坐标是 。当a>0时,抛物线
开口向 ,有最 点,函数有最 值,是 ;当
a<0时,抛物线开口向 ,有最 点,函数有最 值,
是 。
抛物线
旧知回顾
上
小
下
大
高
低
1.二次函数y=a(x-h)2+k的图象是一条 ,它的对称轴是 ,顶点坐标是 。
抛物线
直线x=h
(h,k)
3.二次函数y=2(x-3)2+5的对称轴是 ,顶点坐标是 。当x= 时,y的最 值是 。
4.二次函数y=-3(x+4)2-1的对称轴是 ,顶点坐标是 。当x= 时,函数有最 值,是 。
5.二次函数y=2x2-8x+9的对称轴是 ,顶点
坐标是 。当x= 时,函数有最 值,是 。
直线x=3
(3,5)
3
小
5
直线x=-4
(-4,-1)
-4
大
-1
直线x=2
(2,1)
2
小
1
某大型商场的杨总到T恤衫部去视察,了解的情况如下:已知成批购进时单价是20元。根据市场调查,销售量与销售单价满足如下关系:在一段时间内,单价是35元时,销售量是600件,而单价每降低1元,就可以多销售200件。于是杨总给该部门王经理下达一个任务,马上制定出获利最多的销售方案,这可把王经理给难住了?你能帮他解决这个问题吗?
王经理的困惑:怎样获利更多?
王经理经营T恤衫,购进时单价是20元。市场调查发现:在一段时间内,单价是35元时,销售量是600件;而单价每降低1元,就可以多售出200件。
王经理想知道:
1.价格下降,销量增加,总利润是增加还是减少?
2.降价多少时,可以获得最大利润?
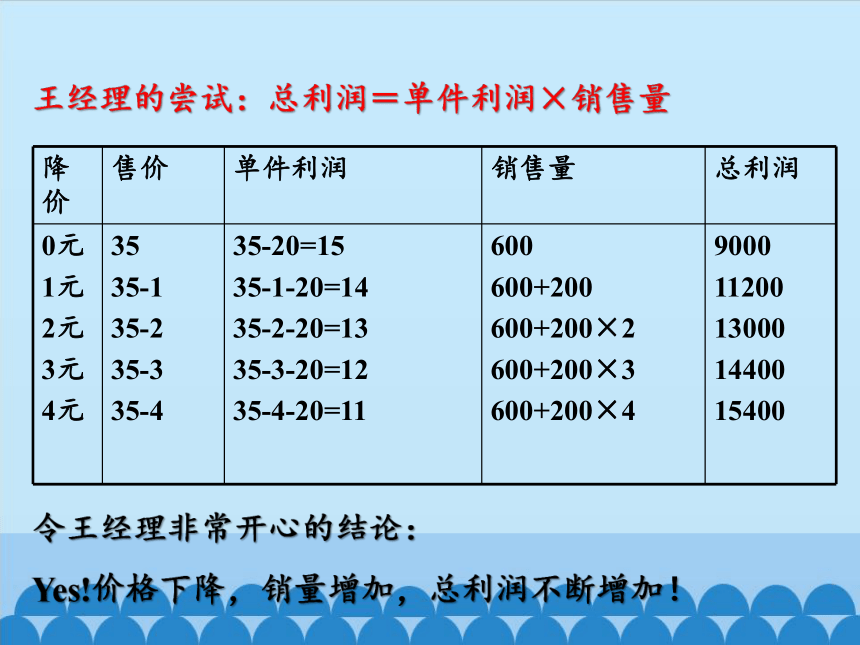
王经理的尝试:总利润=单件利润×销售量
降价 售价 单件利润 销售量 总利润
0元 1元 2元 3元 4元 35 35-1 35-2 35-3 35-4 35-20=15 35-1-20=14 35-2-20=13 35-3-20=12 35-4-20=11 600 600+200 600+200×2 600+200×3 600+200×4 9000
11200
13000
14400
15400
令王经理非常开心的结论:
Yes!价格下降,销量增加,总利润不断增加!
某大型商场经营T恤衫,已知成批购进时单价是20元。根据市场调查,销售量与销售单价满足如下关系:在一段时间内,单价是35元时,销售量是600件,而单价每降低1元,就可以多销售200件。请问:销售单价是多少元时,可以获利最大?最大利润为多少?(单价取整数)
探究
如果设销售单价为x元(20 ≤ x ≤ 35,且 x为整数),获得的利润为y元。
每件降价________元
35-x
销售量可以表示为___________________件
600+200(35-x)
每件利润__________元
x-20
获得的总利润 y=_____________________
(x-20)[600+200(35-x)]
=-200x2+11600x-152000
=-200(x-29)2+16200
探究
y=-200x2+11600x-152000(20≤x≤35,且为整数)
你能画出该函数的图象吗?
=-200(x-29)2+16200
x … 27 28 29 30 31 …
y … 15400 16000 16200 16000 15400 …
O
27
28
29
30
x/元
15400
15600
15800
16000
16200
16400
y/元
31
若要求总利润不低于15400元,那么可以制定哪几种价格?
构建二次函数模型:将问题转化为二次函数的一个具体的表达式。
求二次函数的最大(或最小值)。
运用函数来决策定价的问题:
总结
等量关系:橙子的总产量=每棵橙子树的产量×橙子树的数量
议一议
1.某果园有100棵橙子树,每一棵树平均结600个橙子。现准备多种一些橙子树以提高产量,但是如果多种树,那么树之间的距离和每一棵树所接受的阳光就会减少。根据经验估计,每多种一棵树,平均每棵树就会少结5个橙子。问增种多少棵橙子树,可以使橙子的总产量最多?
y=(100+x)(600-5x)=-5x2+100x+60000=-5(x-10)2+60500
∵a<0 ∴y有最大值
2.利用函数图象描述橙子的总产量y与增种橙子树的棵数x之间的关系。
当x<10时,橙子的总产量随增种棵树的增加而增加;
当x>10时,橙子的总产量随增种棵树的增加而减少。
当x=10时,橙子的总产量最大。
O
5
10
15
20
x/棵
60000
60100
60200
60300
60400
60500
60600
y/个
增种6、7、8、9、10、11、12、13或14棵橙子树,都可以使橙子的总产量在60400个以上。
x1
x2
归纳小结:
运用二次函数的性质求实际问题的最大值和最小值的一般步骤:
1.求出函数解析式和自变量的取值范围;
2.配方变形,或利用公式求它的最大值或最小值;
3.检查求得的最大值或最小值对应的自变量的值必须在自变量的取值范围内。
拓展
某商品现在的售价为每件60元,每星期可卖出300件。市场调查反映:如果调整价格,每涨价1元,每星期要少卖出10件;每降价1元,每星期可多卖出18件,已知商品的进价为每件40元,如何定价才能使利润最大?
分析:调整价格包括涨价和降价两种情况,我们先来看涨价的情况。
y=(60+x)(300-10x)-40(300-10x)
设每件涨价x元,则每星期卖出(300-10x)件,单件商品的利润为(60+x-40)元。
即y=-10x2+100x+6000
怎样确定x的取值范围?
其中,0≤x≤30。
(0≤X≤30)
当x=____时,y最大,也就是说,在涨价的情况下,涨价___元,即定价____元时,利润最大,最大利润为______元。
5
5
65
6250
谢 谢
获取最大利润
综合与实践
2.二次函数y=ax2+bx+c的图象是一条 ,它的对称轴
是 ,顶点坐标是 。当a>0时,抛物线
开口向 ,有最 点,函数有最 值,是 ;当
a<0时,抛物线开口向 ,有最 点,函数有最 值,
是 。
抛物线
旧知回顾
上
小
下
大
高
低
1.二次函数y=a(x-h)2+k的图象是一条 ,它的对称轴是 ,顶点坐标是 。
抛物线
直线x=h
(h,k)
3.二次函数y=2(x-3)2+5的对称轴是 ,顶点坐标是 。当x= 时,y的最 值是 。
4.二次函数y=-3(x+4)2-1的对称轴是 ,顶点坐标是 。当x= 时,函数有最 值,是 。
5.二次函数y=2x2-8x+9的对称轴是 ,顶点
坐标是 。当x= 时,函数有最 值,是 。
直线x=3
(3,5)
3
小
5
直线x=-4
(-4,-1)
-4
大
-1
直线x=2
(2,1)
2
小
1
某大型商场的杨总到T恤衫部去视察,了解的情况如下:已知成批购进时单价是20元。根据市场调查,销售量与销售单价满足如下关系:在一段时间内,单价是35元时,销售量是600件,而单价每降低1元,就可以多销售200件。于是杨总给该部门王经理下达一个任务,马上制定出获利最多的销售方案,这可把王经理给难住了?你能帮他解决这个问题吗?
王经理的困惑:怎样获利更多?
王经理经营T恤衫,购进时单价是20元。市场调查发现:在一段时间内,单价是35元时,销售量是600件;而单价每降低1元,就可以多售出200件。
王经理想知道:
1.价格下降,销量增加,总利润是增加还是减少?
2.降价多少时,可以获得最大利润?
王经理的尝试:总利润=单件利润×销售量
降价 售价 单件利润 销售量 总利润
0元 1元 2元 3元 4元 35 35-1 35-2 35-3 35-4 35-20=15 35-1-20=14 35-2-20=13 35-3-20=12 35-4-20=11 600 600+200 600+200×2 600+200×3 600+200×4 9000
11200
13000
14400
15400
令王经理非常开心的结论:
Yes!价格下降,销量增加,总利润不断增加!
某大型商场经营T恤衫,已知成批购进时单价是20元。根据市场调查,销售量与销售单价满足如下关系:在一段时间内,单价是35元时,销售量是600件,而单价每降低1元,就可以多销售200件。请问:销售单价是多少元时,可以获利最大?最大利润为多少?(单价取整数)
探究
如果设销售单价为x元(20 ≤ x ≤ 35,且 x为整数),获得的利润为y元。
每件降价________元
35-x
销售量可以表示为___________________件
600+200(35-x)
每件利润__________元
x-20
获得的总利润 y=_____________________
(x-20)[600+200(35-x)]
=-200x2+11600x-152000
=-200(x-29)2+16200
探究
y=-200x2+11600x-152000(20≤x≤35,且为整数)
你能画出该函数的图象吗?
=-200(x-29)2+16200
x … 27 28 29 30 31 …
y … 15400 16000 16200 16000 15400 …
O
27
28
29
30
x/元
15400
15600
15800
16000
16200
16400
y/元
31
若要求总利润不低于15400元,那么可以制定哪几种价格?
构建二次函数模型:将问题转化为二次函数的一个具体的表达式。
求二次函数的最大(或最小值)。
运用函数来决策定价的问题:
总结
等量关系:橙子的总产量=每棵橙子树的产量×橙子树的数量
议一议
1.某果园有100棵橙子树,每一棵树平均结600个橙子。现准备多种一些橙子树以提高产量,但是如果多种树,那么树之间的距离和每一棵树所接受的阳光就会减少。根据经验估计,每多种一棵树,平均每棵树就会少结5个橙子。问增种多少棵橙子树,可以使橙子的总产量最多?
y=(100+x)(600-5x)=-5x2+100x+60000=-5(x-10)2+60500
∵a<0 ∴y有最大值
2.利用函数图象描述橙子的总产量y与增种橙子树的棵数x之间的关系。
当x<10时,橙子的总产量随增种棵树的增加而增加;
当x>10时,橙子的总产量随增种棵树的增加而减少。
当x=10时,橙子的总产量最大。
O
5
10
15
20
x/棵
60000
60100
60200
60300
60400
60500
60600
y/个
增种6、7、8、9、10、11、12、13或14棵橙子树,都可以使橙子的总产量在60400个以上。
x1
x2
归纳小结:
运用二次函数的性质求实际问题的最大值和最小值的一般步骤:
1.求出函数解析式和自变量的取值范围;
2.配方变形,或利用公式求它的最大值或最小值;
3.检查求得的最大值或最小值对应的自变量的值必须在自变量的取值范围内。
拓展
某商品现在的售价为每件60元,每星期可卖出300件。市场调查反映:如果调整价格,每涨价1元,每星期要少卖出10件;每降价1元,每星期可多卖出18件,已知商品的进价为每件40元,如何定价才能使利润最大?
分析:调整价格包括涨价和降价两种情况,我们先来看涨价的情况。
y=(60+x)(300-10x)-40(300-10x)
设每件涨价x元,则每星期卖出(300-10x)件,单件商品的利润为(60+x-40)元。
即y=-10x2+100x+6000
怎样确定x的取值范围?
其中,0≤x≤30。
(0≤X≤30)
当x=____时,y最大,也就是说,在涨价的情况下,涨价___元,即定价____元时,利润最大,最大利润为______元。
5
5
65
6250
谢 谢
