沪科版数学九年级上册 22.2 直角三角形相似的判定课件(共15张PPT)
文档属性
| 名称 | 沪科版数学九年级上册 22.2 直角三角形相似的判定课件(共15张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-27 11:54:20 | ||
图片预览




文档简介
(共15张PPT)
B
A
C
A′
B′
C′
复习
问题1 我们学过的三角形相似的判定定理有
哪些?
判定定理3:三边对应成比例,两三角形相似。
判定定理1:两角对应相等,两三角形相似。
判定定理2:两边对应成比例且夹角相等,
两三角形相似。
1.
两条直角边对应成比例的两直角三角形相似。
( )
2.
有一锐角相等的两直角三角形相似。
( )
3.
一直角三角形的三边分别为3,4,5,另一直角三角形的两边分别为6,8,则这两个直角三角形相似。
( )
√
√
×
判断题
判定:
已知:RtΔABC和RtΔA'B'C'中,∠C=∠C'=90°.依据下列各组条件判定这两个三角形是不是相似,并说明为什么:
(1) ∠A=25°,∠B'=65°;
(2) AC=3,BC=4,A'C'=6,B'C'=8;
(3) AB=10,AC=8,A'B'=15,B'C'=9.
已知:如图RtΔABC与RtΔA′B′C′中,
∠C=∠C’=90°,
求证: RtΔABC ∽ RtΔA'B'C'
定理证明:
A
B
C
A'
B'
C'
证明一
A
C
A'
B'
C'
ΔABC∽ΔA'B'C‘
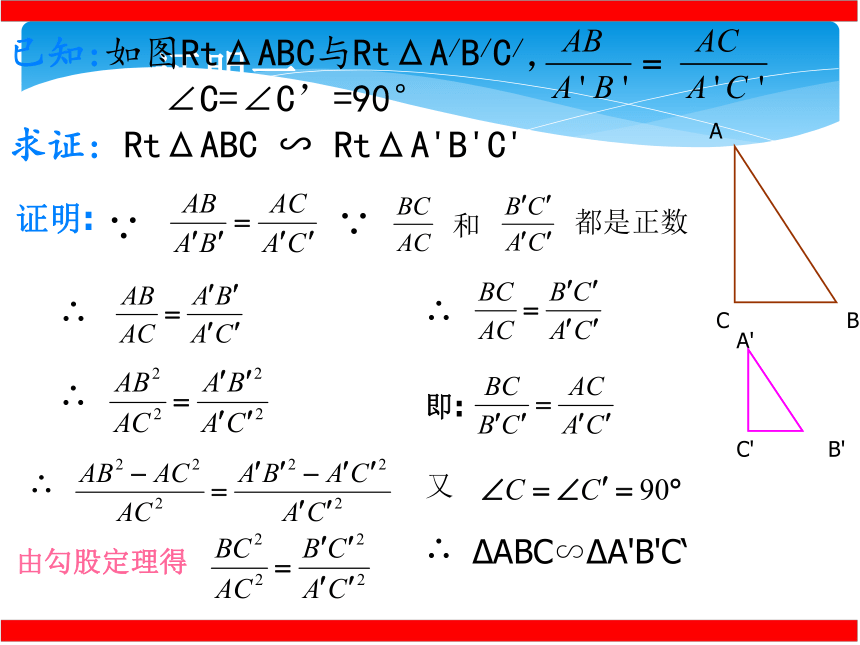
由勾股定理得
和
都是正数
即:
又
证明:
B
已知:如图RtΔABC与RtΔA/B/C/,
∠C=∠C’=90°
求证: RtΔABC ∽ RtΔA'B'C'
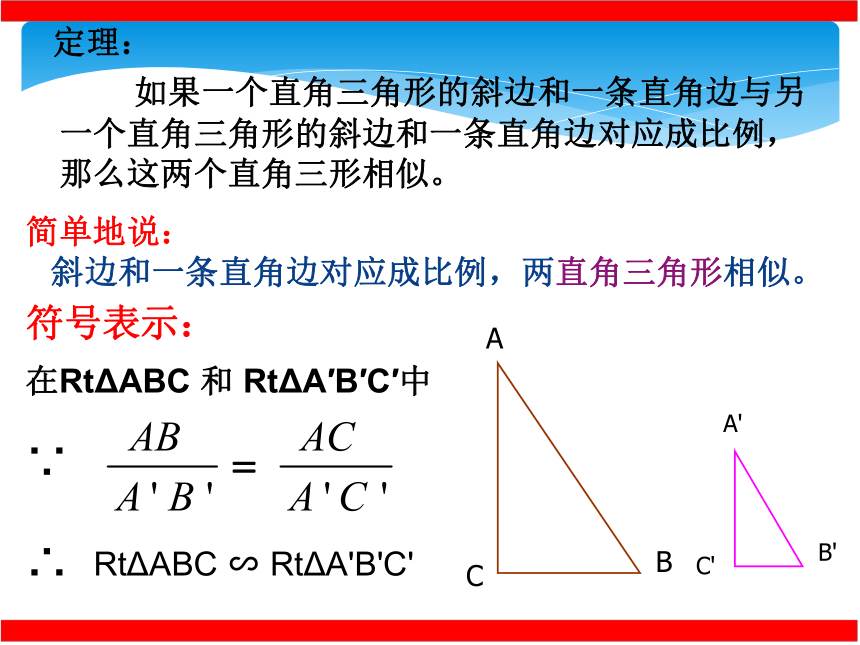
如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三形相似。
简单地说:
斜边和一条直角边对应成比例,两直角三角形相似。
定理:
A
B
C
A'
B'
C'
符号表示:
∵
∴
RtΔABC ∽ RtΔA'B'C'
在RtΔABC 和 RtΔA′B′C′中
△ABC为锐角三角形,BD、CE为高 .
求证:△ ADE∽ △ ABC
证明:
∵BD⊥AC,CE⊥AB
1
A
B
C
D
E
例题1:
∴∠ABD+∠A=90°,∠ACE+∠A= 90°
∴ ∠ABD= ∠ACE
又∵ ∠A= ∠A
∴△ ABD ∽ △ ACE
∴
∵ ∠A= ∠A ∴ △ ADE ∽ △ ABC
例题2:
已知:如图,CE交△ABC的高线AD于点O,交AB于E
且
求证:
A
D
B
C
O
E
解:
ΔABC∽ΔCDB
A
C
B
b
a
D
例3:如图,已知∠ABC=∠CDB=90°,AC=b,BC=a, 当BD与a,b之间满足怎样的关系时,ΔABC∽ΔCDB
答:
当
时,
ΔABC∽ΔCDB
ΔABC∽ΔCDB
即
时,
1.在ΔABC与 ΔBCD中,已知∠ABC=∠CDB=90°,AC=a,BC=b, 当BD与a,b之间满足怎样的关系时,有两个三角形相似?
A
B
D
C
a
b
分析:
如图(1):当AC与CB,BC与DB对应
RtΔABC∽RtΔCDB,由上例知
图(1)
ΔABC∽ΔBDC,
如图(2):
ΔABC∽ΔBDC,
答:
当
或
有两个三角形相似
A
B
C
D
a
提示:对条件探索性问题,在解题时应分类对每一种情况进行讨论,切不可凭主观想象,只解一种情况,而忽略其他的解。
b
图(2)
2.如图,在RtΔABC中,CD是斜边AB上的高,E是BC上的一点,AE交CD于点F,AE AD=AF AC,
求证:(1) AE是∠CAB的平分线;
(2) AB AF=AC AE。
A
B
C
D
E
F
分析:
要证明AE是∠CAB的平分线,只要证明RtΔACE∽RtΔADF即可
要证明 AB AF=AC AE,
只要证明 ΔACF∽ΔABE
课堂小结:
2.直角三角形相似的判定除了本节定理外,前面判定任意三角形相似的方法对直角三角形同样适用。
3.关于探索性题目的处理,要考虑各种可能的 情况。
1.如果一个直角三角形的斜边和一条直角边与另一个直角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似。
作业:教材P84 练习 1,2,3.
教材P85 习题22.2 10,11.
课后思考:
B
A
C
A′
B′
C′
复习
问题1 我们学过的三角形相似的判定定理有
哪些?
判定定理3:三边对应成比例,两三角形相似。
判定定理1:两角对应相等,两三角形相似。
判定定理2:两边对应成比例且夹角相等,
两三角形相似。
1.
两条直角边对应成比例的两直角三角形相似。
( )
2.
有一锐角相等的两直角三角形相似。
( )
3.
一直角三角形的三边分别为3,4,5,另一直角三角形的两边分别为6,8,则这两个直角三角形相似。
( )
√
√
×
判断题
判定:
已知:RtΔABC和RtΔA'B'C'中,∠C=∠C'=90°.依据下列各组条件判定这两个三角形是不是相似,并说明为什么:
(1) ∠A=25°,∠B'=65°;
(2) AC=3,BC=4,A'C'=6,B'C'=8;
(3) AB=10,AC=8,A'B'=15,B'C'=9.
已知:如图RtΔABC与RtΔA′B′C′中,
∠C=∠C’=90°,
求证: RtΔABC ∽ RtΔA'B'C'
定理证明:
A
B
C
A'
B'
C'
证明一
A
C
A'
B'
C'
ΔABC∽ΔA'B'C‘
由勾股定理得
和
都是正数
即:
又
证明:
B
已知:如图RtΔABC与RtΔA/B/C/,
∠C=∠C’=90°
求证: RtΔABC ∽ RtΔA'B'C'
如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三形相似。
简单地说:
斜边和一条直角边对应成比例,两直角三角形相似。
定理:
A
B
C
A'
B'
C'
符号表示:
∵
∴
RtΔABC ∽ RtΔA'B'C'
在RtΔABC 和 RtΔA′B′C′中
△ABC为锐角三角形,BD、CE为高 .
求证:△ ADE∽ △ ABC
证明:
∵BD⊥AC,CE⊥AB
1
A
B
C
D
E
例题1:
∴∠ABD+∠A=90°,∠ACE+∠A= 90°
∴ ∠ABD= ∠ACE
又∵ ∠A= ∠A
∴△ ABD ∽ △ ACE
∴
∵ ∠A= ∠A ∴ △ ADE ∽ △ ABC
例题2:
已知:如图,CE交△ABC的高线AD于点O,交AB于E
且
求证:
A
D
B
C
O
E
解:
ΔABC∽ΔCDB
A
C
B
b
a
D
例3:如图,已知∠ABC=∠CDB=90°,AC=b,BC=a, 当BD与a,b之间满足怎样的关系时,ΔABC∽ΔCDB
答:
当
时,
ΔABC∽ΔCDB
ΔABC∽ΔCDB
即
时,
1.在ΔABC与 ΔBCD中,已知∠ABC=∠CDB=90°,AC=a,BC=b, 当BD与a,b之间满足怎样的关系时,有两个三角形相似?
A
B
D
C
a
b
分析:
如图(1):当AC与CB,BC与DB对应
RtΔABC∽RtΔCDB,由上例知
图(1)
ΔABC∽ΔBDC,
如图(2):
ΔABC∽ΔBDC,
答:
当
或
有两个三角形相似
A
B
C
D
a
提示:对条件探索性问题,在解题时应分类对每一种情况进行讨论,切不可凭主观想象,只解一种情况,而忽略其他的解。
b
图(2)
2.如图,在RtΔABC中,CD是斜边AB上的高,E是BC上的一点,AE交CD于点F,AE AD=AF AC,
求证:(1) AE是∠CAB的平分线;
(2) AB AF=AC AE。
A
B
C
D
E
F
分析:
要证明AE是∠CAB的平分线,只要证明RtΔACE∽RtΔADF即可
要证明 AB AF=AC AE,
只要证明 ΔACF∽ΔABE
课堂小结:
2.直角三角形相似的判定除了本节定理外,前面判定任意三角形相似的方法对直角三角形同样适用。
3.关于探索性题目的处理,要考虑各种可能的 情况。
1.如果一个直角三角形的斜边和一条直角边与另一个直角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似。
作业:教材P84 练习 1,2,3.
教材P85 习题22.2 10,11.
课后思考:
